Grid-Based Path-Finding
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

View the Manual
A Important Health Warning: Photosensitive Seizures A very small percentage of people may experience a seizure when exposed to certain visual images, including flashing lights or patterns that may appear in video games. Even people with no history of seizures or epilepsy may have an undiagnosed condition that can cause “photosensitive epileptic seizures” while watching video games. Symptoms can include light-headedness, altered vision, eye or face twitching, jerking or shaking of arms or legs, disorientation, confusion, momentary loss of awareness, and loss of consciousness or convulsions that can lead to injury from falling down or striking nearby objects. Immediately stop playing and consult a doctor if you experience any of these symptoms. Parents, watch for or ask children about these symptoms—children and teenagers are more likely to experience these seizures. The risk may be reduced by being farther from the screen; using a smaller screen; playing in a well-lit room, and not playing when drowsy or fatigued. If you or any relatives have a history of seizures or epilepsy, consult a doctor before playing. © 2019 The Codemasters Software Company Limited (“Codemasters”). All rights reserved. “Codemasters”®, “EGO”®, the Codemasters logo and “Grid”® are registered trademarks owned by Codemasters. “RaceNet”™ is a trademark of Codemasters. All rights reserved. Uses Bink Video. Copyright © 1997-2019 by RAD Game Tools, Inc. Powered by Wwise © 2006 - 2019 Audiokinetic Inc. All rights reserved. Ogg Vorbis Libraries © 2019, Xiph.Org Foundation. Portions of this software are copyright ©2019 The FreeType Project (www.freetype.org). All rights reserved. All other copyrights or trademarks are the property of their respective owners and are being used under license. -
Grid 2 Ps3 Cheat Codes Grid 2 Ps3 Cheat Codes
grid 2 ps3 cheat codes Grid 2 ps3 cheat codes. Completing the CAPTCHA proves you are a human and gives you temporary access to the web property. What can I do to prevent this in the future? If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware. If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices. Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store. Cloudflare Ray ID: 6651d062fee215f8 • Your IP : 188.246.226.140 • Performance & security by Cloudflare. GRID cheats & more for PlayStation 3 (PS3) Get the latest GRID cheats, codes, unlockables, hints, Easter eggs, glitches, tips, tricks, hacks, downloads, trophies, guides, FAQs, walkthroughs, and more for PlayStation 3 (PS3). CheatCodes.com has all you need to win every game you play! Use the above links or scroll down see all to the PlayStation 3 cheats we have available for GRID. Genre: Racing, Sports Car Auto Racing Developer: Codemasters Publisher: Codemasters ESRB Rating: Everyone Release Date: June 30, 2008. Hints. We have no tips for GRID yet. If you have any unlockables please submit them. GRID 2 Walkthrough. The race returns in the highly-anticipated sequel to the critically acclaimed, BAFTA award-winning Race Driver: GRID which set new standards for damage, AI, visuals and introduced Flashback, the time rewind feature now adopted by many racing titles. -

Annual Report & Accounts 2020
DRIVEN BY AMBITION ANNUAL REPORT & ACCOUNTS 2020 w FOR OVER 30 YEARS CODEMASTERS HAS BEEN PUSHING BOUNDARIES 2020 WAS NO DIFFERENT. WE’VE ONLY JUST STARTED. STRATEGIC REPORT Our Highlights 02 Company Overview 02 Chairman’s Statement 04 Market Overview 06 Chief Executive’s Review 10 Our Strategy 14 Strategy in Action 16 12 Months at Codemasters 18 DiRT Rally 2.0 24 F1 2019 26 F1 Mobile Racing 28 GRID 29 Financial Review 30 Principal Risks and Mitigations 34 GOVERNANCE Board of Directors 36 Corporate Governance Statement 38 Audit Committee Report 42 Remuneration Committee Report 44 Directors’ Report 47 Statement of Directors Responsibilities 48 Independent Auditor’s Report to the Members of Codemasters Group Holdings plc 49 Codemasters produces FINANCIAL STATEMENTS iconic games and is a world leader in the Consolidated Income Statement 56 Consolidated Statement of Comprehensive Income 57 development and Statement of Changes in Equity 58 publishing of racing titles. Consolidated Statement of Financial Position 59 Consolidated Cash Flow Statement 60 Notes to the Consolidated Financial Statements 61 Company Statement of Financial Position 96 Company Statement of Changes in Equity 97 Notes to the Company Financial Statements 98 Company Information 102 S trategic R eport G IN POLE POSITION overnance Codemasters is a world-leader in the F inancial development and publishing of racing games across console, PC, streaming, S and mobile. It is the home of revered tatements franchises including DiRT, GRID and the F1® series of videogames. In November 2019, the Group acquired Slightly Mad Studios and added the award-winning Project CARS franchise to its portfolio alongside Fast & Furious Crossroads. -

Race Driver: GRID: EVALUATION SUMMARY
Race Driver: GRID: EVALUATION SUMMARY About Race INDIVIDUAL SCORES RYG’s RATING* Driver: GRID Developed and published by Codemasters, Race Driver: 48% GRID is a racing-simulation game and forms a part of the TOCA Touring Car Series. Many critics praised GRID for its realism, particularly on car damages. This version of DiRT was bundled within a Racing Megapack distributed UNACCEPTABLE by Codemasters. 44% 52% N/A Medium: Disc Version Versions Tested: 1.00 and 1.30 * RYG’s Rating is an aggregate of the Individual Scores AREAS OF CONCERN About SecuROM Pre-Purchase & DRM Notification Activation DRM: SecuROM documentation absent from Publisher’s DRM: Hardware activation; Disc required to play GRID; Resale SecuROM is developed by Sony DADC and remains one websites, Gaming Package, Manual, Readme and EULA. prohibited. of the oldest DRM series in the Video Gaming market. Publisher: As above. Publisher: As above. This version implemented by Codemasters is a hardware- based DRM with blacklisting capabilities. EULA Manual Game Patches & Updates DRM: EULA absent from Sony DADC. DRM: No notification of DRM upgrade. About Publisher: As above; Written based on UK laws; Publisher: As above; No EULA provided; Cannot roll back to Incomprehensible and inconsistent; No warranties/refunds previous version if errors arise. Codemasters provisions for consumers outside UK; Ownership bias; Internal Disputes Resolution non-existent. Uninstallation DRM: DRM Removal tool not provided in game; Many files Codemasters Software Company Limited is a UK-based Personal Backup and registry keys remain. video games developer and publisher overseeing about BOTH: Not permissible as per EULA and DRM implemented. -

Samsung Lanserer Gamefly Streaming – Fremtidens Videospill
18-08-2015 17:14 CEST Samsung lanserer GameFly Streaming – fremtidens videospill Oslo18. august, 2015 – Samsung Electronics Co. Ltd. presenterer fremtidens high-end videospill med lanseringen av GameFly Streaming, en abonnementsbasert tjeneste som bringer nyskapende spill inn i folks stuer, uten behov for konsoller, kabler eller plater. GameFly Streaming strømmer populære spill som Batman Arkham Origins, Lego Batman 3, GRID 2 og HITMAN Absolution over internett, slik at de kan spilles direkte på Samsungs Smart TV-er. Den patenterte GameFly-teknologien integreres i Samsung Smart TV-er for å sikre en pålitelig og responsiv opplevelse, selv om nettverksforholdene varierer under en spilløkt. – GameFly Streaming er virkelig en game-changer, sier Marko Nurmela, visepresident for marked og kommunikasjon i Samsung. Ved å opprette et abonnement kan alle fra nybegynnere til seriøse spillere gjøre om sin Samsung Smart TV til neste generasjons spillkonsoll. Det er på tide å si farvel til alle bokser, ledninger og DVD-er som hoper seg opp i stuen. Med GameFly trenger du kun en kompatibel Samsung Smart TV og en spillkontroll for å nyte den beste spillopplevelsen. Det er flere ulike spillpakker tilgjengelig for GameFly Streaming-kundene; ´Hardcore-pakken` med spill som Mafia 2 og Red Faction, ´Lego-pakken` med titlene Batman (1,2 og 3) og Lord of the Rings, samt en ´All Around-pakke`. Månedlig abonnement koster 69,99 kroner for Hardcore-pakken, 69,99 kroner for Lego-pakken og 59,99 for All Around-pakken. Fakta: Kompatible TV-er • 2015 Smart TV-er (J5500 og nyere) • 2014 Smart TV-er (H5500 og nyere) Anbefalte spillkontroller • Logitech F310, F710 • Xbox 360 kontroll med ledning Krav til tilkobling • Internett-båndbredde • 8Mbps for HD streaming • 4Mbps for SD streaming. -

Metadefender Core V4.17.3
MetaDefender Core v4.17.3 © 2020 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 13 Key Features of MetaDefender Core 14 1. Quick Start with MetaDefender Core 15 1.1. Installation 15 Operating system invariant initial steps 15 Basic setup 16 1.1.1. Configuration wizard 16 1.2. License Activation 21 1.3. Process Files with MetaDefender Core 21 2. Installing or Upgrading MetaDefender Core 22 2.1. Recommended System Configuration 22 Microsoft Windows Deployments 22 Unix Based Deployments 24 Data Retention 26 Custom Engines 27 Browser Requirements for the Metadefender Core Management Console 27 2.2. Installing MetaDefender 27 Installation 27 Installation notes 27 2.2.1. Installing Metadefender Core using command line 28 2.2.2. Installing Metadefender Core using the Install Wizard 31 2.3. Upgrading MetaDefender Core 31 Upgrading from MetaDefender Core 3.x 31 Upgrading from MetaDefender Core 4.x 31 2.4. MetaDefender Core Licensing 32 2.4.1. Activating Metadefender Licenses 32 2.4.2. Checking Your Metadefender Core License 37 2.5. Performance and Load Estimation 38 What to know before reading the results: Some factors that affect performance 38 How test results are calculated 39 Test Reports 39 Performance Report - Multi-Scanning On Linux 39 Performance Report - Multi-Scanning On Windows 43 2.6. Special installation options 46 Use RAMDISK for the tempdirectory 46 3. -

Overview (October 2011) Our Legacy
“WORLD OF MASS DEVELOPMENT” OVERVIEW (OCTOBER 2011) OUR LEGACY 2005 2011 NOW • Core team from Simbin formed BlimeyGames and then Slightly Mad Studios • Now a 65+ worldwide company • #17 “Develop Top 100 Studios” • Central studio located near Tower Bridge, London • Sister company GAMAGIO focusing on social/mobile games and technology KEY STRENGTHS 8 years experience Distributed development • Each title rated 84+ Metacritic • Ultra-efficient (less production time than a traditional studio) • AAA development for Electronic Arts • Cost-effective • SHIFT franchise has sold 6m+ copies • Attracts worldwide talent • Proven track record delivering within time & budget • Key staff based in the UK • Well-known developer with strong industry links KEY STRENGTHS Full ownership of all tech... • Cross-platform MADNESS engine (HDR, per- pixel, volumetric, radiosity, anisotropic light mapping) • Proprietary AI and Physics • Multi-core/multi-processor architecture • Modular scalable support for different game genres OUR NEW VENTURE... INTRODUCING WORLD OF MASS DEVELOPMENT CREATED BY YOU. WHAT IS WMD? “A platform for games projects that are funded by the community” OR... A NEW WAY TO AAA “WMD transforms the way games are created... By connecting the creators with the players rather than the publishers, traditional overheads and a focus on release windows/financial quarters/ marketing etc.. shifts back to concentrating on making great games that people want to play whilst still getting proper QA and funding.” - IAN BELL, STUDIO HEAD (SLIGHTLY MAD STUDIOS) -

Dragon Magazine #220
Issue #220 SPECIAL ATTRACTIONS Vol. XX, No. 3 August 1995 Stratagems and Dirty Tricks Gregory W. Detwiler 10 Learn from the masters of deception: advice for DMs Publisher and players. TSR, Inc. The Politics of Empire Colin McComb & Associate Publisher 16 Carrie Bebris Brian Thomsen Put not your faith in the princes of this Editor world achieve victory in the BIRTHRIGHT Wolfgang Baur campaign through superior scheming. Associate editor Dave Gross Hired Killerz Ed Stark 22 Meet Vlad Taltos, and see how assassins can play a Fiction editor crucial role in any RPG. Barbara G. Young Art director FICTION Larry W. Smith Hunts End Rudy Thauberger Editorial assistant 98 One halfling and two thri-kreen reach the end of the road. Michelle Vuckovich Production staff Tracey Isler REVIEWS Role-playing Reviews Lester Smith Subscriptions 48 Lester examines PSYCHOSIS: Ship of Fools* and other Janet L. Winters terrifying RPGs. U. s. advertising Eye of the Monitor David Zeb Cook, Paul Murphy, and Cindy Rick 63 Ken Rolston U.K. correspondent BLOOD BOWL* goes electronic, the computer plots against and U.K. advertising you in Microproses Machiavelli, and we take another look Carolyn Wildman at Warcraft. From the Forge Ken Carpenter 128 Whatever happened to quality painting? A few words about neon paint jobs. DRAGON® Magazine (ISSN 1062-2101) is published Magazine Marketing, Tavistock Road, West Drayton, monthly by TSR, inc., 201 Sheridan Springs Road, Middlesex UB7 7QE, United Kingdom; telephone: Lake Geneva WI 53147, United States of America. The 0895-444055. postal address for all materials from the United States Subscriptions: Subscription rates via second-class of America and Canada except subscription orders is: mail are as follows: $30 in U.S. -

GEM Box Gaming-Entertainment-Multimedia
GEM Box Gaming-Entertainment-Multimedia www.emtec-gembox.com Un mondo di divertimento in un piccolo TV box . Una console per tutta la famiglia . Un autentico hub multimediale . Accedi ai giochi Android da Google Play . Naviga in Internet e su YouTube. direttamente sul grande schermo. Guarda foto, video e ascolta musica. Gioca in streaming a più di 100 grandi titoli in qualità console tramite GameFly Streaming. Funzione Miracast. Accedi alla tua collezione di giochi su PC dal TV di casa. Interfaccia semplice e intuitiva . Riscopri giochi retro grazie a una selezione di emulatori. Giochi Android 4 fantastici giochi precaricati! • Appena configurato il tuo GEM Box, potrai immediatamente giocare ai 4 titoli Gameloft precaricati! • La selezione di giochi è perfetta per accontentare i gusti di tutti i membri della famiglia! Asphalt 8: Airborne GT Racing 2 Wonder Zoo My Little Pony Divertiti con i tuoi giochi Android preferiti • Scarica i tuoi giochi preferiti da Google Play • GEM Store - Una selezione di 150 grandi titoli, tutti giocabili con il GEM Pad - I giochi sono ordinati per categoria - La maggior parte dei giochi è gratuita! Beach Dungeon Clarc Soulcraft World at Desplicable Shadow Cordy 2 Meganoid Red Bull Dead Buggy Hunter 4 Arms Me Blade 2 Air Race Trigger Racing Flight Aces of Drift Mania Dungeon The Gungslugs Sword of Double Farm Hero Real Theory the Championship Quest Walking Free Xolan Dragon Invasion Panda Football HD Luftwaffe 2 Dead Trilogy Bomber 2013 GameFly Streaming Un'autentica console di gioco! Goditi giochi di qualità console grazie alla partnership su abbonamento tra GEM Box e GameFly. -

“Forza Horizon” Fact Sheet May 2012
“Forza Horizon” Fact Sheet May 2012 Title: “Forza Horizon” Availability: Oct. 23, 2012, in North America, South America and Asia Oct. 26, 2012, in Europe Publisher: Turn 10 Studios-Microsoft Studios Developer: Playground Games Format: DVD for the Xbox 360 video game and entertainment system; Xbox LIVE- enabled*; better with Kinect PEGI Rating: Pending Pricing: Standard Edition: 69.99 euros estimated retail price** Product Overview: “Forza Horizon” combines legendary “Forza Motorsport” authenticity with a festival atmosphere and the freedom of the open road. Launching this October on Xbox 360, “Forza Horizon” offers an immersive pick-up-and-play open-road racing experience and features the unrivaled realism, diversity and innovation that are hallmarks of the “Forza Motorsport” franchise. Features: Top features include the following: Expansive open road. Take your dream car off the track and onto the open road to race and explore the epic driving landscape of Colorado. Experience a 24-hour dynamic lighting cycle that includes night racing, a first for the “Forza Motorsport” franchise on Xbox 360. “Forza Horizon” brings another first to “Forza Motorsport” with the debut of mixed surface and dirt racing. From stunning mountain highways to dusty back roads, the world of “Forza Motorsport” is bigger and more diverse than ever. This is action racing. “Forza Horizon” combines the legendary “Forza Motorsport” authenticity you know and love with new action-based driving gameplay, rewarding you for your speed, skill and style behind the wheel. Drive the world’s most iconic cars as you compete in festival events, race for pink slips in white-knuckle street races, or just show off your skills to increase your popularity rank. -

Overview (February 2012)
“WORLD OF MASS DEVELOPMENT” OVERVIEW (FEBRUARY 2012) 1 OUR TITLES 84% 90% 10M+ 84% 85% COMING COMMUNITY- SOCIAL/MOBILE METACRITIC METACRITIC DOWNLOADS METACRITIC METACRITIC SOON POWERED TITLES 6M+ SALES 2005 RACING SIM 2012 2 NOW • Core team from Simbin formed BlimeyGames and then Slightly Mad Studios • Now a 65+ worldwide company with central studio located near Tower Bridge, London • SLIGHTLY MAD STUDIOS concentrating on AAA console/PC titles with releases in 2012 • GAMAGIO division focusing on social/mobile and releasing multiple titles & technology in 2011/2012 • WORLD OF MASS DEVELOPMENT platform created to allow community-funded projects 3 KEY STRENGTHS 8 years experience Distributed development • Each title rated 84+ Metacritic • Ultra-efficient (less production time than a traditional studio) • AAA development for Electronic Arts • Cost-effective • Need For Speed SHIFT franchise has sold 6m+ copies • Attracts worldwide talent • Proven track record delivering within time • Key staff based in the UK & budget Full ownership of all tech... • Well-known developer with strong industry links 4 Cross-platform MADNESS engine... • Supports PC, PlayStation 3, XBox 360, Wii U • Supports HDR, per-pixel, volumetric, radiosity, anisotropic light mapping • Proprietary AI and Physics • Multi-core/multi-processor architecture • Modular scalable support for different game genres • “Project CARS” title currently in development for multiple platforms... 5 OUR NEW VENTURE... 6 INTRODUCING WORLD OF MASS DEVELOPMENT CREATED BY YOU. 7 WHAT IS WMD? “A platform for games projects that are funded by the community” OR... A NEW WAY TO AAA “WMD transforms the way games are created... By connecting the creators with the players rather than the publishers, traditional overheads and a focus on release windows/financial quarters/ marketing etc. -
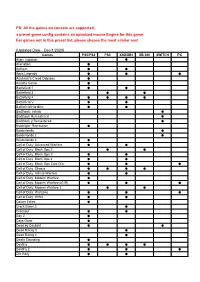
The Games on Console Are Supported, a Preset Game Config Contains an Optmized Mouse Engine for This Game
PS: All the games on console are supported, a preset game config contains an optmized mouse Engine for this game. For games not in this preset list, please choose the most similar one! (Updated Date:Dec/1/2020) Games PS5/PS4 PS3 XSX/XB1 XB 360 SWITCH PC Alien: Isolation ● Alienation ● Anthem ● ● Apex Legends ● ● ● Assassin's Creed Odyssey ● Assetto Corsa ● Battlefield 1 ● ● Battlefield 3 ● ● Battlefield 4 ● ● ● ● Battlefield V ● ● Battlefield Hardline ● ● BioShock: Infinite ● BioShock Remastered ● BioShock 2 Remastered ● Blacklight: Retribution ● Borderlands ● Borderlands 2 ● Borderlands 3 ● Call of Duty: Advanced Warfare ● ● Call of Duty: Black Ops 2 ● ● Call of Duty: Black Ops 3 ● ● Call of Duty: Black Ops 4 ● ● Call of Duty: Black Ops Cold War ● ● ● Call of Duty: Ghosts ● ● ● ● Call of Duty: Infinite Warfare ● ● Call of Duty: Modern Warfare ● Call of Duty: Modern Warfare(2019) ● ● ● Call of Duty: Modern Warfare 3 ● ● Call of Duty: Warzone ● ● ● Call of Duty: WWII ● ● Conan Exiles ● Crack Down 3 ● Crossout ● ● Day Z ● Days Gone ● Dead by Daylight ● ● Dead Rising 3 ● Dead Rising 4 ● Death Stranding ● Destiny ● ● ● ● Destiny 2 ● ● ● Dirt Rally ● ● DIRT 4 ● DJMax Respect ● Doom ● ● ● Doom: Eternal ● DriveClub ● Dying Light ● ● Evolve ● ● F1 2015~2020 ● Fallout 4 ● ● Far Cry 3 ● Far Cry 4 ● Far Cry 5 ● ● Far Cry Primal ● ● For Honor ● Fortnite: Battle Royale ● ● ● Forza 5~7 ● Forza Horizon 2~4 ● Gears of War 3 ● Gears of War 4 ● Gears of War 5 ● Gears of War: Ultimate Edition ● Ghost Recon: Rreakpoint ● Ghost Recon: Wildlands ● ● Grand Theft