Table of Fourier Transform Pairs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

FOURIER TRANSFORM Very Broadly Speaking, the Fourier Transform Is a Systematic Way to Decompose “Generic” Functions Into
FOURIER TRANSFORM TERENCE TAO Very broadly speaking, the Fourier transform is a systematic way to decompose “generic” functions into a superposition of “symmetric” functions. These symmetric functions are usually quite explicit (such as a trigonometric function sin(nx) or cos(nx)), and are often associated with physical concepts such as frequency or energy. What “symmetric” means here will be left vague, but it will usually be associated with some sort of group G, which is usually (though not always) abelian. Indeed, the Fourier transform is a fundamental tool in the study of groups (and more precisely in the representation theory of groups, which roughly speaking describes how a group can define a notion of symmetry). The Fourier transform is also related to topics in linear algebra, such as the representation of a vector as linear combinations of an orthonormal basis, or as linear combinations of eigenvectors of a matrix (or a linear operator). To give a very simple prototype of the Fourier transform, consider a real-valued function f : R → R. Recall that such a function f(x) is even if f(−x) = f(x) for all x ∈ R, and is odd if f(−x) = −f(x) for all x ∈ R. A typical function f, such as f(x) = x3 + 3x2 + 3x + 1, will be neither even nor odd. However, one can always write f as the superposition f = fe + fo of an even function fe and an odd function fo by the formulae f(x) + f(−x) f(x) − f(−x) f (x) := ; f (x) := . e 2 o 2 3 2 2 3 For instance, if f(x) = x + 3x + 3x + 1, then fe(x) = 3x + 1 and fo(x) = x + 3x. -

An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms
An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms Notes prepared for MA3139 Arthur L. Schoenstadt Department of Applied Mathematics Naval Postgraduate School Code MA/Zh Monterey, California 93943 August 18, 2005 c 1992 - Professor Arthur L. Schoenstadt 1 Contents 1 Infinite Sequences, Infinite Series and Improper Integrals 1 1.1Introduction.................................... 1 1.2FunctionsandSequences............................. 2 1.3Limits....................................... 5 1.4TheOrderNotation................................ 8 1.5 Infinite Series . ................................ 11 1.6ConvergenceTests................................ 13 1.7ErrorEstimates.................................. 15 1.8SequencesofFunctions.............................. 18 2 Fourier Series 25 2.1Introduction.................................... 25 2.2DerivationoftheFourierSeriesCoefficients.................. 26 2.3OddandEvenFunctions............................. 35 2.4ConvergencePropertiesofFourierSeries.................... 40 2.5InterpretationoftheFourierCoefficients.................... 48 2.6TheComplexFormoftheFourierSeries.................... 53 2.7FourierSeriesandOrdinaryDifferentialEquations............... 56 2.8FourierSeriesandDigitalDataTransmission.................. 60 3 The One-Dimensional Wave Equation 70 3.1Introduction.................................... 70 3.2TheOne-DimensionalWaveEquation...................... 70 3.3 Boundary Conditions ............................... 76 3.4InitialConditions................................ -

Fourier Transforms & the Convolution Theorem
Convolution, Correlation, & Fourier Transforms James R. Graham 11/25/2009 Introduction • A large class of signal processing techniques fall under the category of Fourier transform methods – These methods fall into two broad categories • Efficient method for accomplishing common data manipulations • Problems related to the Fourier transform or the power spectrum Time & Frequency Domains • A physical process can be described in two ways – In the time domain, by h as a function of time t, that is h(t), -∞ < t < ∞ – In the frequency domain, by H that gives its amplitude and phase as a function of frequency f, that is H(f), with -∞ < f < ∞ • In general h and H are complex numbers • It is useful to think of h(t) and H(f) as two different representations of the same function – One goes back and forth between these two representations by Fourier transforms Fourier Transforms ∞ H( f )= ∫ h(t)e−2πift dt −∞ ∞ h(t)= ∫ H ( f )e2πift df −∞ • If t is measured in seconds, then f is in cycles per second or Hz • Other units – E.g, if h=h(x) and x is in meters, then H is a function of spatial frequency measured in cycles per meter Fourier Transforms • The Fourier transform is a linear operator – The transform of the sum of two functions is the sum of the transforms h12 = h1 + h2 ∞ H ( f ) h e−2πift dt 12 = ∫ 12 −∞ ∞ ∞ ∞ h h e−2πift dt h e−2πift dt h e−2πift dt = ∫ ( 1 + 2 ) = ∫ 1 + ∫ 2 −∞ −∞ −∞ = H1 + H 2 Fourier Transforms • h(t) may have some special properties – Real, imaginary – Even: h(t) = h(-t) – Odd: h(t) = -h(-t) • In the frequency domain these -

STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS and INTERPRETATIONS by DSG Pollock
STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS AND INTERPRETATIONS by D.S.G. Pollock (University of Leicester) Email: stephen [email protected] This paper expounds some of the results of Fourier theory that are es- sential to the statistical analysis of time series. It employs the algebra of circulant matrices to expose the structure of the discrete Fourier transform and to elucidate the filtering operations that may be applied to finite data sequences. An ideal filter with a gain of unity throughout the pass band and a gain of zero throughout the stop band is commonly regarded as incapable of being realised in finite samples. It is shown here that, to the contrary, such a filter can be realised both in the time domain and in the frequency domain. The algebra of circulant matrices is also helpful in revealing the nature of statistical processes that are band limited in the frequency domain. In order to apply the conventional techniques of autoregressive moving-average modelling, the data generated by such processes must be subjected to anti- aliasing filtering and sub sampling. These techniques are also described. It is argued that band-limited processes are more prevalent in statis- tical and econometric time series than is commonly recognised. 1 D.S.G. POLLOCK: Statistical Fourier Analysis 1. Introduction Statistical Fourier analysis is an important part of modern time-series analysis, yet it frequently poses an impediment that prevents a full understanding of temporal stochastic processes and of the manipulations to which their data are amenable. This paper provides a survey of the theory that is not overburdened by inessential complications, and it addresses some enduring misapprehensions. -

Fourier Transform, Convolution Theorem, and Linear Dynamical Systems April 28, 2016
Mathematical Tools for Neuroscience (NEU 314) Princeton University, Spring 2016 Jonathan Pillow Lecture 23: Fourier Transform, Convolution Theorem, and Linear Dynamical Systems April 28, 2016. Discrete Fourier Transform (DFT) We will focus on the discrete Fourier transform, which applies to discretely sampled signals (i.e., vectors). Linear algebra provides a simple way to think about the Fourier transform: it is simply a change of basis, specifically a mapping from the time domain to a representation in terms of a weighted combination of sinusoids of different frequencies. The discrete Fourier transform is therefore equiv- alent to multiplying by an orthogonal (or \unitary", which is the same concept when the entries are complex-valued) matrix1. For a vector of length N, the matrix that performs the DFT (i.e., that maps it to a basis of sinusoids) is an N × N matrix. The k'th row of this matrix is given by exp(−2πikt), for k 2 [0; :::; N − 1] (where we assume indexing starts at 0 instead of 1), and t is a row vector t=0:N-1;. Recall that exp(iθ) = cos(θ) + i sin(θ), so this gives us a compact way to represent the signal with a linear superposition of sines and cosines. The first row of the DFT matrix is all ones (since exp(0) = 1), and so the first element of the DFT corresponds to the sum of the elements of the signal. It is often known as the \DC component". The next row is a complex sinusoid that completes one cycle over the length of the signal, and each subsequent row has a frequency that is an integer multiple of this \fundamental" frequency. -

A Hilbert Space Theory of Generalized Graph Signal Processing
1 A Hilbert Space Theory of Generalized Graph Signal Processing Feng Ji and Wee Peng Tay, Senior Member, IEEE Abstract Graph signal processing (GSP) has become an important tool in many areas such as image pro- cessing, networking learning and analysis of social network data. In this paper, we propose a broader framework that not only encompasses traditional GSP as a special case, but also includes a hybrid framework of graph and classical signal processing over a continuous domain. Our framework relies extensively on concepts and tools from functional analysis to generalize traditional GSP to graph signals in a separable Hilbert space with infinite dimensions. We develop a concept analogous to Fourier transform for generalized GSP and the theory of filtering and sampling such signals. Index Terms Graph signal proceesing, Hilbert space, generalized graph signals, F-transform, filtering, sampling I. INTRODUCTION Since its emergence, the theory and applications of graph signal processing (GSP) have rapidly developed (see for example, [1]–[10]). Traditional GSP theory is essentially based on a change of orthonormal basis in a finite dimensional vector space. Suppose G = (V; E) is a weighted, arXiv:1904.11655v2 [eess.SP] 16 Sep 2019 undirected graph with V the vertex set of size n and E the set of edges. Recall that a graph signal f assigns a complex number to each vertex, and hence f can be regarded as an element of n C , where C is the set of complex numbers. The heart of the theory is a shift operator AG that is usually defined using a property of the graph. -
20. the Fourier Transform in Optics, II Parseval’S Theorem
20. The Fourier Transform in optics, II Parseval’s Theorem The Shift theorem Convolutions and the Convolution Theorem Autocorrelations and the Autocorrelation Theorem The Shah Function in optics The Fourier Transform of a train of pulses The spectrum of a light wave The spectrum of a light wave is defined as: 2 SFEt {()} where F{E(t)} denotes E(), the Fourier transform of E(t). The Fourier transform of E(t) contains the same information as the original function E(t). The Fourier transform is just a different way of representing a signal (in the frequency domain rather than in the time domain). But the spectrum contains less information, because we take the magnitude of E(), therefore losing the phase information. Parseval’s Theorem Parseval’s Theorem* says that the 221 energy in a function is the same, whether f ()tdt F ( ) d 2 you integrate over time or frequency: Proof: f ()tdt2 f ()t f *()tdt 11 F( exp(j td ) F *( exp(j td ) dt 22 11 FF() *(') exp([j '])tdtd ' d 22 11 FF( ) * ( ') [2 ')] dd ' 22 112 FF() *() d F () d * also known as 22Rayleigh’s Identity. The Fourier Transform of a sum of two f(t) F() functions t g(t) G() Faft() bgt () aF ft() bFgt () t The FT of a sum is the F() + sum of the FT’s. f(t)+g(t) G() Also, constants factor out. t This property reflects the fact that the Fourier transform is a linear operation. Shift Theorem The Fourier transform of a shifted function, f ():ta Ffta ( ) exp( jaF ) ( ) Proof : This theorem is F ft a ft( a )exp( jtdt ) important in optics, because we often encounter functions Change variables : uta that are shifting (continuously) along fu( )exp( j [ u a ]) du the time axis – they are called waves! exp(ja ) fu ( )exp( judu ) exp(jaF ) ( ) QED An example of the Shift Theorem in optics Suppose that we’re measuring the spectrum of a light wave, E(t), but a small fraction of the irradiance of this light, say , takes a different path that also leads to the spectrometer. -
The Fourier Transform
The Fourier Transform CS/CME/BIOPHYS/BMI 279 Fall 2015 Ron Dror The Fourier transform is a mathematical method that expresses a function as the sum of sinusoidal functions (sine waves). Fourier transforms are widely used in many fields of sciences and engineering, including image processing, quantum mechanics, crystallography, geoscience, etc. Here we will use, as examples, functions with finite, discrete domains (i.e., functions defined at a finite number of regularly spaced points), as typically encountered in computational problems. However the concept of Fourier transform can be readily applied to functions with infinite or continuous domains. (We won’t differentiate between “Fourier series” and “Fourier transform.”) A graphical example ! ! Suppose we have a function � � defined in the range − < � < on 2� + 1 discrete points such that ! ! ! � = �. By a Fourier transform we aim to express it as: ! !!!! � �! = �! + �! cos 2��!� + �! + �! cos 2��!� + �! + ⋯ (1) We first demonstrate graphically how a function may be described by its Fourier components. Fig. 1 shows a function defined on 101 discrete data points integer � = −50, −49, … , 49, 50. In fig. 2, the first Fig. 1. The function to be Fourier transformed few Fourier components are plotted separately (left) and added together (right) to form an approximation to the original function. Finally, fig. 3 demonstrates that by including the components up to � = 50, a faithful representation of the original function can be obtained. � ��, �� & �� Single components Summing over components up to m 0 �! = 0.6 �! = 0 �! = 0 1 �! = 1.9 �! = 0.01 �! = 2.2 2 �! = 0.27 �! = 0.02 �! = −1.3 3 �! = 0.39 �! = 0.03 �! = 0.4 Fig.2. -

Fourier Series, Haar Wavelets and Fast Fourier Transform
FOURIER SERIES, HAAR WAVELETS AND FAST FOURIER TRANSFORM VESA KAARNIOJA, JESSE RAILO AND SAMULI SILTANEN Abstract. This handout is for the course Applications of matrix computations at the University of Helsinki in Spring 2018. We recall basic algebra of complex numbers, define the Fourier series, the Haar wavelets and discrete Fourier transform, and describe the famous Fast Fourier Transform (FFT) algorithm. The discrete convolution is also considered. Contents 1. Revision on complex numbers 1 2. Fourier series 3 2.1. Fourier series: complex formulation 5 3. *Haar wavelets 5 3.1. *Theoretical approach as an orthonormal basis of L2([0, 1]) 6 4. Discrete Fourier transform 7 4.1. *Discrete convolutions 10 5. Fast Fourier transform (FFT) 10 1. Revision on complex numbers A complex number is a pair x + iy := (x, y) ∈ C of x, y ∈ R. Let z = x + iy, w = a + ib ∈ C be two complex numbers. We define the sum as z + w := (x + a) + i(y + b) • Version 1. Suggestions and corrections could be send to jesse.railo@helsinki.fi. • Things labaled with * symbol are supposed to be extra material and might be more advanced. • There are some exercises in the text that are supposed to be relatively easy, even trivial, and support understanding of the main concepts. These are not part of the official course work. 1 2 VESA KAARNIOJA, JESSE RAILO AND SAMULI SILTANEN and the product as zw := (xa − yb) + i(ya + xb). These satisfy all the same algebraic rules as the real numbers. Recall and verify that i2 = −1. However, C is not an ordered field, i.e. -

The Eigenvectors of the Discrete Fourier Transform: a Version of the Hermite Functions
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 88,355-363 (1982) The Eigenvectors of the Discrete Fourier Transform: A Version of the Hermite Functions F. ALBERTO GR~~NBAUM Mathematics Department, Unioersity of Calvomia, Berkeley, Calfornia 94720 Submitted by G.-C. Rota The matrix appearing in the discrete Fourier transform based on N points is given by Nm1/20(“m1)(tt--l) V-(W),., = 7 I < n, m < N, w = eiznjN. Its eigenvalues are + 1 and fi, a fact which has been rediscovered several times. The corresponding multiplicities have also been determined. In [2, 31 one finds these multiplicities and a complete set of eigenvectors. For a variety of proofs of these facts and more references, see [ 11. See also [4]. The purpose of this note is to exhibit, for each N, a tridiagonal matrix T(N) with (essentially) simple spectrum which commutes with F(N). Thus, the eigenvectors of T(N) give a “natural” basis of eigenvectors of F(N). We also treat the case of the centered discrete Fourier transform (see Section 2). In this latter case our tridiagonal matrix can be viewed as the discrete analogue of the Hermite operator showing up in Schroedinger’s equation for the harmonic oscillator. This analogy is spelled out later in the paper. In particular our tridiagonal matrix becomes, in the limit, the second- order Hermite differential operator. In general it is impossible to find a tridiagonal matrix with simple spectrum in the commutator of a given matrix. -

Fourier Analysis
Fourier Analysis Hilary Weller <[email protected]> 19th October 2015 This is brief introduction to Fourier analysis and how it is used in atmospheric and oceanic science, for: Analysing data (eg climate data) • Numerical methods • Numerical analysis of methods • 1 1 Fourier Series Any periodic, integrable function, f (x) (defined on [ π,π]), can be expressed as a Fourier − series; an infinite sum of sines and cosines: ∞ ∞ a0 f (x) = + ∑ ak coskx + ∑ bk sinkx (1) 2 k=1 k=1 The a and b are the Fourier coefficients. • k k The sines and cosines are the Fourier modes. • k is the wavenumber - number of complete waves that fit in the interval [ π,π] • − sinkx for different values of k 1.0 k =1 k =2 k =4 0.5 0.0 0.5 1.0 π π/2 0 π/2 π − − x The wavelength is λ = 2π/k • The more Fourier modes that are included, the closer their sum will get to the function. • 2 Sum of First 4 Fourier Modes of a Periodic Function 1.0 Fourier Modes Original function 4 Sum of first 4 Fourier modes 0.5 2 0.0 0 2 0.5 4 1.0 π π/2 0 π/2 π π π/2 0 π/2 π − − − − x x 3 The first four Fourier modes of a square wave. The additional oscillations are “spectral ringing” Each mode can be represented by motion around a circle. ↓ The motion around each circle has a speed and a radius. These represent the wavenumber and the Fourier coefficients. -
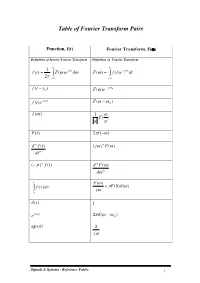
Table of Fourier Transform Pairs
Table of Fourier Transform Pairs Function, f(t) Fourier Transform, F() Definition of Inverse Fourier Transform Definition of Fourier Transform A A 1 f (t) * F()e j t d F() * f (t)e j t dt 2 A A jt f (t t0 ) F()e 0 j t f (t)e 0 F( 0 ) f (t) 1 F( ) F(t) 2 f () d n f (t) ( j) n F() dt n ( jt) n f (t) d n F() d n t F() F(0) () * f ( )d A j (t) 1 j t e 0 2 ( 0 ) sgn (t) 2 j Signals & Systems - Reference Tables 1 Fourier Transform Table UBC M267 Resources for 2005 F (t) F (ω) Notes (0) ∞ b iωt f(t) f(t)e− dt Definition. (1) Z−∞ 1 ∞ f(ω)eiωt dω f(ω) Inversion formula. (2) 2π Z−∞ b b f( t) 2πf(ω) Duality property. (3) − at 1 e−b u(t) a constant, e(a) > 0 (4) a + iω < a t 2a e− | | a constant, e(a) > 0 (5) a2 + ω2 < 1, if t < 1, sin(ω) β(t)= | | 2sinc(ω)=2 Boxcar in time. (6) 0, if t > 1 ω | | 1 sinc(t) β(ω) Boxcar in frequency. (7) π f 0(t) iωf(ω) Derivative in time. (8) 2 f 00(t) (iω)bf(ω) Higher derivatives similar. (9) d tf(t) i f(ω) Derivative in frequency. (10) dω b d2 t2f(t) i2 bf(ω) Higher derivatives similar. (11) dω2 iω0t e f(t) f(ω ω0) Modulation property.