Condensed Matter Physics 2016 Preliminary Planning 24/11 – 15/12
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![Arxiv:2005.03138V2 [Cond-Mat.Quant-Gas] 23 May 2020 Contents](https://docslib.b-cdn.net/cover/8131/arxiv-2005-03138v2-cond-mat-quant-gas-23-may-2020-contents-58131.webp)
Arxiv:2005.03138V2 [Cond-Mat.Quant-Gas] 23 May 2020 Contents
Condensed Matter Physics in Time Crystals Lingzhen Guo1 and Pengfei Liang2;3 1Max Planck Institute for the Science of Light (MPL), Staudtstrasse 2, 91058 Erlangen, Germany 2Beijing Computational Science Research Center, 100193 Beijing, China 3Abdus Salam ICTP, Strada Costiera 11, I-34151 Trieste, Italy E-mail: [email protected] Abstract. Time crystals are physical systems whose time translation symmetry is spontaneously broken. Although the spontaneous breaking of continuous time- translation symmetry in static systems is proved impossible for the equilibrium state, the discrete time-translation symmetry in periodically driven (Floquet) systems is allowed to be spontaneously broken, resulting in the so-called Floquet or discrete time crystals. While most works so far searching for time crystals focus on the symmetry breaking process and the possible stabilising mechanisms, the many-body physics from the interplay of symmetry-broken states, which we call the condensed matter physics in time crystals, is not fully explored yet. This review aims to summarise the very preliminary results in this new research field with an analogous structure of condensed matter theory in solids. The whole theory is built on a hidden symmetry in time crystals, i.e., the phase space lattice symmetry, which allows us to develop the band theory, topology and strongly correlated models in phase space lattice. In the end, we outline the possible topics and directions for the future research. arXiv:2005.03138v2 [cond-mat.quant-gas] 23 May 2020 Contents 1 Brief introduction to time crystals3 1.1 Wilczek's time crystal . .3 1.2 No-go theorem . .3 1.3 Discrete time-translation symmetry breaking . -

Solid State Physics II Level 4 Semester 1 Course Content
Solid State Physics II Level 4 Semester 1 Course Content L1. Introduction to solid state physics - The free electron theory : Free levels in one dimension. L2. Free electron gas in three dimensions. L3. Electrical conductivity – Motion in magnetic field- Wiedemann-Franz law. L4. Nearly free electron model - origin of the energy band. L5. Bloch functions - Kronig Penney model. L6. Dielectrics I : Polarization in dielectrics L7 .Dielectrics II: Types of polarization - dielectric constant L8. Assessment L9. Experimental determination of dielectric constant L10. Ferroelectrics (1) : Ferroelectric crystals L11. Ferroelectrics (2): Piezoelectricity L12. Piezoelectricity Applications L1 : Solid State Physics Solid state physics is the study of rigid matter, or solids, ,through methods such as quantum mechanics, crystallography, electromagnetism and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from their atomic- scale properties. Thus, solid-state physics forms the theoretical basis of materials science. It also has direct applications, for example in the technology of transistors and semiconductors. Crystalline solids & Amorphous solids Solid materials are formed from densely-packed atoms, which interact intensely. These interactions produce : the mechanical (e.g. hardness and elasticity), thermal, electrical, magnetic and optical properties of solids. Depending on the material involved and the conditions in which it was formed , the atoms may be arranged in a regular, geometric pattern (crystalline solids, which include metals and ordinary water ice) , or irregularly (an amorphous solid such as common window glass). Crystalline solids & Amorphous solids The bulk of solid-state physics theory and research is focused on crystals. -

Lecture 3: Fermi-Liquid Theory 1 General Considerations Concerning Condensed Matter
Phys 769 Selected Topics in Condensed Matter Physics Summer 2010 Lecture 3: Fermi-liquid theory Lecturer: Anthony J. Leggett TA: Bill Coish 1 General considerations concerning condensed matter (NB: Ultracold atomic gasses need separate discussion) Assume for simplicity a single atomic species. Then we have a collection of N (typically 1023) nuclei (denoted α,β,...) and (usually) ZN electrons (denoted i,j,...) interacting ∼ via a Hamiltonian Hˆ . To a first approximation, Hˆ is the nonrelativistic limit of the full Dirac Hamiltonian, namely1 ~2 ~2 1 e2 1 Hˆ = 2 2 + NR −2m ∇i − 2M ∇α 2 4πǫ r r α 0 i j Xi X Xij | − | 1 (Ze)2 1 1 Ze2 1 + . (1) 2 4πǫ0 Rα Rβ − 2 4πǫ0 ri Rα Xαβ | − | Xiα | − | For an isolated atom, the relevant energy scale is the Rydberg (R) – Z2R. In addition, there are some relativistic effects which may need to be considered. Most important is the spin-orbit interaction: µ Hˆ = B σ (v V (r )) (2) SO − c2 i · i × ∇ i Xi (µB is the Bohr magneton, vi is the velocity, and V (ri) is the electrostatic potential at 2 3 2 ri as obtained from HˆNR). In an isolated atom this term is o(α R) for H and o(Z α R) for a heavy atom (inner-shell electrons) (produces fine structure). The (electron-electron) magnetic dipole interaction is of the same order as HˆSO. The (electron-nucleus) hyperfine interaction is down relative to Hˆ by a factor µ /µ 10−3, and the nuclear dipole-dipole SO n B ∼ interaction by a factor (µ /µ )2 10−6. -

A Short Review of Phonon Physics Frijia Mortuza
International Journal of Scientific & Engineering Research Volume 11, Issue 10, October-2020 847 ISSN 2229-5518 A Short Review of Phonon Physics Frijia Mortuza Abstract— In this article the phonon physics has been summarized shortly based on different articles. As the field of phonon physics is already far ad- vanced so some salient features are shortly reviewed such as generation of phonon, uses and importance of phonon physics. Index Terms— Collective Excitation, Phonon Physics, Pseudopotential Theory, MD simulation, First principle method. —————————— —————————— 1. INTRODUCTION There is a collective excitation in periodic elastic arrangements of atoms or molecules. Melting transition crystal turns into liq- uid and it loses long range transitional order and liquid appears to be disordered from crystalline state. Collective dynamics dispersion in transition materials is mostly studied with a view to existing collective modes of motions, which include longitu- dinal and transverse modes of vibrational motions of the constituent atoms. The dispersion exhibits the existence of collective motions of atoms. This has led us to undertake the study of dynamics properties of different transitional metals. However, this collective excitation is known as phonon. In this article phonon physics is shortly reviewed. 2. GENERATION AND PROPERTIES OF PHONON Generally, over some mean positions the atoms in the crystal tries to vibrate. Even in a perfect crystal maximum amount of pho- nons are unstable. As they are unstable after some time of period they come to on the object surface and enters into a sensor. It can produce a signal and finally it leaves the target object. In other word, each atom is coupled with the neighboring atoms and makes vibration and as a result phonon can be found [1]. -

Introduction to Solid State Physics
Introduction to Solid State Physics Sonia Haddad Laboratoire de Physique de la Matière Condensée Faculté des Sciences de Tunis, Université Tunis El Manar S. Haddad, ASP2021-23-07-2021 1 Outline Lecture I: Introduction to Solid State Physics • Brief story… • Solid state physics in daily life • Basics of Solid State Physics Lecture II: Electronic band structure and electronic transport • Electronic band structure: Tight binding approach • Applications to graphene: Dirac electrons Lecture III: Introduction to Topological materials • Introduction to topology in Physics • Quantum Hall effect • Haldane model S. Haddad, ASP2021-23-07-2021 2 It’s an online lecture, but…stay focused… there will be Quizzes and Assignments! S. Haddad, ASP2021-23-07-2021 3 References Introduction to Solid State Physics, Charles Kittel Solid State Physics Neil Ashcroft and N. Mermin Band Theory and Electronic Properties of Solids, John Singleton S. Haddad, ASP2021-23-07-2021 4 Outline Lecture I: Introduction to Solid State Physics • A Brief story… • Solid state physics in daily life • Basics of Solid State Physics Lecture II: Electronic band structure and electronic transport • Tight binding approach • Applications to graphene: Dirac electrons Lecture III: Introduction to Topological materials • Introduction to topology in Physics • Quantum Hall effect • Haldane model S. Haddad, ASP2021-23-07-2021 5 Lecture I: Introduction to solid state Physics What is solid state Physics? Condensed Matter Physics (1960) solids Soft liquids Complex Matter systems Optical lattices, Non crystal Polymers, liquid crystal Biological systems (glasses, crystals, colloids s Economic amorphs) systems Neurosystems… S. Haddad, ASP2021-23-07-2021 6 Lecture I: Introduction to solid state Physics What is condensed Matter Physics? "More is different!" P.W. -
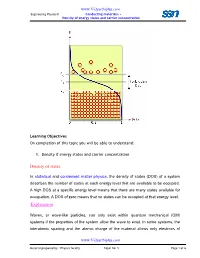
Density of States Explanation
www.Vidyarthiplus.com Engineering Physics-II Conducting materials- - Density of energy states and carrier concentration Learning Objectives On completion of this topic you will be able to understand: 1. Density if energy states and carrier concentration Density of states In statistical and condensed matter physics , the density of states (DOS) of a system describes the number of states at each energy level that are available to be occupied. A high DOS at a specific energy level means that there are many states available for occupation. A DOS of zero means that no states can be occupied at that energy level. Explanation Waves, or wave-like particles, can only exist within quantum mechanical (QM) systems if the properties of the system allow the wave to exist. In some systems, the interatomic spacing and the atomic charge of the material allows only electrons of www.Vidyarthiplus.com Material prepared by: Physics faculty Topic No: 5 Page 1 of 6 www.Vidyarthiplus.com Engineering Physics-II Conducting materials- - Density of energy states and carrier concentration certain wavelengths to exist. In other systems, the crystalline structure of the material allows waves to propagate in one direction, while suppressing wave propagation in another direction. Waves in a QM system have specific wavelengths and can propagate in specific directions, and each wave occupies a different mode, or state. Because many of these states have the same wavelength, and therefore share the same energy, there may be many states available at certain energy levels, while no states are available at other energy levels. For example, the density of states for electrons in a semiconductor is shown in red in Fig. -

Solid State Physics
1 Solid State Physics Semiclassical motion in a magnetic ¯eld 16 Lecture notes by Quantization of the cyclotron orbit: Landau levels 16 Michael Hilke Magneto-oscillations 17 McGill University (v. 10/25/2006) Phonons: lattice vibrations 17 Mono-atomic phonon dispersion in 1D 17 Optical branch 18 Experimental determination of the phonon Contents dispersion 18 Origin of the elastic constant 19 Introduction 2 Quantum case 19 The Theory of Everything 3 Transport (Boltzmann theory) 21 Relaxation time approximation 21 H2O - An example 3 Case 1: F~ = ¡eE~ 21 Di®usion model of transport (Drude) 22 Binding 3 Case 2: Thermal inequilibrium 22 Van der Waals attraction 3 Physical quantities 23 Derivation of Van der Waals 3 Repulsion 3 Semiconductors 24 Crystals 3 Band Structure 24 Ionic crystals 4 Electron and hole densities in intrinsic (undoped) Quantum mechanics as a bonder 4 semiconductors 25 Hydrogen-like bonding 4 Doped Semiconductors 26 Covalent bonding 5 Carrier Densities in Doped semiconductor 27 Metals 5 Metal-Insulator transition 27 Binding summary 5 In practice 28 p-n junction 28 Structure 6 Illustrations 6 One dimensional conductance 29 Summary 6 More than one channel, the quantum point Scattering 6 contact 29 Scattering theory of everything 7 1D scattering pattern 7 Quantum Hall e®ect 30 Point-like scatterers on a Bravais lattice in 3D 7 General case of a Bravais lattice with basis 8 superconductivity 30 Example: the structure factor of a BCC lattice 8 BCS theory 31 Bragg's law 9 Summary of scattering 9 Properties of Solids and liquids 10 single electron approximation 10 Properties of the free electron model 10 Periodic potentials 11 Kronig-Penney model 11 Tight binging approximation 12 Combining Bloch's theorem with the tight binding approximation 13 Weak potential approximation 14 Localization 14 Electronic properties due to periodic potential 15 Density of states 15 Average velocity 15 Response to an external ¯eld and existence of holes and electrons 15 Bloch oscillations 16 2 INTRODUCTION derived based on a periodic lattice. -

NMR for Condensed Matter Physics
Concise History of NMR 1926 ‐ Pauli’s prediction of nuclear spin Gorter 1932 ‐ Detection of nuclear magnetic moment by Stern using Stern molecular beam (1943 Nobel Prize) 1936 ‐ First theoretical prediction of NMR by Gorter; attempt to detect the first NMR failed (LiF & K[Al(SO4)2]12H2O) 20K. 1938 ‐ Prof. Rabi, First detection of nuclear spin (1944 Nobel) 2015 Maglab Summer School 1942 ‐ Prof. Gorter, first published use of “NMR” ( 1967, Fritz Rabi Bloch London Prize) Nuclear Magnetic Resonance 1945 ‐ First NMR, Bloch H2O , Purcell paraffin (shared 1952 Nobel Prize) in Condensed Matter 1949 ‐ W. Knight, discovery of Knight Shift 1950 ‐ Prof. Hahn, discovery of spin echo. Purcell 1961 ‐ First commercial NMR spectrometer Varian A‐60 Arneil P. Reyes Ernst 1964 ‐ FT NMR by Ernst and Anderson (1992 Nobel Prize) NHMFL 1972 ‐ Lauterbur MRI Experiment (2003 Nobel Prize) 1980 ‐ Wuthrich 3D structure of proteins (2002 Nobel Prize) 1995 ‐ NMR at 25T (NHMFL) Lauterbur 2000 ‐ NMR at NHMFL 45T Hybrid (2 GHz NMR) Wuthrichd 2005 ‐ Pulsed field NMR >60T Concise History of NMR ‐ Old vs. New Modern Developments of NMR Magnets Technical improvements parallel developments in electronics cryogenics, superconducting magnets, digital computers. Advances in NMR Magnets 70 100T Superconducting 60 Resistive Hybrid 50 Pulse 40 Nb3Sn 30 NbTi 20 MgB2, HighTc nanotubes 10 0 1950 1960 1970 1980 1990 2000 2010 2020 2030 NMR in medical and industrial applications ¬ MRI, functional MRI ¬ non‐destructive testing ¬ dynamic information ‐ motion of molecules ¬ petroleum ‐ earth's field NMR , pore size distribution in rocks Condensed Matter ChemBio ¬ liquid chromatography, flow probes ¬ process control – petrochemical, mining, polymer production. -

Condensed Matter Option MAGNETISM Handout 1
Condensed Matter Option MAGNETISM Handout 1 Hilary 2014 Radu Coldea http://www2.physics.ox.ac.uk/students/course-materials/c3-condensed-matter-major-option Syllabus The lecture course on Magnetism in Condensed Matter Physics will be given in 7 lectures broken up into three parts as follows: 1. Isolated Ions Magnetic properties become particularly simple if we are able to ignore the interactions between ions. In this case we are able to treat the ions as effectively \isolated" and can discuss diamagnetism and paramagnetism. For the latter phenomenon we revise the derivation of the Brillouin function outlined in the third-year course. Ions in a solid interact with the crystal field and this strongly affects their properties, which can be probed experimentally using magnetic resonance (in particular ESR and NMR). 2. Interactions Now we turn on the interactions! I will discuss what sort of magnetic interactions there might be, including dipolar interactions and the different types of exchange interaction. The interactions lead to various types of ordered magnetic structures which can be measured using neutron diffraction. I will then discuss the mean-field Weiss model of ferromagnetism, antiferromagnetism and ferrimagnetism and also consider the magnetism of metals. 3. Symmetry breaking The concept of broken symmetry is at the heart of condensed matter physics. These lectures aim to explain how the existence of the crystalline order in solids, ferromagnetism and ferroelectricity, are all the result of symmetry breaking. The consequences of breaking symmetry are that systems show some kind of rigidity (in the case of ferromagnetism this is permanent magnetism), low temperature elementary excitations (in the case of ferromagnetism these are spin waves, also known as magnons), and defects (in the case of ferromagnetism these are domain walls). -

Problems for Condensed Matter Physics (3Rd Year Course B.VI) A
1 Problems for Condensed Matter Physics (3rd year course B.VI) A. Ardavan and T. Hesjedal These problems are based substantially on those prepared anddistributedbyProfS.H.Simonin Hilary Term 2015. Suggested schedule: Problem Set 1: Michaelmas Term Week 3 • Problem Set 2: Michaelmas Term Week 5 • Problem Set 3: Michaelmas Term Week 7 • Problem Set 4: Michaelmas Term Week 8 • Problem Set 5: Christmas Vacation • Denotes crucial problems that you need to be able to do in your sleep. *Denotesproblemsthatareslightlyharder.‡ 2 Problem Set 1 Einstein, Debye, Drude, and Free Electron Models 1.1. Einstein Solid (a) Classical Einstein Solid (or “Boltzmann” Solid) Consider a single harmonic oscillator in three dimensions with Hamiltonian p2 k H = + x2 2m 2 ◃ Calculate the classical partition function dp Z = dx e−βH(p,x) (2π!)3 ! ! Note: in this problem p and x are three dimensional vectors (they should appear bold to indicate this unless your printer is defective). ◃ Using the partition function, calculate the heat capacity 3kB. ◃ Conclude that if you can consider a solid to consist of N atoms all in harmonic wells, then the heat capacity should be 3NkB =3R,inagreementwiththelawofDulongandPetit. (b) Quantum Einstein Solid Now consider the same Hamiltonian quantum mechanically. ◃ Calculate the quantum partition function Z = e−βEj j " where the sum over j is a sum over all Eigenstates. ◃ Explain the relationship with Bose statistics. ◃ Find an expression for the heat capacity. ◃ Show that the high temperature limit agrees with the law of Dulong of Petit. ◃ Sketch the heat capacity as a function of temperature. 1.2. Debye Theory (a) State the assumptions of the Debye model of heat capacity of a solid. -

“Crystallography and Photonics” Russian Academy of Science
Federal Scientific Research Center “Crystallography and Photonics” Russian Academy of Science (FSRC «Crystallography and Photonics» RAS) Olga Alekseeva, Director Moscow, Russia FSRC “Crystallography and Photonics” RAS Established in 2016 on the basis of Shubnikov Institute of Crystallography on the initiative of Prof. M.Kovalchuk and Academiсian V.Panchenko, now the scientific leaders of the Center Subdivisions Branches Laboratory on Space Shubnikov Institute of 75 years Crystallography in 2018 Materials Science of IC RAS (IC RAS, Moscow ) (LCM IC RAS, Kaluga ) Image processing systems Institute of Photon Institute ( IPSI RAS, Samara ) Technologies (IPT RAS, Moscow ) Institute on Laser and Photochemistry Centre Information Technologies (PC RAS, Moscow ) (ILIT RAS, Shatura ) Crystallography: stages of development Starting as the mineralogical science, crystallography became an interdisciplinary science, where the achievements of chemistry, biology, physics, and geology are mixed and complementary. Physics Biology Mineralogy Crystallography: stages of development Shubnikov Institute of Crystallography – research ideology that is based on the “growth– structure–properties” triad with a deep relationship between these concepts. During 75 years our institute went the same way as the science of crystallography and now our research fields are including mineralogy, chemistry, chemical analysis, crystal growth, X- ray diffraction analysis, physical materials science and also biology and protein crystallography. Physics Biology Structure Growth -

Statistical and Dynamical Aspects of Mesoscopic Systems
Lecture Notes in Physics 547 Statistical and Dynamical Aspects of Mesoscopic Systems Proceedings of the XVI Sitges Conference on Statistical Mechanics Held at Sitges, Barcelona, Spain, 7–11 June 1999 Bearbeitet von D Reguera, G Platero, L.L Bonilla, J.M Rubi 1. Auflage 2000. Buch. xii, 360 S. Hardcover ISBN 978 3 540 67478 8 Format (B x L): 15,5 x 23,5 cm Gewicht: 725 g Weitere Fachgebiete > Physik, Astronomie > Angewandte Physik Zu Inhaltsverzeichnis schnell und portofrei erhältlich bei Die Online-Fachbuchhandlung beck-shop.de ist spezialisiert auf Fachbücher, insbesondere Recht, Steuern und Wirtschaft. Im Sortiment finden Sie alle Medien (Bücher, Zeitschriften, CDs, eBooks, etc.) aller Verlage. Ergänzt wird das Programm durch Services wie Neuerscheinungsdienst oder Zusammenstellungen von Büchern zu Sonderpreisen. Der Shop führt mehr als 8 Millionen Produkte. Preface One of the most significant developments in physics in recent years con- cerns mesoscopic systems, a subfield of condensed matter physics which has achieved proper identity. The main objective of mesoscopic physics is to un- derstand the physical properties of systems that are not as small as single atoms, but small enough that properties can differ significantly from those of a large piece of material. This field is not only of fundamental interest in its own right, but it also offers the possibility of implementing new generations of high-performance nano-scale electronic and mechanical devices. In fact, interest in this field has been initiated at the request of modern electronics which demands the development of more and more reduced structures. Un- derstanding the unusual properties these structures possess requires collabo- ration between disparate disciplines.