A General Check Digit System Based on Finite Groups
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Country Code Country Name National Client Identifier Format
Country Country National client Format of the identifier Potential source of the information code name identifier AT Austria CONCAT Belgian National Number 11 numerical digits where the first 6 are the date of birth (YYMMDD), the next 3 are an BE Belgium (Numéro de registre National ID ordering number (uneven for men, even for women) and the last 2 a check digit. national - Rijksregisternummer) CONCAT It consists of 10 digits. The first 6 are the date of birth (YYMMDD). The next 3 digits Bulgarian Personal have information about the area in Bulgaria and the order of birth, and the ninth digit is BG Bulgaria Passport, National ID, Driving Licence Number even for a boy and odd for a girl. Seventh and eighth are randomly generated according to the city. The tenth digit is a check digit. CONCAT The number for passports issued before 13/12/2010 consists of the character 'E' The passport is issued by the Civil National Passport CY Cyprus followed by 6 digits i.e E123456. Biometric passports issued after 13/12/2010 have a Registry Department of the Ministry Number number that starts with the character 'K', followed by 8 digits. i.e K12345678 of Interior. CONCAT It is a nine or ten-digit number in the format of YYXXDD/SSSC, where XX=MM (month of birth) for male, i.e. numbers 01-12, and XX=MM+50 (or exceptionally XX=MM+70) for female, i.e. numbers 51-62 (or 71-82). For example, a number 785723 representing the It is assigned to a person shortly after first six digits is assigned to a woman born on 23rd of July 1978. -

EGON for Anacredit EGON for Anacredit
EGON for AnaCredit EGON for AnaCredit The AnaCredit project involves creating a new database for the regulation of bank loans at European level. AnaCredit The European Central Bank thus requires individual Banks, through their National Central Banks, to collect a very detailed and granular set of data, including master data and addresses. This request is currently limited to legal entities, but it will also be extended to private individuals. EGON offers specific tools to support banks in transmitting this information to the ECB in a unique, codified manner in accordance with established European standards. In particular, EGON for AnaCredit is able to manage and standardize the following information: Address with NUTS encoding attribution National Identifier (e.g. tax codes, tax IDs, or other national identifiers) Legal Forms (Legal Forms of Each EU Country) LEI (Legal entities identifier) Classification of economic activities (transcoded in NACE coding) Managed information Address National Identifier The address must be provided according to the structure The National Identifier is a national identification code that below, with the attribution of the NUTS3 encoding, allowing uniquely identifies a physical or legal entity. The composition of EGON to manage at EU level: National Identifiers is different for each country. EGON allows • street validating all National Identifiers by applying specific logic and • city/town/village algorithms for each country. • county/admin. division standard NUTS 3 • postal code • country Legal Form LEI Classification of economic activities The classification of legal forms takes on a The LEI code is a unique and global 20-byte The transmission of information on the unified European coding according to the alphanumeric identifier assigned to classification of economic activities in the standard defined by the ECB. -

By GS1 Member Organisation Overview of How GS1 Prefixes for 'National' Solutions Are Used by Each GS1 Member Organisation
Summary of GS1 Prefixes 20 - 29 by GS1 Member Organisation overview of how GS1 Prefixes for 'national' solutions are used by each GS1 Member Organisation Release 5.1.2, Draft, Apr 2021 Summary of GS1 Prefixes 20 - 29 by GS1 Member Organisation Document Summary Document Item Current Value Document Name Summary of GS1 Prefixes 20 - 29 by GS1 Member Organisation Document Date Apr 2021 Document Version 5.1 Document Issue 2 Document Status Draft Document Description overview of how GS1 Prefixes for 'national' solutions are used by each GS1 Member Organisation Contributors GS1 Global Offices expresses its thanks to all those individuals, who are too numerous to list here, who have provided input to this publication. Log of Changes Release Date of Change Changed By Summary of Change 1. October 2006 D. Buckley New – application of GS1 format to previous version. 2 June 2007 D. Buckley Multiple updates and refresh 3.0 October 2011 D.Buckley Multiple updates and GS1 branding 4.0 May 2012 D.Buckley Major refresh, update on Produce and Coupon information and reconfirmation of data: Argentina: new coupon Albania: new Belgium: updated Brazil: updated Columbia: confirmed China: updated Denmark: confirmed Iceland: update Iran: new Italy: confirmed Jordan: confirmed/updated Kenya: new Nederland: confirmed/updated Nigeria: new Russia: confirmed/updated Slovenia: confirmed Tanzania: new Tunisia: new 4.1 1 June 2012 D.Buckley Australia: update Release 5.1.2, Draft, Apr 2021 © 2021 GS1 AISBL Page 2 of 94 Summary of GS1 Prefixes 20 - 29 by GS1 Member Organisation -
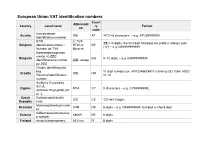
European Union VAT Identification Numbers Count Abbreviati Country Local Name Ry Format on Code Umsatzsteuer- Austria UID at 'ATU'+8 Characters, – E.G
European Union VAT identification numbers Count Abbreviati Country Local name ry Format on code Umsatzsteuer- Austria UID AT 'ATU'+8 characters, – e.g. ATU99999999 Identifikationsnummer BTW n° TVA 'BE'+10 digits, the first digit following the prefix is always zero Belgium identificatienummer / BTW-nr BE ("0") – e.g. BE0999999999 Numéro de TVA Mwst-nr Идентификационен номер по ДДС Bulgaria BG 9–10 digits – e.g. BG999999999 Identifikacionen nomer ДДС номер po DDS Osobni identifikacijski broj 11 digit number (ex. HR12345678901) utilising ISO 7064, MOD Croatia OIB HR Personal identification 11-10 number Αριθμός Εγγραφής Φ.Π.Α. Cyprus ΦΠΑ CY 9 characters – e.g. CY99999999L Arithmós Engraphḗs phi. pi. a. Czech Daňové identifikační DIČ CZ 'CZ'+8-10 digits Republic číslo Momsregistreringsnumm Denmark CVR DK 8 digits – e.g. DK99999999, last digit is check digit er Käibemaksukohustuslas Estonia KMKR EE 9 digits e number Finland Arvonlisäveronumero ALV nro FI 8 digits 'FR'+ 2 digits (as validation key ) + 9 digits (as SIREN), the first and/or the second value can also be a character – e.g. Numéro d'identification à FRXX999999999 la taxe sur la valeur The French key is calculated as follow : Key = [ 12 + 3 * ( France ajoutée / Numéro de n° TVA FR SIREN modulo 97 ) ] modulo 97, for example : Key = [ 12 + 3 * ( TVA 404,833,048 modulo 97 ) ] modulo 97 = [12 + 3*56] modulo 97 = intracommunautaire 180 modulo 97 = 83 so the tax number for 404,833,048 is FR 83,404,833,048 source from : www.insee.fr Umsatzsteuer- Germany USt-IdNr. DE 9 digits Identifikationsnummer Αριθμός Φορολογικού Μητρώου Greece ΑΦΜ EL 9 digits, last one is a check digit Arithmós Phorologikoú Mētrṓou Hungary Közösségi adószám ANUM HU 8 digits – e.g. -

Towards Safer Medicines Supply
Towards safer medicines supply A vision for the coding and identification of pharmaceutical products in Europe Business Case Version 4.0 January 2008 Abstract The pharmaceutical supply chain in Europe has become increasingly complex, with billions of medicine packs moving around the EU each year. Its fragmentation as well as the overwhelming growth of wholesaler intermediaries and traders involved in the European flow of medicines have resulted in a decreased transparency of the supply chain, and an increase in the difficulties to track and trace medicines. In addition, recent cases relating to counterfeit medicines have shown that integrity of the supply chain in Europe is at risk. Against this background, national requirements governing the identification and traceability of pharmaceuticals have become a growing trend in Europe. However, there currently exists no industry recognised standard for the identification and coding of pharmaceutical products. Instead, there are an increasing number of different local coding systems being implemented or proposed across Europe, which only contributes to the increased fragmentation of the supply chain. It has therefore become clear that an integrated approach to tackling the supply chain problems has become essential. This has led the research-based pharmaceutical industry, through EFPIA, to recommend the implementation of a standardized and unique coding solution for medicines at European level. The key to delivering a successful product security solution will be to work together with all parties holding stakes in the identification of medicines (i.e. pharmacists, wholesalers, manufacturers, governments, EU Authorities, etc) to deliver an adequate legal, political and operational framework to support the integration of a technology system at the European level, which has the support of the national and EU authorities. -

A Concise Guide to Book Industry Product Identifiers
AA CCoonncciissee GGuuiiddee ttoo BBooookk IInndduussttrryy PPrroodduucctt IIddeennttiiffiieerrss Drafted by the ISBN-13 Task Force of the Book Industry Study Group, Inc. ISBN-10 International Standard Book Number (in its ten-digit form) • Used worldwide for over thirty years • Hyphenation & spacing: May be presented with or without hyphens or spaces between its elements. When the intention is to present the ISBN in a “human- readable” form (e.g., above the bar code, on the copyright page, in a printed catalog, etc.) hyphens or spaces are required and the number must be preceded by the abbreviation “ISBN”. • Should only be used on books published before 2007 • Bar coding: Must be converted to a Bookland EAN/UCC-13 to be bar coded • Not a part of the GTIN family of numbers ISBN-13 International Standard Book Number (in its thirteen-digit form) • The exclusive form of the ISBN for all books published after 2006 • Hyphenation & spacing: May be presented with or without hyphens or spaces between its elements. When the intention is to present the ISBN in a “human- readable” form (e.g., above the bar code, on the copyright page, in a printed catalog, etc.) hyphens or spaces are required and the number must be preceded by the abbreviation “ISBN”. • Should be used (in conjunction with the ISBN-10) on books published before 2007 whenever such a practice is feasible • Should only be used on books and book-related products as defined in the ISBN Standard (ISO 2108) and the contract between ISBN International and GS1 • Equivalent (in its non-hyphenated form) to the Bookland EAN/UCC-13 • Bar coding: Uses a standard EAN/UCC-13 bar code (with or without five-digit price add-on) • May be easily converted to a GTIN-14 Page 1 of 5 Last Revised 08/12/2005 © 2005, The Book Industry Study Group, Inc. -

Tax ID Table
Country Flag Country Name Tax Identification Number (TIN) type TIN structure Where to find your TIN For individuals, the TIN consists of the letter "E" or "F" followed by 6 numbers and 1 control letter. TINs for Número d’Identificació residents start with the letter "F." TINs for non-residents AD Andorra Administrativa (NIA) start with the letter "E". AI Anguilla N/A All individuals and businesses receive a TIN (a 6-digit number) when they register with the Inland Revenue Department. See http://forms.gov. AG Antigua & Barbuda TIN A 6-digit number. ag/ird/pit/F50_Monthly_Guide_Individuals2006.pdf CUIT. Issued by the AFIP to any individual that initiates any economic AR Argentina activity. The CUIT consists of 11 digits. The TIN is generated by an automated system after registering relevant AW Aruba TIN An 8-digit number. data pertaining to a tax payer. Individuals generally use a TFN to interact with the Australian Tax Office for various purposes and, therefore, most individuals have a TFN. This includes submitting income tax returns, reporting information to the ATO, obtaining The Tax File Number (TFN) is an eight- or nine-digit government benefits and obtaining an Australian Business Number (ABN) AU Australia Tax File Number (TFN) number compiled using a check digit algorithm. in order to maintain a business. TINs are only issued to individuals who are liable for tax. They are issued by the Local Tax Office. When a person changes their residence area, the TIN AT Austria TIN Consists of 9 digits changes as well. TINs are only issued to people who engage in entrepreneurial activities and AZ Azerbaijan TIN TIN is a ten-digit code. -

IBAN Formats by Country
IBAN Formats By Country The kk after the two-character ISO country code represents the check digits calculated from the rest of the IBAN characters. If it is a constant for the country concerned, this will be stated in the Comments column. This happens where the BBAN has its own check digits that use the same algorithm as the IBAN check digits. The BBAN format column shows the format of the BBAN part of an IBAN in terms of upper case alpha characters (A–Z) denoted by "a", numeric characters (0–9) denoted by "n" and mixed case alphanumeric characters (a–z, A–Z, 0–9) denoted by "c". For example, the Bulgarian BBAN (4a,6n,8c) consists of 4 alpha characters, followed by 6 numeric characters, then by 8 mixed-case alpha-numeric characters. Descriptions in the Comments field have been standardised with country specific names in brackets. The format of the various fields can be deduced from the BBAN field. Countries that are planning to introduce the IBAN are shown in italics with the planned date of introduction in bold. BBAN Country Chars IBAN Fields Comment Format b = National bank code s = Branch code Albania 28 8n, 16c ALkk bbbs sssx cccc cccc cccc cccc x = National check digit c = Account number b = National bank code Andorra 24 8n,12c ADkk bbbb ssss cccc cccc cccc s = Branch code c = Account number b = National bank code Austria 20 16n ATkk bbbb bccc cccc cccc c = Account number b = National bank code Azerbaijan 28 4c,20n AZkk bbbb cccc cccc cccc cccc cccc c = Account number b = National bank code Bahrain 22 4a,14c BHkk bbbb cccc cccc cccc -

Common Reporting Standard
COMMON REPORTING STANDARD TAX IDENTIFICATION NUMBERS LEAFLET Version updated as of October 31th, 2019 Disclaimer: The present informative document, subject to modification, is communicated for information purposes only and has no contractual value. This document is defined based on the information provided by the OECD portal. It contains information that it is the sole responsibility of each country and is (i) of a general nature only and not intended to address the specific circumstances of any particular individual or entity, (ii) not necessarily comprehensive, complete, accurate or up to date,(iii) sometimes linked to external sites over which SG Group has no control and for which SG Group assumes no responsibility and (iv) not professional or legal advice. If you need specific advice, you should always consult a professional tax advisor. TAX IDENTIFICATION NUMBERS This document provides an overview of domestic rules in the countries listed below governing the issuance, structure, use and validity of Tax Identification Numbers (“TIN”) or their functional equivalents. It is split into two sections: Countries that have already published the information on the OECD portal and can 1 be accessed by clicking on the name of the country below Cook Andorra Hungary Malaysia Saudi Arabia Islands Argentina Costa Rica Iceland Malta Seychelles Marshall Aruba Croatia India Islands Singapore Australia Curacao Indonesia Mauritius Slovak Republic Ireland Austria Mexico Cyprus Slovenia Isle of Man Azerbaijan Czech Montserrat Republic South Africa Bahrain -

Integrating Unique Identification Numbers in Civil Registration
Integrating Unique Identification Numbers In Civil Registration © 2018 International Bank for Reconstitution and Development/The World Bank 1818 H Street, NW, Washington, D.C., 20433 Telephone: 202-473-1000; Internet: www.worldbank.org Some Rights Reserved This work is a product of the staff of The World Bank with external contributions. The findings, interpretations, and conclusions expressed in this work do not necessarily reflect the views of The World Bank, its Board of Executive Directors, or the governments they represent. The World Bank does not guarantee the accuracy of the data included in this work. The boundaries, colors, denominations, and other information shown on any map in this work do not imply any judgment on the part of The World Bank concerning the legal status of any territory or the endorsement or acceptance of such boundaries. Nothing herein shall constitute or be considered to be a limitation upon or waiver of the privileges and immunities of The World Bank, or of any participating organization to which such privileges and immunities may apply, all of which are specifically reserved. Rights and Permission This work is available under the Creative Commons Attribution 3.0 IGO license (CC BY 3.0 IGO) http://creativecommons. org/licenses/by/3.0/igo. Under the Creative Commons Attribution license, you are free to copy, distribute, transmit, and adapt this work, including for commercial purposes, under the following conditions: Attribution—Please cite the work as follows: World Bank. 2016. Integrating Unique Identification Numbers in Civil Registration, Washington, DC: World Bank License: Creative Commons Attribution 3.0 IGO (CC BY 3.0 IGO) Translations—If you create a translation of this work, please add the following disclaimer along with the attribution: This translation was not created by The World Bank and should not be considered an official World Bank translation. -

Geographical Classification Is Provided for the Guidance of Reporting Institutions in Preparing Reports on the Treasury International Capital (TIC) Forms
DEPARTMENT OF THE TREASURY JANUARY 2001 Revised August 2002 Revised January 2006 Revised April 2006 APPENDIX G E O G R A P H I C A L C L A S S I F I C A T I O N TO BE USED FOR PURPOSES OF REPORTING ON TREASURY INTERNATIONAL CAPITAL FORMS , THIS APPENDIX APPLIES ONLY TO REPORTS WITH AS-OF DATES ON OR AFTER JUNE 30, 2006 EXPLANATORY NOTE This geographical classification is provided for the guidance of reporting institutions in preparing reports on the Treasury International Capital (TIC) Forms. The coding system has been developed for use by the Federal Reserve Banks and the Treasury in processing the TIC Forms. Reporting institutions filing their reports on magnetic tape or other media that can be processed by data processing equipment are required to use these codes. In addition to the codes shown for countries and areas listed separately on the reporting forms themselves, codes have also been assigned to certain named places that are components of those countries and geographical categories. The latter codes, which are followed by an asterisk (*), are provided for the convenience of respondents, who may wish to adopt them for internal use. The first four digits of the country code represent the actual code. The fifth number is a check digit calculated by the “Modulus 11 Method.” Short descriptions of the revisions are on the last page. 1 Country, Area and Organizational Codes EUROPE ALBANIA 15105 ANDORRA 10103 ARMENIA 16519 AUSTRIA 10189 AZERBAIJAN 16527 BANK FOR INTERNATIONAL SETTLEMENTS 13307 BELARUS 16209 BELGIUM 10251 BOSNIA AND HERZEGOVINA 14109 BULGARIA 15202 CROATIA 14214 CYPRUS 10405 CZECH REPUBLIC 15288 DENMARK Excluding Faroe Islands and Greenland 10502 ESTONIA 15407 EUROPEAN CENTRAL BANK 13501 FAROE ISLANDS 10618 FINLAND: Including Ahvenanamaa (Aland Islands) 10707 FRANCE Excluding Andorra, French Guiana, Guadeloupe, Martinique, 10804 Mayotte, Monaco, Reunion, and St. -

(EU) 2015/ 2366 Of
11.11.2017 ANNEX I Format of the relevant unique identification number in each Member State Legal person Natural person Member State ID number type ID number format ID number type ID number format EN If registered: If not registered: Firmenbuchnummer (https://www.justiz.gv. Maximum: six digits plus one Austria — at/web2013/html/default/ check letter Umsatzsteuer-Identifikations-Nummer (UID-Nummer) (https://www.bmf.gv. 8ab4a8a422985de30122a90fc2ca620b.de. at/steuern/selbststaendige-unternehmer/umsatzsteuer/UID-und-ZM.html) html) KBO/BCE number (KBO = KruispuntBank van Ondernemingen; BCE = Banque-Carrefour des KBO/BCE number (KBO, KruispuntBank van Ondernemingen; BCE, Official 0 + VAT number 10 digits (0 + 9 digit- Belgium Entreprises) Banque-Carrefour des Entreprises) (0XXX.XXX.XXX) VAT number) http://economie.fgov. http://economie.fgov.be/nl/ondernemingen/KBO/#.VlbmZpYcTcu be/nl/ondernemingen/KBO/#.VlbmZpYcTcu Jour nal Unified Identification Code' as regulated by of Unified Identification Code' as regulated by Art. 23, para. 1 of the Bulgarian Bulgaria Art. 23, para. 1 of the Bulgarian Commercial 9 digits 9 digits the Commercial Register Act. Register Act. European OIB 11 digits 11 digits OIB Croatia (fiscal number; Osobni identifikacijski broj — (10 random digits + 1 check (10 random di Union (fiscal number; Osobni identifikacijski broj — Personal Identification Number) Personal Identification Number) digit) gits + 1 check digit) Tax Identification Number (TIN) 8 digits and 1 letter Tax Identification Code (TIC) 8 digits and 1 letter (the Cyprus https://ec.europa.eu/taxation_ (e.g: 99999999L) https://ec.europa.eu/taxation_customs/tin/tinByCountry.html first digit is always zero) customs/tin/tinByCountry.html Personal identification number (Identifikační Czech Republic 8 digits (e.g.:12345678) Personal identification number (Identifikační číslo osoby (IČO)) 8 digits (e.g.