Dynamical Simulation of Effective Stem Cell Transplantation for Modulation of Microglia Responses in Stroke Treatment
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Act of Controlling Adult Stem Cell Dynamics: Insights from Animal Models
biomolecules Review The Act of Controlling Adult Stem Cell Dynamics: Insights from Animal Models Meera Krishnan 1, Sahil Kumar 1, Luis Johnson Kangale 2,3 , Eric Ghigo 3,4 and Prasad Abnave 1,* 1 Regional Centre for Biotechnology, NCR Biotech Science Cluster, 3rd Milestone, Gurgaon-Faridabad Ex-pressway, Faridabad 121001, India; [email protected] (M.K.); [email protected] (S.K.) 2 IRD, AP-HM, SSA, VITROME, Aix-Marseille University, 13385 Marseille, France; [email protected] 3 Institut Hospitalo Universitaire Méditerranée Infection, 13385 Marseille, France; [email protected] 4 TechnoJouvence, 13385 Marseille, France * Correspondence: [email protected] Abstract: Adult stem cells (ASCs) are the undifferentiated cells that possess self-renewal and differ- entiation abilities. They are present in all major organ systems of the body and are uniquely reserved there during development for tissue maintenance during homeostasis, injury, and infection. They do so by promptly modulating the dynamics of proliferation, differentiation, survival, and migration. Any imbalance in these processes may result in regeneration failure or developing cancer. Hence, the dynamics of these various behaviors of ASCs need to always be precisely controlled. Several genetic and epigenetic factors have been demonstrated to be involved in tightly regulating the proliferation, differentiation, and self-renewal of ASCs. Understanding these mechanisms is of great importance, given the role of stem cells in regenerative medicine. Investigations on various animal models have played a significant part in enriching our knowledge and giving In Vivo in-sight into such ASCs regulatory mechanisms. In this review, we have discussed the recent In Vivo studies demonstrating the role of various genetic factors in regulating dynamics of different ASCs viz. -

Regulation of Adult Neurogenesis in Mammalian Brain
International Journal of Molecular Sciences Review Regulation of Adult Neurogenesis in Mammalian Brain 1,2, 3, 3,4 Maria Victoria Niklison-Chirou y, Massimiliano Agostini y, Ivano Amelio and Gerry Melino 3,* 1 Centre for Therapeutic Innovation (CTI-Bath), Department of Pharmacy & Pharmacology, University of Bath, Bath BA2 7AY, UK; [email protected] 2 Blizard Institute of Cell and Molecular Science, Barts and the London School of Medicine and Dentistry, Queen Mary University of London, London E1 2AT, UK 3 Department of Experimental Medicine, TOR, University of Rome “Tor Vergata”, 00133 Rome, Italy; [email protected] (M.A.); [email protected] (I.A.) 4 School of Life Sciences, University of Nottingham, Nottingham NG7 2HU, UK * Correspondence: [email protected] These authors contributed equally to this work. y Received: 18 May 2020; Accepted: 7 July 2020; Published: 9 July 2020 Abstract: Adult neurogenesis is a multistage process by which neurons are generated and integrated into existing neuronal circuits. In the adult brain, neurogenesis is mainly localized in two specialized niches, the subgranular zone (SGZ) of the dentate gyrus and the subventricular zone (SVZ) adjacent to the lateral ventricles. Neurogenesis plays a fundamental role in postnatal brain, where it is required for neuronal plasticity. Moreover, perturbation of adult neurogenesis contributes to several human diseases, including cognitive impairment and neurodegenerative diseases. The interplay between extrinsic and intrinsic factors is fundamental in regulating neurogenesis. Over the past decades, several studies on intrinsic pathways, including transcription factors, have highlighted their fundamental role in regulating every stage of neurogenesis. However, it is likely that transcriptional regulation is part of a more sophisticated regulatory network, which includes epigenetic modifications, non-coding RNAs and metabolic pathways. -

Rapid and Efficient Generation of Oligodendrocytes from Human
Rapid and efficient generation of oligodendrocytes PNAS PLUS from human induced pluripotent stem cells using transcription factors Marc Ehrlicha,b, Sabah Mozafaric,d,e,f, Michael Glatzab, Laura Starosta,b, Sergiy Velychkob, Anna-Lena Hallmanna,b, Qiao-Ling Cuig, Axel Schambachh, Kee-Pyo Kimb, Corinne Bachelinc,d,e,f, Antoine Marteync,d,e,f, Gunnar Hargusa,b, Radia Marie Johnsoni, Jack Antelg, Jared Sterneckertj, Holm Zaehresb,k, Hans R. Schölerb,l, Anne Baron-Van Evercoorenc,d,e,f, and Tanja Kuhlmanna,1 aInstitute of Neuropathology, University Hospital Münster, 48149 Muenster, Germany; bDepartment of Cell and Developmental Biology, Max Planck Institute for Molecular Biomedicine, 48149 Muenster, Germany; cINSERM, U1127, F-75013 Paris, France; dCNRS, UMR 7225, F-75013 Paris, France; eSorbonne Universités, Université Pierre et Marie Curie Paris 06, UM-75, F-75005 Paris, France; fInstitut du Cerveau et de la Moelle epinière-Groupe Hospitalier Pitié-Salpêtrière, F-75013 Paris, France; gMontreal Neurological Institute, McGill University, Montreal, QC, Canada H3A 2B4; hInstitute of Experimental Hematology, Hannover Medical School, 30625 Hannover, Germany; iDepartment of Physiology, McGill University, Montreal, QC, Canada H3A 2B4; jDFG Research Center for Regenerative Therapies, Technische Universität Dresden, 01307 Dresden, Germany; kMedical Faculty, Department of Anatomy and Molecular Embryology, Ruhr-University Bochum, 44801 Bochum, Germany; and lMedicial Faculty, Westphalian Wilhelms-University of Muenster, 48149 Muenster, Germany Edited by Brigid L. M. Hogan, Duke University Medical Center, Durham, NC, and approved February 1, 2017 (received for review August 30, 2016) Rapid and efficient protocols to generate oligodendrocytes (OL) more, these protocols require long culture periods (70–150 d) to + from human induced pluripotent stem cells (iPSC) are currently obtain O4 OL and show limited efficiency (9–12). -
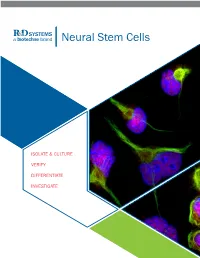
Neural Stem Cells
RnDSy-lu-2945 Neural Stem Cells ISOLATE & CULTURE VERIFY DIFFERENTIATE INVESTIGATE ISOLATE AND CULTURE Neural Stem cells (NSCs) require specialized media and growth factors to ensure efficient expansion. In addition to multipotent mouse and rat primary cortical stem cells, Bio-Techne offers a variety of serum-free neural media supplements, growth factors, and small molecules to maintain and expand NSCs. N21-MAX Cell Culture Supplements and Substrates • Improved Cell Health: high-quality culture reagents to ensure better growth and differentiation • Efficient Growth: optimized to enhance neural cell growth in culture Product Catalog # N-2 Plus Media Supplement AR003 N-2 MAX Media Supplement AR009 N21-MAX Media Supplement AR008 N21-MAX Insulin Free Media Supplement AR010 Competitor N21-MAX Vitamin A Free Media Supplement AR012 Holo-Transferrin 2914-HT Human Fibronectin, CF 1918-FN Bovine Fibronectin, CF 1030-FN Recombinant Human Fibronectin Full, CF 4305-FN Recombinant Human Fibronectin Fragment 2 3225-FN Recombinant Human Fibronectin Fragment 3 3938-FN Recombinant Human Fibronectin Fragment 4 3624-FN Recombinant Human Fibronectin, GMP 4305-GMP Recombinant Human Fibronectin, ACFP ACFP4305 Increased Synaptic Puncta and Neurite Outgrowth of ® Cultrex Poly-L-Lysine 3438-100-01 Primary Neurons Cultured in N21-MAX. E18 rat hippo- campal neurons were grown for 21 days in vitro in media supplemented with either N21-MAX Media Supplement (Catalog # AR008) or the neural media supplement from the most widely-used competitor. Staining for Synaptotagmin (yellow) showed more robust synaptic puncta and increased neurite outgrowth in neurons cultured in N21-MAX compared to those cultured in competitor media. Cells were stained with a Mouse Anti-Rat Synaptotagmin-1 Monoclonal Antibody (Catalog # MAB4364) followed by the NorthernLights™ (NL)557-conjugated Donkey Anti-Mouse IgG Secondary Antibody (Catalog # NL007). -

Stem Cells in Human Neurodegenerative Disorders — Time for Clinical Translation? Olle Lindvall1,2 and Zaal Kokaia2,3
Review series Stem cells in human neurodegenerative disorders — time for clinical translation? Olle Lindvall1,2 and Zaal Kokaia2,3 1Laboratory of Neurogenesis and Cell Therapy, Wallenberg Neuroscience Center, University Hospital, Lund, Sweden. 2Lund Stem Cell Center, Lund, Sweden. 3Laboratory of Neural Stem Cell Biology and Therapy, University Hospital, Lund, Sweden. Stem cell–based approaches have received much hype as potential treatments for neurodegenerative disorders. Indeed, transplantation of stem cells or their derivatives in animal models of neurodegenerative diseases can improve function by replacing the lost neurons and glial cells and by mediating remyelination, trophic actions, and modulation of inflammation. Endogenous neural stem cells are also potential therapeutic targets because they pro- duce neurons and glial cells in response to injury and could be affected by the degenerative process. As we discuss here, however, significant hurdles remain before these findings can be responsibly translated to novel therapies. In particular, we need to better understand the mechanisms of action of stem cells after transplantation and learn how to control stem cell proliferation, survival, migration, and differentiation in the pathological environment. Introduction patients need to be established, and all the associated ethical, Neurodegenerative disease is a term used for a wide range of regulatory, societal, and economical issues need to be addressed. acute and chronic conditions in which neurons and glial cells in Here, we discuss some general issues relating to the clinical trans- the brain and spinal cord are lost. In acute cases, for example, in lation of stem cells. We also describe how far stem cell–based response to ischemic stroke or spinal cord injury, different types approaches for treating some acute and chronic neurodegenera- of neurons and glial cells die within a restricted brain area over a tive disorders have advanced and define the critical milestones short time period. -

Alcohol, Neural Stem Cells, and Adult Neurogenesis
RESEARCH UPDATE ALCOHOL, NEURAL STEM CELLS, regions of the adult brain: (1) in the dentate gyrus of the hippocampus, a brain region important for learning and mem AND ADULT NEUROGENESIS ory, and (2) in the subventricular zone (SVZ) of the anterior lateral ventricles, the site of origin for olfactory bulb neurons. (See the sidebar “What Is a Stem Cell?” for more detailed Fulton T. Crews, Ph.D., and Kim Nixon, Ph.D. information about these cells and, in particular, the role of NSCs in the central nervous system.) The function of adult NSCs is not known, but they are associated with complicated Recent research demonstrates that neural stem cells brain functions such as learning, mood, and association of divide throughout life and give rise to new neurons, a sensory information. The discovery of NSCs and adult neuro process known as neurogenesis. This article addresses genesis provides a new theoretical framework for understand two principal questions concerning alcohol and adult ing processes regulating brain plasticity (Gage 2000). As neurogenesis: To what extent are neurogenesis in the addiction is thought to represent maladaptive changes in adult brain and the risk for alcoholism governed by brain plasticity, understanding the role of alcohol-induced similar factors? And, to what extent and through what changes in the brain and exploiting the new research find ings on brain plasticity should be included in scientists’ mechanisms do alcohol use and alcoholism affect adult schema for understanding, treating, and curing alcoholism. neurogenesis? This article also discusses genetic and This article addresses two principal questions concerning environmental influences on risk for alcoholism and on the connection between alcohol and adult neurogenesis. -

Developing Human Pluripotent Stem Cell-Based Cerebral Organoids
bioRxiv preprint doi: https://doi.org/10.1101/2020.10.09.331710; this version posted October 12, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. 1 Developing Human Pluripotent Stem Cell-Based Cerebral Organoids with a Controllable Microglia 2 Ratio for Modeling Brain Development and Pathology 3 4 Ranjie Xu1, *, Andrew J. Boreland1,5, Xiaoxi Li2, Caroline Erickson3, Mengmeng Jin1, Colm Atkins1, Zhiping 5 Pang4, Brian P. Daniels1, Peng Jiang1, * 6 7 1Department of Cell Biology and Neuroscience, Rutgers University, Piscataway, NJ 08854, USA. 8 2Department of Immunology, Nanjing Medical University, Nanjing, China. 9 3Summer Undergraduate Research Program in Neuroscience (NeuroSURP), Rutgers Robert Wood 10 Johnson Medical School, Piscataway, NJ 08854, USA 11 4Department of Neuroscience and Cell Biology and Child Health Institute of New Jersey, Rutgers Robert 12 Wood Johnson Medical School, New Brunswick, NJ 08901, USA 13 5Graduate Program in Molecular Biosciences, Rutgers University, Piscataway, NJ 08854, USA. 14 15 16 *Correspondence: [email protected] and [email protected] 17 18 19 20 21 22 23 24 1 bioRxiv preprint doi: https://doi.org/10.1101/2020.10.09.331710; this version posted October 12, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. -

The Cell Biology of Neurogenesis
REVIEWS THE CELL BIOLOGY OF NEUROGENESIS Magdalena Götz* and Wieland B. Huttner‡ Abstract | During the development of the mammalian central nervous system, neural stem cells and their derivative progenitor cells generate neurons by asymmetric and symmetric divisions. The proliferation versus differentiation of these cells and the type of division are closely linked to their epithelial characteristics, notably, their apical–basal polarity and cell-cycle length. Here, we discuss how these features change during development from neuroepithelial to radial glial cells, and how this transition affects cell fate and neurogenesis. DEVELOPMENTAL CELL BIOLOGY MACROGLIAL CELLS During development, neural stem cells give rise to These types of division were first deduced from retroviral Collective term for astrocytes, all the neurons of the mammalian central nervous cell-lineage-tracing experiments19–25 and were subse- oligodendrocytes and Schwann system (CNS). They are also the source of the two quently shown directly in live time-lapse observations cells. types of MACROGLIAL CELL in the CNS — ASTROCYTES and with brain slices26–31 and isolated cells in vitro32–37. OLIGODENDROCYTES1–5 ASTROCYTES . Usually, two criteria are applied to This review mainly discusses the cell-biological basis The main type of glial cell, define a cell as a stem cell — self-renewal, ideally for an of the symmetric versus asymmetric division of neural which has various supporting unlimited number of cell divisions, and multipotency, stem and PROGENITOR CELLS, concentrating on the devel- functions, including that is, the ability to give rise to numerous types of oping CNS of rodents (from which most of the available participating in the formation differentiated cell. -

Translating Neural Stem Cells to Neurons in the Mammalian Brain
Cell Death & Differentiation (2019) 26:2495–2512 https://doi.org/10.1038/s41418-019-0411-9 REVIEW ARTICLE Translating neural stem cells to neurons in the mammalian brain 1,2 1,2,3 1,2,3,4 Siraj K. Zahr ● David R. Kaplan ● Freda D. Miller Received: 28 April 2019 / Revised: 5 July 2019 / Accepted: 8 August 2019 / Published online: 24 September 2019 © The Author(s), under exclusive licence to ADMC Associazione Differenziamento e Morte Cellulare 2019 Abstract The mammalian neocortex underlies our perception of sensory information, performance of motor activities, and higher- order cognition. During mammalian embryogenesis, radial glial precursor cells sequentially give rise to diverse populations of excitatory cortical neurons, followed by astrocytes and oligodendrocytes. A subpopulation of these embryonic neural precursors persists into adulthood as neural stem cells, which give rise to inhibitory interneurons and glia. Although the intrinsic mechanisms instructing the genesis of these distinct progeny have been well-studied, most work to date has focused on transcriptional, epigenetic, and cell-cycle control. Recent studies, however, have shown that posttranscriptional mechanisms also regulate the cell fate choices of transcriptionally primed neural precursors during cortical development. These mechanisms are mediated primarily by RNA-binding proteins and microRNAs that coordinately regulate mRNA translation, stability, splicing, and localization. Together, these findings point to an extensive network of posttranscriptional 1234567890();,: 1234567890();,: control and provide insight into both normal cortical development and disease. They also add another layer of complexity to brain development and raise important biological questions for future investigation. Facts mRNA translation to regulate self-renewal versus differentiation. ● Numerous posttranscriptional regulators including RBPs and miRNAs are expressed in a temporally dynamic and cell-type specific manner during embryonic corticogenesis. -

Human Neuroepithelial Stem Cell Regional Specificity Enables Spinal Cord Repair Through a Relay Circuit
ARTICLE DOI: 10.1038/s41467-018-05844-8 OPEN Human neuroepithelial stem cell regional specificity enables spinal cord repair through a relay circuit Maria Teresa Dell’Anno1,2, Xingxing Wang 1,2, Marco Onorati 3,4, Mingfeng Li4, Francesca Talpo4, Yuichi Sekine 1,2, Shaojie Ma 4, Fuchen Liu 4, William B.J. Cafferty 2, Nenad Sestan 1,4,5 & Stephen M. Strittmatter 1,2,4 Traumatic spinal cord injury results in persistent disability due to disconnection of surviving 1234567890():,; neural elements. Neural stem cell transplantation has been proposed as a therapeutic option, but optimal cell type and mechanistic aspects remain poorly defined. Here, we describe robust engraftment into lesioned immunodeficient mice of human neuroepithelial stem cells derived from the developing spinal cord and maintained in self-renewing adherent conditions for long periods. Extensive elongation of both graft and host axons occurs. Improved functional recovery after transplantation depends on neural relay function through the grafted neurons, requires the matching of neural identity to the anatomical site of injury, and is accompanied by expression of specific marker proteins. Thus, human neuroepithelial stem cells may provide an anatomically specific relay function for spinal cord injury recovery. 1 Cellular Neuroscience, Neurodegeneration and Repair (CNNR) Program, Yale School of Medicine, New Haven, CT 06536, USA. 2 Department of Neurology, Yale School of Medicine, New Haven, CT 06520, USA. 3 Unit of Cell and Developmental Biology, Department of Biology, University of Pisa, Pisa 56127, Italy. 4 Department of Neuroscience, Yale School of Medicine, New Haven, CT 06520, USA. 5 Department of Genetics, of Psychiatry and of Comparative Medicine, and Yale Child Study Center, Yale School of Medicine, New Haven, CT 06510, USA. -

Notch Regulates the Switch from Symmetric to Asymmetric Neural Stem Cell Division in the Drosophila Optic Lobe Boris Egger, Katrina S
DEVELOPMENT AND STEM CELLS RESEARCH ARTICLE 2981 Development 137, 2981-2987 (2010) doi:10.1242/dev.051250 © 2010. Published by The Company of Biologists Ltd Notch regulates the switch from symmetric to asymmetric neural stem cell division in the Drosophila optic lobe Boris Egger, Katrina S. Gold and Andrea H. Brand* SUMMARY The proper balance between symmetric and asymmetric stem cell division is crucial both to maintain a population of stem cells and to prevent tumorous overgrowth. Neural stem cells in the Drosophila optic lobe originate within a polarised neuroepithelium, where they divide symmetrically. Neuroepithelial cells are transformed into asymmetrically dividing neuroblasts in a precisely regulated fashion. This cell fate transition is highly reminiscent of the switch from neuroepithelial cells to radial glial cells in the developing mammalian cerebral cortex. To identify the molecules that mediate the transition, we microdissected neuroepithelial cells and compared their transcriptional profile with similarly obtained optic lobe neuroblasts. We find genes encoding members of the Notch pathway expressed in neuroepithelial cells. We show that Notch mutant clones are extruded from the neuroepithelium and undergo premature neurogenesis. A wave of proneural gene expression is thought to regulate the timing of the transition from neuroepithelium to neuroblast. We show that the proneural wave transiently suppresses Notch activity in neuroepithelial cells, and that inhibition of Notch triggers the switch from symmetric, proliferative division, to asymmetric, differentiative division. KEY WORDS: Neural stem cells, Notch, Drosophila, Optic lobe, Proneural factor INTRODUCTION symmetric to asymmetric neural stem cell division. The optic Neurons must be generated in a precisely timed fashion to build lobe is the visual processing centre of the brain. -
Neural Stem Cell Markers
Neural Stem Cell Markers Neural Stem Cell Markers Neural Stem Cells Neural stem cells (NSCs) offer a unique The neurons communicate via synapses is to form the insulating myelin sheaths and powerful tool for basic research and and fall into different functional categories around axons in the CNS. Furthermore, regenerative medicine. Changes in the based on their neurochemical properties. oligodendrocytes provide trophic support expression levels of specific molecules to neurons by the production of different help to identify the presence of neural Astrocytes growth factors like BDNF and GDNF. stem cells in studies focused on further Astrocytes constitute the main glial differentiation toward specific neural cell population in the central nervous See tables 1-4 for a list of selected NSC lineages. system. These cells are derived from markers available from Atlas Antibodies. heterogeneous populations of progenitor cells in the neuroepithelium of the Commonly used markers for neural stem Related Publications developing central nervous system. cells include Nestin and SOX2. Other Bond AM. (2015) Adult Mammalian Neural Stem Cells protein markers, expressed at the cell and Neurogenesis: Five Decades Later. Cell Stem Cell. Astrocytes play a number of active roles 1;17(4):385-95 surface are, for example, ABCG2, FGFR1 in the brain, including the secretion or and Frizzled-9. Casarosa S. et al. (2014) Neural stem cells: ready for therapeutic absorption of neural transmitters, ion applications? Mol Cell Ther. 2: 31 homeostasis and maintenance of the Neurons Gage FH.,Temple S. (2013) Neural Stem Cells: Generating blood–brain barrier. and Regenerating the Brain. Neuron 80 (3):588-601 The neurons (nerve cells) are electrically excitable cells that transmit and relay the Jessell TM.