DOCSLIB.ORG

A Family of Subgraphs of Fibonacci Cubes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Family of Subgraphs of Fibonacci Cubes August 30, 2020 12:9 112-IJFCS 2050031 International Journal of Foundations of Computer Science Vol. 31, No. 5 (2020) 639{661 c World Scientific Publishing Company DOI: 10.1142/S0129054120500318 k-Fibonacci Cubes: A Family of Subgraphs of Fibonacci Cubes Omer¨ E˘gecio˘glu∗ Department of Computer Science University of California Santa Barbara Santa Barbara, California 93106, USA [email protected] Elif Saygı Department of Mathematics and Science Education Hacettepe University, Ankara 06800, Turkey [email protected] Z¨ulf¨ukar Saygı Department of Mathematics TOBB University of Economics and Technology Ankara 06560, Turkey [email protected] Received 29 November 2019 Accepted 19 February 2020 Published 26 August 2020 Communicated by Oscar Ibarra Hypercubes and Fibonacci cubes are classical models for interconnection networks with interesting graph theoretic properties. We consider k-Fibonacci cubes, which we obtain as subgraphs of Fibonacci cubes by eliminating certain edges during the fundamental recursion phase of their construction. These graphs have the same number of vertices as Fibonacci cubes, but their edge sets are determined by a parameter k. We obtain properties of k-Fibonacci cubes including the number of edges, the average degree of a vertex, the degree sequence and the number of hypercubes they contain. Keywords: Hypercube; Fibonacci cube; Fibonacci number. 1. Introduction An interconnection network can be represented by a graph G = (V; E) with ver- tex set V denoting the processors and edge set E denoting the communication links between the processors. One of the basic models for these networks is the n- dimensional hypercube graph Qn, whose vertices are indexed by all binary strings ∗Corresponding author. 639 August 30, 2020 12:9 112-IJFCS 2050031 640 O.¨ E˘gecio˘glu,E. Saygı & Z. Saygı of length n and two vertices are adjacent if and only if their Hamming distance is 1. Hsu [4], defined the n-dimensional Fibonacci cubes Γn as an alternative model of computation for interconnection networks and showed that they have interest- ing properties. Γn is a subgraph of Qn, where the vertices are those without two consecutive 1's in their binary string representation. Γ0 is defined as Q0, the graph with a single vertex and no edges. Numerous graph theoretic properties of Fibonacci cubes have been studied. In [8], a survey of the some of the properties including representations, recursive con- struction, hamiltonicity, degree sequences and other enumeration results are given. The induced d-dimensional hypercubes Qd in Γn are studied in [3, 9, 12, 13, 16, 17] and the boundary enumerator polynomial of hypercubes in Γn is considered in [18]. The number of vertex and edge orbits of Fibonacci cubes are determined in [1]. A Fibonacci string of length n which indexes the vertices of Γn is a binary string b b : : : b such that b b = 0 for 1 i n 1. The additional requirement 1 2 n i · i+1 ≤ ≤ − b b = 0 for n 2 defines a subgraph of Γ called Lucas cube Λ , which was also 1 · n ≥ n n proposed as a model for interconnection networks [14]. Other classes of graphs have also been defined along the lines of Fibonacci cubes. For instance subgraphs of Qn where k consecutive 1's are forbidden are proposed in [5] and Fibonacci (p; r)-cubes are presented in [2]. The generalized Fibonacci cube Qn(f) is defined as the subgraph of Qn by removing all the vertices that contain some forbidden string f [6]. With this formulation one has Γn = Qn(11). In this paper, we consider a special subgraph of Γn which is obtained by elim- inating certain edges. These are called k-Fibonacci cubes (or k-Fibonacci graphs) k and denoted by Γn as they depend on a parameter k. The edge elimination which defines k-Fibonacci cubes is carried out at the step analogous to where the funda- mental recursion is used to construct Γn from the two previous cubes by link edges. k The eliminated edges in Γn then recursively propagate according to the resulting fundamental construction which now depend on the value of the parameter k. k We obtain properties of Γn including the number of edges, the average degree of a vertex, the degree sequence and the number of hypercubes they contain. 2. Preliminaries Fibonacci numbers are defined by the recursion fn = fn 1 + fn 2 for n 2, with − − ≥ f0 = 0 and f1 = 1. Similarly, the Lucas numbers Ln are defined by the recursion Ln = Ln 1 + Ln 2 for n 2, with L0 = 2 and L1 = 1. Any positive integer − − ≥ can be uniquely represented as a sum of non-consecutive Fibonacci numbers. This representation is usually called the Zeckendorf or canonical representation. Here we note that this representation corresponds to the Fibonacci strings. For some positive n integer i assume that 0 i fn+2 1. Then i can be written as i = bj fn j+2, ≤ ≤ − j=1 · − where b 0; 1 . This gives that the Zeckendorf representation of i is (b ; b ; : : : ; b ) j 2 f g P 1 2 n and it corresponds to the Fibonacci string b1b2 : : : bn. Note that here we assume the integer 0 has Zeckendorf representation (0; 0;:::; 0). As an example, for n = 4, August 30, 2020 12:9 112-IJFCS 2050031 February 18, 2020 22:15 WSPC/INSTRUCTION FILE k-Fibonacci˙Cubes˙Egecioglu˙Saygi˙Feb19˙2020˙revised˙revised k-Fibonacci Cubes: A Special Family of Subgraphs of Fibonacci Cubes 641 7 = 5 + 2 = 1 f + 0 f + 1 f + 0 f gives that the Zeckendorf representation of · 5 · 4 · 3 · 2 7 is (1; 0; 1; 0) and this corresponds to the Fibonacci string 1010. The distance betweenk-Fibonacci two vertices cubes: Au specialand v familyin a connected of subgraphs graph of FibonacciG is defined cubes 3 as the length of a shortest path between u and v in G. For Qn and Γn this distance dimensionalcoincides with hypercube. the Hamming Then its distance vertex set (dH and) which edge is set the can number be written of different as bits in the string representation of the vertices. Let Qn = (V (Qn);E(Qn)) be the n- V (Q ) = 0, 1 n = b b . b b 0, 1 , 1 i n dimensional hypercube.n { Then} its{ vertex1 2 setn | andi ∈ edge { set} can≤ be≤ written} as E(Qn) = u, v n u, v V (Qn) and dH (u, v) = 1 . V (Qn) ={{0; 1 } |= b1∈b2 : : : bn bi 0; 1 ; 1 } i n f g f j 2 f g ≤ ≤ g n n 1 Of course V (Qn) = 2 and E(Qn) = n2 − . Similarly, we can write the vertex | E(Q| n) = u; v| u; v| V (Qn) and dH (u; v) = 1 : set and the edge set of Γffn = (Vg(Γ j n),E2(Γn)) as g n n 1 Of course V (Q ) = 2 and E(Q ) = n2 − . Similarly, we can write the vertex j n j j n j set and theV (Γ edgen) = setb1 ofb2 Γ. .= bn (Vb(Γi );E0, 1(Γ, ))1 asi n with bi bi+1 = 0 { n | ∈n { } n ≤ ≤ · } EV(Γ(Γn)) = = bu,b v : : :u, b v b V (Γ0n;)1 and; d1H (u,i v)n =with 1 . b b = 0 n {{f 1 2} | n j∈i 2 f g ≤ ≤ } i · i+1 g Note that theE(Γ number) = u; of v verticesu; v ofV the(Γ Fibonacci) and d ( cubeu; v) =Γn 1is: fn+2. n ff g j 2 n H g The fundamental decomposition [8] of Γn can be described as follows: Γn can Note that the number of vertices of the Fibonacci cube Γ is f . be decomposed into the subgraphs induced by the vertices thatn startn+2 with 0 and 10 The fundamental decomposition [8] of Γn can be described as follows: Γn can respectively. The vertices that start with 0 constitute a graph isomorphic to Γn 1 be decomposed into the subgraphs induced by the vertices that start with 0 and− 10 and the vertices that start with 10 constitute a graph isomorphic to Γn 2. This respectively. The vertices that start with 0 constitute a graph isomorphic− to Γn 1 decomposition can be written symbolically as − and the vertices that start with 10 constitute a graph isomorphic to Γn 2. This − decomposition can be writtenΓn symbolically= 0Γn 1 + 10Γ as n 2 . − − Γn = 0Γn 1 + 10Γn 2: In this representation the vertices are labeled− with− the Fibonacci strings. In Figure 1In the this first representation, six Fibonacci cubes the vertices are presented. are labeled The with labeling the Fibonacci of the vertices strings. follows In Fig. the 1 fundamentalthe first six recursion. Fibonacci For cubesn are2, presented. Γn is built The from labeling Γn 1 and of the Γn vertices2 by identifying follows the ≥ − − Γnfundamental2 with theΓ recursion.n 2 in Γn For1 byn what2, Γwen canis built call fromlink edges. Γn 1 Theand labels Γn 2 by of Γ identifyingn 1 stay − − − ≥ − − − unchangedΓn 2 with in the Γn Γ.n The2 in labels Γn 1 ofby the what vertices we can in call Γn link2 (whichedges. are The circled labels in of Figure Γn 1 stay 1) − − − − − areunchanged shifted up in by Γnf.n The+1 in labels Γn. of the vertices in Γn 2 (which are circled in Fig. 1) are − shifted up by fn+1 in Γn. Fig. 1. Fibonacci cubes Γ0; Γ1;:::; Γ5. Fig. 1. Fibonacci cubes Γ0, Γ1,..., Γ5. Throughout the paper we use the Fibonacci string representation and integer representation of the vertices interchangeably. For example, the first 8 vertices of Γ5 August 30, 2020 12:9 112-IJFCS 2050031 642 O.¨ E˘gecio˘glu,E.
Load more

Recommended publications
  • The Observability of the Fibonacci and the Lucas Cubes
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Discrete Mathematics 255 (2002) 55–63 www.elsevier.com/locate/disc The observability of the Fibonacci and the Lucas cubes Ernesto DedÃo∗;1, Damiano Torri1, Norma Zagaglia Salvi1 Dipartimento di Matematica, Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133 Milano, Italy Received 5 April 1999; received inrevised form 31 July 2000; accepted 8 January2001 Abstract The Fibonacci cube n is the graph whose vertices are binary strings of length n without two consecutive 1’s and two vertices are adjacent when their Hamming distance is exactly 1. If the binary strings do not contain two consecutive 1’s nora1intheÿrst and in the last position, we obtainthe Lucas cube Ln. We prove that the observability of n and Ln is n, where the observability of a graph G is the minimum number of colors to be assigned to the edges of G so that the coloring is proper and the vertices are distinguished by their color sets. c 2002 Elsevier Science B.V. All rights reserved. MSC: 05C15; 05A15 Keywords: Fibonacci cube; Fibonacci number; Lucas number; Observability 1. Introduction A Fibonacci string of order n is a binary string of length n without two con- secutive ones. Let and ÿ be binary strings; then ÿ denotes the string obtained by concatenating and ÿ. More generally, if S is a set of strings, then Sÿ = {ÿ: ∈ S}. If Cn denotes the set of the Fibonacci strings of order n, then Cn+2 =0Cn+1 +10Cn and |Cn| = Fn, where Fn is the nth Fibonacci number.
    [Show full text]
  • On Hardy's Apology Numbers
    ON HARDY’S APOLOGY NUMBERS HENK KOPPELAAR AND PEYMAN NASEHPOUR Abstract. Twelve well known ‘Recreational’ numbers are generalized and classified in three generalized types Hardy, Dudeney, and Wells. A novel proof method to limit the search for the numbers is exemplified for each of the types. Combinatorial operators are defined to ease programming the search. 0. Introduction “Recreational Mathematics” is a broad term that covers many different areas including games, puzzles, magic, art, and more [31]. Some may have the impres- sion that topics discussed in recreational mathematics in general and recreational number theory, in particular, are only for entertainment and may not have an ap- plication in mathematics, engineering, or science. As for the mathematics, even the simplest operation in this paper, i.e. the sum of digits function, has application outside number theory in the domain of combinatorics [13, 26, 27, 28, 34] and in a seemingly unrelated mathematical knowledge domain: topology [21, 23, 15]. Pa- pers about generalizations of the sum of digits function are discussed by Stolarsky [38]. It also is a surprise to see that another topic of this paper, i.e. Armstrong numbers, has applications in “data security” [16]. In number theory, functions are usually non-continuous. This inhibits solving equations, for instance, by application of the contraction mapping principle because the latter is normally for continuous functions. Based on this argument, questions about solving number-theoretic equations ramify to the following: (1) Are there any solutions to an equation? (2) If there are any solutions to an equation, then are finitely many solutions? (3) Can all solutions be found in theory? (4) Can one in practice compute a full list of solutions? arXiv:2008.08187v1 [math.NT] 18 Aug 2020 The main purpose of this paper is to investigate these constructive (or algorith- mic) problems by the fixed points of some special functions of the form f : N N.
    [Show full text]
  • Figurate Numbers
    Figurate Numbers by George Jelliss June 2008 with additions November 2008 Visualisation of Numbers The visual representation of the number of elements in a set by an array of small counters or other standard tally marks is still seen in the symbols on dominoes or playing cards, and in Roman numerals. The word "calculus" originally meant a small pebble used to calculate. Bear with me while we begin with a few elementary observations. Any number, n greater than 1, can be represented by a linear arrangement of n counters. The cases of 1 or 0 counters can be regarded as trivial or degenerate linear arrangements. The counters that make up a number m can alternatively be grouped in pairs instead of ones, and we find there are two cases, m = 2.n or 2.n + 1 (where the dot denotes multiplication). Numbers of these two forms are of course known as even and odd respectively. An even number is the sum of two equal numbers, n+n = 2.n. An odd number is the sum of two successive numbers 2.n + 1 = n + (n+1). The even and odd numbers alternate. Figure 1. Representation of numbers by rows of counters, and of even and odd numbers by various, mainly symmetric, formations. The right-angled (L-shaped) formation of the odd numbers is known as a gnomon. These do not of course exhaust the possibilities. 1 2 3 4 5 6 7 8 9 n 2 4 6 8 10 12 14 2.n 1 3 5 7 9 11 13 15 2.n + 1 Triples, Quadruples and Other Forms Generalising the divison into even and odd numbers, the counters making up a number can of course also be grouped in threes or fours or indeed any nonzero number k.
    [Show full text]
  • Fibonacci's Perfect Spiral
    Middle School Fibonacci's Perfect Spiral This l esson was created to combine math history, math, critical thinking, and art. Students will l earn about Fibonacci, the code he created, and how the Fibonacci sequence relates to real l ife and the perfect spiral. Students will practice drawing perfect spirals and l earn how patterns are a mathematical concept that surrounds us i n real l ife. This l esson i s designed to take 3 to 4 class periods of 45 minutes each, depending on the students’ focus and depth of detail i n the assignments. Common Core CCSS.MATH.CONTENT.HSF.IF.A.3 Recognize that Standards: sequences are functions, sometimes defined recursively, whose domain i s a subset of the i ntegers. For example, the Fibonacci sequence i s defined recursively by f(0) = f(1) = 1, f(n+1) = f(n) + f(n­1) for n ≥ 1. CCSS.MATH.CONTENT.7.EE.B.4 Use variables to represent quantities i n a real­world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities. CCSS.MATH.CONTENT.7.G.A.1 Solve problems involving scale drawings of geometric figures, i ncluding computing actual l engths and areas from a scale drawing and reproducing a scale drawing at a different scale. CCSS.MATH.CONTENT.7.G.A.2 Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. CCSS.MATH.CONTENT.8.G.A.2 Understand that a two­dimensional figure i s congruent to another i f the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
    [Show full text]
  • Student Task Statements (8.7.B.3)
    GRADE 8 MATHEMATICS BY NAME DATE PERIOD Unit 7, Lesson 3: Powers of Powers of 10 Let's look at powers of powers of 10. 3.1: Big Cube What is the volume of a giant cube that measures 10,000 km on each side? 3.2: Taking Powers of Powers of 10 1. a. Complete the table to explore patterns in the exponents when raising a power of 10 to a power. You may skip a single box in the table, but if you do, be prepared to explain why you skipped it. expression expanded single power of 10 b. If you chose to skip one entry in the table, which entry did you skip? Why? 2. Use the patterns you found in the table to rewrite as an equivalent expression with a single exponent, like . GRADE 8 MATHEMATICS BY NAME DATE PERIOD 3. If you took the amount of oil consumed in 2 months in 2013 worldwide, you could make a cube of oil that measures meters on each side. How many cubic meters of oil is this? Do you think this would be enough to fill a pond, a lake, or an ocean? 3.3: How Do the Rules Work? Andre and Elena want to write with a single exponent. • Andre says, “When you multiply powers with the same base, it just means you add the exponents, so .” • Elena says, “ is multiplied by itself 3 times, so .” Do you agree with either of them? Explain your reasoning. Are you ready for more? . How many other whole numbers can you raise to a power and get 4,096? Explain or show your reasoning.
    [Show full text]
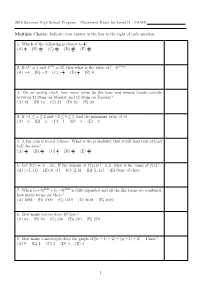
  • 2018 Summer High School Program Placement Exam for Level B NAME
    2018 Summer High School Program Placement Exam for Level B NAME: Multiple Choice: Indicate your answer in the box to the right of each question. 1 1. Which of the following is closest to 2 ? 2 7 9 10 23 (A) 3 (B) 13 (C) 19 (D) 21 (E) 48 2. If 42x = 4 and 4−5y = 32, then what is the value of (−4)x−y? 1 1 (A) −4 (B) −2 (C) − 4 (D) 4 (E) 4 3. On an analog clock, how many times do the hour and minute hands coincide between 11:30am on Monday and 11:30am on Tuesday? (A) 12 (B) 13 (C) 22 (D) 23 (E) 24 4. If −1 ≤ a ≤ 2 and −2 ≤ b ≤ 3, find the minimum value of ab. (A) −6 (B) −5 (C) −4 (D) −3 (E) −2 5. A fair coin is tossed 5 times. What is the probability that it will land tails at least half the time? 3 5 1 11 13 (A) 16 (B) 16 (C) 2 (D) 16 (E) 16 6. Let f(x) = j5 − 2xj. If the domain of f(x) is (−3; 3], what is the range of f(x)? (A) [−1; 11) (B) [0; 11) (C) [2; 8) (D) [1; 11) (E) None of these 7. When (a+b)2018 +(a−b)2018 is fully expanded and all the like terms are combined, how many terms are there? (A) 1008 (B) 1009 (C) 1010 (D) 2018 (E) 2019 8. How many factors does 10! have? (A) 64 (B) 80 (C) 120 (D) 240 (E) 270 9.
    [Show full text]
  • Solve the Rubik's Cube Using Proc
    Solve the Rubik’s Cube using Proc IML Jeremy Hamm Cancer Surveillance & Outcomes (CSO) Population Oncology BC Cancer Agency Overview Rubik’s Cube basics Translating the cube into linear algebra Steps to solving the cube using proc IML Proc IML examples The Rubik’s Cube 3x3x3 cube invented in 1974 by Hungarian Erno Rubik – Most popular in the 80’s – Still has popularity with speed-cubers 43x1018 permutations of the Rubik’s Cube – Quintillion Interested in discovering moves that lead to permutations of interest – or generalized permutations Generalized permutations can help solve the puzzle The Rubik’s Cube Made up of Edges and corners Pieces can permute – Squares called facets Edges can flip Corners can rotate Rubik’s Cube Basics Each move can be defined as a combination of Basic Movement Generators – each face rotated a quarter turn clockwise Eg. – Movement of front face ¼ turn clockwise is labeled as move F – ¼ turn counter clockwise is F-1 – 2 quarter turns would be F*F or F2 Relation to Linear Algebra The Rubik’s cube can represented by a Vector, numbering each facet 1-48 (excl centres). Permutations occur through matrix algebra where the basic movements are represented by Matrices Ax=b Relation to Linear Algebra Certain facets are connected and will always move together Facets will always move in a predictable fashion – Can be written as: F= (17,19,24,22) (18,21,23,20) (6,25,43,16) (7,28,42,13) (8,30,41,11) Relation to Linear Algebra Therefore, if you can keep track of which numbers are edges and which are corners, you can use a program such as SAS to mathematically determine moves which are useful in solving the puzzle – Moves that only permute or flip a few pieces at a time such that it is easy to predict what will happen Useful Group Theory Notes: – All moves of the Rubik’s cube are cyclical where the order is the number of moves needed to return to the original Eg.
    [Show full text]
  • The Mathematical Beauty of Triangular Numbers
    2015 HAWAII UNIVERSITY INTERNATIONAL CONFERENCES S.T.E.A.M. & EDUCATION JUNE 13 - 15, 2015 ALA MOANA HOTEL, HONOLULU, HAWAII S.T.E.A.M & EDUCATION PUBLICATION: ISSN 2333-4916 (CD-ROM) ISSN 2333-4908 (ONLINE) THE MATHEMATICAL BEAUTY OF TRIANGULAR NUMBERS MULATU, LEMMA & ET AL SAVANNAH STATE UNIVERSITY, GEORGIA DEPARTMENT OF MATHEMATICS The Mathematical Beauty Of Triangular Numbers Mulatu Lemma, Jonathan Lambright and Brittany Epps Savannah State University Savannah, GA 31404 USA Hawaii University International Conference Abstract: The triangular numbers are formed by partial sum of the series 1+2+3+4+5+6+7….+n [2]. In other words, triangular numbers are those counting numbers that can be written as Tn = 1+2+3+…+ n. So, T1= 1 T2= 1+2=3 T3= 1+2+3=6 T4= 1+2+3+4=10 T5= 1+2+3+4+5=15 T6= 1+2+3+4+5+6= 21 T7= 1+2+3+4+5+6+7= 28 T8= 1+2+3+4+5+6+7+8= 36 T9=1+2+3+4+5+6+7+8+9=45 T10 =1+2+3+4+5+6+7+8+9+10=55 In this paper we investigate some important properties of triangular numbers. Some important results dealing with the mathematical concept of triangular numbers will be proved. We try our best to give short and readable proofs. Most of the results are supplemented with examples. Key Words: Triangular numbers , Perfect square, Pascal Triangles, and perfect numbers. 1. Introduction : The sequence 1, 3, 6, 10, 15, …, n(n + 1)/2, … shows up in many places of mathematics[1] .
    [Show full text]
  • Florentin Smarandache
    FLORENTIN SMARANDACHE SEQUENCES OF NUMBERS INVOLVED IN UNSOLVED PROBLEMS 1 141 1 1 1 8 1 1 8 40 8 1 1 8 1 1 1 1 12 1 1 12 108 12 1 1 12 108 540 108 12 1 1 12 108 12 1 1 12 1 1 1 1 16 1 1 16 208 16 1 1 16 208 1872 208 16 1 1 16 208 1872 9360 1872 208 16 1 1 16 208 1872 208 16 1 1 16 208 16 1 1 16 1 1 2006 Introduction Over 300 sequences and many unsolved problems and conjectures related to them are presented herein. These notions, definitions, unsolved problems, questions, theorems corollaries, formulae, conjectures, examples, mathematical criteria, etc. ( on integer sequences, numbers, quotients, residues, exponents, sieves, pseudo-primes/squares/cubes/factorials, almost primes, mobile periodicals, functions, tables, prime/square/factorial bases, generalized factorials, generalized palindromes, etc. ) have been extracted from the Archives of American Mathematics (University of Texas at Austin) and Arizona State University (Tempe): "The Florentin Smarandache papers" special collections, University of Craiova Library, and Arhivele Statului (Filiala Vâlcea, Romania). It is based on the old article “Properties of Numbers” (1975), updated many times. Special thanks to C. Dumitrescu & V. Seleacu from the University of Craiova (see their edited book "Some Notions and Questions in Number Theory", Erhus Univ. Press, Glendale, 1994), M. Perez, J. Castillo, M. Bencze, L. Tutescu, E, Burton who helped in collecting and editing this material. The Author 1 Sequences of Numbers Involved in Unsolved Problems Here it is a long list of sequences, functions, unsolved problems, conjectures, theorems, relationships, operations, etc.
    [Show full text]
  • The TI-30X IIS Calculator and Exponents
    The TI-30X IIS Calculator and Exponents 2nd ARROWS ^ 2 x PARENTHESIS Squaring a number can be done easily using a x2 key. Cubing a number or raising it to any power can be achieved by using ^ key followed by number 3. Ø Squaring: input the number and then x2 =, 42 is found by inputting: 4 x2 = You screen will look like: 42 16 ➢ Cubing or raising a number to the third power: input the number and then ^3 =, 43 is found by inputting: 4 ^3 = You screen will look like: 4^3 64 ➢ Raising a number to a power greater than 3: input the number and then ^ (the power desired) =, (-3)4 is found by inputting: ( (-)3 ) ^ 4 = You screen will look like: (-3)^4 81 Note: if you did not put the -3 in parentheses, the orders of operation raises the 3 to the fourth power and then makes it negative, hence the answer will be -81. Be careful that you always put negative numbers in parentheses when raising them to powers. ➢ You can also take values to fractional exponents: 82/3 can be found by inputting: 8 ^ (2 ÷3) = You screen will look like: 8 ^ (2 / 3) 4 Taking a root can be done easily using √ option, which is achieved by pressing 2nd x2. Any other root (n-root), can be calculated by pressing (the root desired) 2nd ^. 2 ➢ Square root: √ the number =, is found by inputting: 2nd x 36 = You screen will look like: √(36 6 ➢ Cube root: ∛the number =, is found by inputting: 3 2nd ^ 64 = You screen will look like: 3 x√64 4 ➢ Taking a root higher than a cube root: (the root desired) 2nd ^ (the value) =, is found by inputting: 4 2nd ^ 1296 = You screen will look like: 4 x√1296 6 Since the root symbol works like a grouping symbol, there is no need to use parentheses for negative values.
    [Show full text]
  • Noncrossing Partitions Rodica Simion ∗ Department of Mathematics, the George Washington University, Washington, DC 20052, USA
    View metadata, citation and similar papers at core.ac.ukDiscrete Mathematics 217 (2000) 367–409 brought to you by CORE www.elsevier.com/locate/disc provided by Elsevier - Publisher Connector Noncrossing partitions Rodica Simion ∗ Department of Mathematics, The George Washington University, Washington, DC 20052, USA Received 8 September 1998; revised 5 November 1998; accepted 11 June 1999 Abstract In a 1972 paper, Germain Kreweras investigated noncrossing partitions under the reÿnement order relation. His paper set the stage both for a wealth of further enumerative results, and for new connections between noncrossing partitions, the combinatorics of partially ordered sets, and algebraic combinatorics. Without attempting to give an exhaustive account, this article illustrates aspects of enumerative and algebraic combinatorics supported by the lattice of noncrossing par- titions, re ecting developments since Germain Kreweras’ paper. The sample of topics includes instances when noncrossing partitions arise in the context of algebraic combinatorics, geometric combinatorics, in relation to topological problems, questions in probability theory and mathe- matical biology. c 2000 Elsevier Science B.V. All rights reserved. RÃesumÃe Dans un article paru en 1972, Germain Kreweras ÿt uneetude à des partitions noncroisÃees en tant qu’ensemble ordonnÃe. Cet article crÃea le cadre ou, depuis lors, on a dÃeveloppÃe une multitude de rÃesultats supplÃementaires ainsi que des nouveaux liens entre les partitions noncroisÃees, la combinatoire des ensembles ordonnÃes et la combinatoire algÃebrique. Sans ta ˆcher d’en donner un traitement au complet, l’article prÃesent exempliÿe quelques aspectsenumà à eratifs et de combi- natoire algÃebrique ou interviennent les partitions noncroisÃees. Ceux-ci mettent enevidence à des dÃeveloppements survenus depuis la publication de l’article de Germain Kreweras et qui portent sur des problÂemes en combinatoire algÃebrique et gÃeomÃetrique, ainsi que sur des questions reliÃees a la topologie, aux probabilitÃes eta  la biologie mathÃematique.
    [Show full text]
  • MTJPAM Lucas Cube Vs Zeckendorf's Lucas Code
    Montes Taurus J. Pure Appl. Math. 3 (2), 47–50, 2021 MTJPAM ISSN: 2687-4814 Lucas Cube vs Zeckendorf’s Lucas Code Sadjia Abbad ID a, Hacene` Belbachir ID b, Ryma Ould-Mohamed ID c aUSTHB, Faculty of Mathematics, RECITS Laboratory, BP 32 El-Alia, Bab-Ezzouar 16111, Algiers, Algeria. Saad Dahlab University, BP 270, Route de Soumaa, Blida, Algeria bUSTHB, Faculty of Mathematics, RECITS Laboratory, BP 32 El-Alia, Bab-Ezzouar 16111, Algiers, Algeria cUSTHB, Faculty of Mathematics, RECITS Laboratory, BP 32 El-Alia, Bab-Ezzouar 16111, Algiers, Algeria. University of Algiers 1, 2 Rue Didouche Mourad, Alger Ctre 16000, Algiers, Algeria Abstract The theorem of Zeckendorf states that every positive integer n can be uniquely decomposed as a sum of non consecutive Lucas P numbers in the form n = i biLi, where bi 2 f0; 1g and satisfy b0b2 = 0. The Lucas string is a binary string that do not contain two consecutive 1’s in a circular way. In this note, we derive a bijection between the set of Zeckendorf’s Lucas codes and the set of vertices of the Lucas’ strings. Keywords: Fibonacci numbers, Lucas numbers, Fibonacci cube, Lucas cube 2010 MSC: 11B39, 05C99 1. Introduction The Fibonacci numbers (Fn)n≥0 given by F0 = 0; F1 = 1 and Fn+1 = Fn + Fn−1; n ≥ 1; constitute a basis element of the binary Fibonacci numeration system, see for instance [11]. Every integer 0 ≤ N < Fn+1 has a unique binary representation a2a3 ··· an, such that Xn N = aiFi; i=2 with ai 2 f0; 1g and aiai+1 = 0; for 2 ≤ i ≤ n − 1: The binary string a2 ··· an is called a Zeckendorf’s Fibonacci code.
    [Show full text]