DOCSLIB.ORG

Bibechana 18 (1) (2021) 149-158

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bibechana 18 (1) (2021) 149-158 BIBECHANA 18 (1) (2021) 149-158 BIBECHANA ISSN 2091-0762 (Print), 2382-5340 (Online) Journal homepage: http://nepjol.info/index.php/BIBECHANA Publisher: Department of Physics, Mahendra Morang A.M. Campus, TU, Biratnagar, Nepal Investigation on thermo-physical properties of liquid In-Tl alloy I. B. Bhandari1,2, N. Panthi1,3 , I. Koirala1* 1Central Department of Physics, Tribhuvan University, Kirtipur, Nepal 2Department of Applied Sciences, Purwanchal Campus, Tribhuvan University, Dharan, Nepal 3Department of Physics, Patan Multiple Campus, Tribhuvan University, Lalitpur, Nepal *E-mail: [email protected] Article Information: ABSTRACT Received: June 29, 2020 This research explores mixing behaviour of liquid In – Tl system through Accepted: August 8, 2020 thermodynamic and the structural properties on the basis of Complex Formation Model. The properties like surface tension and viscosity have been analyzed through simple statistical model and Moelwyn – Hughes equation. The Keywords: interaction parameters are found to be positive, concentration independent and Mixing properties temperature dependent. Theoretical results are in a good agreement with the Ordering energy corresponding literature data which support homo-coordinating tendency in the Complex formation model liquid In-Tl alloy. Segregation DOI: https://doi.org/10.3126/bibechana.v18i1.29531 This work is licensed under the Creative Commons CC BY-NC License. https://creativecommons.org/licenses/by-nc/4.0/ 1. Introduction Indium is also used in nuclear reactor control rod alloys, low pressure sodium lamps and alkaline Indium is a substance which is used in solder alloys batteries. Additions of indium to lead–tin bearings which are applied in electronics for assembling are utilized in piston type aircraft engines, high semiconductor chips to a base and hybrid integrated performance automobile engines and in turbo– circuits and to seal glass to metal in vacuum tubes. diesel truck engines. The addition of indium to gold Fusible indium alloys are used to bend thin walled dental alloys recuperates their mechanical tubes without wrinkling the wall or changing the properties and increases resistance to discoloring. original cross-section. These alloys are not only Small amount of indium is used to improve the used in fire control system, restraining links that machinability of gold alloys for jewelry [1].The hold alarm, water valve and door operating indium–thallium alloy is a classic type of shape mechanism but also used as temperature indicators memory alloy with a low melting temperature. It in situations where other methods of temperature has wide range of practical applications in the field measurements are impracticable and infeasible [1]. of metallurgy which includes the use in 149 I. B. Bhandari et al. / BIBECHANA 18 (1) (2021) 149-158 thermostats, hydraulic lines and electrical circuits total number of atoms is N = NA + NB. When [2]. Thallium alone is improper for direct use components A and B are amalgamated together to because of its properties of toxicity, unfavorable form a binary A-B solution, thermodynamic mechanical properties and significant tendency to properties are changed. The liquid alloy is oxidize. Thallium contains the most constant considered to be ternary mixture of three species; A atomic vibration so far experimented. This property atom, B atom and chemical complex AuBv, is also of Tl preceded it to be used in atomic clocks. called conformal solution. The number of free Thallium immediately forms alloys with most other atoms will be reduced due to compound formation metals. There is incomplete mutual insolubility in the melt. Now for n1g atoms of A, n2g atoms of with iron and limited solubility in the liquid state B and n3g atoms of AuBv, with copper, aluminum, zinc, arsenic, manganese 푛1 = 푥 − 푢푛3 and 푛2 = (1 − 푥) − 푣푛3 (1) and nickel. Gold, silver, cadmium and tin formulate simple eutectic point with thallium. Thallium also The total number of atoms after mixing can be forms binary alloys with antimony, barium, given as calcium, cerium, cobalt, germanium, lanthanum, 푛 = 푛1 + 푛2 + 푛3 = 1 − (푢 + 푣 − 1)푛3 (2) lithium, magnesium, strontium, tellurium, bismuth The free energy of mixing of the binary A-B and indium. The ternary alloys of thallium Tl–Pb– mixture can be written as [23], Bi, Tl–Al–Ag, In–Hg–Tl, Sn–Cd–Tl, Bi–Sn–Tl and ′ 퐺푀 = −푛3푔 + 퐺 (3) Bi–Cd–Tl are used as semiconductors in ceramic compounds. Thallium has good wear resistance Here,−푛3푔 stands for lowering of free energy due when it is used in bearing shafts. Thallium to compound formation, g is the formation energy containing alloys are frequently recommended for of complex. 퐺′ is the free energy of mixing of the bearings, electronics industry such as in solid state ternary mixture of A, B and AuBv. If the ternary rectifiers, electrical fuses and soldering materials mixture is an ideal solution, [1]. The study of In-Tl alloy is also useful to 푛 퐺′ = 푅푇 ∑ 푛 푙푛 ( 푖) (4) 푖 푛 investigate the corresponding higher order alloy through different approaches [3]. There is difficulty If the effects of differences in sizes of the various in studying the properties of alloys in liquid state constituents in the mixture cannot be ignored and due to lack of long range atomic order. Therefore, the interaction 휔푖푗 are small but not zero, the theoreticians have exercised different models to theory of regular solutions in the zeroth understand the properties of various binary liquid approximation [25] or the conformal solution alloys [4–22]. The different properties were studied approximation [26] is valid. For regular solution at fixed temperature of 723 K through different 푛 푛 푛 퐺′ = 푅푇 ∑ 푛 푙푛 ( 푖) + ∑ 휔 ( 푖 푗) (5) models. In present work, we have explored the 푖 푛 푖푗 푛 energetic of In – Tl alloy at a temperature of 723K This equation is concerned to conformal solution using complex formation model [23]. The approximation. Where 휔푖푗= 0 (for i = j) are termed outcomes are analyzed and compared with as the interaction energies and by definition are literature data [24] to explicate the accuracy of this independent of concentration, although they are method in thermodynamic and structural depended upon temperature and pressure. description of the presented binary system. Now the expression for free energy of mixing GM for the compound forming binary alloy is 2. Theory 푛 퐺 = −푛 푔 + 푅푇 ∑3 푛 푙푛 ( 푖) + Thermodynamic properties 푀 3 푖=1 푖 푛 푛푖푛푖 If a binary alloy contains NA = x number of A ∑ ∑ ( ) 휔 (6) 푖<푗 푛 푖푗 atoms and NB = (1-x) number of B atoms, so that 150 I. B. Bhandari et al. / BIBECHANA 18 (1) (2021) 149-158 The expression for heat of mixing HM is given of atomic order. The concentration fluctuation at by[23] long wavelength limit is related with free energy of 휕퐺푀 mixing by the expression [27], 퐻푀 = 퐺푀 − 푇 ( ) (7) 휕푇 푃 푅푇 푆푐푐(0) = 2 (13) Substituting for GM, 휕 퐺푀 2 3 휕푐 푛푖 퐻푀 = −푛3푔 + 푅푇 ∑ 푛푖푙푛 ( ) 푅푇 푛 ( ) 1 푆푐푐 0 = 2 (푛′) ′ 2 ′ 푛 ′ 푛 푛 3 푖 (푛 ) 푛푖 푗 푖 푗 푅푇 ∑푖=1( − )+2푛 ∑푖<푗 ∑ 휔푖푗( ) ( ) + ∑ ∑ ( ) 휔 푛푖 푛 푛 푛 푛 푖푗 푖<푗 (14) 3 휕 푛 Theoretically computed values of 푆푐푐(0) can be − 푇 [−푛 푔 + 푅푇 ∑ 푛 푙푛 ( 푖) 휕푇 3 푖 푛 compared with the observed values computed from 푖=1 activity data by the expression, −1 −1 푛푖푛푗 휕푎퐴 휕푎퐵 + ∑ ∑ ( ) 휔 ] 푆푐푐(0) = (1 − 푥)푎퐴 ( ) = 푥푎퐵 ( ) 푛 푖푗 휕푐 푇,푃,푁 휕푐 푇,푃,푁 푖<푗 (15) 휕푔 1 퐻푀 = −푛3 [푔 − 푇 ( ) ] + ∑푖<푗 ∑(푛푖푛푗) [휔푖푗 − The ideal value of Scc(0) can be expressed as, 휕푇 푃 푛 푆푖푑(0) = 푥(1 − 푥) (16) 휕휔푖푗 푐푐 푇 ( ) ] (8) 휕푇 푃 The Warren–Cowley short range order parameter The expression for entropy of mixing SM can be quantify the degree of local order in the binary obtained as [23] alloy [28,29]. The theoretical values of this 휕푔 3 푛푖 푛푖푛푗 휕휔푖푗 parameter can be calculated as 푆푀 = 푛3 − 푅 ∑푖=1 푛푖푙푛 − ∑푖<푗 ∑ 휕푇 푛 푛 휕푇 (s−1) Scc(0) α1 = ,S = id (17) (9) s(z−1)+1 Scc(0) The equilibrium value of 푛3 at a given pressure and where z is coordination number, which is taken as temperature is given by[23] 10 for our calculation. 휕퐺 ( 푀) = 0 (10) Transport Properties 휕푛 3 푇,푃,푁,퐶 Substituting the value of GM from Equation (6) and The mixing behaviour of the alloys forming molten after some algebraic calculation alloy can also be studied at the microscopic level in 푔 푙푛(푛 푛푢+푣−1푛−푢푛−푣) + 푌 = (11) terms of coefficient of diffusion. The mutual 3 1 2 푅푇 The Equation (11) is called equilibrium equation, diffusion coefficient (DM) of binary liquid alloys where can be expressed in terms of activity (ai) and self- 푛 푛 푛 푛 휔 diffusion coefficient (Did) of pure component with 푌 = [ 1 2 (푢 + 푣 − 1) − 푢 2 − 푣 1] 12 + 푛2 푛 푛 푅푇 the help of Darken’s equation [30] 푛2푛3 푛3 푛2 휔23 푑푙푛푎 [ (푢 + 푣 − 1) − 푣 + ] + 퐷 = 퐷 푥 푖 (18) 푛2 푛 푛 푅푇 푀 푖푑 푑푥 푛1푛3 푛3 푛1 휔13 [ (푢 + 푣 − 1) − 푢 + ] (12) with 퐷푀 = 푐퐴퐷퐵 + 푐퐵퐷퐴 푛2 푛 푛 푅푇 where DA and DB are the self – diffusion Structural Properties coefficients of pure components A and B The concentration fluctuation at long wavelength respectively, limit is of good interest because any deviation from The expression for DM in terms of Scc(0) can be 푖푑 given as ideal value 푆푐푐 (0) is significant in describing the 퐷 푆푖푑(0) nature of ordering and phase segregation in molten 푀 = 푐푐 (19) 퐷 푆 (0) alloys.
Load more

Recommended publications
  • Directorate of Agricultural Engineering (Moa) • Suppliers, Fabricators, Maintenance Shop & Custom Hiring Service Provider
    Country Presentation Nepal The 3rd Regional Forum on Sustainable Agricultural Mechanization Human Resource Development for Sustainable Agricultural Mechanization 9-11 December 2015 Manila, the Philippines Role of Academic and Research Institutions in Human Resource Development for Sustainable Agricultural Mechanization in Nepal Yam Kumar Rai Program Coordinator Department of Agricultural Engineering Purwanchal Campus, Dharan Nepal Outline of Presentation • Background • Agriculture Scenario of Nepal • Brief Introduction of Dept. of Agricultural Engineering • Need of Agricultural Mechanization in Nepal, its Challenges and opportunities • Role of Academic and Research Institutions, challenges and constraints • Role of stakeholders for sustainable agricultural mechanization • Suggestion for regional cooperation • Conclusions Background Total Area= 147,181 sq km ( EW 885 km, NS 193 km ) Altitude = 60 m to 8,848 m Total Populations = 26.5 M Population growth rate per annum = 1.35 % S.N. Region Total Land Area % Cultivated Land Area 1 Mountain 35 2.17 2 Hill 42 11.4 3 Terai 23 12.46 4 Total Area % 100 26.03 Agriculture Scenario of Nepal 7 6000000 Mounta in 6 Hill 5000000 5 Terai 4000000 4 Paddy 3 3000000 Area in in % Area Wheat 2 Maize 2000000 Production Ton) in(M. Production Millet 1 barley 1000000 0 Paddy Wheat Maize Millet barley Mountain 0.42 0.39 0.59 0.38 0.1 0 Hill 2.67 2.02 4.25 1.42 0.18 Terai 6.54 2.95 0.78 0.06 0.01 Area covered by main crops Years Agriculture Scenario of Nepal 4 3500000 3.5 3000000 3 2500000 2.5 2000000 Sugarcane 2 Mountain 1500000 Ton/ha Oil seed Hill Tobacco 1.5 Terai (M.
    [Show full text]
  • REVISED FIRST ADMISSION Listt 2074
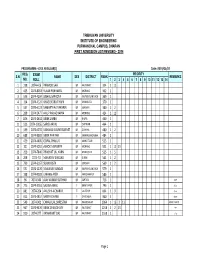
    TRIBHUVAN UNIVERSITY INSTITUTE OF ENGINEERING PURWANCHAL CAMPUS, DHARAN FIRST ADMISSION LIST(REVISED)- 2074 PROGRAMME:- CIVIL REGULAR(1) Date:-2074/05/07 REG. EXAM PRIORITY S.N. NAME SEX DISTRICT RANK REMARKS NO. ROLL 1 2 3 4 5 6 7 8 9 1011121314 1 238 2074-416 PRAMOD SAH M RAUTAHAT 334 1 11 2 403 2074-8263 RUJAN POKHAREL M MORANG 362 1 3 536 2074-4204 BISHAL SAPKOTA M KAVREPALANCHOK 369 1 4 114 2074-4124 KHAGENDRA THAPA M DHANKUTA 370 1 5 547 2074-4123 SAMARTHAK PAKHRIN M SUNSARI 380 1 2 6 208 2074-5477 ANUP RAJ ACHARYA M MORANG 424 1 11 7 826 2074-2632 BIBEK LIMBU M JHAPA 440 1 8 523 2074-10052 SAROJ ARYAL M CHITWAN 464 1 9 599 2074-4255 BISHWAS KUMAR BASNET M GORKHA 480 1 2 10 688 2074-9902 BIBEK PARIYAR M SANKHUWASABHA 484 1 11 429 2074-4405 GOPAL THAKUR M MAHOTTARI 513 1 12 101 2074-5092 ASHOK TAJPURIYA M MORANG 531 1 11 13 13 259 2074-7846 PRABHAT LAL KARN M DHANUSHA 535 1 5 14 258 2074-73 MAHADEV SINGJALI M GULMI 561 1 2 15 799 2074-6167 SURAJ BISTA M SUNSARI 569 1 2 16 531 2074-1270 NAWARAJ SUNDAS M KAVREPALANCHOK 579 1 17 198 2074-9283 UMANG AYER M KANCHANPUR 586 1 18 96 2074-340 AJAY KUMAR SUTIHAR M SAPTARI 716 1 dw];L 19 775 2074-3761 SALINA AWAL F BHAKTAPUR 746 1 dlxnf 20 881 2074-204 ANUSHA ACHARYA F LALITPUR 804 1 9 dlxnf 21 915 2074-4857 SABITA DHAMI F DARCHULA 960 1 dlxnf 22 549 2074-901 CHHABI LAL SHRESTHA M RAMECHHAP 1064 1 13 2 11 cflbjf;L hghftL 23 967 2074-9470 BIBEK CHAUDHARY M RAUTAHAT 1258 1 2 13 yf? 24 920 2074-277 RAMAKANT DAS M RAUTAHAT 1558 1 blnt Page 1 TRIBHUVAN UNIVERSITY INSTITUTE OF ENGINEERING PURWANCHAL CAMPUS, DHARAN FIRST ADMISSION LIST(REVISED)- 2074 PROGRAMME:- CIVIL FULL FEE(2) Date:-2074/05/07 REG.
    [Show full text]
  • Information Brochure
    Tribhuvan University Institute of Engineering Entrance Examination Board Information Brochure Entrance Examination and Admission Procedure for M.Sc. Programs under IOE IOE Entrance Examination Board-2074 2018(2074) Tribhuvan University Institute of Engineering Entrance Examination Board Detailed Schedule for Entrance Examination of Masters Programs – 2074 Time and Date for Online Application: From 10 AM, 1stFalgun 2073 (13thFebruary 2018) To 5 PM, 15thFalgun 2074 (27thFebruary 2018) Admit card can be downloaded during Falgun17-18, 2074 from the website: http://entrance.ioe.edu.np OR www.ioe.edu.np/entrance Entrance Examination will be held at ICTC, IOE, Pulchowk: 19-20 Falgun2074 (March3-4, 2018) Publication of Result:By 25thof Falgun, 2074 (By 9thMarch, 2018) To be eligible for master’s entrance application, the candidate must have passed bachelor degree in relevant subjects with at least second division. Admission Notice for the successful candidates shall be published by the Admission Committee of Constituent Campuses of IOE. The Academic session starts from 16thBaisakh 2075 (29thApril, 2018) lq=lj= OlGhlgol/Ë cWoog ;+:yfgåf/f z}lIfs aif{ @)&$÷)&% df ;+rfng ul/g] :gftsf]Q/ txsf] k|a]z k/LIff ptL0f{ ug{] k/LIffyL{x? g]kfn ;/sf/, lzIff dGqfnosf] 5fqa[lQ ;DaGwL lgodfjnL cg';f/ tf]lsPsf] sfg'gL dfkb08 k'/f u/]df ;f] dGqfnoåf/f @)&$÷)&% df k|bfg ul/g] :gftsf]Q/ txsf pRr lzIffsf 5fqa[lQx?sf nflu ;d]t pDd]bjf/ x'g of]Uo x'g]5g\ . 1 INTRODUCTION 1.1 History of IOE History of engineering education in Nepal can be traced to 1942 AD, when Technical Training School was established.
    [Show full text]
  • QAA Annual Report 2075/76
    HEQAAC 68 Annual Report 2075/076 (2018/019) HIGHER EDUCATION QUALITY ASSURANCE AND ACCREDITATION COUNCIL ANNUAL REPORT 2075/076 (2018/019) UNIVERSITY GRANTS COMMISSION QUALITY ASSURANCE AND ACCREDITATION DIVISION SANOTHIMI, BHAKTAPUR, NEPAL HEQAAC 2075/076 (2018/019) Annual Report 69 ANNUAL REPORT OF HIGHER EDUCATION QUALITY ASSURANCE AND ACCREDITATION COUNCIL, 2075/076 Copyright © : University Grants Commission, Quality Assurance & Accreditation Council, Sanothimi, Bhaktapur, Nepal Edition : December 2019 (Second) Printed Copies : 500 Layout : Digital Print Nepal, 014332600 Printed at : HEQAAC 70 Annual Report 2075/076 (2018/019) FROM THE DESK OF THE CHAIRMAN igher education is the backbone of development and the future of a nation. Its primary aim is to Hproduce qualified, creative and competitive citizens nationally, regionally and globally. To achieve this aim, governments are making their best efforts through introducing various policies, acts, rules and guidelines and by establishing necessary institutions to manage the system. In Nepal, the University Grants Commission (UGC) was established in 2050 BS (1993 AD) as an apex institution to provide grants and coordinate regulate activities related to higher education. Education policies provide road map to the prosperity of the nation and over the last seven decades i.e., since 1950 the country has also implemented at least eight progressive education policies of Nepal and the ‘National Education Policy 2076’ is the latest one. At present, Nepal has 11 operating Universities, six health-science Academies and 1425 higher education institutions (HEIs) under these universities and academies. More than a hundred HEIs are offering academic programs of foreign universities as well. However, the enrolment rate in higher education is quite low (i.e.
    [Show full text]
  • S.N Branch/RO/Department Extension Counter Manager Contact No
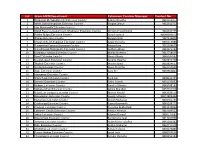
    S.N Branch/RO/Department Extension Counter Manager Contact No 1 Biratnagar Metropolitan City Extension Counter Rubina Shrestha 9841562477 2 Itahari Sub-Metropolitan Extension Counter Sangita Dhakal 9842340732 3 Ilam Municipality Extension Counter 4 lnland Revenue Department, Bhadrapur Extension Counter Nirdesh Prasad Dahal 9842637735 5 Phidim Malpot Extension Counter Narad Tumrok 98049999079 6 Dharan Extension Counter Sanyam Shah 9829316808 7 Dharan Sub- Metropolitan Extension Counter Sawal Shrestha 9804359088 8 Purwanchal Campus Extension Counter Kabita Bista 9852076625 9 Suryabinayak Municipality Extension Counter Sadhana Bhuju 9843073189 10 Bhaktapur- Malpot Extension Counter Malika Shrestha 9813758535 11 Byasi Extension Counter Shova Dhanju 9849347687 12 Neupanegaun Extension Counter Sangita Shyama 9843453750 13 Tikathali Extension Counter Meenu Suwal 9818824657 14 Sirutar Extension Counter Navin Shrestha 9841159590 15 Bode Extension Counter Sony Giri 9849966824 16 Narayantar Extension Counter 17 Shivachowk Extension Counter Rajib Giri 9808323105 18 Danchhi Extension Counter Sushil Subedi 9851195662 19 Mulpani Extension Counter Sumitra Ghimire 9843748181 20 Mahadevsthan Extension Counter Sabina Bhandari 9857017318 21 Nepal Law Campus Extension Counter Monica Poudel 9843936559 22 Baluwakhani Extension Counter Seema Adhikari 98612804444 23 Manamaiju Extension Counter Dinesh Maharjan 9803761195 24 Goldhunga Extension Counter Sujata Gotame Kc 9843296171 25 Phutung Extension Counter Prasanna Budhathoki 9841315699 26 Loktantrik Chowk Extension
    [Show full text]
  • Education Management Information System Report on Higher
    EDUCATION MANAGEMENT INFORMATION REPORT ON HIGHER EDUCATION 2014/15 A.D. SYSTEM (2071/72 B.S.) NEPAL Published in 2016 by: UNIVERSITY GRANTS COMMISION Sanothimi, Bhaktapur, Nepal Post Box : 10796 Telephone : (977-1) 6638548, 6638549, 6638550 Fax : 977-1-6638552 E-mail : [email protected] Website : www.ugcnepal.edu.np Design : Surya Budhathoki (9841190718) [email protected] Print at : Jugal Printers & Traders Anamnagar, Kathmandu Ph. : 01-4246729 Email : [email protected] EDUCATION MANAGEMENT INFORMATION SYSTEM / Report on Higher Education 2014/15 A.D. (2071/72 B.S.) FOREWORD igher Education Management Information System (H-EMIS) remains an important part for strengthening the capacity of higher education system. University Grants Commission has been pursuing the H-EMIS since 2007. HUGC has prepared and adopted a systematic framework for data collection. Managing data and publishing annual report is a regular activity of UGC. It is the eighth year of publication. Credible system of data/information management is one of the crucial activities for higher education reform and development. Since UGC initiated development and implementation of performance based public funding in higher education, it has become imperative to have the data reliable and verifiable. The government of Nepal has recently endorsed and started to implement the national higher education policy that has emphasized on its need for the development of better higher education management system (HEMIS). In addressing the needs, the Higher Education Reform Project (HERP 2015-2020), a national priority project for supporting implementation of the higher education policy aims to build a comprehensive and coordinated HEMIS extending from UGC to the universities and to their respective campuses that is open and accessible to all stakeholders including educational planers, researchers, critiques, faculties, and students.
    [Show full text]
  • Tribhuvan University Institute of Engineering Pulchowk Campus
    TRIBHUVAN UNIVERSITY INSTITUTE OF ENGINEERING PULCHOWK CAMPUS STRATEGIC PLAN (2017-2021) KATHMANDU, 2018 CONTENTS SECTION 1 ................................................................................................................................... 1 INTRODUCTION ........................................................................................................................ 1 1.1 Contexts and Rationale of Strategic Plan .......................................................................................... 1 1.2 Purpose of the Plan ........................................................................................................................... 1 1.3 Process of Preparing the Plan ........................................................................................................... 2 1.4 Participants of Strategic Planning ..................................................................................................... 2 1.5 Stakeholders ...................................................................................................................................... 2 1.6 Components of the Strategic Plan .................................................................................................... 3 1.6.1. Academic Excellence ................................................................................................................. 3 1.6.2 Think‐Tank .................................................................................................................................. 5 1.6.3
    [Show full text]
  • Tribhuvan University
    TRIBHUVAN UNIVERSITY INSTITUTE OF ENGINEERING CHITWAN ENGINEERING CAMPUS,RAMPUR FINAL APPLICANTS FOR CHITWAN ENGINEERING CAMPUS,RAMPUR CENTRE FOR APTITUDE TEST AT PULCHOWK CAMPUS AND PURWANCHAL CAMPUS,Dharan S.NO. Applicants Entrance Roll No. Centre Regular Full Fee Gender 1 Dikshya Aryal 2076-651 Pulchowk 3 4 F 2 Asmita Singh 2076-3193 0 3 0 F 3 Sandip Tapaliya 2076-1495 Pulchowk 3 4 M 4 Tanya Rashi 2076-242 Pulchowk 3 4 F 5 Bishal Neupane 2076-6431 0 0 4 M 6 Prajwal Adhikari 2076-4105 Pulchowk 3 4 M 7 Dipika Poudel 2076-5171 Pulchowk 3 4 F 8 Bandana Dhakal 2076-11008 Pulchowk 3 4 F 9 Aashish Chapagain 2076-642 Pulchowk 3 4 M 10 Ganesh Bahadur Malla 2076-10004 ERC,Dharan 0 4 M 11 Anish Paudel 2076-1448 Pulchowk 0 4 M 12 Amit Poudyal Upadhyay 2076-2579 Pulchowk 3 4 M 13 Sulochana Dhakal 2076-4222 Pulchowk 0 4 F 14 Sonia Gaire 2076-8 Pulchowk 3 4 F 15 Aagya Dhungana 2076-5455 Pulchowk 0 4 F 16 Suchana Sharma 2076-3753 Pulchowk 3 4 F 17 Shikshya Dawadi 2076-7832 ERC,Dharan 3 4 F 18 Ritisha Chalise 2076-191 Pulchowk 3 4 F 19 Priya Sah 2076-893 Pulchowk 0 4 F 20 Krishma Kandel 2076-1590 Pulchowk 0 4 F 21 Dhiraj Kumar Sah 2076-4844 Pulchowk 3 4 M 22 Hitesh Thapa 2076-10434 Pulchowk 3 4 M 23 Sagar Neupane 2076-2223 ERC,Dharan 0 4 M 24 Shankar Kumar Yadav 2076-2741 Pulchowk 3 4 M 25 Arjun Kumar Chaudhary 2076-4575 Pulchowk 3 4 M 26 Manish Dhungana 2076-222 Pulchowk 3 0 M 27 Kiran Rijal 2076-1647 Pulchowk 0 4 M 28 Ayush Deep Neupane 2076-7294 Pulchowk 0 4 M 29 Anjila Timsina 2076-5669 0 3 4 F 30 Cson Shiwakoti 2076-1991 0 3 4 F 31 Anju Nagarkoti
    [Show full text]
  • Devi-P.-Bhattarai.Pdf
    CIVIL DEPARTMENT, PULCHOWK CAMPUS, INSTITUTE OF ENGINEERING Faculty: Civil Engineering/ Water Resources Engineering Name: Debi Prasad Bhattarai Professor Existing Position: E - Mail: [email protected] Phone Office: 5525477 Recent Photo Phone Home: 6638416 Phone Extension: ………………………………… Education PCL in Science (Physical group) Bachelor’s Degree in Civil Engineering Master’s Degree in Water Resources Management PhD ( studying at Department of Civil Engineering, Pulchowk Campus ) Academic Awards/Scholarships a. Winner of Ratna Shield Inter Campus Quiz Contest organized by GAA,Kathmandu b. Selected for scholarship program to take-up studies leading to BE(Civil Engineering) offered by Government of India in 1986. c. Selected for NFP scholarship program to study Masters Program in Water Resources Management in The Netherlands for the year 2003-2005 Research Areas Water Resources Management Research Interests Climate change and Hydropower Development Work Experiences (only mention the academic experiences) Director of Center for Pollution Studies: Institute of Engineering since Nov, 2013 till March 2016. CIVIL DEPARTMENT, PULCHOWK CAMPUS, INSTITUTE OF ENGINEERING Professor: Tribhuvan University, Institute of Engineering since April 2012 till now Associate Professor : Institute of Engineering since Oct, 2005 to 23rd April 2012 Lecturer : Institute of Engineering since Dec, 1990 to Sept 2005 Worked as a faculty of Civil Engineering at Institute of Engineering Pulchowk and Purwanchal Campus from last 25 years Worked as the Head of Civil Engineering Department, Purwanchal Campus Dharan from 16th Dec 1992 -15th April 1998 Assistant Education Officer: (Under Engineering Education Project, IOE) (22/11/1998- 3 /09/1998) Worked as an Assistant Campus Chief at Purwanchal Campus from 12/09/2000 to 11/09, 2002 Worked as a Campus Chief at Purwanchal Campus from 4/07/ 2006- 24/01/ 2007 Theses Supervised: Doctoral Theses Supervised ……………………………………………………………………………………….
    [Show full text]
  • ENGIEERING Web2071-2072.Pdf
    lghfdtL sd{rf/L ;Gtlt 5fqj[lQ )&!÷)&@ df 5gf}6 ePsf ljBfyL{x?sf] ljj/0f ljifoM Ol~hlgol/ª (ENGINEERING) hDdf l;6 ;+VofM !%$ v'nftkm{ M *%+& -blnt %, ckfª\utf ePsf JolQm @ l;6 yk ul/Psf]_ cfj]bg lbg] hDdf pDd]bjf/M @^^ kb÷;]jf÷>]0f cWoog/t lzIf0f ;+:yfsf] gfd, 7]ufgf ;+s]t g+== laifo ljBfyL{sf] gfd sd{rf/Lsf] gfd, y/ sd{rf/Lsf] sfof{no egf{ jif{ lnË l;=g+= btf{ g+= L ;Dks{ g+=/ Od]n cf}ift k|fKtfª 1 68 sf}/a uf}td b]jL k|;fb uf}td lhNnf jg sfof{no, dsjfgk'/, x]6f}+8f jg /Ifs ENGINEERING 2071 Thapathali Campus, Thapathali M 88.86 2 399 gljg cfrfo{ gf/fo0f k|;fb cfrfo{ ,710873 vfg]kfgL tyf ;/;kmfO{ l8lehg l;=l8=O{= ENGINEERING 2071 Kathmandu Engineering College, M 87.67 sfof{no, uf]/vf Kalimati 3 424 ?s'df zdf{ /fh]Gb| k|;fb zdf{ ,156150 l;+rfO ljefu, nlntk'/ l;=l8=O{= ENGINEERING 2071 Central Campus, Pulchowk F 87.58 4 352 >j0f lbk uf}td tLy{ /fh uf}td ,159396 lhNnf :jf:Yo sfof{no, d+un;]g, tYof+s ENGINEERING 2071 Tribhuvan University Institute of M 87.36 c5fd clws[t Engineering Central Campus Pulchowk, Lalitpur 5 14 k|zfGt bfxfn e"k/fh bfxfn ,118796 lhNnf ljsf; ;ldltsf] sfof{no, uf=lj=;=;lrj ENGINEERING 2071 Central Campus, Pulchowk M 86.60 nlntk'/ -zf=c_ Page 1 6 322 ldng e§/fO{ gf/fo0f k|;fb e§/fO{ ,117879 klZrdf~rn l;+rfO ljsf; l8lehg g+ sfof{no ENGINEERING 2071 TU Institute of Engineering M 86.53 ^, ?kGb]xL ;xof]uL Pashchimanchal Campus, Pokhara 7 414 k|zfGt sfsL{ s]bf/ sfsL{ ,140566 >L dWodf~rn If]qLo x'nfs n]vf clws[t ENGINEERING 2071 Central Campus, Pulchowk M 86.48 lgb]{zgfno, aa/dxn § 8 519 k|Hjn e /fO{ dfwj k|;fb e§/fO{ ,154760
    [Show full text]
  • Golden Jubilee Scholarship 2015-16
    LIST OF SUCCESSFUL STUDENTS FOR GOLDEN JUBILEE SCHOLARSHIP SCHEME (GJSS) 2015-16 (Results) Candidates are requested to read the instructions carefully. Students may kindly submit in person one copy of the following alongwith original for verifications on any working day between 9:30 - 12:30 hrs on or before 22 Jan 2016 i.) Marksheet (Original and one Photocopy) ii.) Income Certificate (Original) iii.) School/College Recommendation Letter (specifying government or private; and studying in Bachelor 1st Yr/Sem. - Original) iv.) Certificate of Dalit and Physically challenge applicant (original) S.NO C. Code Course First Name Last Name Gen. Father Studying Institute 1 GJSS2015‐01092 MBBS kushal poudel M shesh narayan paudel Maharajgunj Medical Campus 2 GJSS2015‐01314 MBBS Bimochan dahal M Dik Prasad dahal Maharajgunjjg j Medical Campusp 3 GJSS2015‐01229 MBBS sabina rijal F laxmi prasad rijal Nepalese Army Institute of Health Sciences ‐ College o 4 GJSS2015‐01450 MBBS alisha adhikari F bal bahadur adhikari nepalese army institute of health science 5 GJSS2015‐00781 MBBS shishir koirala M indra prasad koirala Universal college of medical sciences, Ranigaon, Bhaira 6 GJSS2015‐01143 MBBS bibek man shrestha M basanta man shrestha institute of medicine 7 GJSS2015‐00168 MBBS bikash baral M hari prasad baral maharajgunj medical campus 8 GJSS2015‐00139 MBBS sital thapa M jitendra thapa maharjung medical campus (iom) 9 GJSS2015‐00520 MBBS sneha singh F avimanyu lal singh Nepalese Army Institute of Health Sciences 10 GJSS2015‐01114 MBBS prakash gyawali M bhim lal gyawali institute of medicine 11 GJSS2015‐01193 MBBS Pradeep khatiwada M Bhawani prasad khatiwada B.P.
    [Show full text]
  • 1 Curriculum Vitae
    CURRICULUM VITAE Name: Dubi Nanda Dhakal Permanent Address: Kaligandaki Village Assembly-6 [formerly Khadgakot Village Development Committee, Ward No 5], Gulmi, Lumbini Province No.5 Designation: Professor and Head Central Department of Linguistics Tribhuvan University, Kirtipur, Kathmandu, Nepal Advisor, Language Commission, Nepal Webpage: https://cdltu.edu.np/academic/ Email: [email protected]; [email protected] Mobile: 9841575511 Telephone (office): 014330696 QUALIFICATIONS SN Degrees Board/University Year Specialization 1 Doctor of Philosophy Tribhuvan University 2011 Linguistics 2 Master's Degree in Linguistics Tribhuvan Univeristy 2006 First Class First (Gold Medalist) 3 Master's Degree in English Tribhuvan University 1996 English literature 4 Bachelor's Degree (BA) Tribhuvan University 1992 English, Economics 5 Intermediate in Education Tribhuvan University 1988 English, Economics 6 School Leaving Certificate S.L.C. Board, Nepal 1986 SCHOOLS/INSTITUTES ATTENDED 1. Institute on Field Linguistics and Language Documentation, University of California at Santa Barbara, USA, June-July 2007. 2. Putting Fieldwork on Indigenous languages in New Uses (PFLLNU), University of Unicamp, Campinas, Brazil, 21 March to April 6, 2016. [https://sites.google.com /site/pfilnu/] RESEARCH INTERESTS My major research interest lies in language documentation and description, morphology, fieldwork, lexicography, grammatical description of lesser-described languages, language contact, field linguistics etc. LANGUAGES MATERIALS ARCHIVE I have worked on different language documentation projects. The materials related to Documenting the langauges of Manang can be seen at <https://mananglanguages.isg.siue.edu/index.php /home/archive/>. The archive contains the materials of four different langauges spoken in the Manang district, viz. Manang Gurung, Gyalsumdo, Nar-Phu, and Manange. I worked as a researcher in this project.
    [Show full text]