Classes of Languages Generated by the Kleene Star of a Word
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
Deterministic Finite Automata 0 0,1 1
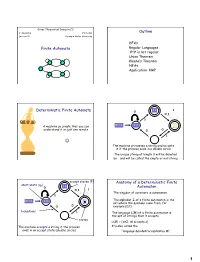
Great Theoretical Ideas in CS V. Adamchik CS 15-251 Outline Lecture 21 Carnegie Mellon University DFAs Finite Automata Regular Languages 0n1n is not regular Union Theorem Kleene’s Theorem NFAs Application: KMP 11 1 Deterministic Finite Automata 0 0,1 1 A machine so simple that you can 0111 111 1 ϵ understand it in just one minute 0 0 1 The machine processes a string and accepts it if the process ends in a double circle The unique string of length 0 will be denoted by ε and will be called the empty or null string accept states (F) Anatomy of a Deterministic Finite start state (q0) 11 0 Automaton 0,1 1 The singular of automata is automaton. 1 The alphabet Σ of a finite automaton is the 0111 111 1 ϵ set where the symbols come from, for 0 0 example {0,1} transitions 1 The language L(M) of a finite automaton is the set of strings that it accepts states L(M) = {x∈Σ: M accepts x} The machine accepts a string if the process It’s also called the ends in an accept state (double circle) “language decided/accepted by M”. 1 The Language L(M) of Machine M The Language L(M) of Machine M 0 0 0 0,1 1 q 0 q1 q0 1 1 What language does this DFA decide/accept? L(M) = All strings of 0s and 1s The language of a finite automaton is the set of strings that it accepts L(M) = { w | w has an even number of 1s} M = (Q, Σ, , q0, F) Q = {q0, q1, q2, q3} Formal definition of DFAs where Σ = {0,1} A finite automaton is a 5-tuple M = (Q, Σ, , q0, F) q0 Q is start state Q is the finite set of states F = {q1, q2} Q accept states : Q Σ → Q transition function Σ is the alphabet : Q Σ → Q is the transition function q 1 0 1 0 1 0,1 q0 Q is the start state q0 q0 q1 1 q q1 q2 q2 F Q is the set of accept states 0 M q2 0 0 q2 q3 q2 q q q 1 3 0 2 L(M) = the language of machine M q3 = set of all strings machine M accepts EXAMPLE Determine the language An automaton that accepts all recognized by and only those strings that contain 001 1 0,1 0,1 0 1 0 0 0 1 {0} {00} {001} 1 L(M)={1,11,111, …} 2 Membership problem Determine the language decided by Determine whether some word belongs to the language. -

1 Alphabets and Languages
1 Alphabets and Languages Look at handout 1 (inference rules for sets) and use the rules on some exam- ples like fag ⊆ ffagg fag 2 fa; bg, fag 2 ffagg, fag ⊆ ffagg, fag ⊆ fa; bg, a ⊆ ffagg, a 2 fa; bg, a 2 ffagg, a ⊆ fa; bg Example: To show fag ⊆ fa; bg, use inference rule L1 (first one on the left). This asks us to show a 2 fa; bg. To show this, use rule L5, which succeeds. To show fag 2 fa; bg, which rule applies? • The only one is rule L4. So now we have to either show fag = a or fag = b. Neither one works. • To show fag = a we have to show fag ⊆ a and a ⊆ fag by rule L8. The only rules that might work to show a ⊆ fag are L1, L2, and L3 but none of them match, so we fail. • There is another rule for this at the very end, but it also fails. • To show fag = b, we try the rules in a similar way, but they also fail. Therefore we cannot show that fag 2 fa; bg. This suggests that the state- ment fag 2 fa; bg is false. Suppose we have two set expressions only involving brackets, commas, the empty set, and variables, like fa; fb; cgg and fa; fc; bgg. Then there is an easy way to test if they are equal. If they can be made the same by • permuting elements of a set, and • deleting duplicate items of a set then they are equal, otherwise they are not equal. -

Context Free Languages II Announcement Announcement
Announcement • About homework #4 Context Free Languages II – The FA corresponding to the RE given in class may indeed already be minimal. – Non-regular language proofs CFLs and Regular Languages • Use Pumping Lemma • Homework session after lecture Announcement Before we begin • Note about homework #2 • Questions from last time? – For a deterministic FA, there must be a transition for every character from every state. Languages CFLs and Regular Languages • Recall. • Venn diagram of languages – What is a language? Is there – What is a class of languages? something Regular Languages out here? CFLs Finite Languages 1 Context Free Languages Context Free Grammars • Context Free Languages(CFL) is the next • Let’s formalize this a bit: class of languages outside of Regular – A context free grammar (CFG) is a 4-tuple: (V, Languages: Σ, S, P) where – Means for defining: Context Free Grammar • V is a set of variables Σ – Machine for accepting: Pushdown Automata • is a set of terminals • V and Σ are disjoint (I.e. V ∩Σ= ∅) •S ∈V, is your start symbol Context Free Grammars Context Free Grammars • Let’s formalize this a bit: • Let’s formalize this a bit: – Production rules – Production rules →β •Of the form A where • We say that the grammar is context-free since this ∈ –A V substitution can take place regardless of where A is. – β∈(V ∪∑)* string with symbols from V and ∑ α⇒* γ γ α • We say that γ can be derived from α in one step: • We write if can be derived from in zero –A →βis a rule or more steps. -

Kleene Algebra with Tests and Coq Tools for While Programs Damien Pous
Kleene Algebra with Tests and Coq Tools for While Programs Damien Pous To cite this version: Damien Pous. Kleene Algebra with Tests and Coq Tools for While Programs. Interactive Theorem Proving 2013, Jul 2013, Rennes, France. pp.180-196, 10.1007/978-3-642-39634-2_15. hal-00785969 HAL Id: hal-00785969 https://hal.archives-ouvertes.fr/hal-00785969 Submitted on 7 Feb 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Kleene Algebra with Tests and Coq Tools for While Programs Damien Pous CNRS { LIP, ENS Lyon, UMR 5668 Abstract. We present a Coq library about Kleene algebra with tests, including a proof of their completeness over the appropriate notion of languages, a decision procedure for their equational theory, and tools for exploiting hypotheses of a certain kind in such a theory. Kleene algebra with tests make it possible to represent if-then-else state- ments and while loops in most imperative programming languages. They were actually introduced by Kozen as an alternative to propositional Hoare logic. We show how to exploit the corresponding Coq tools in the context of program verification by proving equivalences of while programs, correct- ness of some standard compiler optimisations, Hoare rules for partial cor- rectness, and a particularly challenging equivalence of flowchart schemes. -

Context-Free Languages ∗
Chapter 17: Context-Free Languages ¤ Peter Cappello Department of Computer Science University of California, Santa Barbara Santa Barbara, CA 93106 [email protected] ² Please read the corresponding chapter before attending this lecture. ² These notes are not intended to be complete. They are supplemented with figures, and material that arises during the lecture period in response to questions. ¤Based on Theory of Computing, 2nd Ed., D. Cohen, John Wiley & Sons, Inc. 1 Closure Properties Theorem: CFLs are closed under union If L1 and L2 are CFLs, then L1 [ L2 is a CFL. Proof 1. Let L1 and L2 be generated by the CFG, G1 = (V1;T1;P1;S1) and G2 = (V2;T2;P2;S2), respectively. 2. Without loss of generality, subscript each nonterminal of G1 with a 1, and each nonterminal of G2 with a 2 (so that V1 \ V2 = ;). 3. Define the CFG, G, that generates L1 [ L2 as follows: G = (V1 [ V2 [ fSg;T1 [ T2;P1 [ P2 [ fS ! S1 j S2g;S). 2 4. A derivation starts with either S ) S1 or S ) S2. 5. Subsequent steps use productions entirely from G1 or entirely from G2. 6. Each word generated thus is either a word in L1 or a word in L2. 3 Example ² Let L1 be PALINDROME, defined by: S ! aSa j bSb j a j b j Λ n n ² Let L2 be fa b jn ¸ 0g defined by: S ! aSb j Λ ² Then the union language is defined by: S ! S1 j S2 S1 ! aS1a j bS1b j a j b j Λ S2 ! aS2b j Λ 4 Theorem: CFLs are closed under concatenation If L1 and L2 are CFLs, then L1L2 is a CFL. -

Formal Languages We’Ll Use the English Language As a Running Example
Formal Languages We’ll use the English language as a running example. Definitions. Examples. A string is a finite set of symbols, where • each symbol belongs to an alphabet de- noted by Σ. The set of all strings that can be constructed • from an alphabet Σ is Σ ∗. If x, y are two strings of lengths x and y , • then: | | | | – xy or x y is the concatenation of x and y, so the◦ length, xy = x + y | | | | | | – (x)R is the reversal of x – the kth-power of x is k ! if k =0 x = k 1 x − x, if k>0 ! ◦ – equal, substring, prefix, suffix are de- fined in the expected ways. – Note that the language is not the same language as !. ∅ 73 Operations on Languages Suppose that LE is the English language and that LF is the French language over an alphabet Σ. Complementation: L = Σ L • ∗ − LE is the set of all words that do NOT belong in the english dictionary . Union: L1 L2 = x : x L1 or x L2 • ∪ { ∈ ∈ } L L is the set of all english and french words. E ∪ F Intersection: L1 L2 = x : x L1 and x L2 • ∩ { ∈ ∈ } LE LF is the set of all words that belong to both english and∩ french...eg., journal Concatenation: L1 L2 is the set of all strings xy such • ◦ that x L1 and y L2 ∈ ∈ Q: What is an example of a string in L L ? E ◦ F goodnuit Q: What if L or L is ? What is L L ? E F ∅ E ◦ F ∅ 74 Kleene star: L∗. -

Finite-State Automata and Algorithms
Finite-State Automata and Algorithms Bernd Kiefer, [email protected] Many thanks to Anette Frank for the slides MSc. Computational Linguistics Course, SS 2009 Overview . Finite-state automata (FSA) – What for? – Recap: Chomsky hierarchy of grammars and languages – FSA, regular languages and regular expressions – Appropriate problem classes and applications . Finite-state automata and algorithms – Regular expressions and FSA – Deterministic (DFSA) vs. non-deterministic (NFSA) finite-state automata – Determinization: from NFSA to DFSA – Minimization of DFSA . Extensions: finite-state transducers and FST operations Finite-state automata: What for? Chomsky Hierarchy of Hierarchy of Grammars and Languages Automata . Regular languages . Regular PS grammar (Type-3) Finite-state automata . Context-free languages . Context-free PS grammar (Type-2) Push-down automata . Context-sensitive languages . Tree adjoining grammars (Type-1) Linear bounded automata . Type-0 languages . General PS grammars Turing machine computationally more complex less efficient Finite-state automata model regular languages Regular describe/specify expressions describe/specify Finite describe/specify Regular automata recognize languages executable! Finite-state MACHINE Finite-state automata model regular languages Regular describe/specify expressions describe/specify Regular Finite describe/specify Regular grammars automata recognize/generate languages executable! executable! • properties of regular languages • appropriate problem classes Finite-state • algorithms for FSA MACHINE Languages, formal languages and grammars . Alphabet Σ : finite set of symbols Σ . String : sequence x1 ... xn of symbols xi from the alphabet – Special case: empty string ε . Language over Σ : the set of strings that can be generated from Σ – Sigma star Σ* : set of all possible strings over the alphabet Σ Σ = {a, b} Σ* = {ε, a, b, aa, ab, ba, bb, aaa, aab, ...} – Sigma plus Σ+ : Σ+ = Σ* -{ε} Strings – Special languages: ∅ = {} (empty language) ≠ {ε} (language of empty string) . -

Transducers and Rational Relations
Transducers and Rational Relations A. Anil & K. Sutner Carnegie Mellon University Spring 2018 1 Rational Relations Properties of Rat Wisdom 3 The author (along with many other people) has come recently to the conclusion that the func- tions computed by the various machines are more important–or at least more basic–than the sets accepted by these devices. D. Scott, “Some Definitional Suggestions for Automata Theory,” 1967 Quoi? 4 Acceptor A machine that checks membership in some language L Σ? ⊆ (a machine that solves a decision problem). Transducer A machine that computes a function f :Σ? Σ? → or a relation R Σ? Σ? ⊆ × We will focus on relations (functions are just a special kind). Example: Lexicographic Order 5 How do we check whether a word u is lexicographically less than v? Find the longest common prefix x (so u = xu0 and v = xv0). Handle the case where u0 = ε or v0 = ε. Otherwise, compare u10 and v10 . Insight: We scan the input once, left-to-right; our decisions require no extra memory. This looks just like a DFA, except there are two inputs. Two-Tape DFA 6 Y a b c a a b ℳ b b a a b a c a N Details? 7 We will not give a careful definition of how a k-tape DFA works and appeal to your intuition instead. The main idea is to use transitions of the form x/y p q −→ where the labels are in the following form: a/b and a/ε and ε/b. You can think of this as the transducer checking for an a on the first tape, and a b on the second tape. -

CMPSCI 250 Lecture
CMPSCI 250: Introduction to Computation Lecture #29: Proving Regular Language Identities David Mix Barrington 6 April 2012 Proving Regular Language Identities • Regular Language Identities • The Semiring Axioms Again • Identities Involving Union and Concatenation • Proving the Distributive Law • The Inductive Definition of Kleene Star • Identities Involving Kleene Star • (ST)*, S*T*, and (S + T)* Regular Language Identities • In this lecture and the next we’ll use our new formal definition of the regular languages to prove things about them. In particular, in this lecture we’ll prove a number of regular language identities, which are statements about languages where the types of the free variables are “regular expression” and which are true for all possible values of those free variables. • For example, if we view the union operator + as “addition” and the concatenation operator ⋅ as “multiplication”, then the rule S(T + U) = ST + SU is a statement about languages and (as we’ll prove today) is a regular language identity. In fact it’s a language identity as regularity doesn’t matter. • We can use the inductive definition of regular expressions to prove statements about the whole family of them -- this will be the subject of the next lecture. The Semiring Axioms Again • The set of natural numbers, with the ordinary operations + and ×, forms an algebraic structure called a semiring. Earlier we proved the semiring axioms for the naturals from the Peano axioms and our inductive definitions of + and ×. It turns out that the languages form a semiring under union and concatenation, and the regular languages are a subsemiring because they are closed under + and ⋅: if R and S are regular, so are R + S and R⋅S. -

Cfls and Regular Languages Homework Schedule Mangling
Homework • Assignment #6 (Due 10/26) – From textbook CFLs and Regular Languages • Exercise 6.2.1 b,c / 6.2.2 b (use JFLAP) • Exercise 6.3.2 (by empty stack or final state) • Exercise 6.3.4 • Exercise 7.1.5 – Other problems • Define CFGs that generate the following langauges: –{aibjck | j = i + k } –{aibjck | j = i or j = k } Schedule mangling Before we begin • The schedule on the Web has been adjusted • Questions from last time? – This week: Chapter 7 • Finish Context Free Languages – Next week • Start Turing Machines Languages Context Free Languages • Future Exam Question • Context Free Languages(CFL) is the next – What is a language? class of languages outside of Regular – What is a class of languages? Languages: – Means for defining: Context Free Grammar – Machine for accepting: Pushdown Automata 1 Context Free Grammars Context Free Grammars • Let’s formalize this a bit: • Let’s formalize this a bit: – A context free grammar (CFG) is a 4-tuple: (V, – Production rules T, S, P) where •Of the form A →βwhere –A ∈V • V is a set of variables – β∈(V ∪∑)* string with symbols from V and ∑ • T is a set of terminals • We say that γ can be derived from α in one step: • V and Σ are disjoint (I.e. V ∩Σ= ∅) –A →βis a rule – α = α A α •S ∈V, is your start symbol 1 2 – γ = α1 βα2 – α⇒γ Now our picture looks like CFLs and Regular Languages Context Free Languages • We showed last time that every RL is also a CFL – Since a NFA can simply be described as a PDA that Deterministic Context Free Languages doesn’t use the stack. -

Schützenberger's Aperiodic Monoid Characterization of Star-Free
Sch¨utzenberger's Aperiodic Monoid Char- acterization of Star-Free Languages Sch¨utzenberger's Aperiodic Monoid Characterization of Star-Free Languages Nov 2019 Sch¨utzenberger's Prelude Aperiodic Monoid Char- acterization of Star-Free Languages • A star-free language is one that can be described by a regular expression constructed from the letters of the alphabet, the empty set symbol, all boolean operators, but no Kleene star. • They can also be characterized logically as languages definable in FO[<]. • and as languages definable in linear temporal logic • Marcel-Paul Sch¨utzenberger characterized star-free languages as those with aperiodic syntactic monoids Sch¨utzenberger's Monoids Aperiodic Monoid Char- acterization of Star-Free Languages Definition : A `monoid' is a set M 6= ; equipped with a binary operation · : M × M ! M such that • a· (b · c) = (a · b) · c for all a; b; c 2 M •9 1 2 M such that a · 1 = a = 1 · a for all a 2 M Here, 1 is called the `identity' element of M. Also, the identity must be unique. We denote the monoid and it's operation along with it's identity by a triplet (M; ·; 1) Sch¨utzenberger's Monoids : Examples Aperiodic Monoid Char- acterization of Star-Free Languages • (Z; +; 0) i.e the set of integers with integer addition, and 0 as the additive identity. • (N; ·; 1) i.e the set of positive integers with integer multiplication, and 1 as the multiplicative identity. ¯ • For any n 2 N,(Zn; +; 0) is a finite monoid, where Zn is the set of residue classes of integers modulo n, + is addition integers modulo n, and 0¯ is the residue class of zero. -

On Minimizing Regular Expressions Without Kleene Star
Electronic Colloquium on Computational Complexity, Report No. 79 (2020) On Minimizing Regular Expressions Without Kleene Star Hermann Gruber1, Markus Holzer2, and Simon Wolfsteiner3 1 Knowledgepark GmbH, Leonrodstr. 68, 80636 M¨unchen, Germany [email protected] 2 Institut f¨urInformatik, Universit¨atGiessen, Arndtstr. 2, 35392 Giessen, Germany [email protected] 3 Institut f¨urDiskrete Mathematik und Geometrie, TU Wien, Wiedner Hauptstr. 8{10, 1040 Wien, Austria [email protected] Abstract. Finite languages lie at the heart of literally every regular expression. Therefore, we investigate the approximation complexity of minimizing regular expressions without Kleene star, or, equivalently, regular expressions describing finite languages. On the side of approx- imation hardness, given such an expression of size s, we prove that it is impossible to approximate the minimum size required by an equiva- s lent regular expression within a factor of O (log s)2+δ if the running time is bounded by a quasipolynomial function depending on δ, for ev- ery δ > 0, unless the exponential time hypothesis (ETH) fails. For ap- proximation ratio O(s1−δ), we prove an exponential time lower bound depending on δ, assuming ETH. The lower bounds apply for alphabets of constant size. On the algorithmic side, we show that the problem can s log log s be approximated in polynomial time within O( log s ), with s being the size of the given regular expression. For constant alphabet size, the s bound improves to O( log s ). Finally, we devise a familiy of superpoly- nomial approximation algorithms that attain the performance ratios of the lower bounds, while their running times are only slightly above those excluded by the ETH.