DOCSLIB.ORG

Matrices Matrix Addition, Multiplication, Inverse

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Matrices Matrix Addition, Multiplication, Inverse ICS 141: Discrete Mathematics I (Fall 2014) 2.6 Matrices A matrix is a rectangular array of numbers. A matrix with m rows and n columns is called an m × n matrix. 2 1 2 3 3 6 4 5 6 7 6 7 is a 4 × 3 matrix. 4 7 8 9 5 10 11 12 We specify an element of the matrix with mi;j where the element is at row i and column j. For example, m2;3 = 6. Matrix Equality Matrices are equal if and only if they have the same number of rows, the same number of columns, and the same elements at every index. Matrix Addition We can only perform matrix addition if the matrices have the same dimensions. To express the addition of two matrices, A and B, we write A + B = [ai;j + bi;j]. Then simply add the values at corresponding indices. 21 2 33 29 8 73 2(1 + 9) (2 + 8) (3 + 7)3 210 10 103 44 5 65 + 46 5 45 = 4(4 + 6) (5 + 5) (6 + 4)5 = 410 10 105 7 8 9 3 2 1 (7 + 3) (8 + 2) (9 + 1) 10 10 10 Matrix Multiplication If A and B are matrices, we can write AB to denote their multiplication. Matrix multiplication is not commutative (AB 6= BA). We can only multiply matrices if and only if the first matrix has the same number of columns as the number of rows in the second matrix. AB = C A is an i × k matrix B is an k × j matrix The result C is an i × j matrix Ci;j = (ai;1b1;j) + (ai;2b2;j) + (ai;2b2;j) + ::: + (ai;kbk;j) 1 2 5 6 (1 · 5 + 2 · 7) (1 · 6 + 2 · 8) 19 22 = = 3 4 7 8 (3 · 5 + 4 · 7) (3 · 6 + 4 · 8) 43 50 1 ICS 141: Discrete Mathematics I (Fall 2014) Identity Matrix The identity matrix is a n × n square matrix where the main diagonal consist of all ones and zeros elsewhere. 21 0 ::: 03 60 1 ::: 07 6 7 In = 6. .. .7 4. .5 0 0 ::: 1 Inverse Matrix For a square matrix A, the inverse written as A−1. If A is multiplied by A−1, then the result is the −1 −1 identity matrix. AA = A A = In. Note that not all square matrices have an inverse. Power of Matrices Square matrices can be multiplied by themselves repeatedly because they have the same number of rows and columns. An n × n matrix A raised to the positive integer k is defined as Ak = AAA : : : A A0 = I Transpose of Matrices The Transpose of A, denoted by At, is obtained by turning all the rows into columns and vice versa. Zero-One Matrices Zero-one matrices are matrices that only contain 0 or 1. Join: A _ B = [aij _ bij] Meet: A ^ B = [aij ^ bij] Boolean Product: Denoted by A B, where cij = (ai1 ^ b1j) _ (ai2 ^ b2j) _ ::: _ (aik ^ bkj) 2.6 pg 184 # 3 Find AB if 2 1 0 4 a) A = ;B = 3 2 1 3 2 1 0 4 (2 · 0 + 1 · 1) (2 · 4 + 1 · 3) 1 11 = = 3 2 1 3 (3 · 0 + 2 · 1) (3 · 4 + 2 · 3) 2 18 2 ICS 141: Discrete Mathematics I (Fall 2014) 21 −13 3 2 −1 b) A = 0 1 ;B = 4 5 1 0 3 2 3 21 −13 2(1 · 3 + (−1) · 1) (1 · 2 + (−1) · 0) (1 · (−1) + (−1) · 3)3 3 2 −1 0 1 = (0 · 3 + 1 · 1) (0 · 2 + 1 · 0) (0 · (−1) + 1 · 3) 4 5 1 0 3 4 5 2 3 (2 · 3 + 3 · 1) (2 · 2 + 3 · 0) (2 · (−1) + 3 · 3) 22 2 −43 = 41 0 3 5 9 4 7 2.6 pg 185 # 15 Let 1 1 A = 0 1 Find a formula for An, whenever n is a positive integer. 1 1 1 1 1 2 A2 = AA = = 0 1 0 1 0 1 1 1 1 2 1 3 A3 = AA2 = = 0 1 0 1 0 1 1 1 1 3 1 4 A4 = AA3 = = 0 1 0 1 0 1 . 1 1 1 n − 1 1 n An = AAn−1 = = 0 1 0 1 0 1 2.6 pg 185 # 19 Let A be the 2 × 2 matrix a b A = c d Show that if ad − bc 6= 0, then 2 d −b 3 −1 6ad − bc ad − bc7 A = 4 −c a 5 ad − bc ad − bc 2 d −b 3 2ad − bc −ab + ba3 a b 1 0 AA−1 = 6ad − bc ad − bc7 = 6ad − bc ad − bc 7 = c d 4 −c a 5 4cd − cd −bc + ad5 0 1 ad − bc ad − bc ad − bc ad − bc 3 ICS 141: Discrete Mathematics I (Fall 2014) 2 d −b 3 2 ad − bc db − bd 3 a b 1 0 A−1A = 6ad − bc ad − bc7 = 6 ad − bc ad − bc 7 = 4 −c a 5 c d 4−ca + ac −bc + ad5 0 1 ad − bc ad − bc ad − bc ad − bc Extra Problem Let 21 1 1 33 A = 42 0 4 65 1 1 3 7 What is At? 21 2 13 t 61 0 17 A = 6 7 41 4 35 3 6 7 2.6 pg 185 # 27 21 0 13 20 1 13 Let A = 41 1 05 and B = 41 0 15 Find 0 0 1 1 0 1 a) A _ B 21 0 13 20 1 13 21 1 13 41 1 05 _ 41 0 15 = 41 1 15 0 0 1 1 0 1 1 0 1 b) A ^ B 21 0 13 20 1 13 20 0 13 41 1 05 ^ 41 0 15 = 41 0 05 0 0 1 1 0 1 0 0 1 c) A B 21 0 13 20 1 13 41 1 05 41 0 15 0 0 1 1 0 1 2(1 ^ 0) _ (0 ^ 1) _ (1 ^ 1) (1 ^ 1) _ (0 ^ 0) _ (1 ^ 0) (1 ^ 1) _ (0 ^ 1) _ (1 ^ 1)3 = 4(1 ^ 0) _ (1 ^ 1) _ (0 ^ 1) (1 ^ 1) _ (1 ^ 0) _ (0 ^ 0) (1 ^ 1) _ (1 ^ 1) _ (0 ^ 1)5 (0 ^ 0) _ (0 ^ 1) _ (1 ^ 1) (0 ^ 1) _ (0 ^ 0) _ (1 ^ 0) (0 ^ 1) _ (0 ^ 1) _ (1 ^ 1) 21 1 13 = 41 1 15 1 0 1 4.
Load more

Recommended publications
  • Introduction to Linear Bialgebra
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of New Mexico University of New Mexico UNM Digital Repository Mathematics and Statistics Faculty and Staff Publications Academic Department Resources 2005 INTRODUCTION TO LINEAR BIALGEBRA Florentin Smarandache University of New Mexico, [email protected] W.B. Vasantha Kandasamy K. Ilanthenral Follow this and additional works at: https://digitalrepository.unm.edu/math_fsp Part of the Algebra Commons, Analysis Commons, Discrete Mathematics and Combinatorics Commons, and the Other Mathematics Commons Recommended Citation Smarandache, Florentin; W.B. Vasantha Kandasamy; and K. Ilanthenral. "INTRODUCTION TO LINEAR BIALGEBRA." (2005). https://digitalrepository.unm.edu/math_fsp/232 This Book is brought to you for free and open access by the Academic Department Resources at UNM Digital Repository. It has been accepted for inclusion in Mathematics and Statistics Faculty and Staff Publications by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected], [email protected], [email protected]. INTRODUCTION TO LINEAR BIALGEBRA W. B. Vasantha Kandasamy Department of Mathematics Indian Institute of Technology, Madras Chennai – 600036, India e-mail: [email protected] web: http://mat.iitm.ac.in/~wbv Florentin Smarandache Department of Mathematics University of New Mexico Gallup, NM 87301, USA e-mail: [email protected] K. Ilanthenral Editor, Maths Tiger, Quarterly Journal Flat No.11, Mayura Park, 16, Kazhikundram Main Road, Tharamani, Chennai – 600 113, India e-mail: [email protected] HEXIS Phoenix, Arizona 2005 1 This book can be ordered in a paper bound reprint from: Books on Demand ProQuest Information & Learning (University of Microfilm International) 300 N.
    [Show full text]
  • Lesson 2: the Multiplication of Polynomials
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M1 ALGEBRA II Lesson 2: The Multiplication of Polynomials Student Outcomes . Students develop the distributive property for application to polynomial multiplication. Students connect multiplication of polynomials with multiplication of multi-digit integers. Lesson Notes This lesson begins to address standards A-SSE.A.2 and A-APR.C.4 directly and provides opportunities for students to practice MP.7 and MP.8. The work is scaffolded to allow students to discern patterns in repeated calculations, leading to some general polynomial identities that are explored further in the remaining lessons of this module. As in the last lesson, if students struggle with this lesson, they may need to review concepts covered in previous grades, such as: The connection between area properties and the distributive property: Grade 7, Module 6, Lesson 21. Introduction to the table method of multiplying polynomials: Algebra I, Module 1, Lesson 9. Multiplying polynomials (in the context of quadratics): Algebra I, Module 4, Lessons 1 and 2. Since division is the inverse operation of multiplication, it is important to make sure that your students understand how to multiply polynomials before moving on to division of polynomials in Lesson 3 of this module. In Lesson 3, division is explored using the reverse tabular method, so it is important for students to work through the table diagrams in this lesson to prepare them for the upcoming work. There continues to be a sharp distinction in this curriculum between justification and proof, such as justifying the identity (푎 + 푏)2 = 푎2 + 2푎푏 + 푏 using area properties and proving the identity using the distributive property.
    [Show full text]
  • 21. Orthonormal Bases
    21. Orthonormal Bases The canonical/standard basis 011 001 001 B C B C B C B0C B1C B0C e1 = B.C ; e2 = B.C ; : : : ; en = B.C B.C B.C B.C @.A @.A @.A 0 0 1 has many useful properties. • Each of the standard basis vectors has unit length: q p T jjeijj = ei ei = ei ei = 1: • The standard basis vectors are orthogonal (in other words, at right angles or perpendicular). T ei ej = ei ej = 0 when i 6= j This is summarized by ( 1 i = j eT e = δ = ; i j ij 0 i 6= j where δij is the Kronecker delta. Notice that the Kronecker delta gives the entries of the identity matrix. Given column vectors v and w, we have seen that the dot product v w is the same as the matrix multiplication vT w. This is the inner product on n T R . We can also form the outer product vw , which gives a square matrix. 1 The outer product on the standard basis vectors is interesting. Set T Π1 = e1e1 011 B C B0C = B.C 1 0 ::: 0 B.C @.A 0 01 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 0 . T Πn = enen 001 B C B0C = B.C 0 0 ::: 1 B.C @.A 1 00 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 1 In short, Πi is the diagonal square matrix with a 1 in the ith diagonal position and zeros everywhere else.
    [Show full text]
  • Multivector Differentiation and Linear Algebra 0.5Cm 17Th Santaló
    Multivector differentiation and Linear Algebra 17th Santalo´ Summer School 2016, Santander Joan Lasenby Signal Processing Group, Engineering Department, Cambridge, UK and Trinity College Cambridge [email protected], www-sigproc.eng.cam.ac.uk/ s jl 23 August 2016 1 / 78 Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... Summary Overview The Multivector Derivative. 2 / 78 Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... Summary Overview The Multivector Derivative. Examples of differentiation wrt multivectors. 3 / 78 Functional Differentiation: very briefly... Summary Overview The Multivector Derivative. Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. 4 / 78 Summary Overview The Multivector Derivative. Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... 5 / 78 Overview The Multivector Derivative. Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... Summary 6 / 78 We now want to generalise this idea to enable us to find the derivative of F(X), in the A ‘direction’ – where X is a general mixed grade multivector (so F(X) is a general multivector valued function of X). Let us use ∗ to denote taking the scalar part, ie P ∗ Q ≡ hPQi. Then, provided A has same grades as X, it makes sense to define: F(X + tA) − F(X) A ∗ ¶XF(X) = lim t!0 t The Multivector Derivative Recall our definition of the directional derivative in the a direction F(x + ea) − F(x) a·r F(x) = lim e!0 e 7 / 78 Let us use ∗ to denote taking the scalar part, ie P ∗ Q ≡ hPQi.
    [Show full text]
  • Algebra of Linear Transformations and Matrices Math 130 Linear Algebra
    Then the two compositions are 0 −1 1 0 0 1 BA = = 1 0 0 −1 1 0 Algebra of linear transformations and 1 0 0 −1 0 −1 AB = = matrices 0 −1 1 0 −1 0 Math 130 Linear Algebra D Joyce, Fall 2013 The products aren't the same. You can perform these on physical objects. Take We've looked at the operations of addition and a book. First rotate it 90◦ then flip it over. Start scalar multiplication on linear transformations and again but flip first then rotate 90◦. The book ends used them to define addition and scalar multipli- up in different orientations. cation on matrices. For a given basis β on V and another basis γ on W , we have an isomorphism Matrix multiplication is associative. Al- γ ' φβ : Hom(V; W ) ! Mm×n of vector spaces which though it's not commutative, it is associative. assigns to a linear transformation T : V ! W its That's because it corresponds to composition of γ standard matrix [T ]β. functions, and that's associative. Given any three We also have matrix multiplication which corre- functions f, g, and h, we'll show (f ◦ g) ◦ h = sponds to composition of linear transformations. If f ◦ (g ◦ h) by showing the two sides have the same A is the standard matrix for a transformation S, values for all x. and B is the standard matrix for a transformation T , then we defined multiplication of matrices so ((f ◦ g) ◦ h)(x) = (f ◦ g)(h(x)) = f(g(h(x))) that the product AB is be the standard matrix for S ◦ T .
    [Show full text]
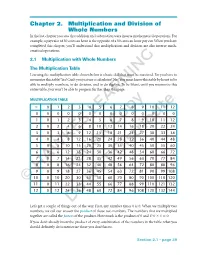
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • The Notion Of" Unimaginable Numbers" in Computational Number Theory
    Beyond Knuth’s notation for “Unimaginable Numbers” within computational number theory Antonino Leonardis1 - Gianfranco d’Atri2 - Fabio Caldarola3 1 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] 2 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy 3 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] Abstract Literature considers under the name unimaginable numbers any positive in- teger going beyond any physical application, with this being more of a vague description of what we are talking about rather than an actual mathemati- cal definition (it is indeed used in many sources without a proper definition). This simply means that research in this topic must always consider shortened representations, usually involving recursion, to even being able to describe such numbers. One of the most known methodologies to conceive such numbers is using hyper-operations, that is a sequence of binary functions defined recursively starting from the usual chain: addition - multiplication - exponentiation. arXiv:1901.05372v2 [cs.LO] 12 Mar 2019 The most important notations to represent such hyper-operations have been considered by Knuth, Goodstein, Ackermann and Conway as described in this work’s introduction. Within this work we will give an axiomatic setup for this topic, and then try to find on one hand other ways to represent unimaginable numbers, as well as on the other hand applications to computer science, where the algorith- mic nature of representations and the increased computation capabilities of 1 computers give the perfect field to develop further the topic, exploring some possibilities to effectively operate with such big numbers.
    [Show full text]
  • Multiplication Fact Strategies Assessment Directions and Analysis
    Multiplication Fact Strategies Wichita Public Schools Curriculum and Instructional Design Mathematics Revised 2014 KCCRS version Table of Contents Introduction Page Research Connections (Strategies) 3 Making Meaning for Operations 7 Assessment 9 Tools 13 Doubles 23 Fives 31 Zeroes and Ones 35 Strategy Focus Review 41 Tens 45 Nines 48 Squared Numbers 54 Strategy Focus Review 59 Double and Double Again 64 Double and One More Set 69 Half and Then Double 74 Strategy Focus Review 80 Related Equations (fact families) 82 Practice and Review 92 Wichita Public Schools 2014 2 Research Connections Where Do Fact Strategies Fit In? Adapted from Randall Charles Fact strategies are considered a crucial second phase in a three-phase program for teaching students basic math facts. The first phase is concept learning. Here, the goal is for students to understand the meanings of multiplication and division. In this phase, students focus on actions (i.e. “groups of”, “equal parts”, “building arrays”) that relate to multiplication and division concepts. An important instructional bridge that is often neglected between concept learning and memorization is the second phase, fact strategies. There are two goals in this phase. First, students need to recognize there are clusters of multiplication and division facts that relate in certain ways. Second, students need to understand those relationships. These lessons are designed to assist with the second phase of this process. If you have students that are not ready, you will need to address the first phase of concept learning. The third phase is memorization of the basic facts. Here the goal is for students to master products and quotients so they can recall them efficiently and accurately, and retain them over time.
    [Show full text]
  • The Classical Matrix Groups 1 Groups
    The Classical Matrix Groups CDs 270, Spring 2010/2011 The notes provide a brief review of matrix groups. The primary goal is to motivate the lan- guage and symbols used to represent rotations (SO(2) and SO(3)) and spatial displacements (SE(2) and SE(3)). 1 Groups A group, G, is a mathematical structure with the following characteristics and properties: i. the group consists of a set of elements {gj} which can be indexed. The indices j may form a finite, countably infinite, or continous (uncountably infinite) set. ii. An associative binary group operation, denoted by 0 ∗0 , termed the group product. The product of two group elements is also a group element: ∀ gi, gj ∈ G gi ∗ gj = gk, where gk ∈ G. iii. A unique group identify element, e, with the property that: e ∗ gj = gj for all gj ∈ G. −1 iv. For every gj ∈ G, there must exist an inverse element, gj , such that −1 gj ∗ gj = e. Simple examples of groups include the integers, Z, with addition as the group operation, and the real numbers mod zero, R − {0}, with multiplication as the group operation. 1.1 The General Linear Group, GL(N) The set of all N × N invertible matrices with the group operation of matrix multiplication forms the General Linear Group of dimension N. This group is denoted by the symbol GL(N), or GL(N, K) where K is a field, such as R, C, etc. Generally, we will only consider the cases where K = R or K = C, which are respectively denoted by GL(N, R) and GL(N, C).
    [Show full text]
  • Matrix Multiplication. Diagonal Matrices. Inverse Matrix. Matrices
    MATH 304 Linear Algebra Lecture 4: Matrix multiplication. Diagonal matrices. Inverse matrix. Matrices Definition. An m-by-n matrix is a rectangular array of numbers that has m rows and n columns: a11 a12 ... a1n a21 a22 ... a2n . .. . am1 am2 ... amn Notation: A = (aij )1≤i≤n, 1≤j≤m or simply A = (aij ) if the dimensions are known. Matrix algebra: linear operations Addition: two matrices of the same dimensions can be added by adding their corresponding entries. Scalar multiplication: to multiply a matrix A by a scalar r, one multiplies each entry of A by r. Zero matrix O: all entries are zeros. Negative: −A is defined as (−1)A. Subtraction: A − B is defined as A + (−B). As far as the linear operations are concerned, the m×n matrices can be regarded as mn-dimensional vectors. Properties of linear operations (A + B) + C = A + (B + C) A + B = B + A A + O = O + A = A A + (−A) = (−A) + A = O r(sA) = (rs)A r(A + B) = rA + rB (r + s)A = rA + sA 1A = A 0A = O Dot product Definition. The dot product of n-dimensional vectors x = (x1, x2,..., xn) and y = (y1, y2,..., yn) is a scalar n x · y = x1y1 + x2y2 + ··· + xnyn = xk yk . Xk=1 The dot product is also called the scalar product. Matrix multiplication The product of matrices A and B is defined if the number of columns in A matches the number of rows in B. Definition. Let A = (aik ) be an m×n matrix and B = (bkj ) be an n×p matrix.
    [Show full text]
  • Linear Transformations and Determinants Matrix Multiplication As a Linear Transformation
    Linear transformations and determinants Math 40, Introduction to Linear Algebra Monday, February 13, 2012 Matrix multiplication as a linear transformation Primary example of a = matrix linear transformation ⇒ multiplication Given an m n matrix A, × define T (x)=Ax for x Rn. ∈ Then T is a linear transformation. Astounding! Matrix multiplication defines a linear transformation. This new perspective gives a dynamic view of a matrix (it transforms vectors into other vectors) and is a key to building math models to physical systems that evolve over time (so-called dynamical systems). A linear transformation as matrix multiplication Theorem. Every linear transformation T : Rn Rm can be → represented by an m n matrix A so that x Rn, × ∀ ∈ T (x)=Ax. More astounding! Question Given T, how do we find A? Consider standard basis vectors for Rn: Transformation T is 1 0 0 0 completely determined by its . e1 = . ,...,en = . action on basis vectors. 0 0 0 1 Compute T (e1),T(e2),...,T(en). Standard matrix of a linear transformation Question Given T, how do we find A? Consider standard basis vectors for Rn: Transformation T is 1 0 0 0 completely determined by its . e1 = . ,...,en = . action on basis vectors. 0 0 0 1 Compute T (e1),T(e2),...,T(en). Then || | is called the T (e ) T (e ) T (e ) 1 2 ··· n standard matrix for T. || | denoted [T ] Standard matrix for an example Example x 3 2 x T : R R and T y = → y z 1 0 0 1 0 0 T 0 = T 1 = T 0 = 0 1 0 0 0 1 100 2 A = What is T 5 ? 010 − 12 2 2 100 2 A 5 = 5 = ⇒ − 010− 5 12 12 − Composition T : Rn Rm is a linear transformation with standard matrix A Suppose → S : Rm Rp is a linear transformation with standard matrix B.
    [Show full text]