DOCSLIB.ORG

Downloaded from the Websites of Their Respective Developers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Downloaded from the Websites of Their Respective Developers http://researchspace.auckland.ac.nz ResearchSpace@Auckland Copyright Statement The digital copy of this thesis is protected by the Copyright Act 1994 (New Zealand). This thesis may be consulted by you, provided you comply with the provisions of the Act and the following conditions of use: • Any use you make of these documents or images must be for research or private study purposes only, and you may not make them available to any other person. • Authors control the copyright of their thesis. You will recognise the author's right to be identified as the author of this thesis, and due acknowledgement will be made to the author where appropriate. • You will obtain the author's permission before publishing any material from their thesis. To request permissions please use the Feedback form on our webpage. http://researchspace.auckland.ac.nz/feedback General copyright and disclaimer In addition to the above conditions, authors give their consent for the digital copy of their work to be used subject to the conditions specified on the Library Thesis Consent Form and Deposit Licence. Using a Hybrid Model for Investigating Residential Segregation: An Empirical and Simulation-based Study Babak Mahdavi Ardestani A thesis submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy The University of Auckland 2013 Abstract The impact of residential segregation on the dynamics of spatial, social and economic spheres of society is a topic of great interest in geography, sociology and economics. Residential segregation and its spatial separation effects have been acknowledged as having significant impacts on education, healthcare, business as well as social network and social/ urban structures. The complexity and multidimensional nature of the residential segregation phenomenon and the centrality of the individual based decision making process made this topic an ideal case for investigation using a micro/ individual based simulation modelling approach. An example of such an approach is agent‐based modelling (ABM) as theorised by Thomas Schelling. However, most Schelling‐type models are often too simple and small. This lack of sophistication and ‘small‐village’ syndrome remain though among the major weak points of existing models generally. More importantly, the lack of empirical support for informing and verification has long impeded the widespread acceptance of most simulation modelling approaches of this kind. Various individual based simulation modelling approaches to investigate residential segregation are reviewed. In particular, two simulation modelling approaches – agent‐based modelling (ABM) and microsimulation (MSM) – are compared with the aim of embracing a combined design approach that will also include key features of geosimulation models. For this reason a series of model prototypes are built initially to examine different aspects of a combined design approach, and with consideration of available census data (in aggregate format), the HAAMoS model is ultimately presented. It can simulate the entire population of the Auckland metropolitan area whilst dealing with up to four major ethnic groups each of which exhibit heterogeneous behaviours and have multi‐level preferences. It can also measure various dimensions of segregation, including local and spatially sensitive ones at different geographical scales. The implementation of these features is described. A descriptive statistical analysis of the modified data describes past and present patterns of residential location by ethnicity in the Auckland region area, which in turn ii are used as ‘benchmarks’ against the model’s outputs. Using specific scenarios, it is demonstrated that this relatively simple Schelling‐type model – informed by empirical data – has the potential to replicate plausible residential distribution patterns, even though the detailed representation of decision making behaviours are not available/ used. This demonstration confirms that the development of a potential ‘test‐bed’ consisting of an agent‐based model using census data for future modelling‐based research which can address residential and socio‐spatial segregation questions and similar theoretical issues in urban geography, sociology or economics would be feasible. The methodological approaches built and used in this research are among its important achievements. Further possible extensions of this research under different topics are also discussed. iii World is a lunatic sphere, Donʹt always agree itʹs real, Even with my feet upon it, […], My address is somewhere else. – (Hafez, Persian poet) In memory of Suri Anisi For Penney & Aryana with love iv Acknowledgments As with any project with this magnitude, debts of gratitude are accumulated along the way. Many people deserve a vote of thanks for their inspiration, support and encouragement over the duration of this project. Special mention must go to my supervisors, Professors David O’Sullivan and Peter Davis, for their invaluable advice, insights, guidance, support, endurance and patience. Each of them contributed a unique perspective that shaped the direction of this research work, whilst also proving willing to give me a free hand to build a unique modelling framework and to bring the thesis to a successful conclusion. Numerous collaborators, colleagues and friends have also given me much needed support at each stage of the process of pursuing this degree. I am therefore indebted to each of them. Alan Kwok Lun Cheung was instrumental in helping me with GIS related issues and questions. Roy Lay‐Yee and Lyndon Walker were also helpful in many different ways throughout this research study. Mark Whelden and Martin von Randow helped me with the SNZ datalab issues and related SAS inquiries. Many people provided me with instructive feedbacks, encouragement or simulating thoughts and discussions during or after seminars and meetings. Thanks are due to Alastair Scott, Alan Lee, Gordon Winder, Ward Friesen, and George Perry. I would also like to thank previous and current COMPASS Research Centre associates, collaborators, and colleagues. These include Daniel Patrick, Katharina Bauer, Gerry Cotterell, Mervyl McPherson, Janet Pearson, and Rocio Gomez. Special thanks goes to my postgraduate and undergraduate teachers, advisors and mentors, Professors Monty Newborn, Nelly Khouzam, and Dimitri Vouliouris who always believed in me and did not hesitate to support me. The self‐imposed desire to live up to the trust, hopes, and expectations of others is indeed a powerful incentive. I also extend a special word of thanks to Steve MacDonell and Andy Connor for their insights and generosity. v I must also acknowledge the Royal Society of New Zealand’s Marsden Fund for their research funding of this project. Finally, I would like to dedicate this thesis to the soul of my mother and to my wonderful wife Penney and my sweet and brilliant daughter Aryana, for their support, love, sacrifice, and encouragement which has enabled me to achieve this academic accomplishment. vi Contents List of Figures ........................................................................................................................... xi List of Tables .......................................................................................................................... xiii 1. Introduction ............................................................................................................................ 1 1.1 Overview ........................................................................................................................... 1 1.1 Research Components and Their Relationships ..................................................... 4 1.2 Motivations ....................................................................................................................... 5 1.3 Research Hypotheses ...................................................................................................... 6 1.4 Research Aims and Objectives ....................................................................................... 7 1.5 Research Approach .......................................................................................................... 8 1.6 Specific Research Questions ......................................................................................... 10 1.7 Organisation of the Thesis ............................................................................................ 11 2. Background .......................................................................................................................... 13 2.1 Introduction .................................................................................................................... 13 2.2 Residential Segregation ................................................................................................. 13 2.2.1 The Importance of Residential Segregation ........................................................ 15 2.2.2 Complexity and Determinants of Residential Segregation .............................. 16 2.2.3 Emergence and Self‐organisation of Residential Segregation .......................... 17 2.2.4 Explanatory Factors ................................................................................................ 19 2.2.5 Operationalizing Neighbourhood Characteristics ............................................. 21 2.2.6 Thesis Focus on Selective Factors ......................................................................... 21 2.3 Modelling Residential
Load more

Recommended publications
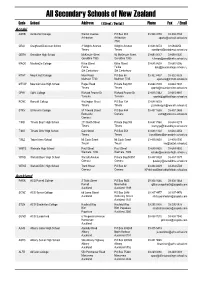
  • Secondary Schools of New Zealand
    All Secondary Schools of New Zealand Code School Address ( Street / Postal ) Phone Fax / Email Aoraki ASHB Ashburton College Walnut Avenue PO Box 204 03-308 4193 03-308 2104 Ashburton Ashburton [email protected] 7740 CRAI Craighead Diocesan School 3 Wrights Avenue Wrights Avenue 03-688 6074 03 6842250 Timaru Timaru [email protected] GERA Geraldine High School McKenzie Street 93 McKenzie Street 03-693 0017 03-693 0020 Geraldine 7930 Geraldine 7930 [email protected] MACK Mackenzie College Kirke Street Kirke Street 03-685 8603 03 685 8296 Fairlie Fairlie [email protected] Sth Canterbury Sth Canterbury MTHT Mount Hutt College Main Road PO Box 58 03-302 8437 03-302 8328 Methven 7730 Methven 7745 [email protected] MTVW Mountainview High School Pages Road Private Bag 907 03-684 7039 03-684 7037 Timaru Timaru [email protected] OPHI Opihi College Richard Pearse Dr Richard Pearse Dr 03-615 7442 03-615 9987 Temuka Temuka [email protected] RONC Roncalli College Wellington Street PO Box 138 03-688 6003 Timaru Timaru [email protected] STKV St Kevin's College 57 Taward Street PO Box 444 03-437 1665 03-437 2469 Redcastle Oamaru [email protected] Oamaru TIMB Timaru Boys' High School 211 North Street Private Bag 903 03-687 7560 03-688 8219 Timaru Timaru [email protected] TIMG Timaru Girls' High School Cain Street PO Box 558 03-688 1122 03-688 4254 Timaru Timaru [email protected] TWIZ Twizel Area School Mt Cook Street Mt Cook Street
    [Show full text]
  • REFERENCE LIST: 10 (4) Legat, Nicola
    REFERENCE LIST: 10 (4) Legat, Nicola. "South - the Endurance of the Old, the Shock of the New." Auckland Metro 5, no. 52 (1985): 60-75. Roger, W. "Six Months in Another Town." Auckland Metro 40 (1984): 155-70. ———. "West - in Struggle Country, Battlers Still Triumph." Auckland Metro 5, no. 52 (1985): 88-99. Young, C. "Newmarket." Auckland Metro 38 (1984): 118-27. 1 General works (21) "Auckland in the 80s." Metro 100 (1989): 106-211. "City of the Commonwealth: Auckland." New Commonwealth 46 (1968): 117-19. "In Suburbia: Objectively Speaking - and Subjectively - the Best Suburbs in Auckland - the Verdict." Metro 81 (1988): 60-75. "Joshua Thorp's Impressions of the Town of Auckland in 1857." Journal of the Auckland Historical Society 35 (1979): 1-8. "Photogeography: The Growth of a City: Auckland 1840-1950." New Zealand Geographer 6, no. 2 (1950): 190-97. "What’s Really Going On." Metro 79 (1988): 61-95. Armstrong, Richard Warwick. "Auckland in 1896: An Urban Geography." M.A. thesis (Geography), Auckland University College, 1958. Elphick, J. "Culture in a Colonial Setting: Auckland in the Early 1870s." New Zealand Journal of Educational Studies 10 (1974): 1-14. Elphick, Judith Mary. "Auckland, 1870-74: A Social Portrait." M.A. thesis (History), University of Auckland, 1974. Fowlds, George M. "Historical Oddments." Journal of the Auckland Historical Society 4 (1964): 35. Halstead, E.H. "Greater Auckland." M.A. thesis (Geography), Auckland University College, 1934. Le Roy, A.E. "A Little Boy's Memory of Auckland, 1895 to Early 1900." Auckland-Waikato Historical Journal 51 (1987): 1-6. Morton, Harry.
    [Show full text]
  • From Urban Sprawl to Compact City – an Analysis of Urban Growth Management in Auckland
    From Urban Sprawl to Compact City – An analysis of urban growth management in Auckland Joshua Arbury For my daughter Amalia - 1 - Acknowledgements: I would like to thank everyone who participated in the questionnaires and interviews, my supervisor Ward Friesen for providing useful insights and helpful suggestions, and particularly my mother, Jacquelyn Arbury, for her priceless help with proof-reading and editing. - 2 - Contents Title 1 Acknowledgements 2 Contents 3 List of Figures 5 Chapter One – Introduction 7 Chapter Two – Urban Sprawl versus the Compact City 14 2.1 Introduction 15 2.2 The rise of Urban Sprawl 18 2.3 Sustainability and Sprawl 29 2.4 The Compact City 44 2.5 Critiques of the Compact City 54 2.6 New Approaches and a Focus on Urban Design 58 2.7 Conclusions 63 Chapter Three – The Auckland Region: Problems and Responses 66 3.1 Introduction 67 3.2 A History of Auckland’s Growth 69 3.3 The Auckland Regional Growth Strategy 74 3.4 Implementing the Strategy 89 3.5 Critiquing the Regional Growth Strategy 96 3.6 Conclusions 101 Chapter Four – Implementing the Regional Growth Strategy in Auckland City: creating ‘Transit-Oriented Developments’ 104 4.1 Introduction 105 4.2 A ‘Growth Management Strategy’ for Auckland City 107 4.3 Transit-Oriented Developments 118 4.4 Conclusions 125 Chapter Five – Avondale’s Future 127 5.1 Introduction 128 - 3 - 5.2 A Brief History of Avondale 129 5.3 A ‘Liveable Community Plan’ for ‘Avondale’s Future’ 135 5.4 Visual Interpretation of Avondale’s Capacity for Growth 143 5.5 Questionnaire and Interview Results 149 5.6 Conclusions 157 Chapter Six – Conclusions 159 References 165 - 4 - List of Figures Figure 2.1: The effect of evolving transportation technologies on city form Figure 2.2: The evolving distance of a one hour commute Photo 2.1: The spatially extensive and automobile dependent urban sprawl Table 3.1: Desired regional outcomes to be achieved in a Regional Growth Strategy Table 3.2: Principles that will need to be applied to achieve desired outcomes Photo 3.1: An example of Residential 8b zone.
    [Show full text]
  • Consultation on Te Whau Pathway Your Feedback
    Consultation on Te Whau Pathway Your feedback Contents Summary ................................................................................................................... 2 Key themes in feedback ................................................................................................... 2 Next steps ........................................................................................................................ 4 Background .............................................................................................................. 5 Project information............................................................................................................ 5 Consultation ............................................................................................................. 6 Consultation activities ....................................................................................................... 6 Feedback form ................................................................................................................. 7 Feedback ................................................................................................................... 8 Analysis of your feedback ................................................................................................. 8 What you like about the pathway ......................................................................... 8 What you would change about the pathway, and issues you foresee................ 12 Comments and suggestions .............................................................................
    [Show full text]
  • THE HISTORY of the WHAU Estalished in Queen Mary Avenue in 1893
    In the Beginning: Pre-1800s Early Maori Settlement The 1800s: First European Settlement & Beginning of Industry The Early 1900s The late 1980s Today Future Infill Houding The Original Subdivision of Avondale Into Allotments Laurie’s brickyard, 1900 Glendene, 1938; the end of Hepburn Road, cen- tre. Span Farm to the left. Major Transport Route for Maori More And More Industries Near The River The Scow “Rahiri” Typical early brickyard with barges on the Whau, Today’s River circa 1912 The Great North Road, 1870 Te Whau Point 1880s Te Whau Point 1890s Picnic Spot Friends of the Whau Inc. 1999 In 1890, there were only 29 buildings in the New Lynn Borough and most of the surrounding area was farmland. By 1996, the census records n 1845 the Great North Road was laid out in 64,000 people living in the catchment, in almost response to the threat of attack on Auckland by Along the riverbank and harbour coastlines, Maori cultivated food and 22,000 households. Since 1996, people have northland Maori. Initially following New North gathered kai moana, the many shell middens found there today a In the early 1840’s the whole of the Auckland continued to move into the area. To meet the In earlier times, Maori used the Whau for travel between the Waitemata Harbour For most of last century, New Lynn was famous Road as far as Rocky Nook, it then continued reminder of that time. Their scared places (waahi tapu) and pa sites area was declared to be the country of Eden. By the early 1900’s most Avondale and New Lynn population growth, more houses have been built (on the Pacific east coast) and the Manukau Harbour (on the Tasman west for making bricks using the heavy soils as the along Western Springs Road to the present Great also left an imprint on the land, including the pa site at the headland in Pakeha also discovered the joys of this This country was divided into a number of brickyards were situated closed to the railway line.
    [Show full text]
  • Appendix 3A Schedule of Archaeological Features
    APPENDIX 3A SCHEDULE OF ARCHAEOLOGICAL FEATURES . CITY OF AUCKLAND - DISTRICT PLAN ISTHMUS SECTION - OPERATIVE 1999 Page 1 reprinted 04/07/03 APPENDIX 3A CITY OF AUCKLAND - DISTRICT PLAN Page 2 ISTHMUS SECTION - OPERATIVE 1999 reprinted 04/07/03 APPENDIX 3A SCHEDULE OF ARCHAEOLOGICAL FEATURES Note: A = Archaeological Feature H = Historic/Cultural Value A/G = Archaeological and Geological Feature S = Scientific/Educational Value V = Visual Amenity Value For an explanation of the criteria for scheduling and the rules refer Part 5C.7.4 ARCHAEOLOGICAL FEATURES NOTE: This schedule is not the same as the New Zealand Historic Places Trust Register for Auckland. It is a separate but parallel protection process. Since an archaeological feature may appear in either or both lists care should be taken to ascertain and fulfil any obligations deriving from the feature being included in either or both lists. THIS SCHEDULE DOES NOT INCLUDE PROTECTED ITEMS IN THE CENTRAL AREA OR HAURAKI GULF ISLANDS ADDRESS FEATURE PRINCIPAL FEATURE MAP CRITERIA FOR TYPE REFERENCE SCHEDULING Achilles Point to Karaka Bay cliffline Pa and associated Maori H, S, V A/G B15-06 Cliff Road, Waitara Road, Riddell Road habitation sites. Waitemata vicinity. series sandstone cliffs showing folded strata and Parnell Grit at Karaka Point. Also fallen blocks from the tuff ring of Glover Park. Crater containing pieces of greywacke, sandstone and schist brought up from depth Auckland Domain Pa and associated Maori H, S, V A/G C09-23 Stanley Street, Titoki Street, Carlton Gore habitation sites, early European Road, Park Road, Auckland Hospital, sites, explosion crater, scoria Grafton Road.
    [Show full text]
  • Oia-1156529-SMS-Systems.Pdf
    School Number School Name SMSInfo 3700 Abbotsford School MUSAC edge 1680 Aberdeen School eTAP 2330 Aberfeldy School Assembly SMS 847 Academy for Gifted Education eTAP 3271 Addington Te Kura Taumatua Assembly SMS 1195 Adventure School MUSAC edge 1000 Ahipara School eTAP 1200 Ahuroa School eTAP 82 Aidanfield Christian School KAMAR 1201 Aka Aka School MUSAC edge 350 Akaroa Area School KAMAR 6948 Albany Junior High School KAMAR ACT 1202 Albany School eTAP 563 Albany Senior High School KAMAR 3273 Albury School MUSAC edge 3701 Alexandra School LINC-ED 2801 Alfredton School MUSAC edge 6929 Alfriston College KAMAR 1203 Alfriston School eTAP 1681 Allandale School eTAP 3274 Allenton School Assembly SMS 3275 Allenvale Special School and Res Centre eTAP 544 Al-Madinah School MUSAC edge 3276 Amberley School MUSAC edge 614 Amesbury School eTAP 1682 Amisfield School MUSAC edge 308 Amuri Area School INFORMATIONMUSAC edge 1204 Anchorage Park School eTAP 3703 Andersons Bay School Assembly SMS 683 Ao Tawhiti Unlimited Discovery KAMAR 2332 Aokautere School eTAP 3442 Aoraki Mount Cook School MUSAC edge 1683 Aorangi School (Rotorua) MUSAC edge 96 Aorere College KAMAR 253 Aotea College KAMAR 1684 Apanui School eTAP 409 AparimaOFFICIAL College KAMAR 2333 Apiti School MUSAC edge 3180 Appleby School eTAP 482 Aquinas College KAMAR 1206 THEArahoe School MUSAC edge 2334 Arahunga School eTAP 2802 Arakura School eTAP 1001 Aranga School eTAP 2336 Aranui School (Wanganui) eTAP 1002 Arapohue School eTAP 1207 Ararimu School MUSAC edge 1686 Arataki School MUSAC edge 3704
    [Show full text]
  • Imagine the Land Ekarasa Doblanovic in Association with Age Concern and Lynfield College
    IMAGINE THE LAND EKARASA DOBLANOVIC IN ASSOCIATION WITH AGE CONCERN AND LYNFIELD COLLEGE Over 100 participants made pitch clay bowls which form a carpet of collective imagination you see today. Imagine the Land is a celebration of local Ekarasa Doblanovic materials, creativity and inter-generational is an Italian/Croatian- sharing, building a connection to place and born, New Zealand fostering ongoing creative relationships. artist. She received It puts locally-sourced clay and clay a Master of Fine pigments into the hands of the Blockhouse Arts (Honours) in Bay and Lynfield communities, students Visual Arts from Auckland University of and older people, inviting them to craft Technology in 2014. Her creative practice bowls together and imagine futures of encompasses painting and installation creativity, care and respect. with solo shows and many similar Imagine the Land collaborative and participatory Students from Lynfield College and projects across New Zealand and residents from Donovan Village Australia. She is an active ambassador participated in a series of interactive for Michelangelo Pisteletto’s Third workshops where they crafted hundreds Paradise Project. Her work investigates of clay bowls. Students generated the collaborative and participatory where a collective poem reflecting on the notions of space, ecology, impermanence encounter, facilitated by poet Gus and human interactions are explored to Simonovic. Raymond Sagapolutele create empathic dialogue amongst people, (photography) and Lynfield College art and nature. student
    [Show full text]
  • All Auckland Secondary Schools
    All Auckland Secondary Schools 27-Jan-2017 School Code Principal Phone Address ( Street / Postal ) ACG Parnell College PARN Ed Coup 09-308 1666 2 Titoki Street PO Box 9825 Parnell Newmarket Auckland Auckland 1149 ACG Senior College SCNZ Graham Gottard 09-307 4477 66 Lorne Street PO Box 5646 Auckland Wellesley Street Auckland 1141 ACG Strathallan College STLN Robin Kirkham 09-295 0830 Hayfield Way Hayfield Way RD1 RD1 Papakura Papakura Auckland 2580 ACG Sunderland SUND Nathan Villars 09-838 7070 6 Waipereira Avenue Henderson Auckland Albany Junior High School AJHS Stephen Kendall- 09-415 5473 Appleby Road PO Box 303269 Jones Albany North Harbour Auckland Auckland 0751 Albany Senior High School ASHS Barbara Cavanagh 09-451 9065 536 Albany Highway PO Box 300380 Albany Albany Auckland Auckland 0752 Alfriston College ALFR Rob Solomone 09-269 0080 550 Porchester Road PO Box 75448 Manurewa Manurewa Auckland Auckland 2243 Al-Madinah School ALMA Asin Ali 09-275 5195 8 Westney Road PO Box 43246 Mangere Mangere Auckland Auckland 2153 Aorere College AORE Gregory Pierce 09-278 5608 Portage Road PO Box 23084 Papatoetoe Hunters Corner Auckland Manukau Auckland 2155 Auckland Girls Grammar School AGGS Ngaire Ashmore 09-307 4180 16 Howe Street PO Box 68053 Newton Newton Auckland Auckland 1145 Auckland Grammar School AGSB Tim O'Connor 09-623 5400 Mountain Road Pte Bag 99930 Epsom Newmarket Auckland Auckland 1149 Auckland International College AKLI Carolyn Solomon 09-309 4480 37 Heaphy Street PO Box 3966 Blockhouse Bay Shortland Street Auckland Auckland
    [Show full text]
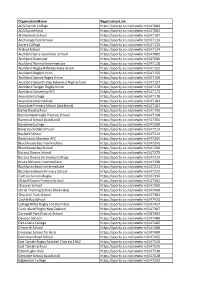
  • Organisationname
    OrganisationName RegistrationLink ACG Parnell College https://sporty.co.nz/viewform/147080 ACG Sunderland https://sporty.co.nz/viewform/147081 Al-Madinah School https://sporty.co.nz/viewform/147107 Anchorage Park School https://sporty.co.nz/viewform/147116 Aorere College https://sporty.co.nz/viewform/147123 Arahoe School https://sporty.co.nz/viewform/147134 Auckland Girls' Grammar School https://sporty.co.nz/viewform/147085 Auckland Grammar https://sporty.co.nz/viewform/147086 Auckland Normal Intermediate https://sporty.co.nz/viewform/147118 Auckland Rugby Referees Association https://sporty.co.nz/viewform/147152 Auckland Rugby Union https://sporty.co.nz/viewform/147156 Auckland Samoa Rugby Union https://sporty.co.nz/viewform/147169 Auckland Seventh-Day Adventist High School https://sporty.co.nz/viewform/147157 Auckland Tongan Rugby Union https://sporty.co.nz/viewform/147170 Auckland University RFC https://sporty.co.nz/viewform/147171 Avondale College https://sporty.co.nz/viewform/147178 Avondale Intermediate https://sporty.co.nz/viewform/147181 Avondale Primary School (Auckland) https://sporty.co.nz/viewform/147182 Bailey Road School https://sporty.co.nz/viewform/147196 Bairds Mainfreight Primary School https://sporty.co.nz/viewform/147198 Balmoral School (Auckland) https://sporty.co.nz/viewform/147204 Baradene College https://sporty.co.nz/viewform/147209 Baverstock Oaks School https://sporty.co.nz/viewform/147213 Bayfield School https://sporty.co.nz/viewform/147214 Beachlands Maraetai AFC https://sporty.co.nz/viewform/147265 Blockhouse
    [Show full text]
  • Unitary Plan Appeal Decision No. 2016
    IN THE HIGH COURT OF NEW ZEALAND AUCKLAND REGISTRY CIV-2016-404-2336 [2016] NZHC 138 BETWEEN ALBANY NORTH LANDOWNERS Plaintiff AND AUCKLAND COUNCIL Defendant [Continued over page] Hearing: 28 November - 2 December 2016 Counsel: M Baker-Galloway for Albany North Landowers T Mullins for Auckland Memorial Park Ltd S Ryan for Franco Belgiorno-Nettis R Brabant and R Enright for Character Coalition Inc & Anor M Savage for Howick Ratepayers and Residents Assoc Inc & Anor R Enright for The Straits Protection Society Inc and South Epsom Planning Group Inc & Anor A A Arthur-Young and S H Pilkington for Strand Holdings Ltd R E Bartlett QC for Summerset Group Holdings Ltd A A Arthur-Young and D J Minhinnick for Valerie Close Residents Group H Atkins for Village New Zealand Ltd R Brabant for Wallace Group Ltd M Casey QC and M Williams for Man OʼWar Farm Ltd R J Somerville QC, K Anderson and W G Wakefield for Auckland Council C Kirman and A Devine for Housing Corporation New Zealand and Minister for the Enironment S F Quinn and A F Buchanan for Ting Holdings Ltd S J Simons and R M Steller for Property Council of New Zealand R M Devine for Ngati Whatua Orakei Whai Rawa Ltd Judgment: 13 February 2017 JUDGMENT OF WHATA J ALBANY NORTH LANDOWNERS v AUCKLAND COUNCIL [2016] NZHC 138 [13 February 2017] This judgment was delivered by me on 13 February 2017 at 11.30 am, pursuant to Rule 11.5 of the High Court Rules. Registrar/Deputy Registrar Date: ………………………… CIV-2016-404-2298 BETWEEN AUCKLAND MEMORIAL PARK LIMITED Plaintiff AND AUCKLAND COUNCIL Defendant CIV-2016-404-2323
    [Show full text]
  • School Number (Moe)
    School Roll Count Regional Council (MoE (MoE) Name School Type Authority Intiative Number (Nov 15) Data) 1606 ACG New Zealand International College Secondary (Year 9-15) 872 Private: Fully Reg. Auckland Region Chorus UFB 2085 ACG Parnell College Composite (Year 1-15) 797 Private: Fully Reg. Auckland Region Chorus UFB 1605 ACG Senior College Secondary (Year 9-15) 242 Private: Fully Reg. Auckland Region Chorus UFB 441 ACG Strathallan Composite (Year 1-15) 912 Private: Fully Reg. Auckland Region Chorus RBI 571 ACG Sunderland Composite (Year 1-15) 316 Private: Fully Reg. Auckland Region Chorus UFB 1200 Ahuroa School Full Primary (Year 1-8) 77 State: Not integrated Auckland Region Chorus RBI 6948 Albany Junior High School Secondary (Year 7-10) 1146 State: Not integrated Auckland Region Chorus UFB 1202 Albany School Contributing (Year 1-6) 670 State: Not integrated Auckland Region Chorus UFB 563 Albany Senior High School Secondary (Year 11-15) 731 State: Not integrated Auckland Region Chorus UFB 6929 Alfriston College Secondary (Year 9-15) 1332 State: Not integrated Auckland Region Chorus UFB 1203 Alfriston School Full Primary (Year 1-8) 333 State: Not integrated Auckland Region Chorus RBI 544 Al-Madinah School Composite (Year 1-15) 528 State: Integrated Auckland Region Chorus UFB 462 Ambury Park Centre for Riding Therapy Secondary (Year 9-15) 50 Private: Fully Reg. Auckland Region Chorus UFB 1204 Anchorage Park School Contributing (Year 1-6) 157 State: Not integrated Auckland Region Chorus UFB 96 Aorere College Secondary (Year 9-15) 1467 State:
    [Show full text]