Coordinate Systems and Examples of the Chain Rule Alex Nita
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Anti-Chain Rule Name
Anti-Chain Rule Name: The most fundamental rule for computing derivatives in calculus is the Chain Rule, from which all other differentiation rules are derived. In words, the Chain Rule states that, to differentiate f(g(x)), differentiate the outside function f and multiply by the derivative of the inside function g, so that d f(g(x)) = f 0(g(x)) · g0(x): dx The Chain Rule makes computation of nearly all derivatives fairly easy. It is tempting to think that there should be an Anti-Chain Rule that makes antidiffer- entiation as easy as the Chain Rule made differentiation. Such a rule would just reverse the process, so instead of differentiating f and multiplying by g0, we would antidifferentiate f and divide by g0. In symbols, Z F (g(x)) f(g(x)) dx = + C: g0(x) Unfortunately, the Anti-Chain Rule does not exist because the formula above is not Z always true. For example, consider (x2 + 1)2 dx. We can compute this integral (correctly) by expanding and applying the power rule: Z Z (x2 + 1)2 dx = x4 + 2x2 + 1 dx x5 2x3 = + + x + C 5 3 However, we could also think about our integrand above as f(g(x)) with f(x) = x2 and g(x) = x2 + 1. Then we have F (x) = x3=3 and g0(x) = 2x, so the Anti-Chain Rule would predict that Z F (g(x)) (x2 + 1)2 dx = + C g0(x) (x2 + 1)3 = + C 3 · 2x x6 + 3x4 + 3x2 + 1 = + C 6x x5 x3 x 1 = + + + + C 6 2 2 6x Since these answers are different, we conclude that the Anti-Chain Rule has failed us. -

9.2. Undoing the Chain Rule
< Previous Section Home Next Section > 9.2. Undoing the Chain Rule This chapter focuses on finding accumulation functions in closed form when we know its rate of change function. We’ve seen that 1) an accumulation function in closed form is advantageous for quickly and easily generating many values of the accumulating quantity, and 2) the key to finding accumulation functions in closed form is the Fundamental Theorem of Calculus. The FTC says that an accumulation function is the antiderivative of the given rate of change function (because rate of change is the derivative of accumulation). In Chapter 6, we developed many derivative rules for quickly finding closed form rate of change functions from closed form accumulation functions. We also made a connection between the form of a rate of change function and the form of the accumulation function from which it was derived. Rather than inventing a whole new set of techniques for finding antiderivatives, our mindset as much as possible will be to use our derivatives rules in reverse to find antiderivatives. We worked hard to develop the derivative rules, so let’s keep using them to find antiderivatives! Thus, whenever you have a rate of change function f and are charged with finding its antiderivative, you should frame the task with the question “What function has f as its derivative?” For simple rate of change functions, this is easy, as long as you know your derivative rules well enough to apply them in reverse. For example, given a rate of change function …. … 2x, what function has 2x as its derivative? i.e. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

A General Chain Rule for Distributional Derivatives
proceedings of the american mathematical society Volume 108, Number 3, March 1990 A GENERAL CHAIN RULE FOR DISTRIBUTIONAL DERIVATIVES L. AMBROSIO AND G. DAL MASO (Communicated by Barbara L. Keyfitz) Abstract. We prove a general chain rule for the distribution derivatives of the composite function v(x) = f(u(x)), where u: R" —>Rm has bounded variation and /: Rm —>R* is Lipschitz continuous. Introduction The aim of the present paper is to prove a chain rule for the distributional derivative of the composite function v(x) = f(u(x)), where u: Q —>Rm has bounded variation in the open set ilcR" and /: Rw —>R is uniformly Lip- schitz continuous. Under these hypotheses it is easy to prove that the function v has locally bounded variation in Q, hence its distributional derivative Dv is a Radon measure in Q with values in the vector space Jz? m of all linear maps from R" to Rm . The problem is to give an explicit formula for Dv in terms of the gradient Vf of / and of the distributional derivative Du . To illustrate our formula, we begin with the simpler case, studied by A. I. Vol pert, where / is continuously differentiable. Let us denote by Su the set of all jump points of u, defined as the set of all xef! where the approximate limit u(x) does not exist at x. Then the following identities hold in the sense of measures (see [19] and [20]): (0.1) Dv = Vf(ü)-Du onß\SH, and (0.2) Dv = (f(u+)-f(u-))®vu-rn_x onSu, where vu denotes the measure theoretical unit normal to Su, u+ , u~ are the approximate limits of u from both sides of Su, and %?n_x denotes the (n - l)-dimensional Hausdorff measure. -

Math 212-Lecture 8 13.7: the Multivariable Chain Rule
Math 212-Lecture 8 13.7: The multivariable chain rule The chain rule with one independent variable w = f(x; y). If the particle is moving along a curve x = x(t); y = y(t), then the values that the particle feels is w = f(x(t); y(t)). Then, w = w(t) is a function of t. x; y are intermediate variables and t is the independent variable. The chain rule says: If both fx and fy are continuous, then dw = f x0(t) + f y0(t): dt x y Intuitively, the total change rate is the superposition of contributions in both directions. Comment: You cannot do as in one single variable calculus like @w dx @w dy dw dw + = + ; @x dt @y dt dt dt @w by canceling the two dx's. @w in @x is only the `partial' change due to the dw change of x, which is different from the dw in dt since the latter is the total change. The proof is to use the increment ∆w = wx∆x + wy∆y + small. Read Page 903. Example: Suppose w = sin(uv) where u = 2s and v = s2. Compute dw ds at s = 1. Solution. By chain rule dw @w du @w dv = + = cos(uv)v ∗ 2 + cos(uv)u ∗ 2s: ds @u ds @v ds At s = 1, u = 2; v = 1. Hence, we have cos(2) ∗ 2 + cos(2) ∗ 2 ∗ 2 = 6 cos(2): We can actually check that w = sin(uv) = sin(2s3). Hence, w0(s) = 3 2 cos(2s ) ∗ 6s . At s = 1, this is 6 cos(2). -

Chapter 4 Differentiation in the Study of Calculus of Functions of One Variable, the Notions of Continuity, Differentiability and Integrability Play a Central Role
Chapter 4 Differentiation In the study of calculus of functions of one variable, the notions of continuity, differentiability and integrability play a central role. The previous chapter was devoted to continuity and its consequences and the next chapter will focus on integrability. In this chapter we will define the derivative of a function of one variable and discuss several important consequences of differentiability. For example, we will show that differentiability implies continuity. We will use the definition of derivative to derive a few differentiation formulas but we assume the formulas for differentiating the most common elementary functions are known from a previous course. Similarly, we assume that the rules for differentiating are already known although the chain rule and some of its corollaries are proved in the solved problems. We shall not emphasize the various geometrical and physical applications of the derivative but will concentrate instead on the mathematical aspects of differentiation. In particular, we present several forms of the mean value theorem for derivatives, including the Cauchy mean value theorem which leads to L’Hôpital’s rule. This latter result is useful in evaluating so called indeterminate limits of various kinds. Finally we will discuss the representation of a function by Taylor polynomials. The Derivative Let fx denote a real valued function with domain D containing an L ? neighborhood of a point x0 5 D; i.e. x0 is an interior point of D since there is an L ; 0 such that NLx0 D. Then for any h such that 0 9 |h| 9 L, we can define the difference quotient for f near x0, fx + h ? fx D fx : 0 0 4.1 h 0 h It is well known from elementary calculus (and easy to see from a sketch of the graph of f near x0 ) that Dhfx0 represents the slope of a secant line through the points x0,fx0 and x0 + h,fx0 + h. -

The Chain Rule in Partial Differentiation
THE CHAIN RULE IN PARTIAL DIFFERENTIATION 1 Simple chain rule If u = u(x, y) and the two independent variables x and y are each a function of just one other variable t so that x = x(t) and y = y(t), then to find du/dt we write down the differential of u ∂u ∂u δu = δx + δy + .... (1) ∂x ∂y Then taking limits δx 0, δy 0 and δt 0 in the usual way we have → → → du ∂u dx ∂u dy = + . (2) dt ∂x dt ∂y dt Note we only need straight ‘d’s’ in dx/dt and dy/dt because x and y are function of one variable t whereas u is a function of both x and y. 2 Chain rule for two sets of independent variables If u = u(x, y) and the two independent variables x, y are each a function of two new independent variables s, t then we want relations between their partial derivatives. 1. When u = u(x, y), for guidance in working out the chain rule, write down the differential ∂u ∂u δu = δx + δy + ... (3) ∂x ∂y then when x = x(s, t) and y = y(s, t) (which are known functions of s and t), the chain rule for us and ut in terms of ux and uy is ∂u ∂u ∂x ∂u ∂y = + (4) ∂s ∂x ∂s ∂y ∂s ∂u ∂u ∂x ∂u ∂y = + . (5) ∂t ∂x ∂t ∂y ∂t 2. Conversely, when u = u(s, t), for guidance in working out the chain rule write down the differential ∂u ∂u δu = δs + δt + .. -

Failure of the Chain Rule for the Divergence of Bounded Vector Fields
FAILURE OF THE CHAIN RULE FOR THE DIVERGENCE OF BOUNDED VECTOR FIELDS GIANLUCA CRIPPA, NIKOLAY GUSEV, STEFANO SPIRITO, AND EMIL WIEDEMANN ABSTRACT. We provide a vast class of counterexamples to the chain rule for the divergence of bounded vector fields in three space dimensions. Our convex integration approach allows us to produce renormalization defects of various kinds, which in a sense quantify the breakdown of the chain rule. For instance, we can construct defects which are absolutely continuous with respect to the Lebesgue measure, or defects which are not even measures. MSC (2010): 35F05 (PRIMARY); 35A02, 35Q35 KEYWORDS: Chain Rule, Convex Integration, Transport and Continuity Equations, Renormaliza- tion 1. INTRODUCTION In this paper we consider the classical problem of the chain rule for the divergence of a bounded vector field. Specifically, the problem can be stated in the following way: d d Let W ⊂ R be a domain with Lipschitz boundary. Given a bounded vector field v : W ! R tangent to the boundary and a bounded scalar function r : W ! R, one asks whether it is possible to express the quantity div(b(r)v), where b is a smooth scalar function, only in terms of b, r and the quantities m = divv and l = div(rv). Indeed, formally we should have that div(b(r)v) = (b(r) − rb 0(r))m + b 0(r)l: (1.1) However, the extension of (1.1) to a nonsmooth setting is far from trivial. The chain rule problem is particularly important in view of its applications to the uniqueness and compactness of transport and continuity equations, whose analysis is nowadays a fundamental tool in the study of various equations arising in mathematical physics. -

Chain Rule & Implicit Differentiation
INTRODUCTION The chain rule and implicit differentiation are techniques used to easily differentiate otherwise difficult equations. Both use the rules for derivatives by applying them in slightly different ways to differentiate the complex equations without much hassle. In this presentation, both the chain rule and implicit differentiation will be shown with applications to real world problems. DEFINITION Chain Rule Implicit Differentiation A way to differentiate A way to take the derivative functions within of a term with respect to functions. another variable without having to isolate either variable. HISTORY The Chain Rule is thought to have first originated from the German mathematician Gottfried W. Leibniz. Although the memoir it was first found in contained various mistakes, it is apparent that he used chain rule in order to differentiate a polynomial inside of a square root. Guillaume de l'Hôpital, a French mathematician, also has traces of the chain rule in his Analyse des infiniment petits. HISTORY Implicit differentiation was developed by the famed physicist and mathematician Isaac Newton. He applied it to various physics problems he came across. In addition, the German mathematician Gottfried W. Leibniz also developed the technique independently of Newton around the same time period. EXAMPLE 1: CHAIN RULE Find the derivative of the following using chain rule y=(x2+5x3-16)37 EXAMPLE 1: CHAIN RULE Step 1: Define inner and outer functions y=(x2+5x3-16)37 EXAMPLE 1: CHAIN RULE Step 2: Differentiate outer function via power rule y’=37(x2+5x3-16)36 EXAMPLE 1: CHAIN RULE Step 3: Differentiate inner function and multiply by the answer from the previous step y’=37(x2+5x3-16)36(2x+15x2) EXAMPLE 2: CHAIN RULE A biologist must use the chain rule to determine how fast a given bacteria population is growing at a given point in time t days later. -

Lecture 10 : Chain Rule (Please Review Composing Functions Under Algebra/Precalculus Review on the Class Webpage.) Here We Apply the Derivative to Composite Functions
Lecture 10 : Chain Rule (Please review Composing Functions under Algebra/Precalculus Review on the class webpage.) Here we apply the derivative to composite functions. We get the following rule of differentiation: The Chain Rule : If g is a differentiable function at x and f is differentiable at g(x), then the composite function F = f ◦ g defined by F (x) = f(g(x)) is differentiable at x and F 0 is given by the product F 0(x) = f 0(g(x))g0(x): In Leibniz notation If y = f(u) and u = g(x) are both differentiable functions, then dy dy du = : dx du dx It is not difficult to se why this is true, if we examine the average change in the value of F (x) that results from a small change in the value of x: F (x + h) − F (x) f(g(x + h)) − f(g(x)) f(g(x + h)) − f(g(x)) g(x + h) − g(x) = = · h h g(x + h) − g(x) h or if we let u = g(x) and y = F (x) = f(u), then ∆y ∆y ∆u = · ∆x ∆u ∆x if g(x + h) − g(x) = ∆u 6= 0. When we take the limit as h ! 0 or ∆x ! 0, we get F 0(x) = f 0(g(x))g0(x) or dy dy du = : dx du dx Example Find the derivative of F (x) = sin(2x + 1). Step 1: Write F (x) as F (x) = f(g(x)) or y = F (x) = f(u), where u = g(x). -
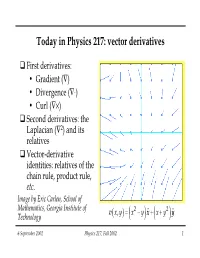
Today in Physics 217: Vector Derivatives
Today in Physics 217: vector derivatives First derivatives: • Gradient (—) • Divergence (—◊) •Curl (—¥) Second derivatives: the Laplacian (—2) and its relatives Vector-derivative identities: relatives of the chain rule, product rule, etc. Image by Eric Carlen, School of Mathematics, Georgia Institute of 22 vxyxy, =−++ x yˆˆ x y Technology ()()() 6 September 2002 Physics 217, Fall 2002 1 Differential vector calculus df/dx provides us with information on how quickly a function of one variable, f(x), changes. For instance, when the argument changes by an infinitesimal amount, from x to x+dx, f changes by df, given by df df= dx dx In three dimensions, the function f will in general be a function of x, y, and z: f(x, y, z). The change in f is equal to ∂∂∂fff df=++ dx dy dz ∂∂∂xyz ∂∂∂fff =++⋅++ˆˆˆˆˆˆ xyzxyz ()()dx() dy() dz ∂∂∂xyz ≡⋅∇fdl 6 September 2002 Physics 217, Fall 2002 2 Differential vector calculus (continued) The vector derivative operator — (“del”) ∂∂∂ ∇ =++xyzˆˆˆ ∂∂∂xyz produces a vector when it operates on scalar function f(x,y,z). — is a vector, as we can see from its behavior under coordinate rotations: I ′ ()∇∇ff=⋅R but its magnitude is not a number: it is an operator. 6 September 2002 Physics 217, Fall 2002 3 Differential vector calculus (continued) There are three kinds of vector derivatives, corresponding to the three kinds of multiplication possible with vectors: Gradient, the analogue of multiplication by a scalar. ∇f Divergence, like the scalar (dot) product. ∇⋅v Curl, which corresponds to the vector (cross) product. ∇×v 6 September 2002 Physics 217, Fall 2002 4 Gradient The result of applying the vector derivative operator on a scalar function f is called the gradient of f: ∂∂∂fff ∇f =++xyzˆˆˆ ∂∂∂xyz The direction of the gradient points in the direction of maximum increase of f (i.e. -

1. Antiderivatives for Exponential Functions Recall That for F(X) = Ec⋅X, F ′(X) = C ⋅ Ec⋅X (For Any Constant C)
1. Antiderivatives for exponential functions Recall that for f(x) = ec⋅x, f ′(x) = c ⋅ ec⋅x (for any constant c). That is, ex is its own derivative. So it makes sense that it is its own antiderivative as well! Theorem 1.1 (Antiderivatives of exponential functions). Let f(x) = ec⋅x for some 1 constant c. Then F x ec⋅c D, for any constant D, is an antiderivative of ( ) = c + f(x). 1 c⋅x ′ 1 c⋅x c⋅x Proof. Consider F (x) = c e +D. Then by the chain rule, F (x) = c⋅ c e +0 = e . So F (x) is an antiderivative of f(x). Of course, the theorem does not work for c = 0, but then we would have that f(x) = e0 = 1, which is constant. By the power rule, an antiderivative would be F (x) = x + C for some constant C. 1 2. Antiderivative for f(x) = x We have the power rule for antiderivatives, but it does not work for f(x) = x−1. 1 However, we know that the derivative of ln(x) is x . So it makes sense that the 1 antiderivative of x should be ln(x). Unfortunately, it is not. But it is close. 1 1 Theorem 2.1 (Antiderivative of f(x) = x ). Let f(x) = x . Then the antiderivatives of f(x) are of the form F (x) = ln(SxS) + C. Proof. Notice that ln(x) for x > 0 F (x) = ln(SxS) = . ln(−x) for x < 0 ′ 1 For x > 0, we have [ln(x)] = x .