Sovereign Risk Ratings' Country Classification Using Machine Learning
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Effective Credit Risk-Rating Systems
INTERNAL RISK RATINGS Credit Risk-Rating Systems by Tom Yu, Tom Garside, and Jim Stoker n this first of two articles, the authors describe the capabilities, desired attributes, and potential accruing benefits of effective credit risk-rating systems. The practical issues arising in an over- haul, the main theme of the second article, will be shown through a case study of one regional bank’s initiative to upgrade its credit risk man- agement process. redit risk ratings provide a models cannot be improved but portfolios. For corporate lending, common language for that the process of implementation credit scoring has been an impor- describing credit risk is challenging. Ratings are so tight- tant accelerator for securitization. exposure within an organization ly woven into the fabric of most and, increasingly, with parties out- institutions that they are part of the Justification for Change side the organization. As such, they culture. And any significant change A decade of advancements in drive a wide range of credit to the culture is difficult. quantitative measures of credit risk processes—from origination to However, the pressures to have led to better risk management monitoring to securitization to change are mounting from both at the transaction level as well as workout—and it is logical that bet- internal and external sources. the portfolio level. Lenders can ter credit risk ratings can lead to Internally, it may be the desire to actively manage their portfolio better credit risk management. Yet price loans more aggressively or to risks and returns relative to the many lenders are using ratings sys- support a more economically institution’s risk appetite and per- tems that were put in place 10 or attractive CLO structure. -

Company Presentation
ATRIUM – COMPANY PRESENTATION THE LEADING OWNER & MANAGER OF CENTRAL EASTERN EUROPEAN SHOPPING CENTRES May 2017 / Based on 2016 full-year results ATRIUM – LEADING OWNER & MANAGER OF CEE SHOPPING CENTRES A UNIQUE INVESTMENT OPPORTUNITY Strong management team with a proven track record Central European focus with dominant presence in the most mature & stable countries Robust balance sheet: 28.7% net LTV/ €104m cash Investment grade rating with a “Stable” outlook by Fitch and S&P Balance between solid income producing platform & opportunities for future growth KEY FIGURES 60 properties with a MV of c.€2.6bn and over 1.1 million m² GLA Focus on shopping centres, primarily food-anchored FY16 GRI: €195.8m, NRI: €188.8m Adjusted EPRA EPS: 31.4 €cents, EPRA NAV per share: €5.39* Special dividend of 14 €cents paid in September Board-approved dividend of 27 €cents per share for 2017**, dividend yield >11.5% Research coverage by Bank of America Merrill Lynch, Baader Bank, HSBC, Kempen, Raiffeisen and Wood & co * Including the special dividend. **Subject to any legal and regulatory requirements and restrictions of commercial viability All numbers in this presentation as reported in the 12M results to 31 December 2016 unless explicitly stated otherwise, incl. a 75% stake in Arkady Pankrac 2 FOCUS ON THE MOST MATURE AND STABLE MARKETS IN CEE 100% focus on Central and Eastern Europe (CEE) Poland, Czech Republic, Slovakia: 84% of MV/ 75% of NRI Exposure to investment-grade countries: 89%* 88% of 12M16 GRI is denominated in Euros, 6% in Polish Zlotys, 2% in Czech Korunas, 1% in USD and 3% in other currencies SLOVAKIA 3 POLAND RUSSIA 7 21 HUNGARY 22 ROMANIA GEOGRAPHIC MIX OF THE PORTFOLIO 1 11% 1618%% CentralCentral European European countries countries 5% (PL, CZ, SK) CZECH REP. -

Moody's Investor Service. Rating Symbols and Definitions
Rating Symbols and Definitions JANUARY 2011 MARCH 2008 Table of Contents Preface 2 Other Rating Services 29 Moody’s Standing Committee on Internal Ratings ...................................................................29 Rating Systems & Practices 3 Insured Ratings ...................................................................29 General Credit Rating Services 4 Enhanced Ratings ...............................................................29 Long-Term Obligation Ratings ............................................4 Underlying Ratings .............................................................29 Long-Term Issuer Ratings..................................................... 5 Other Rating Symbols 30 Hybrid Indicator (hyb) ......................................................... 5 Expected ratings - e ............................................................30 Medium-Term Note Program Ratings ............................... 5 Provisional Ratings - (P) .....................................................30 Short-Term Obligation Ratings ........................................... 5 Refundeds - # ......................................................................30 Short-Term Issuer Ratings ...................................................6 Withdrawn - WR .................................................................30 Sector Specific Credit Rating Services 7 Not Rated - NR ...................................................................30 US Municipal Short-Term Debt and Demand Not Available - NAV ...........................................................30 -

Fitch Ratings ING Groep N.V. Ratings Report 2020-10-15
Banks Universal Commercial Banks Netherlands ING Groep N.V. Ratings Foreign Currency Long-Term IDR A+ Short-Term IDR F1 Derivative Counterparty Rating A+(dcr) Viability Rating a+ Key Rating Drivers Support Rating 5 Support Rating Floor NF Robust Company Profile, Solid Capitalisation: ING Groep N.V.’s ratings are supported by its leading franchise in retail and commercial banking in the Benelux region and adequate Sovereign Risk diversification in selected countries. The bank's resilient and diversified business model Long-Term Local- and Foreign- AAA emphasises lending operations with moderate exposure to volatile businesses, and it has a Currency IDRs sound record of earnings generation. The ratings also reflect the group's sound capital ratios Country Ceiling AAA and balanced funding profile. Outlooks Pandemic Stress: ING has enough rating headroom to absorb the deterioration in financial Long-Term Foreign-Currency Negative performance due to the economic fallout from the coronavirus crisis. The Negative Outlook IDR reflects the downside risks to Fitch’s baseline scenario, as pressure on the ratings would Sovereign Long-Term Local- and Negative increase substantially if the downturn is deeper or more prolonged than we currently expect. Foreign-Currency IDRs Asset Quality: The Stage 3 loan ratio remained sound at 2% at end-June 2020 despite the economic disruption generated by the lockdowns in the countries where ING operates. Fitch Applicable Criteria expects higher inflows of impaired loans from 4Q20 as the various support measures mature, driven by SMEs and mid-corporate borrowers and more vulnerable sectors such as oil and gas, Bank Rating Criteria (February 2020) shipping and transportation. -
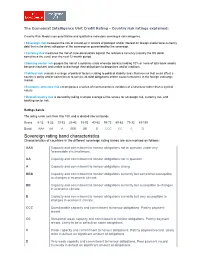
Sovereign Rating Band Characteristics Characteristics of Countries in the Different Sovereign Rating Bands Are Summarised As Follows
The Economist Intelligence Unit Credit Rating - Country risk ratings explained: Country Risk Model uses quantitative and qualitative indicators covering 6 risk categories. l Sovereign risk measures the risk of a build-up in arrears of principal and/or interest on foreign and/or local-currency debt that is the direct obligation of the sovereign or guaranteed by the sovereign. l Currency risk measures the risk of maxi-devaluation against the reference currency (usually the US dollar, sometimes the euro) over the next 12-month period. l Banking sector risk gauges the risk of a systemic crisis whereby bank(s) holding 10% or more of total bank assets become insolvent and unable to discharge their obligations to depositors and/or creditors. l Political risk evaluates a range of political factors relating to political stability and effectiveness that could affect a country’s ability and/or commitment to service its debt obligations and/or cause turbulence in the foreign exchange market. l Economic structure risk encompasses a series of macroeconomic variables of a structural rather than a cyclical nature. l Overall country risk is derived by taking a simple average of the scores for sovereign risk, currency risk, and banking sector risk. Ratings bands The rating scale runs from 0 to 100, and is divided into ten bands. Score 0-12 9-22 19-32 29-42 39-52 49-62 59-72 69-82 79-92 89-100 Band AAA AA A BBB BB B CCC CC C D Sovereign rating band characteristics Characteristics of countries in the different sovereign rating bands are summarised as follows: AAA Capacity and commitment to honour obligations not in question under any foreseeable circumstances. -

Report on the Activities of Credit Rating Agencies
REPORT ON THE ACTIVITIES OF CREDIT RATING AGENCIES THE TECHNICAL COMMITTEE OF THE INTERNATIONAL ORGANIZATION OF SECURITIES COMMISSIONS SEPTEMBER 2003 REPORT ON THE ACTIVITIES OF CREDIT RATING AGENCIES I. INTRODUCTION Credit rating agencies (CRAs) can play an important role in many domestic and cross- border transactions. CRAs assess the credit risk of corporate or government borrowers and issuers of fixed-income securities. CRAs attempt to make sense of the vast amount of information available regarding an issuer or borrower, its market and its economic circumstances in order to give investors and lenders a better understanding of the risks they face when lending to a particular borrower or when purchasing an issuer’s fixed-income securities.1 A credit rating, typically, is a CRA’s opinion of how likely an issuer is to repay, in a timely fashion, a particular debt or financial obligation, or its debts generally. Issuers, lenders, fixed-income investors, and government regulators use credit risk assessments for a variety of purposes. Issuers and corporate borrowers rely on (and, in many cases, pay for) opinions issued by CRAs to help them raise capital. Investors and lenders typically insist on being compensated for uncertainty and, when taking on debt, issuers pay for this uncertainty through higher interest rates.2 CRA opinions that help reduce uncertainty for investors also help reduce the cost of capital for issuers. Lenders and investors in fixed- income securities, by contrast, use CRA ratings in assessing the likely risks they face when lending money to or investing in the securities of a particular issuer. Institutional investors and fiduciary investors (i.e., those with independent authority to invest on behalf of others, such as the managers of trust funds or pensions), likewise, use CRA ratings to help them allocate investments in a diversified risk portfolio. -

Municipal Finance in Sweden
FACTSHEET April 2021 Municipal Finance in Sweden Fedra Vanhuyse, Stockholm Environment Institute Astrid Nilsson, Stockholm Environment Institute Venni Arra, Stockholm Environment Institute Alicia Requena, Cleantech Scandinavia Magnus Agerström, Cleantech Scandinavia For most Swedish citizens, their closest engagement with the Funding of Swedish municipalities government happens through the municipalities they live in. In Sweden, there are 290 municipalities that are responsible In Sweden, a municipality’s revenue mostly comes from taxes, for providing its inhabitants with numerous services, including fees for certain services and government grants. Municipal tax is education and childcare, non-medical health care, social care, the main source of revenue. For all residents in Sweden to have waste and water treatment, and environmental management. access to equal services, regardless of where they live, there is a tax equalization system, in which differences in tax revenues and This factsheet offers some introductory insights into how expenditure needs are balanced so that all municipalities have municipal governments are financed and what their budgets approximately the same tax base, I.e., revenue per inhabitant. entail. It draws upon research carried out by the Viable Cities’ It works in two ways: 1) on the revenue side, it evens out the Finance project. This project assesses how cities can fund differences in tax base per capita and 2) on the expenditures side, their investments in sustainability. We provide examples of it distributes funds and grants to local governments with adverse nine Swedish municipalities: Gothenburg, Linköping, Lund, cost structures and unfavourable demographic compositions. Malmö, Nacka, Örebro, Östersund, Västerås and Vellinge. Other income sources include financial results such as interest These cities were selected as they have issued a green bond, rates on funds in the bank and on loans. -

Kingdom of the Netherlands Rating Report
30 June 2017 Public Finance Kingdom of the Netherlands KingdomRating of theReport Netherlands STABLE Rating Report AAA OUTLOOK Credit strengths Credit weaknesses Ratings & Outlook Wealthy & diversified economy High household debt Foreign currency Strong current account balance Susceptibility to external shocks Long-term issuer rating AAA/Stable Senior unsecured debt AAA/Stable Robust fiscal position Labour market inefficiencies Short-term issuer rating S-1+/Stable Rating rationale and Outlook: The AAA rating is supported by a wealthy, flexible and Local currency export-oriented economy, which performed strongly in 2016 following the double-dip recession. The Netherlands benefits from strong external position, prudent fiscal policy, LongL -term issuer rating AAA/Stable o moderate public debt underpinned by resilient GDP growth, and well-established fiscal Senior unsecured debt AAA/Stable framework. At the same time, high private-sector debt, susceptibility to external risks and c Short-term issuer rating S-1+/Stable labour market inefficiencies pose some concerns. The Stable Outlook reflects Scope’s a expectation of a continuation of the government’s prudent fiscal policy, with public debt l declining over the medium term. C Figure 1: Summary of sovereign rating categories u rLead Analyst rDr Ilona Dmitrieva e+44 6966773-13 n [email protected] c Team Leader y Dr Giacomo Barisone +49 69 6677389-22 [email protected] Scope Ratings AG Neue Mainzer Straße 66-68 60311 Frankfurt am Main Phone + 49 69 6677389 0 Headquarters -

Exploratory Study on the Use of Credit Ratings in the Netherlands
Exploratory study on the use of credit ratings in the Netherlands The Netherlands Authority for the Financial Markets The AFM promotes fairness and transparency within financial markets. We are the independent supervisory authority for the savings, lending, investment and insurance markets. The AFM promotes the conscientious provision of financial services to consumers and supervises the honest and efficient operation of the capital markets. Our aim is to improve consumers' and the business sector's confidence in the financial markets, both in the Netherlands and abroad. In performing this task the AFM contributes to the prosperity and economic reputation of the Netherlands. 2 Table of contents Preface 4 1 Study outline 5 2 Ratings to determine counterparties 7 3 Ratings as a tool for investment limits 9 4 Decision making based on ratings 11 5 Other use of ratings 14 6 New legislation relevant for users of ratings 17 7 Conclusion 18 Annex 1: Preliminary overview of the users of ratings and the purpose why ratings are used 19 Annex 2: Charts from the AFM study towards the behaviour of consumers/retail investors 20 Annex 3: Charts from the AFM study towards the behaviour of investor firms and collective investment schemes 21 3 Preface Since the credit crisis started in 2007, credit rating agencies (CRAs) are criticised for their performance. They were accused of rating structured finance instruments, such as asset backed securities, inaccurately. When the underlying assets eventually turned out less creditworthy, it led to large downgrades. The question rose if the CRAs were biased in their rating due to potential conflicts of interest such as pressure from issuers or due to lack of competition. -

Country Risk Service Handbook
Country Risk Service Handbook The world leader in global business intelligence The Economist Intelligence Unit (The EIU) is the research and analysis division of The Economist Group, the sister company to The Economist newspaper. Created in 1946, we have over 70 years’ experience in helping businesses, financial firms and governments to understand how the world is changing and how that creates opportunities to be seized and risks to be managed. Given that many of the issues facing the world have an international (if not global) dimension, The EIU is ideally positioned to be commentator, interpreter and forecaster on the phenomenon of globalisation as it gathers pace and impact. EIU subscription services The world’s leading organisations rely on our subscription services for data, analysis and forecasts to keep them informed about what is happening around the world. We specialise in: • Country Analysis: Access to regular, detailed country-specific economic and political forecasts, as well as assessments of the business and regulatory environments in different markets. • Risk Analysis: Our risk services identify actual and potential threats around the world and help our clients understand the implications for their organisations. • Industry Analysis: Five year forecasts, analysis of key themes and news analysis for six key industries in 60 major economies. These forecasts are based on the latest data and in-depth analysis of industry trends. EIU Consulting EIU Consulting is a bespoke service designed to provide solutions specific to our customers’ needs. We specialise in these key sectors: • Healthcare: Together with our two specialised consultancies, Bazian and Clearstate, The EIU helps healthcare organisations build and maintain successful and sustainable businesses across the healthcare ecosystem. -

Swedish Export Credit Corp
Swedish Export Credit Corp. Primary Credit Analyst: Pierre-Brice Hellsing, Stockholm + 46 84 40 5906; [email protected] Secondary Contact: Erik Andersson, Stockholm + 46 84 40 5915; [email protected] Table Of Contents Major Rating Factors Outlook Rationale Related Criteria Related Research WWW.STANDARDANDPOORS.COM/RATINGSDIRECT DECEMBER 6, 2019 1 Swedish Export Credit Corp. Additional SACP a- Support +5 0 + + Factors Anchor a- Issuer Credit Rating ALAC 0 Business Support Moderate Position -1 Capital and GRE Support Very Strong +5 Earnings +2 Risk Position Moderate -1 Group AA+/Stable/A-1+ Support 0 Funding Average 0 Sovereign Liquidity Adequate Support 0 Major Rating Factors Strengths: Weaknesses: • Extremely high likelihood of government support. • Heavy reliance on foreign wholesale funding, • Strong loan asset quality and high-quality including structured funding. guarantees. • Concentration on large individual loan exposures. • Robust capitalization well above international • Relatively low profitability. average. WWW.STANDARDANDPOORS.COM/RATINGSDIRECT DECEMBER 6, 2019 2 Swedish Export Credit Corp. Outlook: Stable The stable outlook on Swedish Export Credit Corp. (SEK) reflects S&P Global Ratings' view that there is an extremely high likelihood of timely support to SEK from the Swedish government, if needed, over the next two years. The outlook also reflects our expectation that the company's asset quality will remain strong and its liquidity and capitalization robust. Given the level of extraordinary support and our 'AAA' rating on Sweden, we could revise our assessment of SEK's stand-alone credit profile (SACP) downward by four notches without it affecting the rating. While presently unlikely, we could consider a negative rating action if we saw that SEK's role or link with the Swedish government were weakening. -

The National Credit Bureau: a Key Enabler of Financial Infrastructure and Lending in Developing Economies
Risk Practice McKINSEY WORKING PAPERS ON RISK The national credit bureau: A key enabler of financial infrastructure and lending in developing economies Number 14 Tobias Baer, December 2009 Massimo Carassinu, Andrea Del Miglio, Claudio Fabiani, and Edoardo Ginevra Confidential Working Paper. No part may be circulated, quoted, or reproduced for distribution without prior written approval from McKinsey & Company. The national credit bureau: a key enabler of financial infrastructure and lending in developing economies Contents Introduction 2 Lending in emerging markets: a vexed terrain 3 The credit bureau as key enabler of emerging markets lending 4 Credit bureaus in developing and emerging economies 7 Setting up a national credit bureau: addressing the key issues 8 Key lessons from real credit bureau implementations in developing countries 15 McKinsey Working Papers on Risk presents McKinsey's best current thinking on risk and risk management. The constituent papers represent a broad range of views, both sector-specific and cross-cutting, and are intended to encourage discussion internally and externally. Working papers may be republished through other internal or external channels. Please address correspondence to the managing editor, Rob McNish, [email protected] 2 Introduction The challenges of lending in developing economies are unique. Across most of Africa and in some countries in Asia and Latin America the credit bureau can be a key enabler for expanding lending business, because it distributes information about the payment behavior of consumers and commercial entities. Credit bureaus Increase access to credit Support responsible lending and reduce credit losses Strengthen banking supervision in monitoring systemic risks. Despite the advantages of a national credit bureau, many developing countries either do not have them at all or have low-performing bureaus with extremely limited service coverage.