DOCSLIB.ORG

AAE 637 Lab 3: Hypothesis Testing⇤

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
AAE 637 Lab 3: Hypothesis Testing⇤ AAE 637 Lab 3: Hypothesis testing⇤ 2/11/2015 The Wald test You are familiar with the t-test. Usually the null hypothesis is that β =0. If the null is β = β0: βˆ β0 tn (β0)= − s βˆ ⇣ ⌘ where s βˆ the standard error (i.e. the square root of the variance) of the estimate. For a two-sided test⇣ ⌘ we reject the null hypothesis at the 5% confidence level if tn 1.96. | |≥ The Wald test is a generalization of the t-test so we can conduct tests dealing with multiple parameters and/or multiple restrictions. Let’s square the t-stat: 2 βˆ β0 2 − (tn (β0)) = ⇣ s2 βˆ ⌘ ⇣ ⌘ 2 βˆ β is assumed to be normally distributed, so βˆ β is distributed χ2 (“chi-squared”), − 0 − 0 2 with 1 degree of freedom. With Fq (u) denoting the ⇣χq density⌘ function, the critical value v for rejection of the null hypothesis at significance level ↵ satisfies ↵ =1 F (v).For↵ =0.05 and − q q =1,thiscriticalvalueis3.84,i.e.werejectthenullif(t (β ))2 3.84. n 0 ≥ 2 χ1 distribution 1.2 95% of mass 5% of mass 0.8 Density 0.4 0.0 0 2 4 6 8 10 Value of Wald statistic ⇤prepared by Travis McArthur, UW-Madison (http://www.aae.wisc.edu/tdmcarthur/teaching.asp) 1 For the Wald statistic, we can express any set of q linear restrictions on K parameter values with matrix notation: R β = c q KK 1 q 1 ⇥ ⇥ ⇥ Say we have four parameters and we wish to test the joint hypothesis that β + β β =1and 1 2 − 3 β1 = 10. Let’s make the first row of R: β + β β = β 1+β 1+β ( 1) + β 0 1 2 − 3 1 · 2 · 3 · − 4 · and the second row: β = β 1+β 0+β 0+β 0 1 1 · 2 · 3 · 4 · 11 10 1 So R = , c = 10− 0 0 10 The Wald statistic is given by: 0 1 − 0 Wn = R βˆ c R Vˆ R R βˆ c q KK 1 − q 1 q KK KK q q KK 1 − q 1 ⇥ ⇥ ⇥ ✓ ⇥ ⇥ ⇥ ◆ ⇥ ⇥ ⇥ W χ2 n ⇠ q Vˆ is the estimated asymptotic variance-covariance matrix of the parameters βˆ.Youmustuse the correct number of degrees of freedom on χ2 to do the Wald test and/or compute the p-value. The degrees of freedom here are the number of restrictions (i.e. rows of R), not the number of parameters being tested. The key thing here is that the covariance across the parameter estimates must be taken into account when you compare parameter estimates within the same model and/or dataset. To get the p-value in MATLAB, input something like: 1-chi2cdf(w_test_output,size(R_mat,1)) The F test The F statistic can be used to test multiple hypotheses as well, but it is extremely similar to the Wald stat. In fact, when the homoskedastic estimate of V is used in the Wald stat, we have: W F = n n q However, the F statistic is compared against the F distribution, which incorporates a “small sample” correction. F F [q, n K] where K is the number of estimated parameters and n is the n ⇠ − number of observations. As n ,theF distribution converges to a χ2 distribution if multiplied !1 q by q. The F statistic can also be expressed in terms of the sum of squared errors of an OLS regression: SSE β˜ SSE βˆ /q cls − Fn = ⇣ SSE⇣ βˆ⌘ / (n ⇣K)⌘⌘ − ⇣ ⌘ ˜ Where SSE βcls is the sum of squared errors for the constrained model. The F test is often ⇣ ⌘ ˜ used to check whether a model has any explanatory power at all, in which case SSE βcls would be the total sum of squares. This type of F test was more relevant in the past when⇣ only⌘ small datasets were available. 2 The delta method Say we know that the asymptotic distribution of a K 1 consistent set of estimators βˆ is jointly ⇥ normal, i.e. as n , !1 pn βˆ β d N 0 , V K 1 − K 1 ! K 1 K K ✓ ⇥ ⇥ ◆ ✓ ⇥ ⇥ ◆ Further suppose that what we really want to get out of our estimation is some continuously differentiable transformation g : RK RL of our parameter estimates, not the estimates them- ! selves. In addition to obtaining the transformed estimates, we need to know the uncertainty of the transformed estimates. The delta method gives us the following asymptotic approximation of the variance of the transformed estimates: 0 ˆ d @ @ pn g β g (β) N 0 , @β g (β) V @β g (β) 0 − L 1 1 ! 0L 1 K K 1 L 1 ⇥ ⇥ L K ⇥ K L ⇣⇥ ⌘ h ⇥ i h ⇥ i @ @ A @ A where @β g (β) is the Jacobian matrix: @ @ g1 (β) g1 (β) @1 ··· @K @ . @β g (β)=2 . .. 3 @ @ gL (β) gL (β) 6 @1 ··· @K 7 4 5 The delta method works because it is a first-order Taylor Series approximation of the true variance. Now say we can consistently estimate V. Then our estimator for the variance of g βˆ is simply the “plug-in” estimator: ⇣ ⌘ 0 @ ˆ ˆ @ ˆ @β g β V @β g β h ⇣ ⌘i h ⇣ ⌘i Example: ˆ ˆ 0.5 1 0.5 β1/β2 Say βˆ = , Vˆ = − , g βˆ = 2 1.5 0.52 βˆ − " 2 # 2 ⇣ ⌘ ˆ ˆ ˆ ⇣ ⌘ @ ˆ 1/β2 β1/ β2 Then: @β g β = − " 02βˆ⇣ ⌘ # ⇣ ⌘ 2 This implies that the variance-covariance estimate for g βˆ is: ⇣ ⌘ 0 1/1.5 0.5/ (1.5)2 1 0.5 1/1.5 0.5/ (1.5)2 0.691 2.3¯ Vˆ = − = − g(β) 02− 1.5 0.52 02− 1.5 2.3¯ 18 · − · − 1 Now say my null hypothesis is g (β)= 2 Then the Wald stat is: 0 1/3 1 ˆ 1 1/3 1 Wn = V− t 1.038 2.25 − 2 g(β) 2.25 − 2 ✓ ◆ ✓ ◆ 2 Using the χ2 distribution, this yields a p-value of 0.60, so we cannot reject the null hypothesis. When the parameter restrictions being tested are nonlinear, different algebraic formulations of the restriction can affect the value of the Wald statistic. This is undesirable. Next lab we will discuss likelihood-based tests that do not suffer from this problem. 3.
Load more

Recommended publications
  • Chapter 8 Large Sample Theory
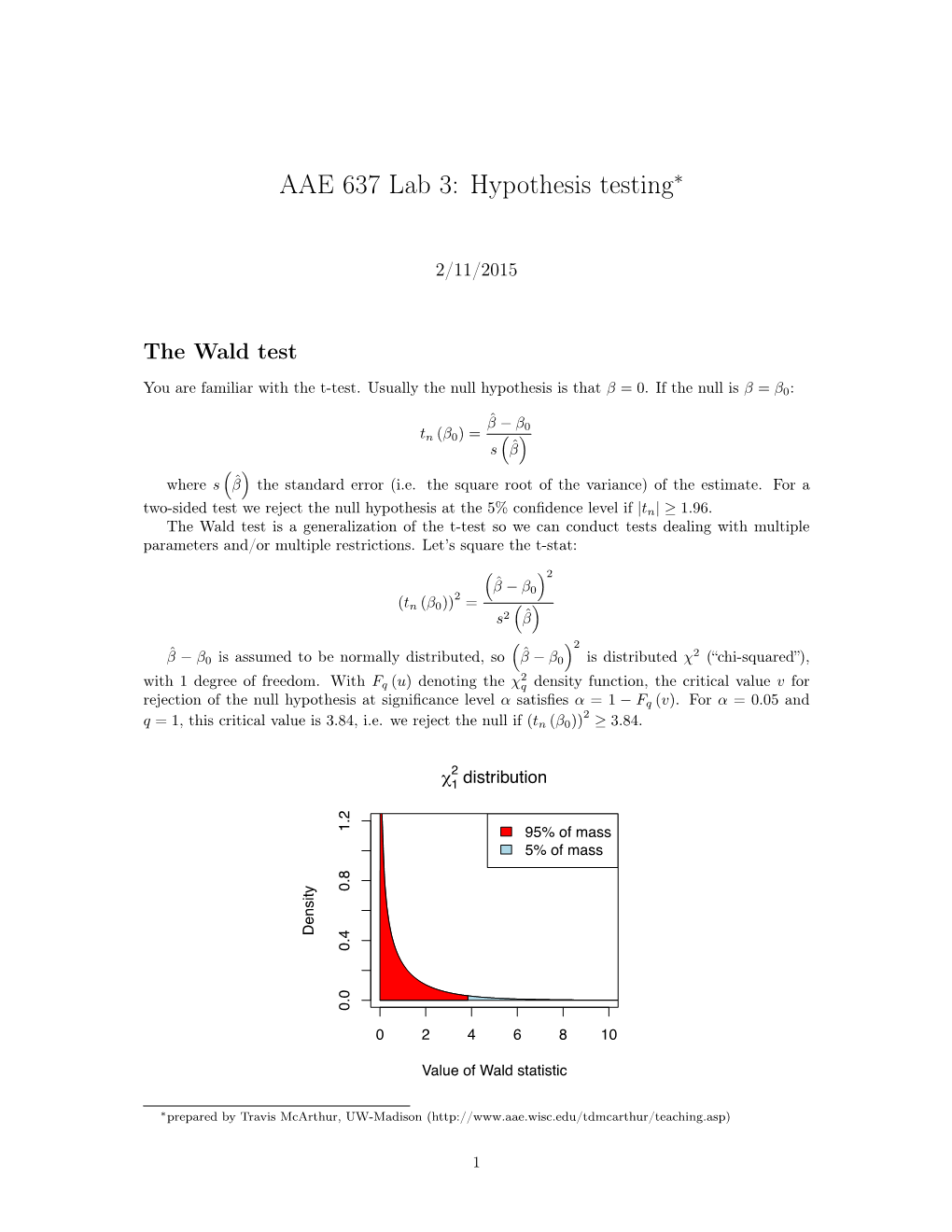
    Chapter 8 Large Sample Theory 8.1 The CLT, Delta Method and an Expo- nential Family Limit Theorem Large sample theory, also called asymptotic theory, is used to approximate the distribution of an estimator when the sample size n is large. This theory is extremely useful if the exact sampling distribution of the estimator is complicated or unknown. To use this theory, one must determine what the estimator is estimating, the rate of convergence, the asymptotic distribution, and how large n must be for the approximation to be useful. Moreover, the (asymptotic) standard error (SE), an estimator of the asymptotic standard deviation, must be computable if the estimator is to be useful for inference. Theorem 8.1: the Central Limit Theorem (CLT). Let Y1,...,Yn be 2 1 n iid with E(Y )= µ and VAR(Y )= σ . Let the sample mean Y n = n i=1 Yi. Then √n(Y µ) D N(0,σ2). P n − → Hence n Y µ Yi nµ D √n n − = √n i=1 − N(0, 1). σ nσ → P Note that the sample mean is estimating the population mean µ with a √n convergence rate, the asymptotic distribution is normal, and the SE = S/√n where S is the sample standard deviation. For many distributions 203 the central limit theorem provides a good approximation if the sample size n> 30. A special case of the CLT is proven at the end of Section 4. Notation. The notation X Y and X =D Y both mean that the random variables X and Y have the same∼ distribution.
    [Show full text]
  • Applying the Delta Method in Metric Analytics
    Applying the Delta Method in Metric Analytics: A Practical Guide with Novel Ideas Alex Deng Ulf Knoblich Jiannan Lu∗ Microsoft Corporation Microsoft Corporation Microsoft Corporation Redmond, WA Redmond, WA Redmond, WA [email protected] [email protected] [email protected] ABSTRACT variance of a normal distribution from independent and identically During the last decade, the information technology industry has distributed (i.i.d.) observations, we only need to obtain their sum adopted a data-driven culture, relying on online metrics to measure and sum of squares, which are the corresponding summary statis- 1 and monitor business performance. Under the setting of big data, tics and can be trivially computed in a distributed fashion. In data- the majority of such metrics approximately follow normal distribu- driven businesses such as information technology, these summary tions, opening up potential opportunities to model them directly statistics are often referred to as metrics, and used for measuring without extra model assumptions and solve big data problems via and monitoring key performance indicators [15, 18]. In practice, it closed-form formulas using distributed algorithms at a fraction of is often the changes or differences between metrics, rather than the cost of simulation-based procedures like bootstrap. However, measurements at the most granular level, that are of greater inter- certain attributes of the metrics, such as their corresponding data est. In the context of randomized controlled experimentation (or generating processes and aggregation levels, pose numerous chal- A/B testing), inferring the changes of metrics can establish causal- lenges for constructing trustworthy estimation and inference pro- ity [36, 44, 50], e.g., whether a new user interface design causes cedures.
    [Show full text]
  • Chapter 6 Asymptotic Distribution Theory
    RS – Chapter 6 Chapter 6 Asymptotic Distribution Theory Asymptotic Distribution Theory • Asymptotic distribution theory studies the hypothetical distribution -the limiting distribution- of a sequence of distributions. • Do not confuse with asymptotic theory (or large sample theory), which studies the properties of asymptotic expansions. • Definition Asymptotic expansion An asymptotic expansion (asymptotic series or Poincaré expansion) is a formal series of functions, which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular, often infinite, point. (In asymptotic distribution theory, we do use asymptotic expansions.) 1 RS – Chapter 6 Asymptotic Distribution Theory • In Chapter 5, we derive exact distributions of several sample statistics based on a random sample of observations. • In many situations an exact statistical result is difficult to get. In these situations, we rely on approximate results that are based on what we know about the behavior of certain statistics in large samples. • Example from basic statistics: What can we say about 1/ x ? We know a lot about x . What do we know about its reciprocal? Maybe we can get an approximate distribution of 1/ x when n is large. Convergence • Convergence of a non-random sequence. Suppose we have a sequence of constants, indexed by n f(n) = ((n(n+1)+3)/(2n + 3n2 + 5) n=1, 2, 3, ..... 2 Ordinary limit: limn→∞ ((n(n+1)+3)/(2n + 3n + 5) = 1/3 There is nothing stochastic about the limit above. The limit will always be 1/3. • In econometrics, we are interested in the behavior of sequences of real-valued random scalars or vectors.
    [Show full text]
  • The 'Delta Method'
    B Appendix The ‘Delta method’ ... Suppose you have done a study, over 4 years, which yields 3 estimates of survival (say, φ1, φ2, and φ3). But, suppose what you are really interested in is the estimate of the product of the three survival values (i.e., the probability of surviving from the beginning of the study to the end of theb study)?b Whileb it is easy enough to derive an estimate of this product (as [φ φ φ ]), how do you derive 1 × 2 × 3 an estimate of the variance of the product? In other words, how do you derive an estimate of the variance of a transformation of one or more random variables (inb thisb case,b we transform the three random variables - φi - by considering their product)? One commonly used approach which is easily implemented, not computer-intensive, and can be robustly applied inb many (but not all) situations is the so-called Delta method (also known as the method of propagation of errors). In this appendix, we briefly introduce the underlying background theory, and the implementation of the Delta method, to fairly typical scenarios. B.1. Mean and variance of random variables Our primary interest here is developing a method that will allow us to estimate the mean and variance for functions of random variables. Let’s start by considering the formal approach for deriving these values explicitly, based on the method of moments. For continuous random variables, consider a continuous function f (x) on the interval [ ∞, +∞]. The first three moments of f (x) can be written − as +∞ M0 = f (x)dx ∞ Z− +∞ M1 = x f (x)dx ∞ Z− +∞ 2 M2 = x f (x)dx ∞ Z− In the particular case that the function is a probability density (as for a continuous random variable), then M0 = 1 (i.e., the area under the PDF must equal 1).
    [Show full text]
  • Chapter 5 the Delta Method and Applications
    Chapter 5 The Delta Method and Applications 5.1 Linear approximations of functions In the simplest form of the central limit theorem, Theorem 4.18, we consider a sequence X1,X2,... of independent and identically distributed (univariate) random variables with finite variance σ2. In this case, the central limit theorem states that √ d n(Xn − µ) → σZ, (5.1) where µ = E X1 and Z is a standard normal random variable. In this chapter, we wish to consider the asymptotic distribution of, say, some function of Xn. In the simplest case, the answer depends on results already known: Consider a linear function g(t) = at+b for some known constants a and b. Since E Xn = µ, clearly E g(Xn) = aµ + b =√g(µ) by the linearity of the expectation operator. Therefore, it is reasonable to ask whether n[g(Xn) − g(µ)] tends to some distribution as n → ∞. But the linearity of g(t) allows one to write √ √ n g(Xn) − g(µ) = a n Xn − µ . We conclude by Theorem 2.24 that √ d n g(Xn) − g(µ) → aσZ. Of course, the distribution on the right hand side above is N(0, a2σ2). None of the preceding development is especially deep; one might even say that it is obvious that a linear transformation of the random variable Xn alters its asymptotic distribution 85 by a constant multiple. Yet what if the function g(t) is nonlinear? It is in this nonlinear case that a strong understanding of the argument above, as simple as it may be, pays real dividends.
    [Show full text]
  • Stat 8931 (Aster Models) Lecture Slides Deck 4 [1Ex] Large Sample
    Stat 8931 (Aster Models) Lecture Slides Deck 4 Large Sample Theory and Estimating Population Growth Rate Charles J. Geyer School of Statistics University of Minnesota October 8, 2018 R and License The version of R used to make these slides is 3.5.1. The version of R package aster used to make these slides is 1.0.2. This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License (http://creativecommons.org/licenses/by-sa/4.0/). The Delta Method The delta method is a method (duh!) of deriving the approximate distribution of a nonlinear function of an estimator from the approximate distribution of the estimator itself. What it does is linearize the nonlinear function. If g is a nonlinear, differentiable vector-to-vector function, the best linear approximation, which is the Taylor series up through linear terms, is g(y) − g(x) ≈ rg(x)(y − x); where rg(x) is the matrix of partial derivatives, sometimes called the Jacobian matrix. If gi (x) denotes the i-th component of the vector g(x), then the (i; j)-th component of the Jacobian matrix is @gi (x)=@xj . The Delta Method (cont.) The delta method is particularly useful when θ^ is an estimator and θ is the unknown true (vector) parameter value it estimates, and the delta method says g(θ^) − g(θ) ≈ rg(θ)(θ^ − θ) It is not necessary that θ and g(θ) be vectors of the same dimension. Hence it is not necessary that rg(θ) be a square matrix. The Delta Method (cont.) The delta method gives good or bad approximations depending on whether the spread of the distribution of θ^ − θ is small or large compared to the nonlinearity of the function g in the neighborhood of θ.
    [Show full text]
  • Taylor Approximation and the Delta Method
    Taylor Approximation and the Delta Method Alex Papanicolaou∗ April 28, 2009 1 Taylor Approximation 1.1 Motivating Example: Estimating the odds Suppose we observe X1;:::;Xn independent Bernoulli(p) random variables. Typically, we are p interested in p but there is also interest in the parameter 1−p , which is known as the odds. For example, if the outcomes of a medical treatment occur with p = 2=3, then the odds of getting better is 2 : 1. Furthermore, if there is another treatment with success probability r, we might also be p r interested in the odds ratio 1−p = 1−r , which gives the relative odds of one treatment over another. If we wished to estimate p, we would typically estimate this quantity with the observed success P p^ probabilityp ^ = i Xi=n. To estimate the odds, it then seems perfectly natural to use 1−p^ as an p estimate for 1−p . But whereas we know the variance of our estimatorp ^ is p(1 − p) (check this p^ be computing var(^p)), what is the variance of 1−p^? Or, how can we approximate its sampling distribution? The Delta Method gives a technique for doing this and is based on using a Taylor series approxi- mation. 1.2 The Taylor Series (r) dr Definition: If a function g(x) has derivatives of order r, that is g (x) = dxr g(x) exists, then for any constant a, the Taylor polynomial of order r about a is r X g(k)(a) T (x) = (x − a)k: r k! k=0 While the Taylor polynomial was introduced as far back as beginning calculus, the major theorem from Taylor is that the remainder from the approximation, namely g(x) − Tr(x), tends to 0 faster than the highest-order term in Tr(x).
    [Show full text]
  • TESTING for the PARETO DISTRIBUTION Suppose That X1
    1 M3S3/M4S3 STATISTICAL THEORY II WORKED EXAMPLE: TESTING FOR THE PARETO DISTRIBUTION Suppose that X1;:::;Xn are i.i.d random variables having a Pareto distribution with pdf θcθ f (xjθ) = x > c Xjθ xθ+1 and zero otherwise, for known constant c > 0, and parameter θ > 0. (i) Find the ML estimator, θbn, of θ, and ¯nd the asymptotic distribution of p n(θbn ¡ θT ) where θT is the true value of θ. (ii) Consider testing the hypotheses of H0 : θ = θ0 H1 : θ 6= θ0 for some θ0 > 0. Determine the likelihood ratio, Wald and Rao tests of this hypothesis. SOLUTION (i) The ML estimate θbn is computed in the usual way: Yn Yn θcθ θncnθ Ln(θ) = fXjθ(xijθ) = θ+1 = θ+1 i=1 i=1 xi sn Yn where sn = xi. Then i=1 ln(θ) = n log θ + nθ log c ¡ (θ + 1) log sn n l_ (θ) = + n log c ¡ log s n θ n and solving l_n(θ) = 0 yields the ML estimate · ¸ " #¡1 log s ¡1 1 Xn θb = n ¡ log c = log x ¡ log c : n n n i i=1 The corresponding estimator is therefore " #¡1 1 Xn θb = log X ¡ log c : n n i i=1 Computing the asymptotic distribution directly is di±cult because of the reciprocal. However, consider Á = 1/θ; by invariance, the ML estimator of Á is 1 Xn 1 Xn Áb = log X ¡ log c = (log X ¡ log c) n n i n i i=1 i=1 2 which implies how we should compute the asymptotic distribution of θbn - we use the CLT on the random variables Yi = log Xi ¡ log c = log(Xi=c), and then use the Delta Method.
    [Show full text]
  • Uniformity and the Delta Method
    Uniformity and the delta method Maximilian Kasy∗ January 1, 2018 Abstract When are asymptotic approximations using the delta-method uniformly valid? We provide sufficient conditions as well as closely related necessary conditions for uniform neg- ligibility of the remainder of such approximations. These conditions are easily verified by empirical practitioners and permit to identify settings and parameter regions where point- wise asymptotic approximations perform poorly. Our framework allows for a unified and transparent discussion of uniformity issues in various sub-fields of statistics and economet- rics. Our conditions involve uniform bounds on the remainder of a first-order approximation for the function of interest. ∗Associate professor, Department of Economics, Harvard University. Address: Littauer Center 200, 1805 Cambridge Street, Cambridge, MA 02138. email: [email protected]. 1 1 Introduction Many statistical and econometric procedures are motivated and justified using asymptotic ap- proximations.1 Standard asymptotic theory provides approximations for fixed parameter values, letting the sample size go to infinity. Procedures for estimation, testing, or the construction of confidence sets are considered justified if they perform well for large sample sizes, for any given parameter value. Procedures that are justified in this sense might unfortunately still perform poorly for arbi- trarily large samples. This happens if the asymptotic approximations invoked are not uniformly valid. In that case there are parameter values for every sample size such that the approximation is poor, even though for every given parameter value the approximation performs well for large enough sample sizes. Which parameter values cause poor behavior might depend on sample size, so that poor behavior does not show up in standard asymptotics.
    [Show full text]
  • Calculating Confidence Intervals for Continuous and Discontinuous Functions of Estimated Parameters
    IZA DP No. 5816 Calculating Confi dence Intervals for Continuous and Discontinuous Functions of Estimated Parameters John Ham Tiemen Woutersen June 2011 DISCUSSION PAPER SERIES Forschungsinstitut zur Zukunft der Arbeit Institute for the Study of Labor Calculating Confidence Intervals for Continuous and Discontinuous Functions of Estimated Parameters John Ham University of Maryland, IRP (Madison), IFAU and IZA Tiemen Woutersen Johns Hopkins University Discussion Paper No. 5816 June 2011 IZA P.O. Box 7240 53072 Bonn Germany Phone: +49-228-3894-0 Fax: +49-228-3894-180 E-mail: [email protected] Any opinions expressed here are those of the author(s) and not those of IZA. Research published in this series may include views on policy, but the institute itself takes no institutional policy positions. The Institute for the Study of Labor (IZA) in Bonn is a local and virtual international research center and a place of communication between science, politics and business. IZA is an independent nonprofit organization supported by Deutsche Post Foundation. The center is associated with the University of Bonn and offers a stimulating research environment through its international network, workshops and conferences, data service, project support, research visits and doctoral program. IZA engages in (i) original and internationally competitive research in all fields of labor economics, (ii) development of policy concepts, and (iii) dissemination of research results and concepts to the interested public. IZA Discussion Papers often represent preliminary work and are circulated to encourage discussion. Citation of such a paper should account for its provisional character. A revised version may be available directly from the author.
    [Show full text]
  • MLE Lecture 4.Pdf
    Lecture 4 Estimating the Asymptotic Covariance Matrices of Maximum Likelihood Estimators The asymptotic variance-covariance matrix of MLEs can be estimated by −1 2 −1 ∂ ln L [I (θ )] = − E . ~ |θ =θˆ ∂θ ∂θ′ ~ ~ ML ~ ~ |θ =θˆ ~ ~ ML However, this estimator may not be available because of the difficulty in calculating the necessary expectations to get the information matrix. There do, however, exist two alternative consistent estimators. Alternative 1 (Direct use of Hessian) −1 2 −1 −1 ∂ ln L(θ ) [Iˆ(θˆ)] = [− H (θˆ)] = − ~ ~ ~ ∂θ ∂θ′ ~ ~ |θ =θˆ ~ ~ where plimθˆ = θ . ~ ~ Of course, θˆ could be chosen as the maximum likelihood estimator θˆ . ~ ~ ML Alternative 2 (BHHH or outer product of gradients) − −1 N 1 ˆ ˆ ˆ ˆ −1 I (θ ) = gˆi gˆi′ = [GG′] ~ ∑ i=1 ~ ~ ∂ln L X i ;θ ~ ˆ = ˆ ˆ ˆ ˆ = ~ where G g1 g2 gN and gi ~ ~ ~ ~ ∂θ ~ |θ =θ ~ ~ ML The first alternative requires the derivation of the second derivations of the log likelihood function (i.e., the Hessian matrix) while the second alternative only requires 1 the derivation of the first derivatives of the log likelihood function (i.e., the gradient vector). Alternative 3 (QMLE/Sandwich Variance-Covariance Matrix) For the Type 2 ML estimator (see Davidson and McKinnon (2004, p. 406)) it can be shown that 1/ 2 ˆ −1 −1 Var( p lim n (θ −θ 0 )) = H (θ 0 ) I(θ 0 )H (θ 0 ) . n→∞ ~ ~ ~ ~ ~ Therefore, a consistent estimate of the variance-covariance matrix of the Type 2 ML estimator is ˆ ˆ −1 ˆ ˆ ˆ −1 VaˆrQMLE (θ ) = [H (θ )] GG'[H (θ )] .
    [Show full text]
  • Large Sample Tools∗ STA 312: Fall 2012
    Large Sample Tools∗ STA 312: Fall 2012 Background Reading: Davison's Statistical models • For completeness, look at Section 2.1, which presents some basic applied statistics in an advanced way. • Especially see Section 2.2 (Pages 28-37) on convergence. • Section 3.3 (Pages 77-90) goes more deeply into simulation than we will. At least skim it. Overview Contents 1 Foundations2 2 Law of Large Numbers3 3 Consistency7 4 Central Limit Theorem8 5 Convergence of random vectors 10 6 Delta Method 11 ∗See last slide for copyright information. 1 1 Foundations Sample Space Ω, ! 2 Ω • Observe whether a single individual is male or female: Ω = fF; Mg • Pair of individuals; observe their genders in order: Ω = f(F; F ); (F; M); (M; F ); (M; M)g • Select n people and count the number of females: Ω = f0; : : : ; ng For limits problems, the points in Ω are infinite sequences. Random variables are functions from Ω into the set of real numbers P rfX 2 Bg = P r(f! 2 Ω: X(!) 2 Bg) Random Sample X1(!);:::;Xn(!) • T = T (X1;:::;Xn) • T = Tn(!) • Let n ! 1 to see what happens for large samples Modes of Convergence • Almost Sure Convergence • Convergence in Probability • Convergence in Distribution Almost Sure Convergence a:s: We say that Tn converges almost surely to T , and write Tn ! if P rf! : lim Tn(!) = T (!)g = 1: n!1 • Acts like an ordinary limit, except possibly on a set of probability zero. • All the usual rules apply. • Called convergence with probability one or sometimes strong convergence.
    [Show full text]