DOCSLIB.ORG

The Project Gutenberg Ebook #26839: Mathematical Recreations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Project Gutenberg Ebook #26839: Mathematical Recreations Project Gutenberg’s Mathematical Recreations and Essays, by W. W. Rouse Ball This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Mathematical Recreations and Essays Author: W. W. Rouse Ball Release Date: October 8, 2008 [EBook #26839] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK MATHEMATICAL RECREATIONS *** First Edition, Feb. 1892. Reprinted, May, 1892. Second Edition, 1896. Reprinted, 1905. MATHEMATICAL RECREATIONS AND ESSAYS BY W.W. ROUSE BALL Fellow and Tutor of Trinity College, Cambridge. FOURTH EDITION MACMILLAN AND CO., Limited NEW YORK: THE MACMILLAN COMPANY 1905 [All rights reserved.] Produced by Joshua Hutchinson, David Starner, David Wilson and the Online Distributed Proofreading Team at http://www.pgdp.net Transcriber's notes Most of the open questions discussed by the author were settled during the twentieth century. The author's footnotes are labelled using printer's marks*; footnotes showing where corrections to the text have been made are labelled numerically1. Minor typographical corrections are documented in the LATEX source. This document is designed for two-sided printing. Consequently, the many hyperlinked cross-references are not visually distinguished. The document can be recompiled for more comfortable on-screen viewing: see comments in source LATEX code. PREFACE TO THE FIRST EDITION. The following pages contain an account of certain mathematical recreations, problems, and speculations of past and present times. I hasten to add that the conclusions are of no practical use, and most of the results are not new. If therefore the reader proceeds further he is at least forewarned. At the same time I think I may assert that many of the diversions| particularly those in the latter half of the book|are interesting, not a few are associated with the names of distinguished mathematicians, while hitherto several of the memoirs quoted have not been easily ac- cessible to English readers. The book is divided into two parts, but in both parts I have in- cluded questions which involve advanced mathematics. The first part consists of seven chapters, in which are included var- ious problems and amusements of the kind usually called mathematical recreations. The questions discussed in the first of these chapters are connected with arithmetic; those in the second with geometry; and those in the third relate to mechanics. The fourth chapter contains an account of some miscellaneous problems which involve both num- ber and situation; the fifth chapter contains a concise account of magic squares; and the sixth and seventh chapters deal with some unicursal iii iv PREFACE problems. Several of the questions mentioned in the first three chap- ters are of a somewhat trivial character, and had they been treated in any standard English work to which I could have referred the reader, I should have pointed them out. In the absence of such a work, I thought it best to insert them and trust to the judicious reader to omit them altogether or to skim them as he feels inclined. The second part consists of five chapters, which are mostly histori- cal. They deal respectively with three classical problems in geometry| namely, the duplication of the cube, the trisection of an angle, and the quadrature of the circle|astrology, the hypotheses as to the nature of space and mass, and a means of measuring time. I have inserted detailed references, as far as I know, as to the sources of the various questions and solutions given; also, wherever I have given only the result of a theorem, I have tried to indicate authorities where a proof may be found. In general, unless it is stated otherwise, I have taken the references direct from the original works; but, in spite of considerable time spent in verifying them, I dare not suppose that they are free from all errors or misprints. I shall be grateful for notices of additions or corrections which may occur to any of my readers. W.W. ROUSE BALL Trinity College, Cambridge. February, 1892. NOTE TO THE FOURTH EDITION. In this edition I have inserted in the earlier chapters descriptions of several additional Recreations involving elementary mathematics, and I have added in the second part chapters on the History of the Mathe- matical Tripos at Cambridge, Mersenne's Numbers, and Cryptography and Ciphers. It is with some hesitation that I include in the book the chapters on Astrology and Ciphers, for these subjects are only remotely connected with Mathematics, but to afford myself some latitude I have altered the title of the second part to Miscellaneous Essays and Problems. W.W.R.B. Trinity College, Cambridge. 13 May, 1905. v TABLE OF CONTENTS. vi PART I. \Les hommes ne sont jamais plus ing´enieux que dans l'invention des jeux; l'esprit s'y trouve `a son aise. Apr`esles jeux qui d´ependent unique- ment des nombres viennent les jeux o`uentre la situ- ation. Apr`esles jeux o`un'entrent que le nombre et la situation viendraient les jeux o`uentre le mou- vement. Enfin il serait a souhaiter qu'on e^utun cours entier des jeux, trait´esmath´ematiquement." (Leibnitz: letter to De Montmort, July 29, 1715.) 1 CHAPTER I. SOME ARITHMETICAL QUESTIONS. The interest excited by statements of the relations between num- bers of certain forms has been often remarked. The majority of works on mathematical recreations include several such problems, which are obvious to any one acquainted with the elements of algebra, but which to many who are ignorant of that subject possess the same kind of charm that some mathematicians find in the more recondite proposi- tions of higher arithmetic. I shall devote the bulk of this chapter to these elementary problems, but I append a few remarks on one or two questions in the theory of numbers. Before entering on the subject of the chapter, I may add that a large proportion of the elementary questions mentioned here and in the following two chapters are taken from one of two sources. The first of these is the classical Probl`emesplaisans et d´electables, by C.G. Ba- chet, sieur de M´eziriac,of which the first edition was published in 1612 and the second in 1624: it is to the edition of 1624 that the references hereafter given apply. Several of Bachet's problems are taken from the writings of Alcuin, Pacioli di Burgo, Tartaglia, or Cardan, and possi- bly some of them are of oriental origin, but I have made no attempt to add such references. The other source to which I alluded above is Ozanam's R´ecr´eationsmath´ematiqueset physiques. The greater por- tion of the original edition, published in two volumes at Paris in 1694, was a compilation from the works of Bachet, Leurechon, Mydorge, van Etten, and Oughtred: this part is excellent, but the same cannot be said of the additions due to Ozanam. In the Biographie Universelle al- lusion is made to subsequent editions issued in 1720, 1735, 1741, 1778, 2 CH. I] ARITHMETICAL RECREATIONS. 3 and 1790; doubtless these references are correct, but the following edi- tions, all of which I have seen, are the only ones of which I have any knowledge. In 1696 an edition was issued at Amsterdam. In 1723| six years after the death of Ozanam|one was issued in three volumes, with a supplementary fourth volume, containing (among other things) an appendix on puzzles: I believe that it would be difficult to find in any of the books current in England on mathematical amusements as many as a dozen puzzles which are not contained in one of these four volumes. Fresh editions were issued in 1741, 1750 (the second volume of which bears the date 1749), 1770, and 1790. The edition of 1750 is said to have been corrected by Montucla on condition that his name should not be associated with it; but the edition of 1790 is the earliest one in which reference is made to these corrections, though the editor is referred to only as Monsieur M***. Montucla expunged most of what was actually incorrect in the older editions, and added several historical notes, but unfortunately his scruples prevented him from striking out the accounts of numerous trivial experiments and truisms which over- load the work. An English translation of the original edition appeared in 1708, and I believe ran through four editions, the last of them being published in Dublin in 1790. Montucla's revision of 1790 was translated by C. Hutton, and editions of this were issued in 1803, in 1814, and (in one volume) in 1840: my references are to the editions of 1803 and 1840. I proceed now to enumerate some of the elementary questions con- nected with numbers which for nearly three centuries have formed a large part of most compilations of mathematical amusements. They are given here mainly for their historical|not for their arithmetical| interest; and perhaps a mathematician may well omit them, and pass at once to the latter part of this chapter. These questions are of the nature of tricks or puzzles and I follow the usual course and present them in that form. I may note however that most of them are not worth proposing, even as tricks, unless either the modus operandi is disguised or the result arrived at is different from that expected; but, as I am not writing on conjuring, I refrain from alluding to the means of disguising the operations indicated, and give merely a bare enumeration of the steps essential to the success of the method used, though I may recall the fundamental rule that no trick, however good, will bear immediate repetition, and that, if it is 4 ARITHMETICAL RECREATIONS.
Load more

Recommended publications
  • About Cards & Puzzle
    Cards & Puzzle Fun Dozens of interesting card & $10 compelling puzzle games to play in solitude or against humans. Absolute Farkle Classic Mahjong Fashion Cents Deluxe A fun and easy to play dice game. Solitaire You are given a wide assortment But be careful, it is easy to get The objective of mahjong solitaire of hats, tops, bottoms, and shoes addicted. It also goes by other is simple – just removing the in a variety of styles and colors, names such as Ten Thousand and matching tiles. But there is a which you must combine into 6 Dice. simple rule that adds quite a bit outfits that are color-coordinated. of complexity to the game… White, black, and denim items are BombDunk Mahjong solitaire only lets you wild and go with any other color. Mixes the strategy of remove a tile if there isn't a tile Minesweeper with the cross- directly above it, or the tile can't GrassGames’ Cribbage checking logic of Sudoku, and slide to the left or right. Although A beautiful 3D computer game presents it in a fun arcade format. the rules are simple- the game version of the classic 400 year old The object of the game is to can require quite a bit of strategy card game for 2 players. With locate hidden Bombs without and forethought! Intelligent Computer opponents making too many mistakes! You or Full Network Play can work out where the bombs Classic Solitaire are with a combination of logical A fun and easy-to-use collection clues and a little guesswork.
    [Show full text]
  • The Zodiacus Vitae of Marcellus Palingenius Stellatus : an Old
    .THE ZODIACUS VITAE FOSTE THE LIBRARY OF THE UNIVERSITY OF CALIFORNIA LOS ANGELES Ex Lihris SIR MICHAEL SADLER ACQUIRED 1948 WITH THE HELP OF ALUMNI OF THE SCHOOL OF EDUCATION THE ZODIACUS VITAE Inscribed to my loyal friend, in school and ever since— ARTHUR CROOKES NEWSUM, B.A., Chairman of the Governors of the Lincoln Grammar School, heartily congratulating him, and rejoicing with him, on the opening of such New Buildings as would astound the pious Benefactors of our Old School—buildings which will be another glory to the glorious City of Lincoln, and hold forth the blessed hope of added intellectual possibilities to future generations, whose children will ever feel it their noble privi- lege to set forth in life, and, for the good of their country, to endeavour to walk worthily of the traditions of the Old School, " and of that beautiful and ancient City set on a Hill." University College of Wales, Aberystwyth. November, 1907. THE ZODIACUS VITAE OF MARCELLUS PALINGENIUS STELLATUS : An Old School-Book Described By FOSTER WATSON, M.A Professor of Education in the University College of Wales, Aberystwyth LONDON PHILIP WELLBY 6, HENRIETTA STREET, COVENT GARDEN, W.C 1908 BUTLER Sc TANNER, THE SELWOOD Printing Works, Frome, and londoh. Introduction The Zodiacus Vitae of Marcellus Palingenius is an old school-book used in English as well as foreign schools in the time of Shakespeare, At page 67, the Statutes of St. Bee's Grammar School (1583), in Cumberland, are cited as including Palingenius' Zodiacus Vitae. Other instances are the Orders made for St.
    [Show full text]
  • The Beautiful Cubit System I Douglas 2019 the Beautiful Cubit System
    The Beautiful Cubit System I Douglas 2019 The Beautiful Cubit System Ian Douglas, B.Sc [email protected] 30 June 2019 Version 1.0.0 DOI: https://doi.org/10.5281/zenodo.3263864 This work is licensed under the Creative Commons Attribution 4.0 International License. Abstract An analysis of the Egyptian Royal cubit, presenting some research and opinions flowing from that research, into what I believe was the original cubit, and how it was corrupted. I show various close arithmetic approximations and multiple ways of getting the divisions of the cubit, as well as some related measures. The cubit also encapsulates the basic components for the metric system. Keywords: Egyptology, metrology, royal cubit, cubit, metre, foot, metric system Contents 1. Introduction 2. Overview of current understanding 3. An alternative origin 4. Different ways of approximating the royal cubit 5. Different ways of getting the cubit divisions 6. Geometry, the Royal Cubit and the metric system 7. Bibliography 1. Introduction The cubit is a well-know ancient measure of length, used around various places in the Middle East and Mediterranean region in the distant past. 1 The Beautiful Cubit System I Douglas 2019 It is allegedly based on the length of a human (male) fore-arm. It is typically measured from the back of the elbow to some point between the wrist and the end of the outstretched middle finger, or in some variants, a point beyond that. The problem with this approach is that everyone’s arm is a different length. If the heights of the dynastic Egyptians is taken as representative, then their arms would have been too short to justify the accepted lengths.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • LIBRA - YOUR ZODIAC HOROSCOPE 2021 © Ganeshaspeaks.Com 2021 First Edition, 2021
    GaneshaSpeaks.com | 1 LIBRA - YOUR ZODIAC HOROSCOPE 2021 © GaneshaSpeaks.com 2021 First edition, 2021 Copyrighted 2020-2021 by GaneshaSpeaks.com. All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means – electronic, mechanical, printing, photocopying, recording, or otherwise – without prior written permission from GaneshaSpeaks.com. Any act of this sort, without permission, will be seen as direct plagiarism and shall be prosecutable by law and/ or specific acts. DISCLAIMER The material contained in this book is predictive and informative in nature. However, it may or may not apply to your peculiar situation and Personal Horoscope. We sincerely advise you to apply your discretion, keeping in mind your specific situation/needs, while following and adopting any of the zodiac related information or predictions given in this book. The information/ predictions provided in this book are based largely on the Sun-Sign (Western) system of Astrology. Please note that Astrology is an expansive area of study, and does not guarantee 100% accuracy. Thus, while meticulous care has been taken to present astrologically astute predictions, our team of authors, publisher and distributor/s do not provide any guarantee about the precision or exact applicability of the information that is, withal, generic in nature. The authors and publisher, therefore, do not assume, and hereby disclaim, any liability to any party for any misunderstanding, loss, damage or disruption caused by predictions and/or errors of omission or commission, regardless of whether such errors are a result of negligence, accident or any other cause. This book, moreover, is not meant to be a substitute for expert advice, including health predictions, and we explicitly propose that the reader consult relevant expert/s for any particular problem or challenge.
    [Show full text]
  • Annotated Bibliography for the Michigan Global/International Education Resource Center
    DOCUMENT RESUME ED 395 835 SO 024 959 AUTHOR Barr, E. Gene TITLE Annotated Bibliography for the Michigan Global/International Education Resource Center. INSTITUTION International Inst. of Flint, MI. Michigan Global/International Education Resource Center. SPONS AGENCY Center for Global Partnership Foundation.; Japanese Society of Detroit Foundation, MI.; United States-Japan Foundation. PUB DATE Jun 94 NOTE 116p. AVAILABLE FROM International Institute of Flint, 515 Stevens, Flint, MI 48502. PUB TYPE Reference Materials Bibliographies (131) EDRS PRICE MF01/PC05 Plus Postage. DESCRIPTORS Annotated Bibliographies; Area Studies; *Asian History; *Asian Studies; Cultural Background; Elementary Secondary Education; Foreign Countries; *Multicultural Education; *Non Western Civilization; Social Studies; World History IDENTIFIERS Japan; Michigan ABSTRACT This annotated bibliography on Japan serves as a useful compendium and guide to the holdings of the Michigan Global/International Education Resource Center, housed at the International Institute of Flint. The holdings will be disseminated throughout Michigan at workshops, seminars, and institutes. The bibliography includes background and instruction materials designed to foster multicultural, international, and global understandings in Michigan classrooms. The volume includes both print and non-print materials. Print materials include:(I) Background References--Books; (2) Background References--Newspapers, Journals, Maps, Brochures;(3) Exploratory Japanese-Language Instruction and Intensive Japanese Instruction Materials;(4) Curriculum Materials--Teacher and Student; and (5) Children's Literature and Literature Units. Eight appendices contains useful information for further research and reference use. (EH) ************ Reproductions supplied by EDRS are the best that can be made * from the original document. * ************************************************A.***********,-- ,-A Ink a : a° A 9 EWE : was liTangiltall111 1191.1 tin CI) OiC) kr) C- U S DEPARTMENT Or- EDUCATION TO REPRODUCE AND Ed ,c5ton i t no.
    [Show full text]
  • English-German Wordlist
    CUTTING EDGE Pre-intermediate - NEW EDITION English - German wordlist module p. no. exercise English phonetic German Sample sentence 1 1 6 leisure/lifestyle leisure ['leZə] Freizeit How do you spend your leisure time? 1 6 leisure/lifestyle lifestyle ['lafstal] Lebensstil They have a very exciting lifestyle. 1 6 voc.1a go clubbing [gəυ klöb] Nachtklubs besuchen Shall we go clubbing tonight? 1 6 voc.1a go for a run [gəυ fə ə rön] joggen, rennen Where's Dad? - He's gone for a run. 1 6 voc.1a skateboarding ['sketbɔ:d] Skateboard fahren Skateboarding is very popular at my school. 1 6 voc.1a snowboarding ['snəυbɔ:d] Snowboard fahren There is a section of the piste for snowboarding. 1 6 voc.1a rollerblading ['rəυlə"bled] Inlineskaten We went rollerblading in the park. 1 6 voc.1a skiing ['ski:] Skifahren We went skiing in Switzerland. 1 6 voc.1a surfing the internet ['sÆ:f] im Internet surfen He spends all evening surfing the internet. 1 6 voc.1a yoga ['jəυgə] Yoga She started a yoga class. 1 6 voc.1b what else [w}t _'els] was sonst noch That's a start, what else have you got? 1 7 voc.2 survey [sə've] Untersuchung The company carried out a survey of people's attitudes to housework. 1 7 voc.2 result [r'zölt] Ergebnis The whole situation was the result of a silly mistake. 1 7 voc.2 rent (v) [rent] ausleihen We rent the flat from my uncle. 1 7 voc.3 according to [ə'kɔ:d tu:] laut According to Rachel, Keith started the fight.
    [Show full text]
  • The CHARIOTEER ' a Quarterly Review of Modern Greek Culture Edited by Kimon Friar
    The CHARIOTEER ' A Quarterly Review of Modern Greek Culture Edited by Kimon Friar NUMBER 3 1961 PREFACE TO POPE JOAN by LAWRENCE DURRELL .from POPE JOAN by EMMANUEL RoYIDIS Small Anthologies of MICHAEL TOMBROS I. M. PANAYOTOPOULOS TAKIS PAPATZONIS DREAM AND REALITY IN SATIRE text and cartoons by Minos Argyrakis NAUSICAA AND ODYSSEUS by HOMER and by NIKOS KAZANTZAKIS TWO POEMS by c. A. TRYPANIS from the OEDIPUS plays by SoPHOCLES THE SPHINX'S RIDDLE TO OEDIPUS by RANDALL JARRELL OEDIPUS by RICHARD EBERHART Fiction and Essays by MINAS DIMAKIS GHIKA ZAHARIAS PAPANDONIOU EVANGELOS PAPANOUTSOS ANGHELOS PROKOPIOU CLEON PARASCHOS NELLY THEODOROU MICHAEL TOMBROS Published by Parnassos, Greek Cultural Society of New York Sr. so ACKNOWLEDGMENTS To The Anglo-Hellenic Review for excerpts The Odyssey, by Homer, copyright © 1961 from "The Poetry of Takis Papatzonis" by by Robert Fitzgerald. To E. P. Dutton and Cleon Paraschos. To The Arizona Quarterly, Company for "Preface," by Lawrence Dur­ Summer, 1955, for "Outline of Error," by rell and excerpts from Pope Joan, by Emman­ Takis Papatzonis, translation and copyright uel Royidis, translated from the Greek by ©by Kimon Friar. To Atheneum for "The Lawrence Durrell, revised edition, copy­ Sphinx's Riddle to Oedipus," from The right© 1961 by Lawrence Durrell. To Faber Woman at the Washington Zoo, copyright© & Faber Limited for excerpts from Oedipus 1960 by Randall Jarrell. To The Atlantic the King and Oedipus at Colonus, translation Monthly, June, 1955, for "Before the Ad­ and copyright© 1961 by C. P. Trypanis. vent," by Takis Papatzonis, translation and To The New Age for excerpts from "1.
    [Show full text]
  • English Customary Weights and Measures
    English Customary Weights and Measures Distance In all traditional measuring systems, short distance units are based on the dimensions of the human body. The inch represents the width of a thumb; in fact, in many languages, the word for "inch" is also the word for "thumb." The foot (12 inches) was originally the length of a human foot, although it has evolved to be longer than most people's feet. The yard (3 feet) seems to have gotten its start in England as the name of a 3-foot measuring stick, but it is also understood to be the distance from the tip of the nose to the end of the middle finger of the outstretched hand. Finally, if you stretch your arms out to the sides as far as possible, your total "arm span," from one fingertip to the other, is a fathom (6 feet). Historically, there are many other "natural units" of the same kind, including the digit (the width of a finger, 0.75 inch), the nail (length of the last two joints of the middle finger, 3 digits or 2.25 inches), the palm (width of the palm, 3 inches), the hand (4 inches), the shaftment (width of the hand and outstretched thumb, 2 palms or 6 inches), the span (width of the outstretched hand, from the tip of the thumb to the tip of the little finger, 3 palms or 9 inches), and the cubit (length of the forearm, 18 inches). In Anglo-Saxon England (before the Norman conquest of 1066), short distances seem to have been measured in several ways.
    [Show full text]
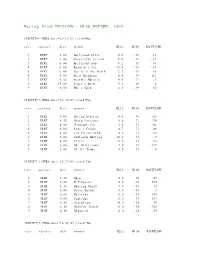
  • Racing Flow-TM FLOW + BIAS REPORT: 2009
    Racing Flow-TM FLOW + BIAS REPORT: 2009 CIRCUIT=1-NYRA date=12/31/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 5.50 Hollywood Hills 0.0 -19 13 2 DIRT 6.00 Successful friend 5.0 -19 -19 3 DIRT 6.00 Brilliant Son 5.2 -19 47 4 DIRT 6.00 Raynick's Jet 10.6 -19 -61 5 DIRT 6.00 Yes It's the Truth 2.7 -19 65 6 DIRT 8.00 Keep Thinking 0.0 -19 -112 7 DIRT 8.32 Storm's Majesty 4.0 -19 6 8 DIRT 13.00 Tiger's Rock 9.4 -19 6 9 DIRT 8.50 Mel's Gold 2.5 -19 69 CIRCUIT=1-NYRA date=12/30/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.00 Spring Elusion 4.4 71 -68 2 DIRT 8.32 Sharp Instinct 0.0 71 -74 3 DIRT 6.00 O'Sotopretty 4.0 71 -61 4 DIRT 6.00 Indy's Forum 4.7 71 -46 5 DIRT 6.00 Ten Carrot Nikki 0.0 71 -18 6 DIRT 8.00 Sawtooth Moutain 12.1 71 9 7 DIRT 6.00 Cleric 0.6 71 -73 8 DIRT 6.00 Mt. Glittermore 4.0 71 -119 9 DIRT 6.00 Of All Times 0.0 71 0 CIRCUIT=1-NYRA date=12/27/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.50 Quip 4.5 -38 49 2 DIRT 6.00 E Z Passer 4.2 -38 255 3 DIRT 8.32 Dancing Daisy 7.9 -38 14 4 DIRT 6.00 Risky Rachel 0.0 -38 8 5 DIRT 6.00 Kaffiend 0.0 -38 150 6 DIRT 6.00 Capridge 6.2 -38 187 7 DIRT 8.50 Stargleam 14.5 -38 76 8 DIRT 8.50 Wishful Tomcat 0.0 -38 -203 9 DIRT 8.50 Midwatch 0.0 -38 -59 CIRCUIT=1-NYRA date=12/26/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 6.00 Papaleo 7.0 108 129 2 DIRT 6.00 Overcommunication 1.0 108 -72 3 DIRT 6.00 Digger 0.0 108 -211 4 DIRT 6.00 Bryan Kicks 0.0 108 136 5 DIRT 6.00 We Get It 16.8 108 129 6 DIRT 6.00 Yawanna Trust 4.5 108 -21 7 DIRT 6.00 Smarty Karakorum 6.5 108 83 8 DIRT 8.32 Almighty Silver 18.7 108 133 9 DIRT 8.32 Offlee Cool 0.0 108 -60 CIRCUIT=1-NYRA date=12/13/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.32 Crafty Bear 3.0 -158 -139 2 DIRT 6.00 Cheers Darling 0.5 -158 61 3 DIRT 6.00 Iberian Gate 3.0 -158 154 4 DIRT 6.00 Pewter 0.5 -158 8 5 DIRT 6.00 Wolfson 6.2 -158 86 6 DIRT 6.00 Mr.
    [Show full text]
  • 1. Korean Zodiac the Chinese Zodiac Signs Are Used by Cultures Other Than Chinese, Too
    EDIÇÃO Nº 07 NOVEMBRO DE 2014 ARTIGO RECEBIDO ATÉ 30/09/2014 ARTIGO APROVADO ATÉ 30/10/2014 ZODIAC ANIMALS IN KOREAN PROVERBS Arevik Chačatrjan Charles University in Prague, Department of Ethnology, Prague, Czech Republic SUMMARY:There are a lot of animals we can meet in Korean folklore, but in this paper are described the animals that are most commonly mentioned in the Far Eastern zodiac, better known in English as the Chinese Zodiac. Here are described the role of the zodiac animal images in Korean folklore: proverbs, sayings etc. Each animal has its allegorical form and expresses various traits of man. Dealing with twelve animals of the Korean zodiac such as rat (jui), ox (so), tiger (beom, horangi), rabbit (tokki), dragon (yong), snake (baem), horse (mal), sheep (yang), monkey (wonsungi), rooster (sutak), dog (gae), pig (dwaeji), this article represents a contribution to research in Korean paremiology in the specific field of animal idioms. Besides referring to proverbs and sayings about these animals, surely I also try to give some examples of their role and importance in the history of the Korean nation and in other genres of Korean folklore. For this article, are used both North and South Korean sources, mainly dictionaries and books of proverbs, in order to disprove the point of view that there are profound big language differences between the two Koreas. 1. Korean zodiac The Chinese zodiac signs are used by cultures other than Chinese, too. They are used in some other Asian countries that have been under the cultural influence of China and also in countries that have not been under influence of China.
    [Show full text]
  • The English Measurement System
    THE ENGLISH MEASUREMENT SYSTEM The measurement system commonly used in the United States today is nearly the same as that brought by the colonists from England. These measures had their origins in a variety of cultures –Babylonian, Egyptian, Roman, Anglo-Saxon, and Norman French. The ancient "digit," "palm," "span" and "cubic" units of length slowly lost preference to the length units "inch," "foot," and "yard." Roman contributions include the use of 12 as a base number (the foot is divided into 12 inches) and the words from which we derive many of our present measurement unit names. For example, the 12 divisions of the Roman "pes," or foot were called unciae. Our words "inch" and "ounce" are both derived from that Latin word. The "yard" as a measure of length can be traced back to early Saxon kings. They wore a sash or girdle around the waist that could be removed and used as a convenient measuring device. The word "yard" comes from the Saxon word "gird" meaning the circumference of a person’s waist. Standardizing various units and combining them into loosely related systems of measurement units sometimes occurred in fascinating ways. Tradition holds that King Henry I decreed that a yard should be the distance from the tip of his nose to the end of his outstretched thumb. The length of a furlong (or furrow-long) was established by early Tudor rulers as 220 yards. This led Queen Elizabeth I to declare in the 16th century, that henceforth the traditional Roman mile of 5000 feet would be replaced by one of 5280 feet, making the mile exactly eight furlongs and providing a convenient relationship between the furlong and the mile.
    [Show full text]