Performance Portability of a Wilson Dslash Stencil Operator Mini-App Using Kokkos and SYCL
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

GPU Developments 2018
GPU Developments 2018 2018 GPU Developments 2018 © Copyright Jon Peddie Research 2019. All rights reserved. Reproduction in whole or in part is prohibited without written permission from Jon Peddie Research. This report is the property of Jon Peddie Research (JPR) and made available to a restricted number of clients only upon these terms and conditions. Agreement not to copy or disclose. This report and all future reports or other materials provided by JPR pursuant to this subscription (collectively, “Reports”) are protected by: (i) federal copyright, pursuant to the Copyright Act of 1976; and (ii) the nondisclosure provisions set forth immediately following. License, exclusive use, and agreement not to disclose. Reports are the trade secret property exclusively of JPR and are made available to a restricted number of clients, for their exclusive use and only upon the following terms and conditions. JPR grants site-wide license to read and utilize the information in the Reports, exclusively to the initial subscriber to the Reports, its subsidiaries, divisions, and employees (collectively, “Subscriber”). The Reports shall, at all times, be treated by Subscriber as proprietary and confidential documents, for internal use only. Subscriber agrees that it will not reproduce for or share any of the material in the Reports (“Material”) with any entity or individual other than Subscriber (“Shared Third Party”) (collectively, “Share” or “Sharing”), without the advance written permission of JPR. Subscriber shall be liable for any breach of this agreement and shall be subject to cancellation of its subscription to Reports. Without limiting this liability, Subscriber shall be liable for any damages suffered by JPR as a result of any Sharing of any Material, without advance written permission of JPR. -

Future-ALCF-Systems-Parker.Pdf
Future ALCF Systems Argonne Leadership Computing Facility 2021 Computational Performance Workshop, May 4-6 Scott Parker www.anl.gov Aurora Aurora: A High-level View q Intel-HPE machine arriving at Argonne in 2022 q Sustained Performance ≥ 1Exaflops DP q Compute Nodes q 2 Intel Xeons (Sapphire Rapids) q 6 Intel Xe GPUs (Ponte Vecchio [PVC]) q Node Performance > 130 TFlops q System q HPE Cray XE Platform q Greater than 10 PB of total memory q HPE Slingshot network q Fliesystem q Distributed Asynchronous Object Store (DAOS) q ≥ 230 PB of storage capacity; ≥ 25 TB/s q Lustre q 150PB of storage capacity; ~1 TB/s 3 The Evolution of Intel GPUs 4 The Evolution of Intel GPUs 5 XE Execution Unit qThe EU executes instructions q Register file q Multiple issue ports q Vector pipelines q Float Point q Integer q Extended Math q FP 64 (optional) q Matrix Extension (XMX) (optional) q Thread control q Branch q Send (memory) 6 XE Subslice qA sub-slice contains: q 16 EUs q Thread dispatch q Instruction cache q L1, texture cache, and shared local memory q Load/Store q Fixed Function (optional) q 3D Sampler q Media Sampler q Ray Tracing 7 XE 3D/Compute Slice qA slice contains q Variable number of subslices q 3D Fixed Function (optional) q Geometry q Raster 8 High Level Xe Architecture qXe GPU is composed of q 3D/Compute Slice q Media Slice q Memory Fabric / Cache 9 Aurora Compute Node • 6 Xe Architecture based GPUs PVC PVC (Ponte Vecchio) • All to all connection PVC PVC • Low latency and high bandwidth PVC PVC • 2 Intel Xeon (Sapphire Rapids) processors Slingshot -

Hardware Developments V E-CAM Deliverable 7.9 Deliverable Type: Report Delivered in July, 2020
Hardware developments V E-CAM Deliverable 7.9 Deliverable Type: Report Delivered in July, 2020 E-CAM The European Centre of Excellence for Software, Training and Consultancy in Simulation and Modelling Funded by the European Union under grant agreement 676531 E-CAM Deliverable 7.9 Page ii Project and Deliverable Information Project Title E-CAM: An e-infrastructure for software, training and discussion in simulation and modelling Project Ref. Grant Agreement 676531 Project Website https://www.e-cam2020.eu EC Project Officer Juan Pelegrín Deliverable ID D7.9 Deliverable Nature Report Dissemination Level Public Contractual Date of Delivery Project Month 54(31st March, 2020) Actual Date of Delivery 6th July, 2020 Description of Deliverable Update on "Hardware Developments IV" (Deliverable 7.7) which covers: - Report on hardware developments that will affect the scientific areas of inter- est to E-CAM and detailed feedback to the project software developers (STFC); - discussion of project software needs with hardware and software vendors, completion of survey of what is already available for particular hardware plat- forms (FR-IDF); and, - detailed output from direct face-to-face session between the project end- users, developers and hardware vendors (ICHEC). Document Control Information Title: Hardware developments V ID: D7.9 Version: As of July, 2020 Document Status: Accepted by WP leader Available at: https://www.e-cam2020.eu/deliverables Document history: Internal Project Management Link Review Review Status: Reviewed Written by: Alan Ó Cais(JSC) Contributors: Christopher Werner (ICHEC), Simon Wong (ICHEC), Padraig Ó Conbhuí Authorship (ICHEC), Alan Ó Cais (JSC), Jony Castagna (STFC), Godehard Sutmann (JSC) Reviewed by: Luke Drury (NUID UCD) and Jony Castagna (STFC) Approved by: Godehard Sutmann (JSC) Document Keywords Keywords: E-CAM, HPC, Hardware, CECAM, Materials 6th July, 2020 Disclaimer:This deliverable has been prepared by the responsible Work Package of the Project in accordance with the Consortium Agreement and the Grant Agreement. -

Marc and Mentat Release Guide
Marc and Mentat Release Guide Marc® and Mentat® 2020 Release Guide Corporate Europe, Middle East, Africa MSC Software Corporation MSC Software GmbH 4675 MacArthur Court, Suite 900 Am Moosfeld 13 Newport Beach, CA 92660 81829 Munich, Germany Telephone: (714) 540-8900 Telephone: (49) 89 431 98 70 Toll Free Number: 1 855 672 7638 Email: [email protected] Email: [email protected] Japan Asia-Pacific MSC Software Japan Ltd. MSC Software (S) Pte. Ltd. Shinjuku First West 8F 100 Beach Road 23-7 Nishi Shinjuku #16-05 Shaw Tower 1-Chome, Shinjuku-Ku Singapore 189702 Tokyo 160-0023, JAPAN Telephone: 65-6272-0082 Telephone: (81) (3)-6911-1200 Email: [email protected] Email: [email protected] Worldwide Web www.mscsoftware.com Support http://www.mscsoftware.com/Contents/Services/Technical-Support/Contact-Technical-Support.aspx Disclaimer User Documentation: Copyright 2020 MSC Software Corporation. All Rights Reserved. This document, and the software described in it, are furnished under license and may be used or copied only in accordance with the terms of such license. Any reproduction or distribution of this document, in whole or in part, without the prior written authorization of MSC Software Corporation is strictly prohibited. MSC Software Corporation reserves the right to make changes in specifications and other information contained in this document without prior notice. The concepts, methods, and examples presented in this document are for illustrative and educational purposes only and are not intended to be exhaustive or to apply to any particular engineering problem or design. THIS DOCUMENT IS PROVIDED ON AN “AS-IS” BASIS AND ALL EXPRESS AND IMPLIED CONDITIONS, REPRESENTATIONS AND WARRANTIES, INCLUDING ANY IMPLIED WARRANTY OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE, ARE DISCLAIMED, EXCEPT TO THE EXTENT THAT SUCH DISCLAIMERS ARE HELD TO BE LEGALLY INVALID. -

Intel® Desktop Board D33217GKE
Intel® Desktop Board D33217GKE Next Unit of Computing by Intel® • Superior processing and graphics • Stunningly small form factor • Advanced Technologies producT brief Next Unit of Computing by Intel® with Intel® Desktop Board D33217GKE 4” (10 cm) Think you know what small can do? Think again. No more compromising between performance, profile, and price. The Next Unit of Computing (NUC) is a tiny 4”×4”×2” computing device with the power of the 3rd generation Intel® Core™ i3 processor. Its lower power consumption enables innovative system designs and energy- efficient applications in places like digital signage, home entertainment, and portable uses. Superior processing and graphics Visibly smart graphics using the 3rd generation Intel® Core™ i3-3217U processor deliver amaz- ing performance and visually stunning graphics. Stunningly small form factor The 4”×4”×2” form factor unlocks a world of potential design applications, from digital signage and kiosks to portable innovations. 4” (10 cm) Advanced Technologies The NUC features two SO-DIMM sockets for expandability upto 16 GB of memory, two PCIe* mini-card connectors for flexible support of wireless and SSD configurations, BIOS vault tech- nology, fast boot and the Intel® Visual BIOS. The NUC also supports Intel® Anti-Theft™ Technol- ogy providing hardware intelligence designed to protect your device and its data if its lost or stolen. Intel® Core™ i3-3217U Processor Intel® QS77 Express Chipset 2 Intel® Desktop Board D33217GKE Features and Benefits 1 × USB 2.0 connector on the front panel -

Intro to Parallel Computing
Intro To Parallel Computing John Urbanic Parallel Computing Scientist Pittsburgh Supercomputing Center Copyright 2021 Purpose of this talk ⚫ This is the 50,000 ft. view of the parallel computing landscape. We want to orient you a bit before parachuting you down into the trenches. ⚫ This talk bookends our technical content along with the Outro to Parallel Computing talk. The Intro has a strong emphasis on hardware, as this dictates the reasons that the software has the form and function that it has. Hopefully our programming constraints will seem less arbitrary. ⚫ The Outro talk can discuss alternative software approaches in a meaningful way because you will then have one base of knowledge against which we can compare and contrast. ⚫ The plan is that you walk away with a knowledge of not just MPI, etc. but where it fits into the world of High Performance Computing. FLOPS we need: Climate change analysis Simulations Extreme data • Cloud resolution, quantifying uncertainty, • “Reanalysis” projects need 100 more computing understanding tipping points, etc., will to analyze observations drive climate to exascale platforms • Machine learning and other analytics • New math, models, and systems support are needed today for petabyte data sets will be needed • Combined simulation/observation will empower policy makers and scientists Courtesy Horst Simon, LBNL Exascale combustion simulations ⚫ Goal: 50% improvement in engine efficiency ⚫ Center for Exascale Simulation of Combustion in Turbulence (ExaCT) – Combines simulation and experimentation – -

Draft NISTIR 8320A, Hardware-Enabled Security
NISTIR 8320A Hardware-Enabled Security: Container Platform Security Prototype Michael Bartock Murugiah Souppaya Jerry Wheeler Tim Knoll Uttam Shetty Ryan Savino Joseprabu Inbaraj Stefano Righi Karen Scarfone This publication is available free of charge from: https://doi.org/10.6028/NIST.IR.8320A NISTIR 8320A Hardware-Enabled Security: Container Platform Security Prototype Michael Bartock Joseprabu Inbaraj Murugiah Souppaya Stefano Righi Computer Security Division AMI Information Technology Laboratory Atlanta, GA Jerry Wheeler Karen Scarfone Tim Knoll Scarfone Cybersecurity Uttam Shetty Clifton, VA Ryan Savino Intel Corporation Santa Clara, CA This publication is available free of charge from: https://doi.org/10.6028/NIST.IR.8320A June 2021 U.S. Department of Commerce Gina Raimondo, Secretary National Institute of Standards and Technology James K. Olthoff, Performing the Non-Exclusive Functions and Duties of the Under Secretary of Commerce for Standards and Technology & Director, National Institute of Standards and Technology National Institute of Standards and Technology Interagency or Internal Report 8320A 48 pages (June 2021) This publication is available free of charge from: https://doi.org/10.6028/NIST.IR.8320A Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by NIST, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. There may be references in this publication to other publications currently under development by NIST in accordance with its assigned statutory responsibilities. The information in this publication, including concepts and methodologies, may be used by federal agencies even before the completion of such companion publications. -

Cisco Enterprise Wireless
Cisco Enterprise Wireless Intuitive Wi-Fi starts here 2nd edition Preface 7 Authors 8 Acknowledgments 10 Organization of this book 11 Intended audience 12 Book writing methodology 13 What is new in this edition of the book? 14 Introduction 15 Intent-based networking 16 Introducing Cisco IOS® XE for Cisco Catalyst® wireless 18 Benefits of Cisco IOS XE 19 Cisco wireless portfolio 22 Infrastructure components 29 Introduction 30 Deployment mode flexibility 32 Resiliency in wireless networks 41 Wireless network automation 58 Programmability 61 Radio excellence 63 Introduction 64 802.11ax/Wi-Fi 6 66 High density experience (HDX) 71 Hardware innovations 77 Introduction 78 Dual 5 GHz radio 79 Modularity 83 Multigigabit 85 CleanAir-SAgE 87 RF ASIC - software defined radio 89 Innovative AP deployment solutions 91 Infrastructure security 97 Introduction 98 Securing the network 100 Securing the air 109 Encrypted Traffic Analytics (ETA) 114 WPA3 119 Policy 121 Introduction 122 Security policy 123 QoS policy 132 Analytics 145 Introduction 146 Enhanced experience through partnerships 148 Cisco DNA Center – wireless assurance 150 Cisco location technology explained 156 Cisco DNA Spaces 160 Migrating to Catalyst 9800 163 The Catalyst 9800 configuration model 164 Configuration conversion tools 168 Inter-Release Controller Mobility (IRCM) 171 Summary 175 The next generation of wireless 176 References 177 Acronyms 178 Further reading 183 Preface 8 Preface Authors In May 2018, a group of engineers from diverse backgrounds and geographies gathered together in San Jose, California in an intense week-long collaborative effort to write about their common passion, enterprise wireless networks. This book is a result of that effort. -

Content Creation Solution Brief
Content Creation Solution Brief Intel® NUC delivers stunning visuals and edge-of-your-seat performance in an ultra-small package. Powered by a visibly smart 3rd generation Intel® Core™ i5 processor on a 4-by-4 inch board and enclosed in a tiny case, the Intel NUC is big on performance yet surprisingly small in size. It’s an ideal form factor that can be easily transported to the studio, while packing the horsepower to record, mix, create, and play back amazing audio and video content. Intel NUC is the definitive crowd-pleaser for today’s prosumer. B007 Multiscreen Content Creaton Setup Technologies This section offers a guideline for the hardware and software needed to design Intel NUC into a small form factor prosumer solution. Included in Intel NUC Kit: • Intel NUC – DC53427HYE • VESA Bracket • Power Adapter Hardware Needed Quantity Item Manufacturer Model 1 Intel® NUC DC53427HYE Intel® Intel® Next Unit of Computing Kit DC53427HYE 2 Memory Any 4 GB DDR3 1600 SODIMM 1 Storage Intel Intel® Solid-State Drive 525 Series 240 GB mSATA 1 Intel® Centrino Wireless Intel Intel Centrino 6235 IEEE 802.11n Mini PCI Express* Bluetooth* 4.0 - Wi-Fi/Bluetooth Combo Adapter 2 Display Port Capable Displays Any Any 1 HDMI Capable Display Any Any 1 USB Audio Interface Any Any 2 Reference Monitor Speakers Any Any 1 External Storage Any Any USB or Network Attached Storage Software Needed Item Manufacturer Model Pro Tools* Avid® Technology, Inc. http://www.avid.com/ Windows* 7 Microsoft* http://windows.microsoft.com Note: For more information on the software listed in this table, contact the manufacturer of the software directly. -

Bringing Two SGET Standards Together
boards & solutions + Combined Print Magazine for the European Embedded Market November 06/15 COVER STORY: Modular embedded NUC systems with Qseven modules Bringing two SGET Standards together SPECIAL FEATURES: SPECIAL ISSUE Boards & Modules Industrial Control Industrial Communications Industrial Internet-of-Things VIEWPOINT Dear Readers, And once again its show time! Beside the exhibition Embedded World in springtime there is another import- ant event for the embedded com- munity in Germany: SPS IPC Drives in fall. This year this international exhibition for industrial automa- tion will be held from 24th to 26th of November in the Exhibition Cen- tre in Nuremberg. More than 1,600 exhibitors including all key players in this industry will present their innovations and trend-setting new products as well as future technolo- gies. Main focus of many exhibitors this year will be Industrie 4.0. To simplify it for visitors getting infor- mation about this important topic the organizer created for the first time the “Industrie 4.0 Area” in Hall 3A. In this area there will be the joint stand and forum “Automation meets IT” which will present data based business models as well as IT based automation solutions for the future digital production. The joint stand “MES goes Automation“ will show how the use of MES optimizes order processing and production processes. The special show space SmartFactory will demonstrate the multi-vendor intelligent factory of the future. Industry associations ZVEI in hall 2 and VDMA in hall 3 will offer competent lectures and panel discussions about actual topics. The joint stands “AMA Centre for Sensors, Test and Measurement” and VDMA´s “Machine Vision” in hall 4A as well as “Wireless in Automation” will inform visitors extensive about the respective topics. -

Intel Next Unit of Computing Kit DC53427HYE UCFF, 1 X Core I5 3427U / 1.8 Ghz, RAM 0 MB, No HDD, HD Graphics 4000, Gigabit LAN, No OS, Vpro, Monitor : None
Siewert & Kau Computertechnik GmbH Walter-Gropius-Str. 12a DE 50126 Bergheim Telephone: 02271 - 763 0 Fax: 02271 - 763 280 E-Mail: [email protected] Internet: http://www.siewert-kau.com Intel Next Unit of Computing Kit DC53427HYE UCFF, 1 x Core i5 3427U / 1.8 GHz, RAM 0 MB, no HDD, HD Graphics 4000, Gigabit LAN, no OS, vPro, Monitor : none. A revolution in ultra-compact device design, Intel NUC packages a fully scalable, computing solution in the smallest possible form factor, complete with the Intel Core i5 processor. This computing device provides a flexible, customizable engine to drive digital signage, kiosks, and intelligent computing for small spaces, or anywhere else you can imagine. General information Intel Category Desktops & Servers Article number 103267 BOXDC53427HYE Technical specifications Product Description Intel Next Unit of Computing Kit DC53427HYE - Core i5 3427U 1.8 GHz - Monitor : none. Type PC barebone Platform Technology Intel vPro Technology Form Factor Ultra compact form factor Processor 1 x Intel Core i5 (3rd Gen) 3427U / 1.8 GHz ( 2.8 GHz ) ( Dual-Core ) Processor Main Features Hyper-Threading Technology, Intel Execute Disable Bit, Enhanced Intel SpeedStep Technology, Intel Virtualization Technology, Intel Turbo Boost Technology 2, Intel 64 Technology Cache Memory 3 MB Cache Per Processor 3 MB RAM 0 MB (installed) / 16 GB (max) - DDR3 SDRAM Hard Drive No HDD Monitor None. Graphics Controller Intel HD Graphics 4000 Audio Output Integrated - 7.1 channel surround Networking Gigabit LAN OS Provided No operating -
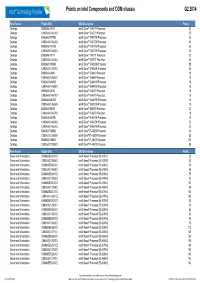
Q2 Matrix Final.Xlsx
Points on Intel Components and ODM chassis Q2 2014 Form Factor Eligble SKU SKU Description Points Desktop BX80646I74770 Intel® Core™ i7-4770 Processor 30 Desktop CM8064601464303 Intel® Core™ i7-4770 Processor 28 Desktop BX80646I74770K Intel® Core™ i7-4770K Processor 32 Desktop CM8064601464206 Intel® Core™ i7-4770K Processor 30 Desktop BX80646I74770S Intel® Core™ i7-4770S Processor 30 Desktop CM8064601465504 Intel® Core™ i7-4770S Processor 28 Desktop BX80646I74771 Intel® Core™ i7-4771 Processor 30 Desktop CM8064601464302 Intel® Core™ i7-4771 Processor 28 Desktop BX80633I74930K Intel® Core™ i7-4930K Processor 55 Desktop CM8063301292702 Intel® Core™ i7-4930K Processor 53 Desktop BX80646I54440 Intel® Core™ i5-4440 Processor 18 Desktop CM8064601464800 Intel® Core™ i5-4440 Processor 16 Desktop BX80646I54440S Intel® Core™ i5-4440S Processor 18 Desktop CM8064601465804 Intel® Core™ i5-4440S Processor 16 Desktop BX80646I54570 Intel® Core™ i5-4570 Processor 18 Desktop CM8064601464707 Intel® Core™ i5-4570 Processor 16 Desktop BX80646I54570S Intel® Core™ i5-4570S Processor 18 Desktop CM8064601465605 Intel® Core™ i5-4570S Processor 16 Desktop BX80646I54670 Intel® Core™ i5-4670 Processor 20 Desktop CM8064601464706 Intel® Core™ i5-4670 Processor 18 Desktop BX80646I54670K Intel® Core™ i5-4670K Processor 22 Desktop CM8064601464506 Intel® Core™ i5-4670K Processor 20 Desktop CM8064601465703 Intel® Core™ i5-4670S Processor 20 Desktop BX80633I74820K Intel® Core™i7-4820K Processor 30 Desktop CM8063301292805 Intel® Core™i7-4820K Processor 28 Desktop BX80633I74960X