Towards Fully Automatic Optimal Shape Modeling Karlsson, Johan
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Granat Family History
The Granat Family History by Virginia Mapes March 17, 2012 Sweden The number of Swedes doubled between 1750 and 1850, and the growth continued. In a country with few industries and cities, the burden had to be carried by the primitive agricultural society. At the end of the 1860s, Sweden was struck by the last of a series of severe hunger catastrophes. The agriculture which was still only partially modernized had been struggling with difficult times. Now came a series of crop failures. 1867 thus became "the wet year" of rotting grain, 1868 became the "dry year" of burned fields, and 1869 became "the severe year" of epidemics and begging children. Sixty thousand people left Sweden during these three "starvation years." It was the beginning of the mass emigration which, with short intervals, was to continue up to World War I. (Written by Ulf Beijbom) John Richard Karlsson Per (John) Richard Karlsson was born May 24, 1882 in Hova, Sweden to Karl Karlsson and Lovisa Johansdotter. [Richard’s last name was changed from Karlsson to Granat when he was in the Swedish Military Service in 1905.] Richard recalled walking the trails to school. However when winter came and the snow was deep, he would ski to school. It was so much faster because he could ski over the tops of the fences creating a shorter route. Richard’s childhood years in Sweden are somewhat vague. He had a sister Ellen and there may have been other brothers and sisters. They were a very poor farm family. Richard remembered that he and the other children in the family were always hungry, for these were the starvation years for the farm workers. -

Style Specifications
Site Soundscapes Landscape architecture in the light of sound Per Hedfors Department of Landscape Planning Ultuna Uppsala Doctoral thesis Swedish University of Agricultural Sciences Uppsala 2003 Acta Universitatis Agriculturae Sueciae Agraria 407 ISSN 1401-6249 ISBN 91-576-6425-0 © 2003 Per Hedfors, Uppsala Tryck: SLU Service/Repro, Uppsala 2003 Abstract Hedfors, Per. 2003. Site Soundscapes – landscape architecture in the light of sound. Doctor’s dissertation. issn 1401-6249, isbn 91-576-6425-0. This research was based on the assumption that landscape architects work on pro- jects in which the acoustic aspects can be taken into consideration. In such projects activities are located within the landscape and specific sounds belong to specific activities. This research raised the orchestration of the soundscape as a new area of concern in the field of landscape architecture; a new method of approaching the problem was suggested. Professionals can learn to recognise the auditory phenom- ena which are characteristic of a certain type of land use. Acoustic sources are obvious planning elements which can be used as a starting point in the develop- ment process. The effects on the soundscape can subsequently be evaluated according to various planning options. The landscape is viewed as a space for sound sources and listeners where the sounds are transferred and coloured, such that each site has a specific soundscape – a sonotope. This raised questions about the landscape’s acoustic characteristics with respect to the physical layout, space, material and furnishing. Questions related to the planning process, land use and conflicts of interest were also raised, in addition to design issues such as space requirements and aesthetic considerations. -
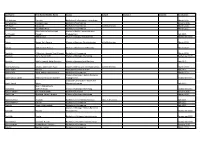
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation A/L Krishnan Thiinash Bachelor of Information Technology March 2015 A/L Selvaraju Theeban Raju Bachelor of Commerce January 2015 A/P Balan Durgarani Bachelor of Commerce with Distinction March 2015 A/P Rajaram Koushalya Priya Bachelor of Commerce March 2015 Hiba Mohsin Mohammed Master of Health Leadership and Aal-Yaseen Hussein Management July 2015 Aamer Muhammad Master of Quality Management September 2015 Abbas Hanaa Safy Seyam Master of Business Administration with Distinction March 2015 Abbasi Muhammad Hamza Master of International Business March 2015 Abdallah AlMustafa Hussein Saad Elsayed Bachelor of Commerce March 2015 Abdallah Asma Samir Lutfi Master of Strategic Marketing September 2015 Abdallah Moh'd Jawdat Abdel Rahman Master of International Business July 2015 AbdelAaty Mosa Amany Abdelkader Saad Master of Media and Communications with Distinction March 2015 Abdel-Karim Mervat Graduate Diploma in TESOL July 2015 Abdelmalik Mark Maher Abdelmesseh Bachelor of Commerce March 2015 Master of Strategic Human Resource Abdelrahman Abdo Mohammed Talat Abdelziz Management September 2015 Graduate Certificate in Health and Abdel-Sayed Mario Physical Education July 2015 Sherif Ahmed Fathy AbdRabou Abdelmohsen Master of Strategic Marketing September 2015 Abdul Hakeem Siti Fatimah Binte Bachelor of Science January 2015 Abdul Haq Shaddad Yousef Ibrahim Master of Strategic Marketing March 2015 Abdul Rahman Al Jabier Bachelor of Engineering Honours Class II, Division 1 -

Carlson Magazine Fall 2019
CARLSON THECARLSONSCHOOL OFMANAGEMENT MAGAZINEFORALUMNI ANDFRIENDS SCHOOL 100 YEARS OF The CARLSON School Centennial Celebration Weekend The Carlson School celebrated its centennial September 13 and 14 with events at U.S. Bank Stadium and during Gopher Game Day at TCF Bank Stadium. Check out pages 54�55 and carlsonschool.umn.edu for more coverage of the weekend. UNIVERSITYOFMINNESOTA CONTENT INTHISISSUE STARTUPNEWSBRIEFS CARLSONSCHOOLPARTNERSHIPHELPSKEEP LAKESCLEAN PEOPLEQUESTIONS CREATINGAMERICA'S FIRSTMISDEPARTMENT ALUMNIWHOMADEHISTORY ENGAGEMENT&GIVING NEWS&NOTES ALUMNIHAPPENINGS CLASSNOTES THINGSI’VELEARNEDSHELLEYNOLDEN FEATURES FROMTHEDEAN FACESOFCARLSON GORDONDAVIS&THEHISTORYOFMIS ATTHECARLSONSCHOOL STUDENTSLEARNINGFROMEXPERIENCE EXECUTIVESPOTLIGHT WHYEVERYCARLSONSCHOOL JIMOWENSCEOH B FULLER UNDERGRADSTUDIESABROAD THEIMPORTANCEOFGLOBALLEARNING FALL |CARLSONSCHOOLOFMANAGEMENT THECARLSONSCHOOL Asia Centennial Forum OFMANAGEMENT More than 150 alumni gathered in Shanghai for the Asia Centennial Forum in June. MAGAZINEFOR This exciting two-day event featured world-renowned Carlson School faculty, Asian ALUMNIANDFRIENDS business leaders, and alumni thought leaders discussing some of the most pressing business issues of the day. The event concluded with a Saturday evening gala. MAGAZINEEDITORS James Plesser Andre Eggert MAGAZINEDESIGN Daniele Lanza Nick Khow CONTRIBUTING WRITERS Taylor Hugo, Wade Rupard, Patrick Stephenson, Kate Westlund CONTRIBUTING PHOTOGRAPHERS Hannah Pietrick, Jeff Thompson ©2019 by the Regents of -
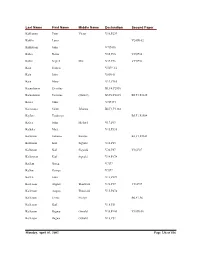
Delta County Naturalization Name Index
Last Name First Name Middle Name Declaration Second Paper Kahkonen Peter Victor V16,P239 Kahllo Louis V24,P102 Kahlstrom John V7,P436 Kahra Reino V35,P36 V35,P36 Kahra Segred Mrs. V35,P36 V35,P36 Kain Francis V5,P9 1/2 Kain John V8,P101 Kain Mary V19,P165 Kainulainen Eventius B1,F4,P2930 Kainulainen Eventius (Daniel) B5,F2,P2635 B5,F1,P2635 Kaiser John V7,P434 Kaivosoja Saimi Johanna B2,F1,P3144 Kajfasz Teodozya B5,F1,P2584 Kalies John Michael V17,P63 Kalkala Matt V15,P336 Kallarson Johanna Katrina B3,F1,P2101 Kallarson Karl Sigvald V18,P83 Kallarson Karl Sigwald V36,P87 V36,P87 Kallarsson Karl Sigvald V14,P178 Kallem Goreg V7,P7 Kallen George V7,P7 Kallen John V13,P329 Kallerson August Thorwald V31,P37 V31,P37 Kallerson August Thouvald V15,P474 Kallerson Jennie Evelyn B6,F1,P6 Kallerson Karl V18,P51 Kallerson Ragnar Oswald V35,P100 V35,P100 Kallerson Ragnar Oswald V18,P52 Monday, April 01, 2002 Page 236 of 536 Last Name First Name Middle Name Declaration Second Paper Kallersson Karl V38,P6 V38,P6 Kallin John V30,P78 V30,P78 Kallin Peter V26,P55 V26,P55 Kallin Peter V12,P480 Kallio Elma Wilhelmina B1,F4,P2987 Kallio Elma Wilhemiina B4,F4,P2509 B4,F4,P2509 Kallio Johan Victor B1,F3,P2876 Kallio Johan Vihtori B4,F4,P2448 B4,F4,P2448 Kallman And V12,P168 Kallman John V12,P167 Kallman John V7,P267 Kallman John V24,P110 Kallman John V20,P185 Kallman Lars E. V12,P79 Kallorssen Johanna B3,F1,P2101 Kalorssen Karl V38,P6 V38,P6 Kalsen Johannes V11,P171 Kamarainen Seth V15,P420 Kamarainen Seth V19,P92 Kamb Andre V8,P419 kAmerson Andrew V8,P426 Kaminen Oskar V31,P93 V31,P93 Kaminen Oskar V15,P167 Kamovich Mark V17,P284 Kampe Herman V5,P31 Kampe John E. -

Business Name Phone Email Address 1 City Business Description Certification Type
Business Name Phone Email Address 1 City Business Description Certification Type Janitorial cleaning,office cleaning, window cleaning, carpet extraction and cleaning, floor sealing and stripping, emergency 1 Clean Conscience 612-702-9603 [email protected] 15478 Pennock Lane Apple Valley clean up, power washing and more. SBE Janitorial cleaning,office cleaning, window cleaning, carpet extraction and cleaning, floor sealing and stripping, emergency 1 Clean Conscience 612-702-9603 [email protected] 15478 Pennock Lane Apple Valley clean up, power washing and more. WBE NAICS 811121: Automotive Body, Paint, and Interior Repair and Maintenance; NAICS 811198: All Other Automotive 1 Stop Auto Care, LLC 651-292-1485 [email protected] 159 W. Pennsylvania Avenue Saint Paul Repair and Maintenance MBE NAICS 811121: Automotive Body, Paint, and Interior Repair and Maintenance; NAICS 811198: All Other Automotive 1 Stop Auto Care, LLC 651-292-1485 [email protected] 159 W. Pennsylvania Avenue Saint Paul Repair and Maintenance SBE 1Source Holdings, LLC 612-868-1743 [email protected] 4250 Norex Drive Chaska Office Furniture Store SBE Architectural and interior planning and 292 Design Group Inc 612-767-3773 [email protected] 3533 East Lake Street Minneapolis design SBE NAICS 561720: Building cleaning services, 2nd 2none janitorial LLC 612-702-1250 [email protected] 2700 Plymonth ave north apt 2Minneapolis janitorial MBE NAICS 561720: Building cleaning services, 2nd 2none janitorial LLC 612-702-1250 [email protected] 2700 Plymonth ave north apt 2Minneapolis janitorial SBE Landscaping, Janitorial, Flooring, Cabinet 3 Chicks & A Hammer 612-701-9116 [email protected] 1800 Queen Ave No Minneapolis installation, Counter top installation. -

Club Name Last Name First Name Age Group Division Total 0Tri1 Triathlon Team Como 1 Papagallo Andrea M30-34 V 1. FC Kaiserslaute
Club Name Last Name First Name Age Group Division Total 0Tri1 Triathlon Team Como 1 Papagallo Andrea M30-34 V 1. FC Kaiserslautern Triathlon 1 Becker Arno M50-54 V 1. Triathlon Club Oldenburg Die Bären 1 Berdjis Navid M50-54 V 2tri 1 Badensø Kenneth M40-44 V 3bike.ch | Team 1 Denyes Jenna F30-34 IV 3City Triathlon 2 Wendelius Ludvig M30-34 IV Adolfsson Peter M50-54 IV 3D Fitness Race Team 1 Mcgirl Louise F45-49 V 3D Triathlon Vietnam 1 Nguyen Tuan M40-44 V 3K Sport 1 Komac Marko M45-49 IV 3MD 6 De Beul Bart M50-54 IV Claus Dieter M35-39 IV D'Haese Kevin M35-39 IV De Smet Laurens M30-34 IV De Rybel Ruud M25-29 IV Van Langenhove Simon M25-29 IV 21CC Triatloniklubi 2 Hääl Indrek M40-44 IV Rosen Ulf M50-54 IV 338 Småland Triathlon & Multisport 1 Bergqvist Mikael M55-59 IV /tri club denmark 63 Karlsson Alexander M25-29 II Bussek-Sedzinski Alexandra F35-39 II Eriksen Allan M40-44 II Eriksen Anders Wøhlk M35-39 II Fernandes Quilelli Andres Eduardo M25-29 II Blicher Anette F60-64 II Christiansen Anna-Marie F30-34 II Klærke-Olesen Anne Leth F30-34 II Poulsen Bjarne M55-59 II Skovgaard Pedersen Camilla F40-44 II Thorsen Christian Munch M50-54 II Petersen Claus M55-59 II Rindshoej Claus M50-54 II Larsen Claus Wiegand M55-59 II Hammarbro Ligaard Daniel M40-44 II Maman David M40-44 II Christensen Dennis M40-44 II Hansen Dorthe F35-39 II Olsen Frank M55-59 II Bruun Axelsen Henrik M45-49 II Larsen Henrik M50-54 II Rudolf Henrik M45-49 II Francke Christensen Jacob M35-39 II Olsen Jacob M30-34 II Thomsen Jakob M40-44 II Reichl Jan M50-54 II Gerlach Jan-Peter -

Genealogical Queries
Swedish American Genealogist Volume 14 Number 1 Article 5 3-1-1994 Genealogical Queries Follow this and additional works at: https://digitalcommons.augustana.edu/swensonsag Part of the Genealogy Commons, and the Scandinavian Studies Commons Recommended Citation (1994) "Genealogical Queries," Swedish American Genealogist: Vol. 14 : No. 1 , Article 5. Available at: https://digitalcommons.augustana.edu/swensonsag/vol14/iss1/5 This Article is brought to you for free and open access by the Swenson Swedish Immigration Research Center at Augustana Digital Commons. It has been accepted for inclusion in Swedish American Genealogist by an authorized editor of Augustana Digital Commons. For more information, please contact [email protected]. Genealogical Queries Genealogical queries from subscribers to Swedish American Genealogist will be listed here free of charge on a "space available" basis. The editor reserves the right to edit these queries to conform to a general format. The enquirer is responsible for the contents of the query. Svensson, Svensdotter I am trying to trace a group of six siblings who emigrated to America: 1. Anna Wilhelmina Svensdotter, b. in Gränna 12 Oct. 1857; emigr. from Gränna 8 May 1875. Probably deceased by the time the mother's estate inventory (bouppteckning) was held 1898. 2. Carl August Svensson, b. in Gränna 15 Sept. 1861; emigr. to New York 3 June 1881. 3. Emma Svensdotter, b. in Gränna 7 Dec. 1863; emigr. 5 May 1880. 4. Gustaf Svensson, b. in Gränna 8 June 1866; emigr. 22 Oct. 1889. 5. Alfred Svensson, b. in Gränna 31 Oct. 1870; emigr. from Adelöv Parish (Jön.) 29 Dec. 1890. -

JOCKUM NORDSTRÖM Biography 1963 Born in Stockholm, Sweden
JOCKUM NORDSTRÖM Biography 1963 Born in Stockholm, Sweden Lives in Stockholm Education The University College of Arts, Crafts and Design, Stockholm, Sweden Selected Awards and Fellowships 2015 Foundation Daniel & Florence Guerlain Contemporary Drawing Prize, France 2002 Watercolour Award, Konstakademien, Stockholm, Sweden 1999 Becker Artist Prize, Stockholm, Sweden Elsa Beskow Plaketten, Svensk Biblioteksförening, Stockholm, Sweden 1998 Heffaklumpen Children’s Book Prize awarded by Expressen Newspaper, Stockholm, Sweden Stora Svenska Illustratörspriset, Stockholm, Sweden 1995 Carl Larsson Stipendiet, The Royal Academy of Arts, Stockholm, Sweden Solo Exhibitions 2021 De osynligas väg / The Path of the Invisibles, Galleri Magnus Karlsson, Stockholm Pour ne pas dormir, La Criée centre d'art contemporain, Rennes, France 2020 Vem gick I trappan?/ Who Came in the Stairs?, Tegnerforbundet, Oslo, Norwa Jockum Nordstrom, La Crieé Centre d’Art Contemporain, Rennes, France Without Lantern, Skissernas Museum, Lund, Sweden 2019 The Anchor Hits the Sand, David Zwirner, London, UK 2018 Jockum Nordström: Why Is Everything A Rag, Contemporary Arts Center New Orleans, New Orleans, LA 2017 Jockum Nordström, Zeno X Gallery, Antwerp, Belgium 2016 När ingen vandrar vägen fram, då vandrar vägen själv sitt damm, Galleri Magnus Karlsson, Stockholm, Sweden 2014 For the insects and the hounds, David Zwirner, London, UK 2013 Jockum Nordström: Begin, Began, Begun, Anthony Meier Fine Arts, San Francisco, CA Jockum Nordstrom: All I Have Learned and Forgotten Again, -

Index of Names
Index of names Aardal, Bernt 257, 265 Binotto, Marco 341, 350 Abdeslam, Salah 133, 143, 148 Birkland, Thomas 225 Adam, Barbara 270, 283 Blais, Jean-Guy 112 Adamic, Lada A. 293, 307 Blum-Kulka, Shoshana 285 Ahlborg, Gunnar 246 Blum, Roger 331 Ahven, Andri 275, 284 Bock-Côté, Mathieu 183 Åker, Patrik 79, 285 Boczkowski, Pablo J. 65, 78, 86, 110 Albæk, Erik 265 Boileau, Anna 347, 350 Almeida Santos Clara 207 Bonfadelli, Heinz 331 Altheide, David L. 11, 18, 21, 24, 31, 56-58, 62, 67, Boomgaarden, Hajo 334, 350 77, 191-92, 206, 335, 350 Boorstin, Daniel J. 87, 110 Amelie, Maria 253-57, 259-61, 263-64 Borge-Holthoefer, Javier 293, 309 Ananny, Mike 309 Bosk, Charles. L. 88, 111, 193, 207, 292, 295, 309 Anderson, Ashley A. 307 boyd, danah 293, 307, 309 Anderson, CW 62, 65, 77 Boydstun, Amber E. 21, 25, 27, 32, 61-62, 64, 78, Anderson, Jørgen Goul 164 135, 137, 147, 151, 163, 212, 231, 236, 245, 268, Antonissen Dimitri 138, 140-41, 143-45 291, 307 Asp, Kent 62, 77 Brants, Kees 65, 67, 70, 72, 75, 78 Auch, Adam 25, 27, 31, 115, 127-29 Breed, Warren 86, 110 Augoustinos, Martha 254, 264 Brehm, John 233-34, 245 Augustinus, Liesbeth 78, 80 Brin, Colette 25, 28, 33, 167, 179, 183, 185, 335, 351 Backstrom, Lars 303, 309 Broersma, Marcel 66, 78 Bae, Soo Y. 294, 310 Brosius, Hans-Bernd 18, 33, 83-84, 86, 88-89, Ball-Rokeach, Sandra 214, 225 110, 141, 148, 182, 183, 194, 207, 299, 308 Ballone, Andrea 343, 350 Brossard, Dominique 83, 112, 291, 307 Banks, Mark 192, 206 Brown, Halina S. -
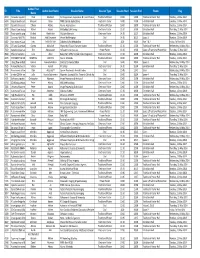
ID Title Author First Name Author Last Name Session Name Session
Author First ID Title Author Last Name Session Name Session Type Session Start Session End Room Day Name 4723 Fat‐water separatio Riad Ababneh Fat Suppression, Separation & Quantification Traditional Poster 10:00 12:00 Traditional Poster Hall Tuesday, 13 May 2014 5084 Capsaicin induced Maryam Abaei fMRI: Clinical Applications Electronic Poster 16:00 17:00 Exhibition Hall Tuesday, 13 May 2014 5927 Quantitative cereb Zaheer Abbas Neuro: Applications Traditional Poster 16:00 18:00 Traditional Poster Hall Tuesday, 13 May 2014 4038 Worst‐Case Analys Mahdi Abbasi MR Safety & RF Arrays Electronic Poster 13:30 14:30 Exhibition Hall Thursday, 15 May 2014 7008 Tract‐specific q‐spa Khaled Abdel‐Aziz Multiple Sclerosis Electronic Poster 14:15 15:15 Exhibition Hall Monday, 12 May 2014 6192 Coronary Wall Thic Khaled Abd‐Elmoniem Vessel Wall Imaging Oral 14:15 16:15 Space 3 Monday, 12 May 2014 5882 Non Invasive Quan Inès ABDESSELAM Diabetes & Fat Metabolism Oral 8:00 10:00 Blue 1 & 2Friday, 16 May 2014 1700 DTI and Quantitativ Osama Abdullah Myocardial Tissue Characterization Traditional Poster 13:30 15:30 Traditional Poster Hall Wednesday, 14 May 2014 7922 Gated Compensati Eric Aboussouan Diffusion Controversies Power Poster 13:30 14:30 Space 1/Traditional Poster Hall Thursday, 15 May 2014 4500 Effect of secretin st Julie Absil Body DWI/ MRS/ Female Pelvis Pregnancy Electronic Poster 17:30 18:30 Exhibition Hall Monday, 12 May 2014 4470 POSTMORTEM MR MARTINA ABSINTA Neuro: Methods Traditional Poster 16:00 18:00 Traditional Poster Hall Tuesday, 13 May -

Effect of Larval Diet on Endogenous Carbon Reproductive
EFFECT OF LARVAL DIET ON ENDOGENOUS CARBON REPRODUCTIVE RESOURCES OF FIFTH INSTARS AND ADULT FEMALES OF THE MOTH, HELIOTHIS VIRESCENS A Thesis Submitted to the Graduate Faculty of the North Dakota State University of Agriculture and Applied Science By Smita Dutta Suman In Partial Fulfillment for the Degree of MASTER OF SCIENCE Major Program: Entomology October 2013 Fargo, North Dakota North Dakota State University Graduate School Title Effect of larval diet on endogenous carbon reproductive resources of fifth instars and adult females of the moth Heliothis virescens. By Smita Dutta Suman The Supervisory Committee certifies that this disquisition complies with North Dakota State University’s regulations and meets the accepted standards for the degree of MASTER OF SCIENCE SUPERVISORY COMMITTEE: Stephen Foster Chair Kendra Geenlee Marion Harris Jason Harmon Approved: 11-07-13 Frank Casey Date Department Chair ABSTRACT Mostly adult Lepidoptera feed on plant nectar. That is, adults can only contribute to carbon, and not nitrogen, acquisition. The moth Heliothis virescens were used to explore the hypothesis that larval nutrition influences various adult carbon pools and that these, in turn, may affect pheromone production quantitatively. H. virescens larvae were reared on diets differing in carbohydrate, fat or protein content and resulting 5th instars and adults were analyzed for carbon pools, hemolymph trehalose concentration (HTC) and lipid content. Across all the diet treatments, changes in carbohydrate content affected carbon pool the most. In particular, for insects reared on a high carbohydrate diet, adults had a greater lipid content, while for insects reared on a low carbohydrate diet, adults had a lower HTC, compared to insects reared on the control or other diets.