DOCSLIB.ORG

Adaptive CORDIC: Using Parallel Angle Recoding to Accelerate CORDIC Rotations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Adaptive CORDIC: Using Parallel Angle Recoding to Accelerate CORDIC Rotations Copyright by Terence Keith Rodrigues 2007 The Dissertation Committee for Terence Keith Rodrigues certifies that this is the approved version of the following dissertation : Adaptive CORDIC: Using Parallel Angle Recoding to Accelerate CORDIC Rotations Committee: Earl E. Swartzlander, Jr., Supervisor Anthony P. Ambler Sudhir Dhawan Mircea D. Driga. Nur A. Touba Adaptive CORDIC: Using Parallel Angle Recoding to Accelerate CORDIC Rotations by Terence Keith Rodrigues, B.E.; M.S. Dissertation Presented to the Faculty of the Graduate School of The University of Texas at Austin in Partial Fulfilment of the Requirements for the Degree of Doctor of Philosophy The University of Texas at Austin December 2007 Dedication I dedicate this dissertation to my parents Anthony and Virginia Rodrigues, to my sister Lorraine and to my grand aunt ‘Fat-Mama’. Acknowledgements As I write this acknowledgement, I am excited at the thought that I am so close to achieving what will be one of the major milestones in my life. Having come this far, it is only fitting that I pay tribute to those who have supported me on this long journey. Dr Swartzlander, thank you for being my advisor, my mentor and above all a gentleman. After having gone through the process, I can truly appreciate the adage that choosing the right guide is the single most important decision in the Ph.D. process, and in retrospect I know I made the right choice. My warmest thanks to the members of my committee for your guidance and help, and for being a part of my supporting team as I undertook this long journey towards the Ph.D. I would like to acknowledge Dr Hyuk Park for his unstinting help in setting up the power and Verilog simulations, as well as Fred Graz and Michael Amundson for answering the many questions that I had about running the simulation tools. Completing a Ph.D. while working full time is quite a strenuous undertaking and I have been lucky to have understanding managers like Gwen Bernstrom and Michael Scriber as well as technical leads like Paul Messer to help smoothen the path. Above all, I would like to acknowledge the tremendous impact that my parents Anthony and Virginia Rodrigues and my sister Lorraine have had on my life in general. I have fond memories of sitting on my dad’s knees as he helped me memorise the multiplication tables. My mum has been a guiding light and an inspiration to me throughout my entire life. I remember practising addition and subtraction on example sums that she had painstakingly typed out on sheets of paper, as I got ready to give the entrance test to the first grade at St. Vincent’s High School. When we were growing up, my caring sister Lorraine warmed up lunch for me many times, after I had become so v engrossed in my school work that I allowed the food to get cold. My grand-aunt ‘Fat- Mama’ cared for me and nurtured me during my early years and I will always feel her loving presence in my life. And so to all of you who have contributed in some measure towards this achievement, I express my heartfelt thanks. Even the word impossible says “I’m possible” vi Adaptive CORDIC: Using Parallel Angle Recoding to Accelerate CORDIC Rotations. Publication No._____________ Terence Keith Rodrigues, Ph.D. The University of Texas at Austin, 2007 Supervisor: Earl E. Swartzlander, Jr. This dissertation presents the Parallel Angle Recoding algorithm which is used to accelerate the calculation of CORDIC rotations. The CORDIC algorithm is used in the evaluation of a wide variety of elementary functions such as Sin, Cos, Tan, Log, Exp, etc. It is a simple and versatile algorithm, but its characteristic linear convergence causes it to suffer from long latency. It can be sped up by using the angle recoding algorithm which skips over certain intermediate CORDIC iterations to deliver the same precision while requiring 50% or fewer iterations. However because the selection of the angle constants is quite complex and must be performed off-line, its use has been limited to applications where the rotation angle is static and known a priori . This dissertation extends the low-latency advantage of the angle recoding method to dynamic situations too, where the incoming angle of rotation is allowed to take on any arbitrary value. The proposed method is called Parallel Angle Recoding and it makes use of a much simpler angle selection scheme to identify the angle constants needed by angle recoding. Because of its simplicity, it can be easily implemented in hardware without vii having to increase the cycle time. All the angle constants for angle recoding can be found in parallel in a single preliminary step by testing just the initial incoming rotation angle using range comparators – there is no need to perform successive CORDIC iterations in order to identify them. With increasing precision, (N= 8, 16, 24, 32, etc.) the number of comparators which are needed by this scheme increases rapidly. The parallel angle recoding method can be re-formulated to apply to smaller groups of consecutive angle constants known as ‘sections.’ This limits the number of comparators that are needed, to a reasonable amount. There is an attendant savings in area and power consumption, but at the same time the evaluation of multiple sections introduces additional overhead cycles which reduces some of the gains made in latency by the Parallel Angle Recoding method. By interleaving multiple rotations and making use of a small buffer to store intermediate results, the number of overhead cycles can be reduced drastically. The Parallel Angle Recoding technique is modelled using Verilog, synthesised and mapped to a 65 nm. cell library. The latency and area characteristics that are obtained show that the method can improve the performance of the rotation mode in CORDIC, by delivering a reduced iteration count with no increase in the cycle time, and only a modest increase in power and area. viii TABLE OF CONTENTS List of Tables ........................................................................................................ xii List of Figures...................................................................................................... xiv CHAPTER 1 INTRODUCTION 1 1.1 Elementary Functions And Their Applications .....................................1 1.2 Hardware Requirements for Evaluating Elementary Functions ............1 1.3 Classes of algorithms for Evaluating Elementary Functions.................3 1.3.1 Table – Lookup Method................................................................3 1.3.2 Polynomial Approximation:..........................................................4 1.3.3 Rational Approximations..............................................................5 1.3.4 CORDIC Method:.........................................................................6 1.3.5 Quadratic Convergence:................................................................7 1.4 Contribution of this dissertation: ...........................................................7 CHAPTER 2 ORIGINAL CORDIC 10 2.1 Origins of CORDIC .............................................................................10 2.2 Modern Applications of CORDIC.......................................................10 2.2.1 Robotics ......................................................................................11 2.2.2 3-D Computer Graphics..............................................................11 2.2.3 OFDM.........................................................................................12 2.2.4 DCT Compression ......................................................................12 2.3 Original Cordic - Rotation of a vector in a plane.................................13 2.4 Mathematical Formulation Of the Cordic Iterations............................15 CHAPTER 3 PRIOR WORK 19 3.1 A broad survey of Prior Work .............................................................19 3.2 Unified CORDIC .................................................................................21 3.2.1 Iterative Equations ......................................................................22 3.2.2 Convergence of Unified CORDIC in the Rotation Mode...........24 ix 3.3 Control Cordic .....................................................................................26 3.4 Adaptive Cordic using the Static Angle Recoding Algorithm.............29 CHAPTER 4 PARALLEL ANGLE RECODING 32 4.1 Direct Implementation of Angle Recoding In Hardware.....................32 4.2 Dynamic Angle-Constant Selection using Parallel Angle Recoding...34 4.3 Determining the Boundaries of the Contiguous Ranges......................36 CHAPTER 5 IMPROVEMENTS TO PARALLEL ANGLE RECODING 42 5.1 Using Sections to limiting the number of Range Comparators ...........42 5.2 The Effect of using Sections on the Latency .......................................45 5.3 Improving the performance of sections ...............................................49 5.3.1 Advancing the first section of the following rotation angle. ......49 5.3.2 Injecting Sections from Independent Rotation Angles into the Pipeline. ......................................................................................52 CHAPTER 6 MISCELLANEOUS 57 6.1 Scaling Factor K ..................................................................................57 6.2 Performing sign detection with comparators .......................................59 CHAPTER 7 RESULTS 63 7.1 Algorithms being evaluated .................................................................63 7.2 Obtaining the different metrics ............................................................64
Load more

Recommended publications
  • Pipelining and Vector Processing
    Chapter 8 Pipelining and Vector Processing 8–1 If the pipeline stages are heterogeneous, the slowest stage determines the flow rate of the entire pipeline. This leads to other stages idling. 8–2 Pipeline stalls can be caused by three types of hazards: resource, data, and control hazards. Re- source hazards result when two or more instructions in the pipeline want to use the same resource. Such resource conflicts can result in serialized execution, reducing the scope for overlapped exe- cution. Data hazards are caused by data dependencies among the instructions in the pipeline. As a simple example, suppose that the result produced by instruction I1 is needed as an input to instruction I2. We have to stall the pipeline until I1 has written the result so that I2 reads the correct input. If the pipeline is not designed properly, data hazards can produce wrong results by using incorrect operands. Therefore, we have to worry about the correctness first. Control hazards are caused by control dependencies. As an example, consider the flow control altered by a branch instruction. If the branch is not taken, we can proceed with the instructions in the pipeline. But, if the branch is taken, we have to throw away all the instructions that are in the pipeline and fill the pipeline with instructions at the branch target. 8–3 Prefetching is a technique used to handle resource conflicts. Pipelining typically uses just-in- time mechanism so that only a simple buffer is needed between the stages. We can minimize the performance impact if we relax this constraint by allowing a queue instead of a single buffer.
    [Show full text]
  • Diploma Thesis
    Faculty of Computer Science Chair for Real Time Systems Diploma Thesis Timing Analysis in Software Development Author: Martin Däumler Supervisors: Jun.-Prof. Dr.-Ing. Robert Baumgartl Dr.-Ing. Andreas Zagler Date of Submission: March 31, 2008 Martin Däumler Timing Analysis in Software Development Diploma Thesis, Chemnitz University of Technology, 2008 Abstract Rapid development processes and higher customer requirements lead to increasing inte- gration of software solutions in the automotive industry’s products. Today, several elec- tronic control units communicate by bus systems like CAN and provide computation of complex algorithms. This increasingly requires a controlled timing behavior. The following diploma thesis investigates how the timing analysis tool SymTA/S can be used in the software development process of the ZF Friedrichshafen AG. Within the scope of several scenarios, the benefits of using it, the difficulties in using it and the questions that can not be answered by the timing analysis tool are examined. Contents List of Figures iv List of Tables vi 1 Introduction 1 2 Execution Time Analysis 3 2.1 Preface . 3 2.2 Dynamic WCET Analysis . 4 2.2.1 Methods . 4 2.2.2 Problems . 4 2.3 Static WCET Analysis . 6 2.3.1 Methods . 6 2.3.2 Problems . 7 2.4 Hybrid WCET Analysis . 9 2.5 Survey of Tools: State of the Art . 9 2.5.1 aiT . 9 2.5.2 Bound-T . 11 2.5.3 Chronos . 12 2.5.4 MTime . 13 2.5.5 Tessy . 14 2.5.6 Further Tools . 15 2.6 Examination of Methods . 16 2.6.1 Software Description .
    [Show full text]
  • How Data Hazards Can Be Removed Effectively
    International Journal of Scientific & Engineering Research, Volume 7, Issue 9, September-2016 116 ISSN 2229-5518 How Data Hazards can be removed effectively Muhammad Zeeshan, Saadia Anayat, Rabia and Nabila Rehman Abstract—For fast Processing of instructions in computer architecture, the most frequently used technique is Pipelining technique, the Pipelining is consider an important implementation technique used in computer hardware for multi-processing of instructions. Although multiple instructions can be executed at the same time with the help of pipelining, but sometimes multi-processing create a critical situation that altered the normal CPU executions in expected way, sometime it may cause processing delay and produce incorrect computational results than expected. This situation is known as hazard. Pipelining processing increase the processing speed of the CPU but these Hazards that accrue due to multi-processing may sometime decrease the CPU processing. Hazards can be needed to handle properly at the beginning otherwise it causes serious damage to pipelining processing or overall performance of computation can be effected. Data hazard is one from three types of pipeline hazards. It may result in Race condition if we ignore a data hazard, so it is essential to resolve data hazards properly. In this paper, we tries to present some ideas to deal with data hazards are presented i.e. introduce idea how data hazards are harmful for processing and what is the cause of data hazards, why data hazard accord, how we remove data hazards effectively. While pipelining is very useful but there are several complications and serious issue that may occurred related to pipelining i.e.
    [Show full text]
  • Pipelining: Basic Concepts and Approaches
    International Journal of Scientific & Engineering Research, Volume 7, Issue 4, April-2016 1197 ISSN 2229-5518 Pipelining: Basic Concepts and Approaches RICHA BAIJAL1 1Student,M.Tech,Computer Science And Engineering Career Point University,Alaniya,Jhalawar Road,Kota-325003 (Rajasthan) Abstract-This paper is concerned with the pipelining principles while designing a processor.The basics of instruction pipeline are discussed and an approach to minimize a pipeline stall is explained with the help of example.The main idea is to understand the working of a pipeline in a processor.Various hazards that cause pipeline degradation are explained and solutions to minimize them are discussed. Index Terms— Data dependency, Hazards in pipeline, Instruction dependency, parallelism, Pipelining, Processor, Stall. —————————— —————————— 1 INTRODUCTION does the paint. Still,2 rooms are idle. These rooms that I want to paint constitute my hardware.The painter and his skills are the objects and the way i am using them refers to the stag- O understand what pipelining is,let us consider the as- T es.Now,it is quite possible i limit my resources,i.e. I just have sembly line manufacturing of a car.If you have ever gone to a two buckets of paint at a time;therefore,i have to wait until machine work shop ; you might have seen the different as- these two stages give me an output.Although,these are inde- pendent tasks,but what i am limiting is the resources. semblies developed for developing its chasis,adding a part to I hope having this comcept in mind,now the reader
    [Show full text]
  • Powerpc 601 RISC Microprocessor Users Manual
    MPR601UM-01 MPC601UM/AD PowerPC™ 601 RISC Microprocessor User's Manual CONTENTS Paragraph Page Title Number Number About This Book Audience .............................................................................................................. xlii Organization......................................................................................................... xlii Additional Reading ............................................................................................. xliv Conventions ........................................................................................................ xliv Acronyms and Abbreviations ............................................................................. xliv Terminology Conventions ................................................................................. xlvii Chapter 1 Overview 1.1 PowerPC 601 Microprocessor Overview............................................................. 1-1 1.1.1 601 Features..................................................................................................... 1-2 1.1.2 Block Diagram................................................................................................. 1-3 1.1.3 Instruction Unit................................................................................................ 1-5 1.1.3.1 Instruction Queue......................................................................................... 1-5 1.1.4 Independent Execution Units..........................................................................
    [Show full text]
  • Improving UNIX Kernel Performance Using Profile Based Optimization
    Improving UNIX Kernel Performance using Profile Based Optimization Steven E. Speer (Hewlett-Packard) Rajiv Kumar (Hewlett-Packard) and Craig Partridge (Bolt Beranek and Newman/Stanford University) Abstract Several studies have shown that operating system performance has lagged behind improvements in applica- tion performance. In this paper we show how operating systems can be improved to make better use of RISC architectures, particularly in some of the networking code, using a compiling technique known as Profile Based Optimization (PBO). PBO uses profiles from the execution of a program to determine how to best organize the binary code to reduce the number of dynamically taken branches and reduce instruction cache misses. In the case of an operating system, PBO can use profiles produced by instrumented kernels to optimize a kernel image to reflect patterns of use on a particular system. Tests applying PBO to an HP-UX kernel running on an HP9000/720 show that certain parts of the system code (most notably the networking code) achieve substantial performance improvements of up to 35% on micro benchmarks. Overall system performance typically improves by about 5%. 1. Introduction Achieving good operating system performance on a given processor remains a challenge. Operating systems have not experienced the same improvement in transitioning from CISC to RISC processors that has been experi- enced by applications. It is becoming apparent that the differences between RISC and CISC processors have greater significance for operating systems than for applications. (This discovery should, in retrospect, probably not be very surprising. An operating system is far more closely linked to the hardware it runs on than is the average application).
    [Show full text]
  • Analysis of Body Bias Control Using Overhead Conditions for Real Time Systems: a Practical Approach∗
    IEICE TRANS. INF. & SYST., VOL.E101–D, NO.4 APRIL 2018 1116 PAPER Analysis of Body Bias Control Using Overhead Conditions for Real Time Systems: A Practical Approach∗ Carlos Cesar CORTES TORRES†a), Nonmember, Hayate OKUHARA†, Student Member, Nobuyuki YAMASAKI†, Member, and Hideharu AMANO†, Fellow SUMMARY In the past decade, real-time systems (RTSs), which must in RTSs. These techniques can improve energy efficiency; maintain time constraints to avoid catastrophic consequences, have been however, they often require a large amount of power since widely introduced into various embedded systems and Internet of Things they must control the supply voltages of the systems. (IoTs). The RTSs are required to be energy efficient as they are used in embedded devices in which battery life is important. In this study, we in- Body bias (BB) control is another solution that can im- vestigated the RTS energy efficiency by analyzing the ability of body bias prove RTS energy efficiency as it can manage the tradeoff (BB) in providing a satisfying tradeoff between performance and energy. between power leakage and performance without affecting We propose a practical and realistic model that includes the BB energy and the power supply [4], [5].Itseffect is further endorsed when timing overhead in addition to idle region analysis. This study was con- ducted using accurate parameters extracted from a real chip using silicon systems are enabled with silicon on thin box (SOTB) tech- on thin box (SOTB) technology. By using the BB control based on the nology [6], which is a novel and advanced fully depleted sili- proposed model, about 34% energy reduction was achieved.
    [Show full text]
  • Lecture Topics RAW Hazards Stall Penalty
    Lecture Topics ECE 486/586 • Pipelining – Hazards and Stalls • Data Hazards Computer Architecture – Forwarding • Control Hazards Lecture # 11 Reference: • Appendix C: Section C.2 Spring 2015 Portland State University RAW Hazards Stall Penalty Time Clock Cycle 1 2 3 4 5 6 7 8 • If the dependent instruction follows right after the producer Add R2, R3, #100 IF ID EX MEM WB instruction, we need to stall the pipe for 2 cycles (Stall penalty = 2) • What happens if the producer and dependent instructions are Subtract R9, R2, #30 IF IDstall stall EX MEM WB separated by an intermediate instruction? • Subtract is stalled in decode stage for two additional cycles to delay reading Add R2, R3, #100 IF ID EX MEM WB R2 until the new value of R2 has been written by Add How is this pipeline stall implemented in hardware? Or R4, R5, R6 IF ID EX MEM WB • Control circuitry recognizes the data dependency when it decodes Subtract (comparing source register ids with dest. register ids of prior instructions) Subtract R9, R2, #30 IF ID stall EX MEM WB • During cycles 3 to 5: • Add proceeds through the pipe • In this case, stall penalty = 1 • Subtract is held in the ID stage • Stall penalty depends upon the distance between the producer • In cycle 5 and dependent instruction • Add writes R2 in the first half cycle, Subtract reads R2 in the second half cycle Impact of Data Hazards Operand Forwarding - Alleviating Data Hazards • Frequent stalls caused by data hazards can impact the • Stalls due to data dependencies can be mitigated by forwarding • Consider the two instructions discussed in the previous example performance significantly.
    [Show full text]
  • UM0434 E200z3 Powerpc Core Reference Manual
    UM0434 e200z3 PowerPC core Reference manual Introduction The primary objective of this user’s manual is to describe the functionality of the e200z3 embedded microprocessor core for software and hardware developers. This book is intended as a companion to the EREF: A Programmer's Reference Manual for Freescale Book E Processors (hereafter referred to as EREF). Book E is a PowerPC™ architecture definition for embedded processors that ensures binary compatibility with the user-instruction set architecture (UISA) portion of the PowerPC architecture as it was jointly developed by Apple, IBM, and Motorola (referred to as the AIM architecture). This document distinguishes among the three levels of the architectural and implementation definition, as follows: ● The Book E architecture—Book E defines a set of user-level instructions and registers that are drawn from the user instruction set architecture (UISA) portion of the AIM definition PowerPC architecture. Book E also includes numerous supervisor-level registers and instructions as they were defined in the AIM version of the PowerPC architecture for the virtual environment architecture (VEA) and the operating environment architecture (OEA). Because the operating system resources (such as the MMU and interrupts) defined by Book E differ greatly from those defined by the AIM architecture, Book E introduces many new registers and instructions. ● Freescale Book E implementation standards (EIS)—In many cases, the Book E architecture definition provides a general framework, leaving specific details up to the implementation. To ensure consistency among its Book E implementations, Freescale has defined implementation standards that provide an additional layer of architecture between Book E and the actual devices.
    [Show full text]
  • Instruction Pipelining Review
    InstructionInstruction PipeliningPipelining ReviewReview • Instruction pipelining is CPU implementation technique where multiple operations on a number of instructions are overlapped. • An instruction execution pipeline involves a number of steps, where each step completes a part of an instruction. Each step is called a pipeline stage or a pipeline segment. • The stages or steps are connected in a linear fashion: one stage to the next to form the pipeline -- instructions enter at one end and progress through the stages and exit at the other end. • The time to move an instruction one step down the pipeline is is equal to the machine cycle and is determined by the stage with the longest processing delay. • Pipelining increases the CPU instruction throughput: The number of instructions completed per cycle. – Under ideal conditions (no stall cycles), instruction throughput is one instruction per machine cycle, or ideal CPI = 1 • Pipelining does not reduce the execution time of an individual instruction: The time needed to complete all processing steps of an instruction (also called instruction completion latency). – Minimum instruction latency = n cycles, where n is the number of pipeline stages EECC551 - Shaaban (In Appendix A) #1 Lec # 2 Spring 2004 3-10-2004 MIPS In-Order Single-Issue Integer Pipeline Ideal Operation Fill Cycles = number of stages -1 Clock Number Time in clock cycles ® Instruction Number 1 2 3 4 5 6 7 8 9 Instruction I IF ID EX MEM WB Instruction I+1 IF ID EX MEM WB Instruction I+2 IF ID EX MEM WB Instruction I+3 IF ID
    [Show full text]
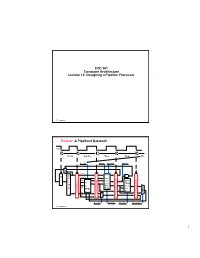
  • ECE 361 Computer Architecture Lecture 13: Designing a Pipeline Processor
    ECE 361 Computer Architecture Lecture 13: Designing a Pipeline Processor 361 hazards.1 Review: A Pipelined Datapath Clk Ifetch Reg/Dec Exec Mem Wr RegWr ExtOp ALUOp Branch 1 0 P PC+4 P C PC+4 C + Imm16 4 M Imm16 E I I x e D F Rs / Zero Data busA m M / / A I E Ra / D e Mem W I x busB m U R R Exec r n Rb RA Do R e e R M 1 i g t Rt g Unit e WA e i i u RFile g s g s x t i t i s e Di e s t r t Rw r Di e Rt e r I 0 r 0 Rd 1 RegDst ALUSrc MemWr MemtoReg 361 hazards.2 1 Review: Pipeline Control “Data Stationary Control” ° The Main Control generates the control signals during Reg/Dec • Control signals for Exec (ExtOp, ALUSrc, ...) are used 1 cycle later • Control signals for Mem (MemWr Branch) are used 2 cycles later • Control signals for Wr (MemtoReg MemWr) are used 3 cycles later Reg/Dec Exec Mem Wr ExtOp ExtOp ALUSrc ALUSrc E M x I I / e D F ALUOp ALUOp M m / / I E e / D Main W m RegDst x RegDst R R Control r R e R e e g MemWr g MemWr MemWr g e i i s g i s s t t i t e s Branch e Branch Branch e r t r r e MemtoReg MemtoReg MemtoReg r MemtoReg RegWr RegWr RegWr RegWr 361 hazards.3 Review: Pipeline Summary ° Pipeline Processor: • Natural enhancement of the multiple clock cycle processor • Each functional unit can only be used once per instruction • If a instruction is going to use a functional unit: - it must use it at the same stage as all other instructions • Pipeline Control: - Each stage’s control signal depends ONLY on the instruction that is currently in that stage 361 hazards.4 2 Outline of Today’s Lecture ° Recap and Introduction ° Introduction
    [Show full text]
  • Pipelined Instruction Executionhazards, Stages
    Computer Architectures Pipelined Instruction Execution Hazards, Stages Balancing, Super-scalar Systems Pavel Píša, Richard Šusta Michal Štepanovský, Miroslav Šnorek Main source of inspiration: Patterson and Hennessy Czech Technical University in Prague, Faculty of Electrical Engineering English version partially supported by: European Social Fund Prague & EU: We invests in your future. B35APO Computer Architectures Ver.1.10 1 Motivation – AMD Bulldozer 15h (FX, Opteron) - 2011 B35APO Computer Architectures 2 Motivation – Intel Nehalem (Core i7) - 2008 B35APO Computer Architectures 3 The Goal of Today Lecture ● Convert/extend CPU presented in the lecture 2 to the pipelined CPU design. ● The following instructions are considered for our CPU design: add, sub, and, or, slt, addi, lw, sw and beq Typ 31… 0 R opcode(6), 31:26 rs(5), 25:21 rt(5), 20:16 rd(5), 15:11 shamt(5) funct(6), 5:0 I opcode(6), 31:26 rs(5), 25:21 rt(5), 20:16 immediate (16), 15:0 J opcode(6), 31:26 address(26), 25:0 B35APO Computer Architectures 4 Single Cycle CPU Together with Memories MemToReg Control MemWrite Unit Branch 31:26 ALUControl 2:0 Opcode ALUScr RegDest 5:0 Funct RegWrite WE3 0 PC’ PC Instr 25:21 SrcA Zero WE A RD A1 RD1 ALU 0 Result 1 A RD 1 20:16 Instr. A2 RD2 0 SrcB AluOut Data ReadData Memory 1 Memory A3 Reg. WD3 File WriteData WD 20:16 Rt 0 WriteReg 1 15:11 Rd + 4 15:0 <<2 Sign Ext SignImm PCBranch + PCPlus4 B35APO Computer Architectures 5 From lecture 2 Single Cycle CPU – Performance: IPS = IC / T = IPCavg.fCLK ● What is the maximal possible frequency of this CPU? ● It is given by latency on the critical path – it is lw in our case: Tc = tPC + tMem + tRFread + tALU + tMem + tMux + tRFsetup WE3 SrcA 0 PC’ PC Instr 25:21 Zero WE A RD A1 RD1 ALU 0 Result 1 A RD 1 20:16 Instr.
    [Show full text]