DOCSLIB.ORG

12 Interval Estimation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
12 Interval Estimation 12 Interval estimation 12.1 Introduction In Chapter 11, we looked into point estimation in the sense of giving single values or points as estimates for well-defined parameters in a pre-selected population den- sity/probability function. If p is the probability that someone contesting an election will win and if we give an estimate as p = 0.7, then we are saying that there is exactly 70% chance of winning. From a layman’s point of view, such an exact number may not be that reasonable. If we say that the chance is between 60 and 75%, it may be more acceptable to a layman. If the waiting time in a queue at a check-out counter in a grocery store is exponentially distributed with expected waiting time θ minutes, time being measured in minutes, and if we give an estimate of θ as between 5 and 10 minutes it may be more reasonable than giving a single number such as the expected waiting time is exactly 6 minutes. If we give an estimate of the expected life-time of individuals in a certain community of people as between 80 and 90 years, it may be more acceptable rather than saying that the expected life time exactly 83 years. Thus, when the unknown parameter θ has a continuous parameter space Ω it may be more reasonable to come up with an interval so that we can say that the unknown parameter θ is somewhere on this interval. We will examine such interval estimation problems here. 12.2 Interval estimation problems In order to explain the various technical terms in this area, it is better to examine a simple problem and then define various terms appearing there, in the light of the il- lustrations. Example 12.1. Let x1,…,xn be iid variables from an exponential population with den- sity 1 f (x, θ)= e−x/θ, x ≥ 0, θ > 0 θ = +⋯+ = u and zero elsewhere. Compute the densities of (1) u x1 xn; (2) v θ and then evaluate a and b such that Pr{a ≤ v ≤ b}=0.95. Solution 12.1. The moment generating function (mgf) of x is known and it is Mx(t)= −1 −n (1−θt) ,1−θt > 0. Since x1,…,xn are iid, the mgf of u = x1 +⋯+xn is Mu(t)=(1−θt) , 1 − θt > 0 or u has a gamma distribution with parameters (α = n, β = θ). The mgf of v is −n available from Mu(t) as Mv(t)=(1−t) ,1−t > 0. In other words, v has a gamma density with the parameters (α = n, β = 1) or it is free of all parameters since n is known. Let the density of v be denoted by g(v). Then all sorts of probability statements can be made Open Access. © 2018 ArakM. Mathai, Hans J. Haubold, published by De Gruyter. This workis licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License. https://doi.org/10.1515/9783110562545-012 356 | 12 Interval estimation on the variable v. Suppose that we wish to find an a such that Pr{v ≤ a} = 0.025 then we have a vn−1 ∫ e−vdv = 0.025. 0 Γ(n) We can either integrate by parts or use incomplete gamma function tables to obtain the exact value of a since n is known. Similarly, we can find a b such that ∞ vn−1 Pr{x ≥ b} = 0.025 ⇒ ∫ e−vdv = 0.025. b Γ(n) This b is also available either integrating by parts or from the incomplete gamma func- tion tables. Then the probability coverage over the interval [a, b] is 0.95 or Pr{a ≤ v ≤ b} = 0.95. We are successful in finding a and b because the distribution of v is free of all pa- rameters. If the density of v contained some parameters, then we could not have found a and b because those points would have been functions of the parameters involved. Hence the success of our procedure depends upon finding a quantity such as v here, which is a function of the sample values x1,…, xn and the parameter (or parameters) under consideration, but whose distribution is free of all parameters. Such quantities are called pivotal quantities. Definition 12.1 (Pivotal quantities). A function of the sample values x1,…, xn and the parameters under consideration but whose distribution is free of all parameters is called a pivotal quantity. Let us examine Example 12.1 once again. We have a probability statement Pr{a ≤ v ≤ b} = 0.95. Let us examine the mathematical inequalities here. (x + ⋯ + x ) a ≤ v ≤ b ⇒ a ≤ 1 n ≤ b θ 1 θ 1 ⇒ ≤ ≤ b (x1 + ⋯ + xn) a (x + ⋯ + x ) (x + ⋯ + x ) ⇒ 1 n ≤ θ ≤ 1 n . b a Since these inequalities are mathematically identical, we must have the probability statements over these intervals identical. That is, (x + ⋯ + x ) (x + ⋯ + x ) (x + ⋯ + x ) Pr{a ≤ 1 n ≤ b} = Pr{ 1 n ≤ θ ≤ 1 n }. (12.1) θ b a Thus, we have converted a probability statement over v into a probability statement over θ. What is the difference between these two probability statements? The first one 12.2 Interval estimation problems | 357 says that the probability that the random variable falls on the fixed interval [a, b] is 0.95. In the second statement, θ is not a random variable but a fixed but unknown parameter and the random variables are at the end points of the interval or here the interval is random, not θ. Hence the probability statement over θ is to be interpreted [ u , u ] . as the probability for the random interval b a covers the unknown θ is 0 95. In this example, we have cut off 0.025 area at the right tail and 0.025 area at the left tail so that the total area cut off is 0.025 + 0.025 = 0.05. If we had cut off an area α 2 each at both the tails then the total area cut off is α and the area in the middle if 1 − α. In our Example 12.1, α = 0.05 and 1 − α = 0.95. We will introduce some standard notations which will come in handy later on. Notation 12.1. Let y be a random variable whose density f (y) is free of all parame- ters. Then we can compute a point b such that from that point onward to the right the area cut off is a specified number, say α. Then this b is usually denoted as yα or the value of y from there onward to the right the area under the density curve or probability function is α or Pr{y ≥ yα} = α. (12.2) Then from Notation 12.1 if a is a point below which of the left tail area is α then the point a should be denoted as y1−α or the point from where onward to the right the area under the curve is 1 − α or the left tail area is α. In Example 12.1 if we wanted to α compute a and b so that equal areas 2 is cut off at the right and left tails, then the first part of equation (12.1) could have been written as Pr{v − α ≤ v ≤ v α } = 1 − α. 1 2 2 Definition 12.2 (Confidence intervals). Let x1,…, xn be a sample from the popula- tion f (x|θ) where θ is the parameter. Suppose that it is possible to construct two functions of the sample values ϕ1(x1,…, xn) and ϕ2(x1,…, xn) so that the probabil- ity for the random interval [ϕ1, ϕ2] covers the unknown parameter θ is 1 − α for a given α. That is, Pr{ϕ1(x1,…, xn) ≤ θ ≤ ϕ2(x1,…, xn)} = 1 − α for all θ in the parameter space Ω. Then 1 − α is called the confidence coefficient, the interval [ϕ1, ϕ2] is called a 100( 1 − α)% confidence interval for θ, ϕ1 is called the lower confidence limit, ϕ2 is called the upper confidence limit and ϕ2 − ϕ1 the length of the confidence interval. When a random interval [ϕ1, ϕ2] is given we are placing 100(1−α)% confidence on our interval saying that this interval will cover the true parameter value θ with proba- bility 1 − α. The meaning is that if we construct the same interval by using samples of 358 | 12 Interval estimation the same size n then in the long run 100(1 − α)% of the intervals will contain the true parameter θ. If one interval is constructed, then that interval need not contain the true parameter θ, the chance that this interval contains the true parameter θ is 1 − α. In our ( +⋯+ ) ( +⋯+ ) Example 12.1, we were placing 95% confidence in the interval [ x1 xn , x1 xn ] to v0.025 v0.975 contain the unknown parameter θ. From Example 12.1 and the discussions above, it is clear that we will be successful in coming up with a 100(1 − α)% confidence interval for a given parameter θ if we have the following: (i) A pivotal quantity Q, that is, a quantity containing the sample values and the pa- rameter θ but whose distribution is free of all parameters. [Note that there may be many pivotal quantities in a given situation.] (ii) Q enables us to convert a probability statement on Q into a mathematically equiv- alent statement on θ. How many such 100(1 − α)% confidence intervals can be constructed for a given θ, if one such interval can be constructed? The answer is: infinitely many.
Load more

Recommended publications
  • Estimating Confidence Regions of Common Measures of (Baseline, Treatment Effect) On
    Estimating confidence regions of common measures of (baseline, treatment effect) on dichotomous outcome of a population Li Yin1 and Xiaoqin Wang2* 1Department of Medical Epidemiology and Biostatistics, Karolinska Institute, Box 281, SE- 171 77, Stockholm, Sweden 2Department of Electronics, Mathematics and Natural Sciences, University of Gävle, SE-801 76, Gävle, Sweden (Email: [email protected]). *Corresponding author Abstract In this article we estimate confidence regions of the common measures of (baseline, treatment effect) in observational studies, where the measure of baseline is baseline risk or baseline odds while the measure of treatment effect is odds ratio, risk difference, risk ratio or attributable fraction, and where confounding is controlled in estimation of both baseline and treatment effect. To avoid high complexity of the normal approximation method and the parametric or non-parametric bootstrap method, we obtain confidence regions for measures of (baseline, treatment effect) by generating approximate distributions of the ML estimates of these measures based on one logistic model. Keywords: baseline measure; effect measure; confidence region; logistic model 1 Introduction Suppose that one conducts a randomized trial to investigate the effect of a dichotomous treatment z on a dichotomous outcome y of certain population, where = 0, 1 indicate the 푧 1 active respective control treatments while = 0, 1 indicate positive respective negative outcomes. With a sufficiently large sample,푦 covariates are essentially unassociated with treatments z and thus are not confounders. Let R = pr( = 1 | ) be the risk of = 1 given 푧 z. Then R is marginal with respect to covariates and thus푦 conditional푧 on treatment푦 z only, so 푧 R is also called marginal risk.
    [Show full text]
  • Theory Pest.Pdf
    Theory for PEST Users Zhulu Lin Dept. of Crop and Soil Sciences University of Georgia, Athens, GA 30602 [email protected] October 19, 2005 Contents 1 Linear Model Theory and Terminology 2 1.1 Amotivationexample ...................... 2 1.2 General linear regression model . 3 1.3 Parameterestimation. 6 1.3.1 Ordinary least squares estimator . 6 1.3.2 Weighted least squares estimator . 7 1.4 Uncertaintyanalysis ....................... 9 1.4.1 Variance-covariance matrix of βˆ and estimation of σ2 . 9 1.4.2 Confidence interval for βj ................ 9 1.4.3 Confidence region for β ................. 10 1.4.4 Confidence interval for E(y0) .............. 10 1.4.5 Prediction interval for a future observation y0 ..... 11 2 Nonlinear regression model 13 2.1 Linearapproximation. 13 2.2 Nonlinear least squares estimator . 14 2.3 Numericalmethods ........................ 14 2.3.1 Steepest Descent algorithm . 16 2.3.2 Gauss-Newton algorithm . 16 2.3.3 Levenberg-Marquardt algorithm . 18 2.3.4 Newton’smethods . 19 1 2.4 Uncertainty analysis . 22 2.4.1 Confidence intervals for parameter and model prediction 22 2.4.2 Nonlinear calibration-constrained method . 23 3 Miscellaneous 27 3.1 Convergence criteria . 27 3.2 Derivatives computation . 28 3.3 Parameter estimation of compartmental models . 28 3.4 Initial values and prior information . 29 3.5 Parametertransformation . 30 1 Linear Model Theory and Terminology Before discussing parameter estimation and uncertainty analysis for nonlin- ear models, we need to review linear model theory as many of the ideas and methods of estimation and analysis (inference) in nonlinear models are essentially linear methods applied to a linear approximate of the nonlinear models.
    [Show full text]
  • Random Vectors
    Random Vectors x is a p×1 random vector with a pdf probability density function f(x): Rp→R. Many books write X for the random vector and X=x for the realization of its value. E[X]= ∫ x f.(x) dx = µ Theorem: E[Ax+b]= AE[x]+b Covariance Matrix E[(x-µ)(x-µ)’]=var(x)=Σ (note the location of transpose) Theorem: Σ=E[xx’]-µµ’ If y is a random variable: covariance C(x,y)= E[(x-µ)(y-ν)’] Theorem: For constants a, A, var (a’x)=a’Σa, var(Ax+b)=AΣA’, C(x,x)=Σ, C(x,y)=C(y,x)’ Theorem: If x, y are independent RVs, then C(x,y)=0, but not conversely. Theorem: Let x,y have same dimension, then var(x+y)=var(x)+var(y)+C(x,y)+C(y,x) Normal Random Vectors The Central Limit Theorem says that if a focal random variable x consists of the sum of many other independent random variables, then the focal random variable will asymptotically have a 2 distribution that is basically of the form e−x , which we call “normal” because it is so common. 2 ⎛ x−µ ⎞ 1 − / 2 −(x−µ) (x−µ) / 2 1 ⎜ ⎟ 1 2 Normal random variable has pdf f (x) = e ⎝ σ ⎠ = e σ 2πσ2 2πσ2 Denote x p×1 normal random variable with pdf 1 −1 f (x) = e−(x−µ)'Σ (x−µ) (2π)p / 2 Σ 1/ 2 where µ is the mean vector and Σ is the covariance matrix: x~Np(µ,Σ).
    [Show full text]
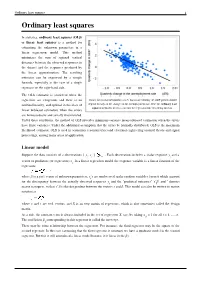
  • Ordinary Least Squares 1 Ordinary Least Squares
    Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β.
    [Show full text]
  • Quantum State Estimation with Nuisance Parameters 2
    Quantum state estimation with nuisance parameters Jun Suzuki E-mail: [email protected] Graduate School of Informatics and Engineering, The University of Electro-Communications, Tokyo, 182-8585 Japan Yuxiang Yang E-mail: [email protected] Institute for Theoretical Physics, ETH Z¨urich, 8093 Z¨urich, Switzerland Masahito Hayashi E-mail: [email protected] Graduate School of Mathematics, Nagoya University, Nagoya, 464-8602, Japan Shenzhen Institute for Quantum Science and Engineering, Southern University of Science and Technology, Shenzhen, 518055, China Center for Quantum Computing, Peng Cheng Laboratory, Shenzhen 518000, China Centre for Quantum Technologies, National University of Singapore, 117542, Singapore Abstract. In parameter estimation, nuisance parameters refer to parameters that are not of interest but nevertheless affect the precision of estimating other parameters of interest. For instance, the strength of noises in a probe can be regarded as a nuisance parameter. Despite its long history in classical statistics, the nuisance parameter problem in quantum estimation remains largely unexplored. The goal of this article is to provide a systematic review of quantum estimation in the presence of nuisance parameters, and to supply those who work in quantum tomography and quantum arXiv:1911.02790v3 [quant-ph] 29 Jun 2020 metrology with tools to tackle relevant problems. After an introduction to the nuisance parameter and quantum estimation theory, we explicitly formulate the problem of quantum state estimation with nuisance parameters. We extend quantum Cram´er-Rao bounds to the nuisance parameter case and provide a parameter orthogonalization tool to separate the nuisance parameters from the parameters of interest. In particular, we put more focus on the case of one-parameter estimation in the presence of nuisance parameters, as it is most frequently encountered in practice.
    [Show full text]
  • Statistical Data Analysis Stat 4: Confidence Intervals, Limits, Discovery
    Statistical Data Analysis Stat 4: confidence intervals, limits, discovery London Postgraduate Lectures on Particle Physics; University of London MSci course PH4515 Glen Cowan Physics Department Royal Holloway, University of London [email protected] www.pp.rhul.ac.uk/~cowan Course web page: www.pp.rhul.ac.uk/~cowan/stat_course.html G. Cowan Statistical Data Analysis / Stat 4 1 Interval estimation — introduction In addition to a ‘point estimate’ of a parameter we should report an interval reflecting its statistical uncertainty. Desirable properties of such an interval may include: communicate objectively the result of the experiment; have a given probability of containing the true parameter; provide information needed to draw conclusions about the parameter possibly incorporating stated prior beliefs. Often use +/- the estimated standard deviation of the estimator. In some cases, however, this is not adequate: estimate near a physical boundary, e.g., an observed event rate consistent with zero. We will look briefly at Frequentist and Bayesian intervals. G. Cowan Statistical Data Analysis / Stat 4 2 Frequentist confidence intervals Consider an estimator for a parameter θ and an estimate We also need for all possible θ its sampling distribution Specify upper and lower tail probabilities, e.g., α = 0.05, β = 0.05, then find functions uα(θ) and vβ(θ) such that: G. Cowan Statistical Data Analysis / Stat 4 3 Confidence interval from the confidence belt The region between uα(θ) and vβ(θ) is called the confidence belt. Find points where observed estimate intersects the confidence belt. This gives the confidence interval [a, b] Confidence level = 1 - α - β = probability for the interval to cover true value of the parameter (holds for any possible true θ).
    [Show full text]
  • Confidence Intervals for Functions of Variance Components Kok-Leong Chiang Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 2000 Confidence intervals for functions of variance components Kok-Leong Chiang Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Statistics and Probability Commons Recommended Citation Chiang, Kok-Leong, "Confidence intervals for functions of variance components " (2000). Retrospective Theses and Dissertations. 13890. https://lib.dr.iastate.edu/rtd/13890 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while ottiers may be f^ any type of computer printer. The quality of this reproduction is dependent upon the quality of ttw copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author dkl not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g.. maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overiaps.
    [Show full text]
  • Monte Carlo Methods for Confidence Bands in Nonlinear Regression Shantonu Mazumdar University of North Florida
    UNF Digital Commons UNF Graduate Theses and Dissertations Student Scholarship 1995 Monte Carlo Methods for Confidence Bands in Nonlinear Regression Shantonu Mazumdar University of North Florida Suggested Citation Mazumdar, Shantonu, "Monte Carlo Methods for Confidence Bands in Nonlinear Regression" (1995). UNF Graduate Theses and Dissertations. 185. https://digitalcommons.unf.edu/etd/185 This Master's Thesis is brought to you for free and open access by the Student Scholarship at UNF Digital Commons. It has been accepted for inclusion in UNF Graduate Theses and Dissertations by an authorized administrator of UNF Digital Commons. For more information, please contact Digital Projects. © 1995 All Rights Reserved Monte Carlo Methods For Confidence Bands in Nonlinear Regression by Shantonu Mazumdar A thesis submitted to the Department of Mathematics and Statistics in partial fulfillment of the requirements for the degree of Master of Science in Mathematical Sciences UNIVERSITY OF NORTH FLORIDA COLLEGE OF ARTS AND SCIENCES May 1995 11 Certificate of Approval The thesis of Shantonu Mazumdar is approved: Signature deleted (Date) ¢)qS- Signature deleted 1./( j ', ().-I' 14I Signature deleted (;;-(-1J' he Depa Signature deleted Chairperson Accepted for the College: Signature deleted Dean Signature deleted ~-3-9£ III Acknowledgment My sincere gratitude goes to Dr. Donna Mohr for her constant encouragement throughout my graduate program, academic assistance and concern for my graduate success. The guidance, support and knowledge that I received from Dr. Mohr while working on this thesis is greatly appreciated. My gratitude is extended to the members of my reviewing committee, Dr. Ping Sa and Dr. Peter Wludyka for their invaluable input into the writing of this thesis.
    [Show full text]
  • Nearly Optimal Tests When a Nuisance Parameter Is Present
    Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis Graham Elliott Ulrich K. Müller Mark W. Watson UCSD Princeton University Princeton University and NBER January 2012 (Revised July 2013) Abstract This paper considers nonstandard hypothesis testing problems that involve a nui- sance parameter. We establish an upper bound on the weighted average power of all valid tests, and develop a numerical algorithm that determines a feasible test with power close to the bound. The approach is illustrated in six applications: inference about a linear regression coe¢ cient when the sign of a control coe¢ cient is known; small sample inference about the di¤erence in means from two independent Gaussian sam- ples from populations with potentially di¤erent variances; inference about the break date in structural break models with moderate break magnitude; predictability tests when the regressor is highly persistent; inference about an interval identi…ed parame- ter; and inference about a linear regression coe¢ cient when the necessity of a control is in doubt. JEL classi…cation: C12; C21; C22 Keywords: Least favorable distribution, composite hypothesis, maximin tests This research was funded in part by NSF grant SES-0751056 (Müller). The paper supersedes the corresponding sections of the previous working papers "Low-Frequency Robust Cointegration Testing" and "Pre and Post Break Parameter Inference" by the same set of authors. We thank Lars Hansen, Andriy Norets, Andres Santos, two referees, the participants of the AMES 2011 meeting at Korea University, of the 2011 Greater New York Metropolitan Econometrics Colloquium, and of a workshop at USC for helpful comments.
    [Show full text]
  • Statistical Inference Using Maximum Likelihood Estimation and the Generalized Likelihood Ratio • When the True Parameter Is on the Boundary of the Parameter Space
    \"( Statistical Inference Using Maximum Likelihood Estimation and the Generalized Likelihood Ratio • When the True Parameter Is on the Boundary of the Parameter Space by Ziding Feng1 and Charles E. McCulloch2 BU-1109-M December 1990 Summary The classic asymptotic properties of the maximum likelihood estimator and generalized likelihood ratio statistic do not hold when the true parameter is on the boundary of the parameter space. An inferential procedure based on an enlarged parameter space is shown to have the classical asymptotic properties. Some other competing procedures are also examined. 1. Introduction • The purpose of this article is to derive an inferential procedure using maximum likelihood estimation and the generalized likelihood ratio statistic under the classic Cramer assumptions but allowing the true parameter value to be on the boundary of the parameter space. The results presented include the existence of a consistent local maxima in the neighborhood of the extended parameter space, the large-sample distribution of this maxima, the large-sample distribution of likelihood ratio statistics based on this maxima, and the construction of the confidence region constructed by what we call the Intersection Method. This method is easy to use and has asymptotically correct coverage probability. We illustrate the technique on a normal mixture problem. 1 Ziding Feng was a graduate student in the Biometrics Unit and Statistics Center, Cornell University. He is now Assistant Member, Fred Hutchinson Cancer Research Center, Seattle, WA 98104. 2 Charles E. McCulloch is an Associate Professor, Biometrics Unit and Statistics Center, Cornell University, Ithaca, NY 14853. • Keyword ,: restricted inference, extended parameter space, asymptotic maximum likelihood.
    [Show full text]
  • Lecture 3. Inference About Multivariate Normal Distribution
    Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X1;:::; Xn be i.i.d. Np(µ, Σ). We are interested in evaluation of the maximum likelihood estimates of µ and Σ. Recall that the joint density of X1 is − 1 1 0 −1 f(x) = j2πΣj 2 exp − (x − µ) Σ (x − µ) ; 2 p n for x 2 R . The negative log likelihood function, given observations x1 = fx1;:::; xng, is then n n 1 X `(µ, Σ j xn) = log jΣj + (x − µ)0Σ−1(x − µ) + c 1 2 2 i i i=1 n n n 1 X = log jΣj + (x¯ − µ)0Σ−1(x¯ − µ) + (x − x¯)0Σ−1(x − x¯): 2 2 2 i i i=1 ~ On this end, denote the centered data matrix by X = [x~1;:::; x~n]p×n, where x~i = xi − x¯. Let n 1 1 X S = X~ X~ 0 = x~ x~0 : 0 n n i i i=1 n Proposition 1. The m.l.e. of µ and Σ, that jointly minimize `(µ, Σ j x1 ), are µ^MLE = x¯; MLE Σb = S0: Note that S0 is a biased estimator of Σ. The sample variance{covariance matrix S = n n−1 S0 is unbiased. For interval estimation of µ, we largely follow Section 7.1 of H¨ardleand Simar (2012). First note that since µ 2 Rp, we need to generalize the notion of intervals (primarily defined for R1) to higher dimension. A simple extension is a direct product of marginal intervals: for intervals a < x < b and c < y < d, we obtain a rectangular region f(x; y) 2 R2 : a < x < b; c < y < dg.
    [Show full text]
  • Composite Hypothesis, Nuisance Parameters’
    Practical Statistics – part II ‘Composite hypothesis, Nuisance Parameters’ W. Verkerke (NIKHEF) Wouter Verkerke, NIKHEF Summary of yesterday, plan for today • Start with basics, gradually build up to complexity of Statistical tests with simple hypotheses for counting data “What do we mean with probabilities” Statistical tests with simple hypotheses for distributions “p-values” “Optimal event selection & Hypothesis testing as basis for event selection machine learning” Composite hypotheses (with parameters) for distributions “Confidence intervals, Maximum Likelihood” Statistical inference with nuisance parameters “Fitting the background” Response functions and subsidiary measurements “Profile Likelihood fits” Introduce concept of composite hypotheses • In most cases in physics, a hypothesis is not “simple”, but “composite” • Composite hypothesis = Any hypothesis which does not specify the population distribution completely • Example: counting experiment with signal and background, that leaves signal expectation unspecified Simple hypothesis ~ s=0 With b=5 s=5 s=10 s=15 Composite hypothesis (My) notation convention: all symbols with ~ are constants Wouter Verkerke, NIKHEF A common convention in the meaning of model parameters • A common convention is to recast signal rate parameters into a normalized form (e.g. w.r.t the Standard Model rate) Simple hypothesis ~ s=0 With b=5 s=5 s=10 s=15 Composite hypothesis ‘Universal’ parameter interpretation makes it easier to work with your models μ=0 no signal Composite hypothesis μ=1 expected signal
    [Show full text]