NOTES Reconsidering Leibniz's Analytic Solution of the Catenary
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

Polar Coordinates, Arc Length and the Lemniscate Curve
Ursinus College Digital Commons @ Ursinus College Transforming Instruction in Undergraduate Calculus Mathematics via Primary Historical Sources (TRIUMPHS) Summer 2018 Gaussian Guesswork: Polar Coordinates, Arc Length and the Lemniscate Curve Janet Heine Barnett Colorado State University-Pueblo, [email protected] Follow this and additional works at: https://digitalcommons.ursinus.edu/triumphs_calculus Click here to let us know how access to this document benefits ou.y Recommended Citation Barnett, Janet Heine, "Gaussian Guesswork: Polar Coordinates, Arc Length and the Lemniscate Curve" (2018). Calculus. 3. https://digitalcommons.ursinus.edu/triumphs_calculus/3 This Course Materials is brought to you for free and open access by the Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) at Digital Commons @ Ursinus College. It has been accepted for inclusion in Calculus by an authorized administrator of Digital Commons @ Ursinus College. For more information, please contact [email protected]. Gaussian Guesswork: Polar Coordinates, Arc Length and the Lemniscate Curve Janet Heine Barnett∗ October 26, 2020 Just prior to his 19th birthday, the mathematical genius Carl Freidrich Gauss (1777{1855) began a \mathematical diary" in which he recorded his mathematical discoveries for nearly 20 years. Among these discoveries is the existence of a beautiful relationship between three particular numbers: • the ratio of the circumference of a circle to its diameter, or π; Z 1 dx • a specific value of a certain (elliptic1) integral, which Gauss denoted2 by $ = 2 p ; and 4 0 1 − x p p • a number called \the arithmetic-geometric mean" of 1 and 2, which he denoted as M( 2; 1). Like many of his discoveries, Gauss uncovered this particular relationship through a combination of the use of analogy and the examination of computational data, a practice that historian Adrian Rice called \Gaussian Guesswork" in his Math Horizons article subtitled \Why 1:19814023473559220744 ::: is such a beautiful number" [Rice, November 2009]. -

The Exponential Function
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 5-2006 The Exponential Function Shawn A. Mousel University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Mousel, Shawn A., "The Exponential Function" (2006). MAT Exam Expository Papers. 26. https://digitalcommons.unl.edu/mathmidexppap/26 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. The Exponential Function Expository Paper Shawn A. Mousel In partial fulfillment of the requirements for the Masters of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor May 2006 Mousel – MAT Expository Paper - 1 One of the basic principles studied in mathematics is the observation of relationships between two connected quantities. A function is this connecting relationship, typically expressed in a formula that describes how one element from the domain is related to exactly one element located in the range (Lial & Miller, 1975). An exponential function is a function with the basic form f (x) = ax , where a (a fixed base that is a real, positive number) is greater than zero and not equal to 1. The exponential function is not to be confused with the polynomial functions, such as x 2. One way to recognize the difference between the two functions is by the name of the function. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Geometric Sequences & Exponential Functions
Algebra I GEOMETRIC SEQUENCES Study Guides Big Picture & EXPONENTIAL FUNCTIONS Both geometric sequences and exponential functions serve as a way to represent the repeated and patterned multiplication of numbers and variables. Exponential functions can be used to represent things seen in the natural world, such as population growth or compound interest in a bank. Key Terms Geometric Sequence: A sequence of numbers in which each number in the sequence is found by multiplying the previous number by a fixed amount called the common ratio. Exponential Function: A function with the form y = A ∙ bx. Geometric Sequences A geometric sequence is a type of pattern where every number in the sequence is multiplied by a certain number called the common ratio. Example: 4, 16, 64, 256, ... Find the common ratio r by dividing each term in the sequence by the term before it. So r = 4 Exponential Functions An exponential function is like a geometric sequence, except geometric sequences are discrete (can only have values at certain points, e.g. 4, 16, 64, 256, ...) and exponential functions are continuous (can take on all possible values). Exponential functions look like y = A ∙ bx, where A is the starting amount and b is like the common ratio of a geometric sequence. Graphing Exponential Functions Here are some examples of exponential functions: Exponential Growth and Decay Growth: y = A ∙ bx when b ≥ 1 Decay: y = A ∙ bx when b is between 0 and 1 your textbook and is for classroom or individual use only. your Disclaimer: this study guide was not created to replace Disclaimer: this study guide was • In exponential growth, the value of y increases (grows) as x increases. -

The Arc Length of a Random Lemniscate
The arc length of a random lemniscate Erik Lundberg, Florida Atlantic University joint work with Koushik Ramachandran [email protected] SEAM 2017 Random lemniscates Topic of my talk last year at SEAM: Random rational lemniscates on the sphere. Topic of my talk today: Random polynomial lemniscates in the plane. Polynomial lemniscates: three guises I Complex Analysis: pre-image of unit circle under polynomial map jp(z)j = 1 I Potential Theory: level set of logarithmic potential log jp(z)j = 0 I Algebraic Geometry: special real-algebraic curve p(x + iy)p(x + iy) − 1 = 0 Polynomial lemniscates: three guises I Complex Analysis: pre-image of unit circle under polynomial map jp(z)j = 1 I Potential Theory: level set of logarithmic potential log jp(z)j = 0 I Algebraic Geometry: special real-algebraic curve p(x + iy)p(x + iy) − 1 = 0 Polynomial lemniscates: three guises I Complex Analysis: pre-image of unit circle under polynomial map jp(z)j = 1 I Potential Theory: level set of logarithmic potential log jp(z)j = 0 I Algebraic Geometry: special real-algebraic curve p(x + iy)p(x + iy) − 1 = 0 Prevalence of lemniscates I Approximation theory: Hilbert's lemniscate theorem I Conformal mapping: Bell representation of n-connected domains I Holomorphic dynamics: Mandelbrot and Julia lemniscates I Numerical analysis: Arnoldi lemniscates I 2-D shapes: proper lemniscates and conformal welding I Harmonic mapping: critical sets of complex harmonic polynomials I Gravitational lensing: critical sets of lensing maps Prevalence of lemniscates I Approximation theory: -

Calculus Formulas and Theorems
Formulas and Theorems for Reference I. Tbigonometric Formulas l. sin2d+c,cis2d:1 sec2d l*cot20:<:sc:20 +.I sin(-d) : -sitt0 t,rs(-//) = t r1sl/ : -tallH 7. sin(A* B) :sitrAcosB*silBcosA 8. : siri A cos B - siu B <:os,;l 9. cos(A+ B) - cos,4cos B - siuA siriB 10. cos(A- B) : cosA cosB + silrA sirrB 11. 2 sirrd t:osd 12. <'os20- coS2(i - siu20 : 2<'os2o - I - 1 - 2sin20 I 13. tan d : <.rft0 (:ost/ I 14. <:ol0 : sirrd tattH 1 15. (:OS I/ 1 16. cscd - ri" 6i /F tl r(. cos[I ^ -el : sitt d \l 18. -01 : COSA 215 216 Formulas and Theorems II. Differentiation Formulas !(r") - trr:"-1 Q,:I' ]tra-fg'+gf' gJ'-,f g' - * (i) ,l' ,I - (tt(.r))9'(.,') ,i;.[tyt.rt) l'' d, \ (sttt rrJ .* ('oqI' .7, tJ, \ . ./ stll lr dr. l('os J { 1a,,,t,:r) - .,' o.t "11'2 1(<,ot.r') - (,.(,2.r' Q:T rl , (sc'c:.r'J: sPl'.r tall 11 ,7, d, - (<:s<t.r,; - (ls(].]'(rot;.r fr("'),t -.'' ,1 - fr(u") o,'ltrc ,l ,, 1 ' tlll ri - (l.t' .f d,^ --: I -iAl'CSllLl'l t!.r' J1 - rz 1(Arcsi' r) : oT Il12 Formulas and Theorems 2I7 III. Integration Formulas 1. ,f "or:artC 2. [\0,-trrlrl *(' .t "r 3. [,' ,t.,: r^x| (' ,I 4. In' a,,: lL , ,' .l 111Q 5. In., a.r: .rhr.r' .r r (' ,l f 6. sirr.r d.r' - ( os.r'-t C ./ 7. /.,,.r' dr : sitr.i'| (' .t 8. tl:r:hr sec,rl+ C or ln Jccrsrl+ C ,f'r^rr f 9. -

Geometric and Arithmetic Postulation of the Exponential Function
J. Austral. Math. Soc. (Series A) 54 (1993), 111-127 GEOMETRIC AND ARITHMETIC POSTULATION OF THE EXPONENTIAL FUNCTION J. PILA (Received 7 June 1991) Communicated by J. H. Loxton Abstract This paper presents new proofs of some classical transcendence theorems. We use real variable methods, and hence obtain only the real variable versions of the theorems we consider: the Hermite-Lindemann theorem, the Gelfond-Schneider theorem, and the Six Exponentials theo- rem. We do not appeal to the Siegel lemma to build auxiliary functions. Instead, the proof employs certain natural determinants formed by evaluating n functions at n points (alter- nants), and two mean value theorems for alternants. The first, due to Polya, gives sufficient conditions for an alternant to be non-vanishing. The second, due to H. A. Schwarz, provides an upper bound. 1991 Mathematics subject classification (Amer. Math. Soc): 11 J 81. 1. Introduction The purpose of this paper is to give new proofs of some classical results in the transcendence theory of the exponential function. We employ some determinantal mean value theorems, and some geometrical properties of the exponential function on the real line. Thus our proofs will yield only the real valued versions of the theorems we consider. Specifically, we give proofs of (the real versions of) the six exponentials theorem, the Gelfond-Schneider theorem, and the Hermite-Lindemann the- orem. We do not use Siegel's lemma on solutions of integral linear equations. Using the data of the hypotheses, we construct certain determinants. With © 1993 Australian Mathematical Society 0263-6115/93 $A2.00 + 0.00 111 Downloaded from https://www.cambridge.org/core. -
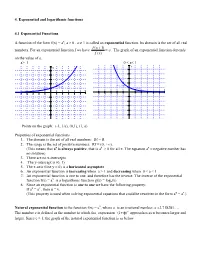
Chapter 4 Notes
4. Exponential and logarithmic functions 4.1 Exponential Functions A function of the form f(x) = ax, a > 0 , a 1 is called an exponential function. Its domain is the set of all real f (x 1) numbers. For an exponential function f we have a . The graph of an exponential function depends f (x) on the value of a. a> 1 0 < a< 1 y y 5 5 4 4 3 3 2 2 (1,a) (-1, 1/a) (-1, 1/a) 1 1 (1,a) x x -5 -4 -3 -2 -1 1 2 3 4 5 -5 -4 -3 -2 -1 1 2 3 4 5 -1 -1 -2 -2 -3 -3 -4 -4 -5 -5 Points on the graph: (-1, 1/a), (0,1), (1, a) Properties of exponential functions 1. The domain is the set of all real numbers: Df = R 2. The range is the set of positive numbers: Rf = (0, +). (This means that ax is always positive, that is ax > 0 for all x. The equation ax = negative number has no solution) 3. There are no x-intercepts 4. The y-intercept is (0, 1) 5. The x-axis (line y = 0) is a horizontal asymptote 6. An exponential function is increasing when a > 1 and decreasing when 0 < a < 1 7. An exponential function is one to one, and therefore has the inverse. The inverse of the exponential x function f(x) = a is a logarithmic function g(x) = loga(x) 8. Since an exponential function is one to one we have the following property: If au = av , then u = v. -

Differentiating Logarithm and Exponential Functions
Differentiating logarithm and exponential functions mc-TY-logexp-2009-1 This unit gives details of how logarithmic functions and exponential functions are differentiated from first principles. In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: • differentiate ln x from first principles • differentiate ex Contents 1. Introduction 2 2. Differentiation of a function f(x) 2 3. Differentiation of f(x)=ln x 3 4. Differentiation of f(x) = ex 4 www.mathcentre.ac.uk 1 c mathcentre 2009 1. Introduction In this unit we explain how to differentiate the functions ln x and ex from first principles. To understand what follows we need to use the result that the exponential constant e is defined 1 1 as the limit as t tends to zero of (1 + t) /t i.e. lim (1 + t) /t. t→0 1 To get a feel for why this is so, we have evaluated the expression (1 + t) /t for a number of decreasing values of t as shown in Table 1. Note that as t gets closer to zero, the value of the expression gets closer to the value of the exponential constant e≈ 2.718.... You should verify some of the values in the Table, and explore what happens as t reduces further. 1 t (1 + t) /t 1 (1+1)1/1 = 2 0.1 (1+0.1)1/0.1 = 2.594 0.01 (1+0.01)1/0.01 = 2.705 0.001 (1.001)1/0.001 = 2.717 0.0001 (1.0001)1/0.0001 = 2.718 We will also make frequent use of the laws of indices and the laws of logarithms, which should be revised if necessary. -

Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time. -

Chapter 8 Logarithms and Exponentials: Logx and E
Chapter 8 Logarithms and Exponentials: log x and ex These two functions are ones with which you already have some familiarity. Both are in- troduced in many high school curricula, as they have widespread applications in both the scientific and financial worlds. In fact, as recently as 50 years ago, many high school math- ematics curricula included considerable study of “Tables of the Logarithm Function” (“log tables”), because this was prior to the invention of the hand-held calculator. During the Great Depression of the 1930’s, many out-of-work mathematicians and scientists were em- ployed as “calculators” or “computers” to develop these tables by hand, laboriously using difference equations, entry by entry! Here, we are going to use our knowledge of the Fun- damental Theorem of Calculus and the Inverse Function Theorem to develop the properties of the Logarithm Function and Exponential Function. Of course, we don’t need tables of these functions any more because it is possible to buy a hand-held electronic calculator for as little as $10.00, which will compute any value of these functions to 10 decimal places or more! 1 2 CHAPTER 8. LOGARITHMS AND EXPONENTIALS: LOG X AND EX 8.1 The Logarithm Function Define log(x) (which we shall be thinking of as the natural logarithm) by the following: Definition 8.1 x 1 log(x)= dt for x>0. 1 t Theorem 8.1 log x is defined for all x>0. It is everywhere differentiable, hence continuous, and is a 1-1 function. The Range of log x is (−∞, ∞).