Lecture 21. Boltzmann Statistics (Ch
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Unit 1 Old Quantum Theory
UNIT 1 OLD QUANTUM THEORY Structure Introduction Objectives li;,:overy of Sub-atomic Particles Earlier Atom Models Light as clectromagnetic Wave Failures of Classical Physics Black Body Radiation '1 Heat Capacity Variation Photoelectric Effect Atomic Spectra Planck's Quantum Theory, Black Body ~diation. and Heat Capacity Variation Einstein's Theory of Photoelectric Effect Bohr Atom Model Calculation of Radius of Orbits Energy of an Electron in an Orbit Atomic Spectra and Bohr's Theory Critical Analysis of Bohr's Theory Refinements in the Atomic Spectra The61-y Summary Terminal Questions Answers 1.1 INTRODUCTION The ideas of classical mechanics developed by Galileo, Kepler and Newton, when applied to atomic and molecular systems were found to be inadequate. Need was felt for a theory to describe, correlate and predict the behaviour of the sub-atomic particles. The quantum theory, proposed by Max Planck and applied by Einstein and Bohr to explain different aspects of behaviour of matter, is an important milestone in the formulation of the modern concept of atom. In this unit, we will study how black body radiation, heat capacity variation, photoelectric effect and atomic spectra of hydrogen can be explained on the basis of theories proposed by Max Planck, Einstein and Bohr. They based their theories on the postulate that all interactions between matter and radiation occur in terms of definite packets of energy, known as quanta. Their ideas, when extended further, led to the evolution of wave mechanics, which shows the dual nature of matter -

Quantum Theory of the Hydrogen Atom
Quantum Theory of the Hydrogen Atom Chemistry 35 Fall 2000 Balmer and the Hydrogen Spectrum n 1885: Johann Balmer, a Swiss schoolteacher, empirically deduced a formula which predicted the wavelengths of emission for Hydrogen: l (in Å) = 3645.6 x n2 for n = 3, 4, 5, 6 n2 -4 •Predicts the wavelengths of the 4 visible emission lines from Hydrogen (which are called the Balmer Series) •Implies that there is some underlying order in the atom that results in this deceptively simple equation. 2 1 The Bohr Atom n 1913: Niels Bohr uses quantum theory to explain the origin of the line spectrum of hydrogen 1. The electron in a hydrogen atom can exist only in discrete orbits 2. The orbits are circular paths about the nucleus at varying radii 3. Each orbit corresponds to a particular energy 4. Orbit energies increase with increasing radii 5. The lowest energy orbit is called the ground state 6. After absorbing energy, the e- jumps to a higher energy orbit (an excited state) 7. When the e- drops down to a lower energy orbit, the energy lost can be given off as a quantum of light 8. The energy of the photon emitted is equal to the difference in energies of the two orbits involved 3 Mohr Bohr n Mathematically, Bohr equated the two forces acting on the orbiting electron: coulombic attraction = centrifugal accelleration 2 2 2 -(Z/4peo)(e /r ) = m(v /r) n Rearranging and making the wild assumption: mvr = n(h/2p) n e- angular momentum can only have certain quantified values in whole multiples of h/2p 4 2 Hydrogen Energy Levels n Based on this model, Bohr arrived at a simple equation to calculate the electron energy levels in hydrogen: 2 En = -RH(1/n ) for n = 1, 2, 3, 4, . -

Vibrational Quantum Number
Fundamentals in Biophotonics Quantum nature of atoms, molecules – matter Aleksandra Radenovic [email protected] EPFL – Ecole Polytechnique Federale de Lausanne Bioengineering Institute IBI 26. 03. 2018. Quantum numbers •The four quantum numbers-are discrete sets of integers or half- integers. –n: Principal quantum number-The first describes the electron shell, or energy level, of an atom –ℓ : Orbital angular momentum quantum number-as the angular quantum number or orbital quantum number) describes the subshell, and gives the magnitude of the orbital angular momentum through the relation Ll2 ( 1) –mℓ:Magnetic (azimuthal) quantum number (refers, to the direction of the angular momentum vector. The magnetic quantum number m does not affect the electron's energy, but it does affect the probability cloud)- magnetic quantum number determines the energy shift of an atomic orbital due to an external magnetic field-Zeeman effect -s spin- intrinsic angular momentum Spin "up" and "down" allows two electrons for each set of spatial quantum numbers. The restrictions for the quantum numbers: – n = 1, 2, 3, 4, . – ℓ = 0, 1, 2, 3, . , n − 1 – mℓ = − ℓ, − ℓ + 1, . , 0, 1, . , ℓ − 1, ℓ – –Equivalently: n > 0 The energy levels are: ℓ < n |m | ≤ ℓ ℓ E E 0 n n2 Stern-Gerlach experiment If the particles were classical spinning objects, one would expect the distribution of their spin angular momentum vectors to be random and continuous. Each particle would be deflected by a different amount, producing some density distribution on the detector screen. Instead, the particles passing through the Stern–Gerlach apparatus are deflected either up or down by a specific amount. -

Further Quantum Physics
Further Quantum Physics Concepts in quantum physics and the structure of hydrogen and helium atoms Prof Andrew Steane January 18, 2005 2 Contents 1 Introduction 7 1.1 Quantum physics and atoms . 7 1.1.1 The role of classical and quantum mechanics . 9 1.2 Atomic physics—some preliminaries . .... 9 1.2.1 Textbooks...................................... 10 2 The 1-dimensional projectile: an example for revision 11 2.1 Classicaltreatment................................. ..... 11 2.2 Quantum treatment . 13 2.2.1 Mainfeatures..................................... 13 2.2.2 Precise quantum analysis . 13 3 Hydrogen 17 3.1 Some semi-classical estimates . 17 3.2 2-body system: reduced mass . 18 3.2.1 Reduced mass in quantum 2-body problem . 19 3.3 Solution of Schr¨odinger equation for hydrogen . ..... 20 3.3.1 General features of the radial solution . 21 3.3.2 Precisesolution.................................. 21 3.3.3 Meanradius...................................... 25 3.3.4 How to remember hydrogen . 25 3.3.5 Mainpoints.................................... 25 3.3.6 Appendix on series solution of hydrogen equation, off syllabus . 26 3 4 CONTENTS 4 Hydrogen-like systems and spectra 27 4.1 Hydrogen-like systems . 27 4.2 Spectroscopy ........................................ 29 4.2.1 Main points for use of grating spectrograph . ...... 29 4.2.2 Resolution...................................... 30 4.2.3 Usefulness of both emission and absorption methods . 30 4.3 The spectrum for hydrogen . 31 5 Introduction to fine structure and spin 33 5.1 Experimental observation of fine structure . ..... 33 5.2 TheDiracresult ..................................... 34 5.3 Schr¨odinger method to account for fine structure . 35 5.4 Physical nature of orbital and spin angular momenta . -

The Quantum Mechanical Model of the Atom
The Quantum Mechanical Model of the Atom Quantum Numbers In order to describe the probable location of electrons, they are assigned four numbers called quantum numbers. The quantum numbers of an electron are kind of like the electron’s “address”. No two electrons can be described by the exact same four quantum numbers. This is called The Pauli Exclusion Principle. • Principle quantum number: The principle quantum number describes which orbit the electron is in and therefore how much energy the electron has. - it is symbolized by the letter n. - positive whole numbers are assigned (not including 0): n=1, n=2, n=3 , etc - the higher the number, the further the orbit from the nucleus - the higher the number, the more energy the electron has (this is sort of like Bohr’s energy levels) - the orbits (energy levels) are also called shells • Angular momentum (azimuthal) quantum number: The azimuthal quantum number describes the sublevels (subshells) that occur in each of the levels (shells) described above. - it is symbolized by the letter l - positive whole number values including 0 are assigned: l = 0, l = 1, l = 2, etc. - each number represents the shape of a subshell: l = 0, represents an s subshell l = 1, represents a p subshell l = 2, represents a d subshell l = 3, represents an f subshell - the higher the number, the more complex the shape of the subshell. The picture below shows the shape of the s and p subshells: (notice the electron clouds) • Magnetic quantum number: All of the subshells described above (except s) have more than one orientation. -

4 Nuclear Magnetic Resonance
Chapter 4, page 1 4 Nuclear Magnetic Resonance Pieter Zeeman observed in 1896 the splitting of optical spectral lines in the field of an electromagnet. Since then, the splitting of energy levels proportional to an external magnetic field has been called the "Zeeman effect". The "Zeeman resonance effect" causes magnetic resonances which are classified under radio frequency spectroscopy (rf spectroscopy). In these resonances, the transitions between two branches of a single energy level split in an external magnetic field are measured in the megahertz and gigahertz range. In 1944, Jevgeni Konstantinovitch Savoiski discovered electron paramagnetic resonance. Shortly thereafter in 1945, nuclear magnetic resonance was demonstrated almost simultaneously in Boston by Edward Mills Purcell and in Stanford by Felix Bloch. Nuclear magnetic resonance was sometimes called nuclear induction or paramagnetic nuclear resonance. It is generally abbreviated to NMR. So as not to scare prospective patients in medicine, reference to the "nuclear" character of NMR is dropped and the magnetic resonance based imaging systems (scanner) found in hospitals are simply referred to as "magnetic resonance imaging" (MRI). 4.1 The Nuclear Resonance Effect Many atomic nuclei have spin, characterized by the nuclear spin quantum number I. The absolute value of the spin angular momentum is L =+h II(1). (4.01) The component in the direction of an applied field is Lz = Iz h ≡ m h. (4.02) The external field is usually defined along the z-direction. The magnetic quantum number is symbolized by Iz or m and can have 2I +1 values: Iz ≡ m = −I, −I+1, ..., I−1, I. -

Quantum Mechanics C (Physics 130C) Winter 2015 Assignment 2
University of California at San Diego { Department of Physics { Prof. John McGreevy Quantum Mechanics C (Physics 130C) Winter 2015 Assignment 2 Posted January 14, 2015 Due 11am Thursday, January 22, 2015 Please remember to put your name at the top of your homework. Go look at the Physics 130C web site; there might be something new and interesting there. Reading: Preskill's Quantum Information Notes, Chapter 2.1, 2.2. 1. More linear algebra exercises. (a) Show that an operator with matrix representation 1 1 1 P = 2 1 1 is a projector. (b) Show that a projector with no kernel is the identity operator. 2. Complete sets of commuting operators. In the orthonormal basis fjnign=1;2;3, the Hermitian operators A^ and B^ are represented by the matrices A and B: 0a 0 0 1 0 0 ib 01 A = @0 a 0 A ;B = @−ib 0 0A ; 0 0 −a 0 0 b with a; b real. (a) Determine the eigenvalues of B^. Indicate whether its spectrum is degenerate or not. (b) Check that A and B commute. Use this to show that A^ and B^ do so also. (c) Find an orthonormal basis of eigenvectors common to A and B (and thus to A^ and B^) and specify the eigenvalues for each eigenvector. (d) Which of the following six sets form a complete set of commuting operators for this Hilbert space? (Recall that a complete set of commuting operators allow us to specify an orthonormal basis by their eigenvalues.) fA^g; fB^g; fA;^ B^g; fA^2; B^g; fA;^ B^2g; fA^2; B^2g: 1 3.A positive operator is one whose eigenvalues are all positive. -
![On the Symmetry of the Quantum-Mechanical Particle in a Cubic Box Arxiv:1310.5136 [Quant-Ph] [9] Hern´Andez-Castillo a O and Lemus R 2013 J](https://docslib.b-cdn.net/cover/3436/on-the-symmetry-of-the-quantum-mechanical-particle-in-a-cubic-box-arxiv-1310-5136-quant-ph-9-hern%C2%B4andez-castillo-a-o-and-lemus-r-2013-j-563436.webp)
On the Symmetry of the Quantum-Mechanical Particle in a Cubic Box Arxiv:1310.5136 [Quant-Ph] [9] Hern´Andez-Castillo a O and Lemus R 2013 J
On the symmetry of the quantum-mechanical particle in a cubic box Francisco M. Fern´andez INIFTA (UNLP, CCT La Plata-CONICET), Blvd. 113 y 64 S/N, Sucursal 4, Casilla de Correo 16, 1900 La Plata, Argentina E-mail: [email protected] arXiv:1310.5136v2 [quant-ph] 25 Dec 2014 Particle in a cubic box 2 Abstract. In this paper we show that the point-group (geometrical) symmetry is insufficient to account for the degeneracy of the energy levels of the particle in a cubic box. The discrepancy is due to hidden (dynamical symmetry). We obtain the operators that commute with the Hamiltonian one and connect eigenfunctions of different symmetries. We also show that the addition of a suitable potential inside the box breaks the dynamical symmetry but preserves the geometrical one.The resulting degeneracy is that predicted by point-group symmetry. 1. Introduction The particle in a one-dimensional box with impenetrable walls is one of the first models discussed in most introductory books on quantum mechanics and quantum chemistry [1, 2]. It is suitable for showing how energy quantization appears as a result of certain boundary conditions. Once we have the eigenvalues and eigenfunctions for this model one can proceed to two-dimensional boxes and discuss the conditions that render the Schr¨odinger equation separable [1]. The particular case of a square box is suitable for discussing the concept of degeneracy [1]. The next step is the discussion of a particle in a three-dimensional box and in particular the cubic box as a representative of a quantum-mechanical model with high symmetry [2]. -

A Relativistic Electron in a Coulomb Potential
A Relativistic Electron in a Coulomb Potential Alfred Whitehead Physics 518, Fall 2009 The Problem Solve the Dirac Equation for an electron in a Coulomb potential. Identify the conserved quantum numbers. Specify the degeneracies. Compare with solutions of the Schrödinger equation including relativistic and spin corrections. Approach My approach follows that taken by Dirac in [1] closely. A few modifications taken from [2] and [3] are included, particularly in regards to the final quantum numbers chosen. The general strategy is to first find a set of transformations which turn the Hamiltonian for the system into a form that depends only on the radial variables r and pr. Once this form is found, I solve it to find the energy eigenvalues and then discuss the energy spectrum. The Radial Dirac Equation We begin with the electromagnetic Hamiltonian q H = p − cρ ~σ · ~p − A~ + ρ mc2 (1) 0 1 c 3 with 2 0 0 1 0 3 6 0 0 0 1 7 ρ1 = 6 7 (2) 4 1 0 0 0 5 0 1 0 0 2 1 0 0 0 3 6 0 1 0 0 7 ρ3 = 6 7 (3) 4 0 0 −1 0 5 0 0 0 −1 1 2 0 1 0 0 3 2 0 −i 0 0 3 2 1 0 0 0 3 6 1 0 0 0 7 6 i 0 0 0 7 6 0 −1 0 0 7 ~σ = 6 7 ; 6 7 ; 6 7 (4) 4 0 0 0 1 5 4 0 0 0 −i 5 4 0 0 1 0 5 0 0 1 0 0 0 i 0 0 0 0 −1 We note that, for the Coulomb potential, we can set (using cgs units): Ze2 p = −eΦ = − o r A~ = 0 This leads us to this form for the Hamiltonian: −Ze2 H = − − cρ ~σ · ~p + ρ mc2 (5) r 1 3 We need to get equation 5 into a form which depends not on ~p, but only on the radial variables r and pr. -
Constructing Non-Linear Quantum Electronic Circuits Circuit Elements: Anharmonic Oscillator: Non-Linear Energy Level Spectrum
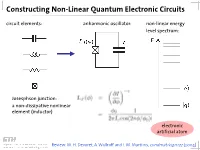
Constructing Non-Linear Quantum Electronic Circuits circuit elements: anharmonic oscillator: non-linear energy level spectrum: Josesphson junction: a non-dissipative nonlinear element (inductor) electronic artificial atom Review: M. H. Devoret, A. Wallraff and J. M. Martinis, condmat/0411172 (2004) A Classification of Josephson Junction Based Qubits How to make use in of Jospehson junctions in a qubit? Common options of bias (control) circuits: phase qubit charge qubit flux qubit (Cooper Pair Box, Transmon) current bias charge bias flux bias How is the control circuit important? The Cooper Pair Box Qubit A Charge Qubit: The Cooper Pair Box discrete charge on island: continuous gate charge: total box capacitance Hamiltonian: electrostatic part: charging energy magnetic part: Josephson energy Hamilton Operator of the Cooper Pair Box Hamiltonian: commutation relation: charge number operator: eigenvalues, eigenfunctions completeness orthogonality phase basis: basis transformation Solving the Cooper Pair Box Hamiltonian Hamilton operator in the charge basis N : solutions in the charge basis: Hamilton operator in the phase basis δ : transformation of the number operator: solutions in the phase basis: Energy Levels energy level diagram for EJ=0: • energy bands are formed • bands are periodic in Ng energy bands for finite EJ • Josephson coupling lifts degeneracy • EJ scales level separation at charge degeneracy Charge and Phase Wave Functions (EJ << EC) courtesy CEA Saclay Charge and Phase Wave Functions (EJ ~ EC) courtesy CEA Saclay Tuning the Josephson Energy split Cooper pair box in perpendicular field = ( ) , cos cos 2 � � − − ̂ 0 SQUID modulation of Josephson energy consider two state approximation J. Clarke, Proc. IEEE 77, 1208 (1989) Two-State Approximation Restricting to a two-charge Hilbert space: Shnirman et al., Phys. -

1 Does Consciousness Really Collapse the Wave Function?
Does consciousness really collapse the wave function?: A possible objective biophysical resolution of the measurement problem Fred H. Thaheld* 99 Cable Circle #20 Folsom, Calif. 95630 USA Abstract An analysis has been performed of the theories and postulates advanced by von Neumann, London and Bauer, and Wigner, concerning the role that consciousness might play in the collapse of the wave function, which has become known as the measurement problem. This reveals that an error may have been made by them in the area of biology and its interface with quantum mechanics when they called for the reduction of any superposition states in the brain through the mind or consciousness. Many years later Wigner changed his mind to reflect a simpler and more realistic objective position, expanded upon by Shimony, which appears to offer a way to resolve this issue. The argument is therefore made that the wave function of any superposed photon state or states is always objectively changed within the complex architecture of the eye in a continuous linear process initially for most of the superposed photons, followed by a discontinuous nonlinear collapse process later for any remaining superposed photons, thereby guaranteeing that only final, measured information is presented to the brain, mind or consciousness. An experiment to be conducted in the near future may enable us to simultaneously resolve the measurement problem and also determine if the linear nature of quantum mechanics is violated by the perceptual process. Keywords: Consciousness; Euglena; Linear; Measurement problem; Nonlinear; Objective; Retina; Rhodopsin molecule; Subjective; Wave function collapse. * e-mail address: [email protected] 1 1. -

Molecular Energy Levels
MOLECULAR ENERGY LEVELS DR IMRANA ASHRAF OUTLINE q MOLECULE q MOLECULAR ORBITAL THEORY q MOLECULAR TRANSITIONS q INTERACTION OF RADIATION WITH MATTER q TYPES OF MOLECULAR ENERGY LEVELS q MOLECULE q In nature there exist 92 different elements that correspond to stable atoms. q These atoms can form larger entities- called molecules. q The number of atoms in a molecule vary from two - as in N2 - to many thousand as in DNA, protiens etc. q Molecules form when the total energy of the electrons is lower in the molecule than in individual atoms. q The reason comes from the Aufbau principle - to put electrons into the lowest energy configuration in atoms. q The same principle goes for molecules. q MOLECULE q Properties of molecules depend on: § The specific kind of atoms they are composed of. § The spatial structure of the molecules - the way in which the atoms are arranged within the molecule. § The binding energy of atoms or atomic groups in the molecule. TYPES OF MOLECULES q MONOATOMIC MOLECULES § The elements that do not have tendency to form molecules. § Elements which are stable single atom molecules are the noble gases : helium, neon, argon, krypton, xenon and radon. q DIATOMIC MOLECULES § Diatomic molecules are composed of only two atoms - of the same or different elements. § Examples: hydrogen (H2), oxygen (O2), carbon monoxide (CO), nitric oxide (NO) q POLYATOMIC MOLECULES § Polyatomic molecules consist of a stable system comprising three or more atoms. TYPES OF MOLECULES q Empirical, Molecular And Structural Formulas q Empirical formula: Indicates the simplest whole number ratio of all the atoms in a molecule.