Ab Initio Modelling of Photoinduced Electron Dynamics in Nanostructures
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

会议详细议程(Final Program)
会议详细议程(Final Program) 2019 International Conference on Display Technology March 26th—29th, 2019 (Tuesday - Friday) Kunshan International Convention and Exhibition Center Kunshan, Suzhou, China Plenary Session Wednesday, Mar. 27/14:00—18:00/Reception Hall Chair: Shintson Wu (吴诗聪), University of Central Florida (UCF) Title: Laser display Technology (14:00-14:30) Zuyan Xu (许祖彦), Technical Institute of Physics and Chemistry, China Academy of Engineering (CAE) Title: Thin film transistor technology and applications (14:30-15:00) Ming Liu (刘明), Institute of Microelectronics of the Chinese Academy of Sciences Title: Technology creates a win-win future (15:00-15:30) Wenbao Gao (高文宝), BOE Title: Gallium nitride micro-LEDs: a novel multi-mode, high-brightness and fast-response display technology (15:30-16:00) Martin Dawson, the University of Strathclyde’s Institute of Photonics, the Fraunhofer Centre for Applied Photonics Title: Virtual and Augmented Reality: Hope or Hype? (16:00-16:30) Achin Bhowmik, Starkey Hearing Technologies Title: Monocular Vision Impact: Monocular 3D and AR Display and Depth Detection with Monocular Camera (16:30-17:00) Haruhiko Okumura, Media AI Lab, Toshiba Title: ePaper, The Most Suitable Display Technology in AIoT (17:00-17:30) Fu-Jen (Frank) Ko, E Ink Holdings Inc. Title: Application Advantage of Laser Display in TV Market and Progress of Hisense (17:30- 18:00) Weidong Liu (刘卫东), Hisense Thursday, Mar. 28/8:30—12:30/Reception Hall Chair: Hoi S. Kwok (郭海成), Hong Kong University of Science and Technology Title: High Performance Tungsten-TADF OLED Emitters (8:30-9:00) Chi-Ming CHE (支志明), The University of Hong Kong Title: Challenges of TFT Technology for AMOLED Display (9:00-9:30) Junfeng Li (李俊峰), Nanyang Technological University, Innovation Research Institute of Visionox Technology Co., Ltd. -

Feature Article: Will Quantum Dots Make for a Brighter Future?
Renishaw plc T +44 (0)1453 524524 New Mills, Wotton-under-Edge, F +44 (0)1453 524901 Gloucestershire, GL12 8JR E [email protected] United Kingdom www.renishaw.com Feature article Will quantum dots make for a brighter future? First discovered in 1980, colloidal semiconductor lighting component market will surpass US$ 2 billion by the nanocrystals or quantum dots (QDs) are typically between end of 2016 and reach US$ 10.6 billion by 2025. 2 - 10 nanometres (nm) in diameter and are now being QD-backlit LCDs and QLEDs commercialised with possible applications in a variety of thin film devices including solar cells, photodetectors and The most immediate applications for QDs are in LCD LEDs. QDs have profound implications for the flat panel backlighting applications (LED TVs). QDs have been display (FPD) industry, but is it really a case of all change incorporated into a filter film designed to be inter-leaved from here on in? between the LED backlight unit and LCD panel. Current LCD backlights use white LEDs, which are blue LEDs coated with a One of the many advantages of QDs is their colour tunability phosphor layer - making them rather inefficient. The quantum resulting from a quantum mechanical effect known as dot filter allows the use of pure blue LEDs in the backlight as ‘confinement’. Quantum dots are also both photo- and it converts some of the incident blue light, by absorption and electro-luminescent as a result of their material composition, re-emission, into very pure green and red. As a result, the LCD which may include Cadmium Selenide (CdSe) and Zinc panel receives a richer white light which expands the range Sulphide (ZnS). -

Quantum Dots for Wide Color Gamut Displays from Photoluminescence
Kang et al. Nanoscale Research Letters (2017) 12:154 DOI 10.1186/s11671-017-1907-1 NANO EXPRESS Open Access Quantum Dots for Wide Color Gamut Displays from Photoluminescence to Electroluminescence Yongyin Kang1, Zhicheng Song2*, Xiaofang Jiang1, Xia Yin1, Long Fang1, Jing Gao1, Yehua Su1 and Fei Zhao1* Abstract Monodisperse quantum dots (QDs) were prepared by low-temperature process. The remarkable narrow emission peak of the QDs helps the liquid crystal displays (LCD) and electroluminescence displays (QD light-emitting diode, QLED) to generate wide color gamut performance. The range of the color gamut for QD light-converting device (QLCD) is controlled by both the QDs and color filters (CFs) in LCD, and for QLED, the optimized color gamut is dominated by QD materials. Keywords: Quantum dots (QDs), Quantum dot light-converting device (QLCD), Color filter (CF), Quantum dot light-emitting diode (QLED), Wide color gamut, Solution process Background ways to produce white light using LEDs, and the color Colloidal quantum dots (QDs) have been actively pursued gamut is determined by the contour of the emission for both fundamental research and industrial development peak from the phosphors. The conventional method uses due to their solution processibility and size-dependent a blue LED chip with YAG (yttrium-aluminum-garnet)- optical properties associated with quantum confinement based phosphor directly packaged on its top, the color [1–4]. The most promising application of QDs is as emit- gamut is typically ~72% NTSC (National Television ters in biomedical labeling, solid-state lighting, and display Standards Committee). Advanced phosphor-based tech- [5–7]. For instance, in 2009, the US Department of Energy nologies replace the YAG by green phosphors and the (DOE) highlighted a high-performance solid-state lighting red phosphors, namely RG phosphor solution. -

Download the Entire Issue in PDF Format Here
Mar-Apr Cover_SID Cover 3/15/2015 4:57 PM Page 1 DISPLAY WEEK PREVIEW / TOPICS IN APPLIED VISION Mar./Apr. 2015 Official Monthly Publication of the Society for Information Display • www.informationdisplay.org Vol. 31, No. 2 Test Solutions for Perfect Display Quality New Name. Still Radiant. Radiant Zemax is now Radiant Vision Systems! The name is new, but our commitment to delivering advanced display test solutions remains unchanged. The world’s leading makers of display devices rely on Radiant’s automated visual inspection systems to measure uniformity, chromaticity, and detect Mura and other defects throughout the manufacturing process. Visit our all new website, www.RadiantVisionSystems.com to learn how our integrated test solutions can help you improve supply chain performance, reduce production costs, and ensure a customer experience that is nothing less than Radiant. Visit us at booth 834 Radiant Vision Systems, LLC Global Headquarters - Redmond, WA USA | +1 425 844-0152 | www.RadiantVisionSystems.com | [email protected] ID TOC Issue2 p1_Layout 1 3/18/2015 6:31 PM Page 1 SOCIETY FOR INFORMATION DISPLAY Information SID MARCH/APRIL 2015 DISPLAY VOL. 31, NO. 2 ON THE COVER: This year’s winners of the Society for Information Display’s Honors and Awards include Dr. Junji Kido, who will receive the Karl Ferdinand Braun Prize; Dr. Shohei contents Naemura, who will receive the Jan Rajchman 2 Editorial: The Pace of Innovation Prize; Dr. Ingrid Heynderickx, who will be awardedMar-Apr Cover_SID Coverthe 3/15/2015 Otto 4:57 PM Page 1 Schade Prize; Dr. Jin Jang, n By Stephen P. -

Recent Developments in Applications of Quantum-Dot Based Light
DOI: 10.5772/intechopen.69177 Provisional chapter Chapter 2 Recent Developments in Applications of Quantum-Dot RecentBased Light-Emitting Developments Diodes in Applications of Quantum-Dot Based Light-Emitting Diodes Anca Armăşelu Anca Armăşelu Additional information is available at the end of the chapter Additional information is available at the end of the chapter http://dx.doi.org/10.5772/intechopen.69177 Abstract Quantum dot-based light-emitting diodes (QD-LEDs) represent a form of light-emitting technology and are regarded like a next generation of display technology after the organic light-emitting diodes (OLEDs) display. QD-LEDs are different from liquid crystal displays (LCDs), OLEDs, and plasma displays due to the fact that QD-LEDs present an ideal blend of high brightness, efficiency with long lifetime, flexibility, and low-processing cost of organic LEDs. So, QD-LEDs show theoretical performance limits which surpass all other display technologies. The goal of this chapter is, firstly, to provide a historical prospective study of QD-LEDs applications in display and lighting technologies, secondly, to present the most recent improvements in this field, and finally, to discuss about some current directions in QD-LEDs research that concentrate on the realization of the next-generation displays and high-quality lighting with superior color gamut, higher efficiency, and high color rendering index. Keywords: quantum dots, quantum dot-based light-emitting diodes, display technology, lighting technology 1. Introduction Quantum dots (QDs) have attracted interest in the fields of optical applications such as quan- tum computing, biological, and chemical applications. In contradistinction to the traditional fluorophores, QDs have unique optical and electronic features, which comprise high quantum yields, high molar extinction coefficients, large effec- tive Stokes shifts [1, 2], broad excitation profiles, narrow/symmetric emission spectra, high resistance to reactive oxygen-mediated photobleaching [2, 3], and are against metabolic deg- radation [4, 5]. -

Module-4 Unit-5 NSNT Quantum Dots Introduction a Quantum Dot (QD) Is an Extremely Small Particle Whose Properties Can Be Drasti
Module-4_Unit-5_ NSNT Quantum Dots Introduction A quantum dot (QD) is an extremely small particle whose properties can be drastically changed merely by removing or adding an electron. In this parlance, an isolated atom can also be termed as a quantum dot. However, only a cluster of atoms or molecules demonstrates property variations. In biochemistry, QDs are often termed as redox groups. QDs are referred as quantum bits or qubits in nanotechnology. The dimensions of QDs are of the order of few nanometers. Nanotechnology is a multi-disciplinary field wherein the problem often includes studying biology, chemistry, computer science, electronics, etc. For example, consider a hypothetical biochip, which is grown analogous to a tree from a seed, and which might also include a computer inside it. In this analogy, both terms - a qubit or redox group - both are equally applicable. Besides, the classification of this chip as animate or inanimate, is difficult to accomplish. Each QD present in this chip may account for one or more data bits. In some cases, an electron within the QD may occupy several states, thus, a QD may also represent a byte of data, instead of a bit (in case of qubit). Alternately, one QD might be simultaneously involved in more than one computations. In addition to these applications, other sophisticated uses of a QD may include nano-mechanics, neural networks, high density data storage, etc. Applications of Quantum Dots (QDs) a. Solar Cells One of the most important features of silicon of use in electronic devices (e.g. transistors) is doping. Wherein small quantities of various elements can be added to silicon in order to generate either an excess (n-type) or deficiency (p-type) of electrons in it, thereby enhancing the material’s conductivity. -

Micro-Light-Emitting Diodes with Quantum Dots in Display Technology
Liu et al. Light: Science & Applications (2020) 9:83 Official journal of the CIOMP 2047-7538 https://doi.org/10.1038/s41377-020-0268-1 www.nature.com/lsa REVIEW ARTICLE Open Access Micro-light-emitting diodes with quantum dots in display technology Zhaojun Liu1, Chun-Ho Lin 2, Byung-Ryool Hyun1, Chin-Wei Sher3,4, Zhijian Lv1, Bingqing Luo5, Fulong Jiang1, Tom Wu2, Chih-Hsiang Ho6,Hao-ChungKuo4 and Jr-Hau He 7 Abstract Micro-light-emitting diodes (μ-LEDs) are regarded as the cornerstone of next-generation display technology to meet the personalised demands of advanced applications, such as mobile phones, wearable watches, virtual/ augmented reality, micro-projectors and ultrahigh-definition TVs. However, as the LED chip size shrinks to below 20 μm, conventional phosphor colour conversion cannot present sufficient luminance and yield to support high- resolution displays due to the low absorption cross-section. The emergence of quantum dot (QD) materials is expected to fill this gap due to their remarkable photoluminescence, narrow bandwidth emission, colour tuneability, high quantum yield and nanoscale size, providing a powerful full-colour solution for μ-LED displays. Here, we comprehensively review the latest progress concerning the implementation of μ-LEDsandQDsindisplay technology, including μ-LED design and fabrication, large-scale μ-LED transfer and QD full-colour strategy. Outlooks on QD stability, patterning and deposition and challenges of μ-LED displays are also provided. Finally, we discuss the advanced applications of QD-based μ-LED displays, showing the bright future of this technology. 1234567890():,; 1234567890():,; 1234567890():,; 1234567890():,; Introduction microdisk LED with a diameter of ~12 μm1. -

Wed. Nov 27, 2019 Mid-Sized Hall a Image Quality and Measurements
Wed. Nov 27, 2019 Oral Presentation The 26th International Display Workshops (IDW '19) Wed. Nov 27, 2019 [VHF2-2] Effect of External Human Machine Interface Mid-sized Hall A (eHMI) of Automated Vehicle on Pedestrian’ s Recognition Oral Presentation *Naoto Matsunaga1, Tatsuru Daimon1, Naoki Yokota1, [VHF1] Image Quality and Measurements Satoshi Kitazaki2 (1. Keio University (Japan), 2. Chair: Kenichiro Masaoka (NHK) National Institute of Advanced Industrial Science Co-Chair: Keita Hirai (Chiba Univ.) 1:40 PM - 3:10 PM Mid-sized Hall A (1F) and Technology (Japan)) 3:45 PM - 4:05 PM [VHF1-OP] Opening [VHF2-3] Influence of Cabin Vibration on Driver’ s 1:40 PM - 1:45 PM Depth Perception and Subjective Conviction [VHF1-1] A Fundamental Evaluation of Visual Resolution When Using Automotive 3D Head-Up Display - of Displays Considering Different Sub-Pixel Basic Study on the Relationship between Structures Degree of Correction and Driver’ s *Daisuke Nakayama1, Midori Tanaka1, Takahiko Recognition- Horiuchi1 (1. Chiba University (Japan)) *Kazuki Matsuhashi1, Tatsuru Daimon2, Ryo Noguchi1, 1:45 PM - 2:05 PM Ken'ichi Kasazumi3, Toshiya Mori3 (1. Graduate [VHF1-2] Perceptually Optimized Image Enhancement for School of Keio (Japan), 2. University of Keio OLED Displays in Power-constrained Conditions (Japan), 3. Panasonic Corporation (Japan)) *Hsuan-Chi Huang1, Pei-Li Sun1 (1. National Taiwan 4:05 PM - 4:25 PM University of Science and Technology (Taiwan)) [VHF2-4] The Evaluation for Visibility of a Back Image 2:05 PM - 2:25 PM on a Transparent Display [VHF1-3] Estimation of Equivalent Conditions for *Naruki Yamada1, Yoshinori Iguchi1, Yukihiro Tao1 Display Sparkle Measurement (1. -

Flexible Quantum Dot Light-Emitting Diodes for Next-Generation Displays
www.nature.com/npjflexelectron REVIEW ARTICLE OPEN Flexible quantum dot light-emitting diodes for next-generation displays Moon Kee Choi1,2, Jiwoong Yang1,2, Taeghwan Hyeon1,2 and Dae-Hyeong Kim1,2 In the future electronics, all device components will be connected wirelessly to displays that serve as information input and/or output ports. There is a growing demand of flexible and wearable displays, therefore, for information input/output of the next- generation consumer electronics. Among many kinds of light-emitting devices for these next-generation displays, quantum dot light-emitting diodes (QLEDs) exhibit unique advantages, such as wide color gamut, high color purity, high brightness with low turn-on voltage, and ultrathin form factor. Here, we review the recent progress on flexible QLEDs for the next-generation displays. First, the recent technological advances in device structure engineering, quantum-dot synthesis, and high-resolution full-color patterning are summarized. Then, the various device applications based on cutting-edge quantum dot technologies are described, including flexible white QLEDs, wearable QLEDs, and flexible transparent QLEDs. Finally, we showcase the integration of flexible QLEDs with wearable sensors, micro-controllers, and wireless communication units for the next-generation wearable electronics. npj Flexible Electronics (2018) 2:10 ; doi:10.1038/s41528-018-0023-3 INTRODUCTION Bendable displays can be utilized as foldable tablets whose screen Flexible displays have received significant attention owing to their sizes are tunable (Fig. 1e). Moreover, transparent flexible displays potential applications to mobile and wearable electronics1,2 such can be used for smart windows or digital signage, which can as smartphones, automotive displays, and wearable smart devices. -

Quantum Dot Physics: a Guide to Understanding QD Displays
Public Information Display Quantum Dot Physics: A Guide to Understanding QD Displays Abstract This whitepaper aims to establish the foundation for a thorough understanding of the science behind the quantum dot (QD) technology and its popular and promising application in quantum dot displays. Equipped with this knowledge, you will be able to confidently follow the technology evolution as the industry is making new breakthroughs and is further improving upon QD utilization in displays. As nanotechnology has already become a vital foundation of the high-end displays, we expand upon the topic of quantum dots to examine the key properties of the QD semiconductor particles and fundamental principles of their operation. Quantum dots fundamentals What are quantum dots? Quantum dots (QDs) are tiny semiconductor particles 2-10 nm (nanometers, 10^-9) in diameter. Because of their small size, these particles have unique optical and electrical properties. For example, when exposed to light, quantum dot crystals emit light of particular frequencies. The size and shape of quantum dots can be precisely controlled by adjusting reaction time and conditions, thus making this nanotechnology scalable and useful for display applications. How do quantum dots work? Let's dig deeper into quantum physics (do not be intimidated though) to explore why quantum dots (QDs) are able to emit light and why the wavelength of the light (which determines color) they produce is contingent on the particle size. The process of light emission in QDs is called photoluminescence (abbreviated as PL), as it occurs because of the excitation by photons. Under the influence of light, photons get excited and “jump” up to a higher energy band. -
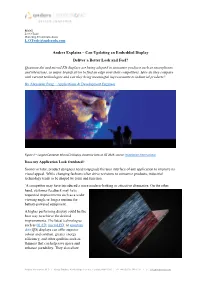
Anders Explains – Can Updating an Embedded Display Deliver a Better
BLOG Lee O’Toole Marketing & Communications [email protected] Anders Explains – Can Updating an Embedded Display Deliver a Better Look and Feel? Quantum dot and microLED displays are being adopted in consumer products such as smartphones and televisions, as major brands strive to find an edge over their competitors. How do they compare with current technologies and can they bring meaningful improvements to industrial products? By Alexander Pang – Applications & Development Engineer Figure 1 – Largest European MicroLED Display shown by Sony at ISE 2019, source: Installation International Does my Application Look Outdated? Sooner or later, product designers need to upgrade the user interface of any application to improve its visual appeal. While changing fashions often drive revisions to consumer products, industrial technology tends to be shaped by form and function. `A competitor may have introduced a more modern-looking or attractive alternative. On the other hand, customer feedback may have requested improvements such as a wider viewing angle or longer runtime for battery-powered equipment. A higher performing display could be the best way to achieve the desired improvements. The latest technologies such as OLED, microLED, or quantum dot (QD) displays can offer superior colour and contrast, greater energy efficiency, and other qualities such as thinness that can help save space and enhance portability. They also allow Anders Electronics PLC I Kings Studios, 43-45 Kings Terrace, London, NW1 0JR I +44 (0)207 388 7171 I : [email protected] novel capabilities such as rollable or foldable displays. What are the Best Display Technologies for Industrial Applications? Right now, the proven TFT-LCD is the colour-display technology chosen for most industrial applications. -
2017 IMID.Hwp
CONTENTS Welcome Message ····································································· 4 Program Overview - Tutorials ················································································· 6 - Workshops ············································································ 6 - Keynote Addresses ································································ 7 - Industrial Forum ···································································· 8 - Young Leaders Conference ·················································· 9 - YLC Awards ··········································································· 9 - Social Events ·········································································· 9 - IMID 2017 Awards ······························································ 10 IMID 2017 Awarded Papers ····················································· 11 Useful Information - Venue ·················································································· 12 - Registration ········································································· 12 - Internet ················································································ 13 - Cloak Room & Lost and Found ·········································· 13 - Tax ························································································ 14 - Tipping ················································································ 14 - Electricity (220V) ·································································