DOCSLIB.ORG

Controlling Portfolio Skewness and Kurtosis Without Directly Optimizing Third and Fourth Moments

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Controlling Portfolio Skewness and Kurtosis Without Directly Optimizing Third and Fourth Moments Economics Letters 122 (2014) 154–158 Contents lists available at ScienceDirect Economics Letters journal homepage: www.elsevier.com/locate/ecolet Controlling portfolio skewness and kurtosis without directly optimizing third and fourth moments Woo Chang Kim a,∗, Frank J. Fabozzi b, Patrick Cheridito c, Charles Fox d a Department of Industrial and Systems Engineering, Korea Advanced Institute of Science and Technology (KAIST), 91 Daehak-ro, Yuseong-gu, Daejeon 305-701, Republic of Korea b EDHEC Business School, 393, Promenade des Anglais BP3116, 06202 Nice Cedex 3, Nice, France c Department of Operations Research and Financial Engineering, Princeton University, Sherrerd Hall, Princeton University, Princeton, NJ 08542, USA d Pimco, 840 Newport Circle Dr. Newport Beach, CA 92660, USA h i g h l i g h t s • We propose a new mean–variance approach that can control higher moments. • Our model does not directly impose higher moment terms in the formulation. • Our model employs robust formulation with a specific choice of uncertainty set. • We provide analytical proofs showing our model can control higher moments. • We present empirical results supporting the validity of our model. article info a b s t r a c t Article history: In spite of their importance, third or higher moments of portfolio returns are often neglected in portfo- Received 23 August 2013 lio construction problems due to the computational difficulties associated with them. In this paper, we Received in revised form propose a new robust mean–variance approach that can control portfolio skewness and kurtosis without 19 November 2013 imposing higher moment terms. The key idea is that, if the uncertainty sets are properly constructed, ro- Accepted 20 November 2013 bust portfolios based on the worst-case approach within the mean–variance setting favor skewness and Available online 1 December 2013 penalize kurtosis. ' 2013 Elsevier B.V. All rights reserved. JEL classification: G11 C61 C63 C65 Keywords: Portfolio selection Robust portfolio Higher moments Mean–variance framework 1. Introduction skewed, it is more likely to have an extreme left-tail event than one in the right-tail. Thus the typical investor prefers more posi- The traditional Markowitz model takes the expectation and tively skewed return distributions. For instance, a more positively variance of a portfolio return as the performance and risk measures skewed portfolio has better Sortino ratio (Sortino and van der and determines the optimal portfolio by solving a quadratic pro- Meer, 1991) and lower semi-deviation. Similarly, a portfolio with gram. From the practitioner's perspective, the skewness and kur- smaller kurtosis tends to have less extreme events, thus is pre- tosis are also important. When the portfolio return is negatively ferred by most investors. Obviously, as the traditional mean–variance approach exclu- sively deals with the first two moments, a revised approach is re- ∗ quired to incorporate and control the third and fourth moments Corresponding author. Tel.: +82 42 350 3129. when constructing a portfolio. The most straightforward approach E-mail addresses: [email protected], [email protected] (W.C. Kim), [email protected] (F.J. Fabozzi), [email protected] (P. Cheridito), would be to introduce new terms for the portfolio skewness and [email protected] (C. Fox). kurtosis in the objective function. To see this, let us first consider 0165-1765/$ – see front matter ' 2013 Elsevier B.V. All rights reserved. http://dx.doi.org/10.1016/j.econlet.2013.11.024 W.C. Kim et al. / Economics Letters 122 (2014) 154–158 155 2 2 3 the traditional mean–variance formulation as follows. In addition, let µ D EXi;j; σ D E Xi;j − µ ; µ3 D E Xi;j − µ 4 0 0 D − D max µ w − βw Σw (1) and µ4 E Xi;j µ . Also, for i 1;:::; I, we define w2C VD O 0 − 0 O D N − 2 fi.w/ µiw βw Σiw Xi βSi ; where C is a convex subset of the hyperplane fw 2 nj P w D R i i 0 0 O g 2 n 2 n×n f .w/ VD min µO w − βw Σw D min fi.w/: 1 ; µ R ; Σ R are the expected return and covariance ma- O i .µ,O Σ/2U O trix, respectively, and β > 0 is the parameter to reflect investor's .µ,O Σ/ risk aversion. We first give a limit result for f .w/ when J ! 1. 0 i Then, given a coskewness matrix M3 D ET.r−Er/.r−Er/ ⊗.r− 0 n×n2 n 2 Er/ U 2 R for the random return vector r 2 R and Kronecker Theorem 2.1. For every w C, one has ⊗ 0 product , the third central moment of portfolio return w r is p d 2 2 4 2 0 0 3 0 J [fi.w/ − Efi.w/] −! N.0; σ − β σ − 2βµ3 C β µ4/ S .w; M3/ VD E w r − Ew r D w M3 .w ⊗ w/. Similarly, for a 0 0 for J ! 1: cokurtosis matrix M4 D E .r − Er/.r − Er/ ⊗ .r − Er/ ⊗ .r− 0 n×n3 0 Er/ 2 R , its fourth central moment is K .w; M4/ VD E w r− Proof. Consider 0 4 0 Ew r D w M4 .w ⊗ w ⊗ w/. p J [fi.w/ − Efi.w/] Consequently, the mean–variance formulation could be modi- ! fied by adding third and fourth central moments and solving the p N β X N 2 p 2 D J Xi − Xi;j − Xi − J µ − βσ optimization problem J − 1 j 0 0 max µ w − βw Σw C γ S .w; M3/ − δK .w; M4/ " ( )# w2C p N β X N 2 2 D J Xi − Xi;j − µ − Xi − µ C S J i for parameters β; γ ; δ ≥ 0: (2) j − p − 2 While problem (2) is intuitive, there are two critical issues. First, J µ βσ the third central moment term S .w; M3/ is a cubic function, thus it p N β X 2 N 2 D J Xi − Xi;j − µ − 2J Xi − µ makes problem (2) non-convex, which causes a significant increase J j in computational cost. Second, as the coskewness matrix M3 is 3-dimensional, the number of parameters is of the order of n3, C N − 2 C 2 − p − 2 which makes it practically impossible to obtain reliable estimators. J Xi µ Si J µ βσ The same issues apply to the kurtosis term, only with more diffi- " culties. The main objective of this study is to develop an approach p 1 X β X 2 D J Xi;j − Xi;j − µ that can control higher moments of portfolio returns within the J J j j mean–variance framework without directly imposing third and # fourth moment terms in the formulation. N 2 β 2 p 2 C β Xi − µ − S − J µ − βσ J i 2. Models and theories " # p 1 X 2 2 n D J fXi;j − β.Xi;j − µ) g − (µ − βσ / Let r 2 R be the random vector representing returns of n risky J assets. We assume it has finite moments up to order four. Also, let j n | {z } ri;j 2 R for i D 1;:::; I, and j D 1;:::; J be independent and .a/ identically distributed (i.i.d.) samples of r. Let µO D 1 P r and i J j i;j p N 2 β 2 0 C Jβ.Xi − µ) − p S : ΣO D 1 P r − O r − O be the sample mean and sample J i i J−1 j i;j µi i;j µi | {z } covariance matrix for the i-th sample set, respectively. We also de- .b/ | {z } .c/ O O D O O fine a joint uncertainty set of µ, Σ ; U µ,O ΣO µ1; Σ1 ;:::; h n oi . / 1 P 2 2 Since E Xi;j − β Xi;j − µ D µ − βσ , by the Cen- O O O O J j µi; Σi ;:::; µI ; ΣI Now, let us consider the robust version h −!d − − 2 of problem (1). tral Limit Theorem (CLT), .a/ N 0; Var Xi;j β Xi;j µ . N − −!P O 0 − 0 O Next, Since Xi µ 0 by the Weak Law of Large Numbers, and max min µ w βw Σw: (3) p d d w2C µ,O ΣO 2U N − −! 2 −! . / .µ,O ΣO / J Xi µ N 0; σ by CLT, by Slutsky's Theorem, .b/ 0. P P Finally, since p1 ! 0 and S2 −! σ 2;.c/ −! 0. Thus, again by For a feasible portfolio w of problem (3), let J i Slutsky's Theorem, 0 Xi;j D w ri;j; p d h 2 J [fi.w/ − fi.w/] −! N 0; ar Xi;j − β Xi;j − µ : J J E V N 1 X 0 1 X Xi D w ri;j D Xi;j; h 2i h 2i J J − D − D − jD1 jD1 Since Cov Xi;j; Xi;j µ µ3 and Var Xi;j µ µ4 4 J ! σ , 2 1 0 X 0 D − O − O h 2i Si w ri;j µi ri;j µi w J − 1 Var Xi;j − β Xi;j − µ jD1 h 2i 2 h 2i J D Var Xi;j − 2β Cov Xi;j; Xi;j − µ C β Var Xi;j − µ 1 X N 2 D Xi;j − Xi : J − 1 D 2 − C 2 − 2 4 jD1 σ 2βµ3 β µ4 β σ : 156 W.C.
Load more

Recommended publications
  • Use of Proc Iml to Calculate L-Moments for the Univariate Distributional Shape Parameters Skewness and Kurtosis
    Statistics 573 USE OF PROC IML TO CALCULATE L-MOMENTS FOR THE UNIVARIATE DISTRIBUTIONAL SHAPE PARAMETERS SKEWNESS AND KURTOSIS Michael A. Walega Berlex Laboratories, Wayne, New Jersey Introduction Exploratory data analysis statistics, such as those Gaussian. Bickel (1988) and Van Oer Laan and generated by the sp,ge procedure PROC Verdooren (1987) discuss the concept of robustness UNIVARIATE (1990), are useful tools to characterize and how it pertains to the assumption of normality. the underlying distribution of data prior to more rigorous statistical analyses. Assessment of the As discussed by Glass et al. (1972), incorrect distributional shape of data is usually accomplished conclusions may be reached when the normality by careful examination of the values of the third and assumption is not valid, especially when one-tail tests fourth central moments, skewness and kurtosis. are employed or the sample size or significance level However, when the sample size is small or the are very small. Hopkins and Weeks (1990) also underlying distribution is non-normal, the information discuss the effects of highly non-normal data on obtained from the sample skewness and kurtosis can hypothesis testing of variances. Thus, it is apparent be misleading. that examination of the skewness (departure from symmetry) and kurtosis (deviation from a normal One alternative to the central moment shape statistics curve) is an important component of exploratory data is the use of linear combinations of order statistics (L­ analyses. moments) to examine the distributional shape characteristics of data. L-moments have several Various methods to estimate skewness and kurtosis theoretical advantages over the central moment have been proposed (MacGillivray and Salanela, shape statistics: Characterization of a wider range of 1988).
    [Show full text]
  • A Skew Extension of the T-Distribution, with Applications
    J. R. Statist. Soc. B (2003) 65, Part 1, pp. 159–174 A skew extension of the t-distribution, with applications M. C. Jones The Open University, Milton Keynes, UK and M. J. Faddy University of Birmingham, UK [Received March 2000. Final revision July 2002] Summary. A tractable skew t-distribution on the real line is proposed.This includes as a special case the symmetric t-distribution, and otherwise provides skew extensions thereof.The distribu- tion is potentially useful both for modelling data and in robustness studies. Properties of the new distribution are presented. Likelihood inference for the parameters of this skew t-distribution is developed. Application is made to two data modelling examples. Keywords: Beta distribution; Likelihood inference; Robustness; Skewness; Student’s t-distribution 1. Introduction Student’s t-distribution occurs frequently in statistics. Its usual derivation and use is as the sam- pling distribution of certain test statistics under normality, but increasingly the t-distribution is being used in both frequentist and Bayesian statistics as a heavy-tailed alternative to the nor- mal distribution when robustness to possible outliers is a concern. See Lange et al. (1989) and Gelman et al. (1995) and references therein. It will often be useful to consider a further alternative to the normal or t-distribution which is both heavy tailed and skew. To this end, we propose a family of distributions which includes the symmetric t-distributions as special cases, and also includes extensions of the t-distribution, still taking values on the whole real line, with non-zero skewness. Let a>0 and b>0be parameters.
    [Show full text]
  • 1. How Different Is the T Distribution from the Normal?
    Statistics 101–106 Lecture 7 (20 October 98) c David Pollard Page 1 Read M&M §7.1 and §7.2, ignoring starred parts. Reread M&M §3.2. The eects of estimated variances on normal approximations. t-distributions. Comparison of two means: pooling of estimates of variances, or paired observations. In Lecture 6, when discussing comparison of two Binomial proportions, I was content to estimate unknown variances when calculating statistics that were to be treated as approximately normally distributed. You might have worried about the effect of variability of the estimate. W. S. Gosset (“Student”) considered a similar problem in a very famous 1908 paper, where the role of Student’s t-distribution was first recognized. Gosset discovered that the effect of estimated variances could be described exactly in a simplified problem where n independent observations X1,...,Xn are taken from (, ) = ( + ...+ )/ a normal√ distribution, N . The sample mean, X X1 Xn n has a N(, / n) distribution. The random variable X Z = √ / n 2 2 Phas a standard normal distribution. If we estimate by the sample variance, s = ( )2/( ) i Xi X n 1 , then the resulting statistic, X T = √ s/ n no longer has a normal distribution. It has a t-distribution on n 1 degrees of freedom. Remark. I have written T , instead of the t used by M&M page 505. I find it causes confusion that t refers to both the name of the statistic and the name of its distribution. As you will soon see, the estimation of the variance has the effect of spreading out the distribution a little beyond what it would be if were used.
    [Show full text]
  • Information-Theoretic Approaches to Portfolio Selection
    Information-theoretic approaches to portfolio selection Nathan LASSANCE Doctoral Thesis 2 | 2020 Université catholique de Louvain LOUVAIN INSTITUTE OF DATA ANALYSIS AND MODELING IN ECONOMICS AND STATISTICS (LIDAM) Universite´ catholique de Louvain Louvain School of Management LIDAM & Louvain Finance Doctoral Thesis Information-theoretic approaches to portfolio selection Nathan Lassance Thesis submitted in partial fulfillment of the requirements for the degree of Docteur en sciences ´economiques et de gestion Dissertation committee: Prof. Fr´ed´ericVrins (UCLouvain, BE), Advisor Prof. Kris Boudt (Ghent University, BE) Prof. Victor DeMiguel (London Business School, UK) Prof. Guofu Zhou (Washington University, USA) Prof. Marco Saerens (UCLouvain, BE), President Academic year 2019-2020 \Find a job you enjoy doing, and you will never have to work a day in your life." Mark Twain Contents Abstract vii Acknowledgments ix Research accomplishments xii List of Figures xii List of Tables xv List of Notation xvii Introduction1 1 Research background7 1.1 Mean-variance approaches..........................7 1.1.1 Definitions...............................8 1.1.2 Estimation risk............................ 10 1.1.3 Robust mean-variance portfolios................... 13 1.2 Higher-moment approaches.......................... 19 1.2.1 Efficient portfolios.......................... 21 1.2.2 Downside-risk criteria......................... 23 1.2.3 Indirect approaches.......................... 25 1.3 Risk-parity approaches............................ 25 1.3.1 Asset-risk parity........................... 26 1.3.2 Factor-risk parity........................... 28 1.3.3 Criticisms............................... 29 1.4 Information-theoretic approaches...................... 30 1.5 Thesis contributions............................. 32 2 Minimum R´enyi entropy portfolios 35 2.1 Introduction.................................. 35 2.2 The notion of entropy............................ 36 2.2.1 Shannon entropy........................... 37 2.2.2 R´enyi entropy............................
    [Show full text]
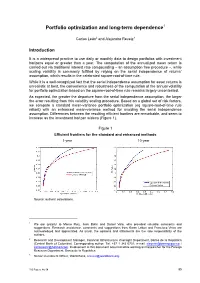
  • Portfolio Optimization and Long-Term Dependence1
    Portfolio optimization and long-term dependence1 Carlos León2 and Alejandro Reveiz3 Introduction It is a widespread practice to use daily or monthly data to design portfolios with investment horizons equal or greater than a year. The computation of the annualized mean return is carried out via traditional interest rate compounding – an assumption free procedure –, while scaling volatility is commonly fulfilled by relying on the serial independence of returns’ assumption, which results in the celebrated square-root-of-time rule. While it is a well-recognized fact that the serial independence assumption for asset returns is unrealistic at best, the convenience and robustness of the computation of the annual volatility for portfolio optimization based on the square-root-of-time rule remains largely uncontested. As expected, the greater the departure from the serial independence assumption, the larger the error resulting from this volatility scaling procedure. Based on a global set of risk factors, we compare a standard mean-variance portfolio optimization (eg square-root-of-time rule reliant) with an enhanced mean-variance method for avoiding the serial independence assumption. Differences between the resulting efficient frontiers are remarkable, and seem to increase as the investment horizon widens (Figure 1). Figure 1 Efficient frontiers for the standard and enhanced methods 1-year 10-year Source: authors’ calculations. 1 We are grateful to Marco Ruíz, Jack Bohn and Daniel Vela, who provided valuable comments and suggestions. Research assistance, comments and suggestions from Karen Leiton and Francisco Vivas are acknowledged and appreciated. As usual, the opinions and statements are the sole responsibility of the authors.
    [Show full text]
  • On the Meaning and Use of Kurtosis
    Psychological Methods Copyright 1997 by the American Psychological Association, Inc. 1997, Vol. 2, No. 3,292-307 1082-989X/97/$3.00 On the Meaning and Use of Kurtosis Lawrence T. DeCarlo Fordham University For symmetric unimodal distributions, positive kurtosis indicates heavy tails and peakedness relative to the normal distribution, whereas negative kurtosis indicates light tails and flatness. Many textbooks, however, describe or illustrate kurtosis incompletely or incorrectly. In this article, kurtosis is illustrated with well-known distributions, and aspects of its interpretation and misinterpretation are discussed. The role of kurtosis in testing univariate and multivariate normality; as a measure of departures from normality; in issues of robustness, outliers, and bimodality; in generalized tests and estimators, as well as limitations of and alternatives to the kurtosis measure [32, are discussed. It is typically noted in introductory statistics standard deviation. The normal distribution has a kur- courses that distributions can be characterized in tosis of 3, and 132 - 3 is often used so that the refer- terms of central tendency, variability, and shape. With ence normal distribution has a kurtosis of zero (132 - respect to shape, virtually every textbook defines and 3 is sometimes denoted as Y2)- A sample counterpart illustrates skewness. On the other hand, another as- to 132 can be obtained by replacing the population pect of shape, which is kurtosis, is either not discussed moments with the sample moments, which gives or, worse yet, is often described or illustrated incor- rectly. Kurtosis is also frequently not reported in re- ~(X i -- S)4/n search articles, in spite of the fact that virtually every b2 (•(X i - ~')2/n)2' statistical package provides a measure of kurtosis.
    [Show full text]
  • A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess
    S S symmetry Article A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess Guillermo Martínez-Flórez 1, Víctor Leiva 2,* , Emilio Gómez-Déniz 3 and Carolina Marchant 4 1 Departamento de Matemáticas y Estadística, Facultad de Ciencias Básicas, Universidad de Córdoba, Montería 14014, Colombia; [email protected] 2 Escuela de Ingeniería Industrial, Pontificia Universidad Católica de Valparaíso, 2362807 Valparaíso, Chile 3 Facultad de Economía, Empresa y Turismo, Universidad de Las Palmas de Gran Canaria and TIDES Institute, 35001 Canarias, Spain; [email protected] 4 Facultad de Ciencias Básicas, Universidad Católica del Maule, 3466706 Talca, Chile; [email protected] * Correspondence: [email protected] or [email protected] Received: 30 June 2020; Accepted: 19 August 2020; Published: 1 September 2020 Abstract: In this paper, we consider skew-normal distributions for constructing new a distribution which allows us to model proportions and rates with zero/one inflation as an alternative to the inflated beta distributions. The new distribution is a mixture between a Bernoulli distribution for explaining the zero/one excess and a censored skew-normal distribution for the continuous variable. The maximum likelihood method is used for parameter estimation. Observed and expected Fisher information matrices are derived to conduct likelihood-based inference in this new type skew-normal distribution. Given the flexibility of the new distributions, we are able to show, in real data scenarios, the good performance of our proposal. Keywords: beta distribution; centered skew-normal distribution; maximum-likelihood methods; Monte Carlo simulations; proportions; R software; rates; zero/one inflated data 1.
    [Show full text]
  • Volatility Modeling Using the Student's T Distribution
    Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Economics Aris Spanos, Chair Richard Ashley Raman Kumar Anya McGuirk Dennis Yang August 29, 2003 Blacksburg, Virginia Keywords: Student’s t Distribution, Multivariate GARCH, VAR, Exchange Rates Copyright 2003, Maria S. Heracleous Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous (ABSTRACT) Over the last twenty years or so the Dynamic Volatility literature has produced a wealth of uni- variateandmultivariateGARCHtypemodels.Whiletheunivariatemodelshavebeenrelatively successful in empirical studies, they suffer from a number of weaknesses, such as unverifiable param- eter restrictions, existence of moment conditions and the retention of Normality. These problems are naturally more acute in the multivariate GARCH type models, which in addition have the problem of overparameterization. This dissertation uses the Student’s t distribution and follows the Probabilistic Reduction (PR) methodology to modify and extend the univariate and multivariate volatility models viewed as alternative to the GARCH models. Its most important advantage is that it gives rise to internally consistent statistical models that do not require ad hoc parameter restrictions unlike the GARCH formulations. Chapters 1 and 2 provide an overview of my dissertation and recent developments in the volatil- ity literature. In Chapter 3 we provide an empirical illustration of the PR approach for modeling univariate volatility. Estimation results suggest that the Student’s t AR model is a parsimonious and statistically adequate representation of exchange rate returns and Dow Jones returns data.
    [Show full text]
  • Approximating the Distribution of the Product of Two Normally Distributed Random Variables
    S S symmetry Article Approximating the Distribution of the Product of Two Normally Distributed Random Variables Antonio Seijas-Macías 1,2 , Amílcar Oliveira 2,3 , Teresa A. Oliveira 2,3 and Víctor Leiva 4,* 1 Departamento de Economía, Universidade da Coruña, 15071 A Coruña, Spain; [email protected] 2 CEAUL, Faculdade de Ciências, Universidade de Lisboa, 1649-014 Lisboa, Portugal; [email protected] (A.O.); [email protected] (T.A.O.) 3 Departamento de Ciências e Tecnologia, Universidade Aberta, 1269-001 Lisboa, Portugal 4 Escuela de Ingeniería Industrial, Pontificia Universidad Católica de Valparaíso, Valparaíso 2362807, Chile * Correspondence: [email protected] or [email protected] Received: 21 June 2020; Accepted: 18 July 2020; Published: 22 July 2020 Abstract: The distribution of the product of two normally distributed random variables has been an open problem from the early years in the XXth century. First approaches tried to determinate the mathematical and statistical properties of the distribution of such a product using different types of functions. Recently, an improvement in computational techniques has performed new approaches for calculating related integrals by using numerical integration. Another approach is to adopt any other distribution to approximate the probability density function of this product. The skew-normal distribution is a generalization of the normal distribution which considers skewness making it flexible. In this work, we approximate the distribution of the product of two normally distributed random variables using a type of skew-normal distribution. The influence of the parameters of the two normal distributions on the approximation is explored. When one of the normally distributed variables has an inverse coefficient of variation greater than one, our approximation performs better than when both normally distributed variables have inverse coefficients of variation less than one.
    [Show full text]
  • Calculating Variance and Standard Deviation
    VARIANCE AND STANDARD DEVIATION Recall that the range is the difference between the upper and lower limits of the data. While this is important, it does have one major disadvantage. It does not describe the variation among the variables. For instance, both of these sets of data have the same range, yet their values are definitely different. 90, 90, 90, 98, 90 Range = 8 1, 6, 8, 1, 9, 5 Range = 8 To better describe the variation, we will introduce two other measures of variation—variance and standard deviation (the variance is the square of the standard deviation). These measures tell us how much the actual values differ from the mean. The larger the standard deviation, the more spread out the values. The smaller the standard deviation, the less spread out the values. This measure is particularly helpful to teachers as they try to find whether their students’ scores on a certain test are closely related to the class average. To find the standard deviation of a set of values: a. Find the mean of the data b. Find the difference (deviation) between each of the scores and the mean c. Square each deviation d. Sum the squares e. Dividing by one less than the number of values, find the “mean” of this sum (the variance*) f. Find the square root of the variance (the standard deviation) *Note: In some books, the variance is found by dividing by n. In statistics it is more useful to divide by n -1. EXAMPLE Find the variance and standard deviation of the following scores on an exam: 92, 95, 85, 80, 75, 50 SOLUTION First we find the mean of the data: 92+95+85+80+75+50 477 Mean = = = 79.5 6 6 Then we find the difference between each score and the mean (deviation).
    [Show full text]
  • Margrabe Formulas for a Simple Bivariate Exponential Variance-Gamma Price Process (II) Statistical Estimation and Application
    International Journal of Scientific and Innovative Mathematical Research (IJSIMR) Volume I, Issue I, August- 2013, PP 33-44 www.arcjournals.org Margrabe Formulas for a Simple Bivariate Exponential Variance-Gamma Price Process (II) Statistical Estimation and Application Werner Hürlimann Wolters Kluwer Financial Services, Seefeldstrasse 69, CH-8008 Zürich, Switzerland. [email protected] Received: 20-06-2013 Revised: 21-07-2013 Accepted: 24-07-2013 Abstract: A multivariate moment method for the simple multivariate variance-gamma distribution is considered. It takes into account the star products of both the coskewness and cokurtosis tensors. The model parameters depend upon the solution of a sextic equation, and the covariance matrix is functionally dependent upon coskweness and cokurtosis. The method enables simultaneous estimation of the parameters given sample estimates of the mean vector, coskewness vector and cokurtosis matrix. Application to the estimation of the bivariate variance-gamma model for the Standard & Poors 500 and NASDAQ 100 stock market indices is undertaken. The statistical fitting results are used to compare the original Margrabe formula with a variance-gamma exchange option pricing formula derived through application of the state- price deflator approach. Keywords: multivariate variance-gamma, coskewness, cokurtosis, exchange option, stock market. 1. INTRODUCTION In the first part of the present study, a simple multivariate exponential variance-gamma price process has been considered as alternative to the usual multivariate exponential Gaussian process. Based on it a state-price deflator has been constructed and applied to derive pricing formulas for the exchange option with a bivariate exponential variance-gamma deflated price process. It has been observed that the simple model is easy to work with but has some serious drawbacks.
    [Show full text]
  • Phd Dissertation
    ©Copyright 2010 Minfeng Zhu Portfolio Optimization with Tail Risk Measures and Non-Normal Returns Minfeng Zhu A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Washington 2010 Program Authorized to Offer Degree: Department of Statistics University of Washington Graduate School This is to certify that I have examined this copy of a doctoral dissertation by Minfeng Zhu and have found that it is complete and satisfactory in all respects, and that any and all revisions required by the final examining committee have been made. Chair of the Supervisory Committee: R. Douglas Martin Reading Committee: R. Douglas Martin Andrew Clark Eric W Zivot Date: In presenting this dissertation in partial fulfillment of the requirements for the doctoral degree at the University of Washington, I agree that the Library shall make its copies freely available for inspection. I further agree that extensive copying of the dissertation is allowable only for scholarly purposes, consistent with “fair use” as prescribed in the U.S. Copyright Law. Requests for copying or reproduction of this dissertation may be referred to ProQuest Information and Learning, 300 North Zeeb Road, Ann Arbor, MI 48106- 1346, 1-800-521-0600, to whom the author has granted “the right to reproduce and sell (a) copies of the manuscript in microform and/or (b) printed copies of the manuscript made from microform.” Signature ________________________ Date ____________________________ University of Washington Abstract Portfolio Optimization with Tail Risk Measures and Non-Normal Returns Minfeng Zhu Chair of the Supervisory Committee: Professor R. Douglas Martin Department of Statistics The traditional Markowitz mean-variance portfolio optimization theory uses volatility as the sole measure of risk.
    [Show full text]