DOCSLIB.ORG

Development of Agents for Creating Melodies and Investigation of Interaction Between the Agents

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Development of Agents for Creating Melodies and Investigation of Interaction Between the Agents Development of Agents for Creating Melodies and Investigation of Interaction between the Agents Hidefumi Ohmura1, Takuro Shibayama2, Keiji Hirata3 and Satoshi Tojo4 1Department of Information Sciences, Tokyo University of Science, 2641 Yamazaki, Noda-shi, Chiba, Japan 2Department of Information Systems and Design, Tokyo Denki University, Ishizaka, Hatoyama-cho, Hikigun, Saitama, Japan 3Department of Complex and Intelligent Systems, Future University Hakodate, 116-2, Kamedanakano-cho, Hakodate-shi, Hokkaido, Japan 4Graduate School of Information Science, Japan Advanced Institute of Science and Technology, 1-1 Asahidai, Nomi-shi, Ishikawa, Japan Keywords: Music, Melody, Lattice Space. Abstract: In this study, we attempted to construct computational musical theory by creating musical structure using physical features of sound without relying on the existing musical theory. Subsequently, we developed an agent system to create melodies. The agents can select the next note (a sound timing and a pitch) depending on the lattice spaces consisting of physical relationships (ratios) and probabilities. Further, we improve the agents which are interacting with each other in the system, and the system outputs various sounds such as music. We confirmed that the system could create structures of musical theory, such as mode, scale, and rhythm. The advantages and disadvantages of the lattice spaces are discovered. 1 INTRODUCTION ing the hypothesis. Next, we show the agent system creating melodies, and how agents interact with each Most human beings can hum and whistle melodies in other. Subsequently, we describe the system with an improvisational way in their daily lives. This gen- agents and the operation of the system. Finally, we eration of melodies is considered a beneficial human discuss music as the output of the system. quality for surviving in society (Jordania, 2010). In- terestingly, children can also hum melodies without music education. 2 MUSICAL FEATURES We considered how they create melodies and de- veloped an agent system creating melodies (Ohmura 2.1 Hypothesis of Creating Melodies et al., 2018). The system can provide computational musical structures such as musical scale and mode in It is typical for a musically educated person to eas- music theory because we adopted lattice spaces de- ily select the next pitch and next sound timing of ap- pending on the physical relationships of sounds to the propriateness of a present note. However, the ques- system. tion arises as to why both adults and children with- In this study, we aim to improve the agent sys- out musical education can hum or whistle melodies. tem including the three agents that interact with each We generate the following hypothesis regarding the other. We herein detail the basic elements of the pre- selection of the next note except in the case of recol- vious system in creating melodies, and demonstrate lecting a melody. “They select purely a note of physi- the improved features. Subsequently, we discuss the cal proximity to the present note.” Physical proximity outputs from the system as the music is created by the includes two elements. The first element is the rela- interactions between agents. tionship between the sound timings of notes. The sec- First, we propose a hypothesis on how humans ond element is the relationship between the pitches of create melodies such as humming and whistling, and notes. We considered how they create the melodies demonstrate the physical features of sounds underly- and developed an agent system creating melodies 307 Ohmura, H., Shibayama, T., Hirata, K. and Tojo, S. Development of Agents for Creating Melodies and Investigation of Interaction between the Agents. DOI: 10.5220/0007702303070314 In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 307-314 ISBN: 978-989-758-350-6 Copyright c 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved HAMT 2019 - Special Session on Human-centric Applications of Multi-agent Technologies based on the hypothesis(Ohmura et al., 2018). In this and are defined by the relationship between the fre- section, we explain their relationships and detail the quencies. theories of musical expectation to demonstrate how A relationship of 1:2 creates an interval of a per- an agent selects a note. fect octave, and a relationship of 1:3 creates an inter- val of a perfect fifteenth, which is two octaves. The 2.2 Relationships between Pulses (Note relationship of 2:3 and 3:2 are combined duple and Values) triple frequencies (see Figure 2). This pattern is called a perfect fifth. The relationships of 3:4 and 4:3 are combined triple and quadruple (see Figure 2). This In music, an iteration is an important primitive pat- pattern is called a perfect fourth, which is a consonant tern, and a pulse is the most primitive element in a interval following a perfect fifth. rhythm. For example, when a listener hears two pulses (whose relationship is 1:2), he/she may feel a duple 880Hz 990Hz meter (see Figure 1). When a relationship is 1:3, a (A5) ! 4/3 ! 3/2 (B5) listener may perceive a triple meter. ! 3/4 ! 2/3 Next, we consider 2:3 and 3:2 ratios combining 660Hz duple and triple meters. These relationships provide ! 1/2 ! 2 ! 1/2 ! 2 (E5) the listener with a polyrhythm. A listener perceives ! 3/2 ! 4/3 one basic pulse as an upbeat, and another as a down- ! 2/3 ! 3/4 beat. In the cases of 3:4 and 4:3, a listener perceives a polyrhythm consisting of triple and quadruple meters. 440Hz 495Hz (A4) (B4) Figure 2: Relationships between pitch (intervals). The Pythagorean scale (and principle of the Sanfen × 2 × 1/2 Sunyi) involve only the relationships of duples and × 3 × 3 triples. However, depending on temperament, some intervals are imprecise. × 1/3 × 1/3 In the case of intervals, a quintuple is important. × 1/2 × 2 In particular, in a relationship between three pitches, a 3:4:5 creates a consonance code, called a major triad. A relationship consisting of a double, triple, and quin- tuple creates intonation. In this study, however, we Figure 1: Relationships between pulses (note values). employ only the double and triple for a simple and Actual music consists of many pulses. A listener per- easy operation. ceives the strongest or most-frequent pulse as the me- ter of the music, and less-frequent pulses as weak 2.4 Theories of Musical Expectation beats and up beats. Monophony, however, lacks beats, such that a listener at times may not perceive any me- We attempted to control the musical expectations ter. This is true in the melodies of humming. based on the theories of musical expectations (Ohmura et al., 2016). Here, we introduce these theo- ries that provide how an agent selects the next note. 2.3 Relationships between Pitches Meyer demonstrated that the deviations in ex- (Intervals) pectations arouse emotions when listening to music (Meyer, 1956). This concept is based on Dewey’s In music, patterns consisting of pitches are important. theory, according to which conflict causes emotions These patterns are explained in musical theories of (Dewey, 1894). The deviation from the listeners’ ex- temperament (how to determine the frequency of each pectation when listening to music arises from a par- note) and mode (which notes to use). The value of tial or complete disregard of rules that were accepted a pitch depends on the vibrational frequency of air. in advance. This indicates an increase in contingency Real sound consists of multiple frequencies, and we because of augmented uncertainties. These uncertain- perceive the lowest frequency as the pitch, also called ties present a commonality with complexity in the as the fundamental frequency. As with rhythm, the optimal complexity model (Berlyne, 1971) that illus- patterns of two pitches are called musical intervals, trates the relationship between complexity and hedo- 308 Development of Agents for Creating Melodies and Investigation of Interaction between the Agents nic values (Figure 3). This commonality suggests the culate the next note with probability density func- existence of a relationship between uncertainty and tions. In the next section, we describe how the agent emotion. Comparing sounds in our everyday life and selects the next note with probability density func- their relationships reveals interesting viewpoints. We tions. shall survey the points in Figure 3. At Position 1 , the complexity is relatively low. A listener can easily pre- dict the features of the sound, and a prediction event 3 AN AGENT CREATING is likely to arise in the proposed system. For example, the pure tick-tock beat of a clock not only sounds bor- MELODIES ing, but also causes displeasure in listeners. Indeed, some clock users cannot sleep with this sound. Po- To create a melody, the proposed agent selects a sound sition 2 has a higher complexity than Position 1 , timing, and subsequently selects a pitch. These ac- thus eliciting pleasure in the listener. The listener tions are based on the relationships as shown in 2.2 can predict the next sound, and recognize both real- and 2.3. The selections depend on the probabilities izations and deviations from expectation at that posi- that are built on the theory of musical expectation. In tion. Listeners may regard sounds as musical, because this section, we introduce the theory of musical ex- the sounds comprise rules as well as deviations from pectation, and explain an agent-creating melody. the rules at this position. Different levels of complex- ity exist in each musical genre. Rhythms, children’s 3.1 Lattice Spaces with Duple and songs, and folk songs have lower complexities than Triple Relationships pop music, for example. Therefore, a wide range of sounds are under this position. Position 3 exhibits an We provide a lattice space for rhythm that consists of appreciably high complexity.
Load more

Recommended publications
  • GRAMMAR of SOLRESOL Or the Universal Language of François SUDRE
    GRAMMAR OF SOLRESOL or the Universal Language of François SUDRE by BOLESLAS GAJEWSKI, Professor [M. Vincent GAJEWSKI, professor, d. Paris in 1881, is the father of the author of this Grammar. He was for thirty years the president of the Central committee for the study and advancement of Solresol, a committee founded in Paris in 1869 by Madame SUDRE, widow of the Inventor.] [This edition from taken from: Copyright © 1997, Stephen L. Rice, Last update: Nov. 19, 1997 URL: http://www2.polarnet.com/~srice/solresol/sorsoeng.htm Edits in [brackets], as well as chapter headings and formatting by Doug Bigham, 2005, for LIN 312.] I. Introduction II. General concepts of solresol III. Words of one [and two] syllable[s] IV. Suppression of synonyms V. Reversed meanings VI. Important note VII. Word groups VIII. Classification of ideas: 1º simple notes IX. Classification of ideas: 2º repeated notes X. Genders XI. Numbers XII. Parts of speech XIII. Number of words XIV. Separation of homonyms XV. Verbs XVI. Subjunctive XVII. Passive verbs XVIII. Reflexive verbs XIX. Impersonal verbs XX. Interrogation and negation XXI. Syntax XXII. Fasi, sifa XXIII. Partitive XXIV. Different kinds of writing XXV. Different ways of communicating XXVI. Brief extract from the dictionary I. Introduction In all the business of life, people must understand one another. But how is it possible to understand foreigners, when there are around three thousand different languages spoken on earth? For everyone's sake, to facilitate travel and international relations, and to promote the progress of beneficial science, a language is needed that is easy, shared by all peoples, and capable of serving as a means of interpretation in all countries.
    [Show full text]
  • 10 - Pathways to Harmony, Chapter 1
    Pathways to Harmony, Chapter 1. The Keyboard and Treble Clef Chapter 2. Bass Clef In this chapter you will: 1.Write bass clefs 2. Write some low notes 3. Match low notes on the keyboard with notes on the staff 4. Write eighth notes 5. Identify notes on ledger lines 6. Identify sharps and flats on the keyboard 7.Write sharps and flats on the staff 8. Write enharmonic equivalents date: 2.1 Write bass clefs • The symbol at the beginning of the above staff, , is an F or bass clef. • The F or bass clef says that the fourth line of the staff is the F below the piano’s middle C. This clef is used to write low notes. DRAW five bass clefs. After each clef, which itself includes two dots, put another dot on the F line. © Gilbert DeBenedetti - 10 - www.gmajormusictheory.org Pathways to Harmony, Chapter 1. The Keyboard and Treble Clef 2.2 Write some low notes •The notes on the spaces of a staff with bass clef starting from the bottom space are: A, C, E and G as in All Cows Eat Grass. •The notes on the lines of a staff with bass clef starting from the bottom line are: G, B, D, F and A as in Good Boys Do Fine Always. 1. IDENTIFY the notes in the song “This Old Man.” PLAY it. 2. WRITE the notes and bass clefs for the song, “Go Tell Aunt Rhodie” Q = quarter note H = half note W = whole note © Gilbert DeBenedetti - 11 - www.gmajormusictheory.org Pathways to Harmony, Chapter 1.
    [Show full text]
  • Introduction to Music Theory
    Introduction to Music Theory This pdf is a good starting point for those who are unfamiliar with some of the key ​ concepts of music theory. Reading musical notation Musical notation (also called a score) is a visual representation of the pitched notes ​ ​ heard in a piece of music represented by dots over a set of horizontal staves. In the top ​ ​ example the symbol to the left of the notes is called a treble clef and in the bottom ​ ​ example is called a bass clef. ​ ​ People often like to use a mnemonic to help remember the order of notes on each clef, ​ ​ here is an example. ​ Intervals An interval is the difference in pitch between two notes as defined by the distance ​ ​ ​ between the two notes. The easiest way to visualise this distance is by thinking of the notes on a piano keyboard. For example, on a C major scale, the interval from C to E is ​ ​ a 3rd and the interval from C to G is a 5th. Click here for some more interval examples. ​ ​ It is also common for an increase by one interval to be called a half­step, or ​ ​ ​ ​ semi­tone, and an increase by two intervals to be called a whole step, or tone. ​ ​ ​ ​ ​ ​ ​ Joe Rees­Jones, University of York, Department of Electronics 19/08/2016 Major and minor scales A scale is a set of notes from which melodies and harmonies are constructed. There are two main subgroups of scales: Major and minor. The type of scale is dependant on the ​ ​ ​ ​ intervals between the notes: Major scale ­ Tone, Tone, Semi­tone, Tone, Tone, Tone, Semi­tone ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ Minor scale ­ Tone, Semi­tone, Tone, Tone, Semi­tone, Tone, Tone ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ For example (by visualising a keyboard) the notes in C Major are: CDEFGAB, and C Minor are: CDE♭FGA♭B♭.
    [Show full text]
  • Major and Minor Scales Half and Whole Steps
    Dr. Barbara Murphy University of Tennessee School of Music MAJOR AND MINOR SCALES HALF AND WHOLE STEPS: half-step - two keys (and therefore notes/pitches) that are adjacent on the piano keyboard whole-step - two keys (and therefore notes/pitches) that have another key in between chromatic half-step -- a half step written as two of the same note with different accidentals (e.g., F-F#) diatonic half-step -- a half step that uses two different note names (e.g., F#-G) chromatic half step diatonic half step SCALES: A scale is a stepwise arrangement of notes/pitches contained within an octave. Major and minor scales contain seven notes or scale degrees. A scale degree is designated by an Arabic numeral with a cap (^) which indicate the position of the note within the scale. Each scale degree has a name and solfege syllable: SCALE DEGREE NAME SOLFEGE 1 tonic do 2 supertonic re 3 mediant mi 4 subdominant fa 5 dominant sol 6 submediant la 7 leading tone ti MAJOR SCALES: A major scale is a scale that has half steps (H) between scale degrees 3-4 and 7-8 and whole steps between all other pairs of notes. 1 2 3 4 5 6 7 8 W W H W W W H TETRACHORDS: A tetrachord is a group of four notes in a scale. There are two tetrachords in the major scale, each with the same order half- and whole-steps (W-W-H). Therefore, a tetrachord consisting of W-W-H can be the top tetrachord or the bottom tetrachord of a major scale.
    [Show full text]
  • Music Is Made up of Many Different Things Called Elements. They Are the “I Feel Like My Kind Building Bricks of Music
    SECONDARY/KEY STAGE 3 MUSIC – BUILDING BRICKS 5 MINUTES READING #1 Music is made up of many different things called elements. They are the “I feel like my kind building bricks of music. When you compose a piece of music, you use the of music is a big pot elements of music to build it, just like a builder uses bricks to build a house. If of different spices. the piece of music is to sound right, then you have to use the elements of It’s a soup with all kinds of ingredients music correctly. in it.” - Abigail Washburn What are the Elements of Music? PITCH means the highness or lowness of the sound. Some pieces need high sounds and some need low, deep sounds. Some have sounds that are in the middle. Most pieces use a mixture of pitches. TEMPO means the fastness or slowness of the music. Sometimes this is called the speed or pace of the music. A piece might be at a moderate tempo, or even change its tempo part-way through. DYNAMICS means the loudness or softness of the music. Sometimes this is called the volume. Music often changes volume gradually, and goes from loud to soft or soft to loud. Questions to think about: 1. Think about your DURATION means the length of each sound. Some sounds or notes are long, favourite piece of some are short. Sometimes composers combine long sounds with short music – it could be a song or a piece of sounds to get a good effect. instrumental music. How have the TEXTURE – if all the instruments are playing at once, the texture is thick.
    [Show full text]
  • Tools-For-Tosafos-Selections.Pdf
    wffiffiLs FOR w &F F$af,m Per$mutter T.AR G UI\,{,/F.E LD }-{ ts N N4 $sltroducttost Whot trs Tosef'os? Tosafos is a collection of the interpretations and explana- tions of the Gemara by the group of sages known as "baalei haTosdos," i.e., the Tosafos masters. Tt:re baalei haTosafos (also known as "Tosafists") were sages of theJewish communities in France and Germany (with a few in other European countries) in the twelfth and thirteenth centuries. Some of them offici- ated as the halachic leaders of the community and functioned as representatives to the gentile authorities. Some ranyeshivos, where disciples would devote all their time to studying Torah. ThebaaleihaTosafoslived in a time that is regarded inJewish history as the period of the Rishonim. "Rishonirn" (literally "first") is the collective term given to the sages who lived in Europe and North Africa after the time of the Geonim (who lived in Babylon). This period extended until the Tur or R' Yosef Karo (who compiled the Shulchan Aruch), after which the period of the Acharonim began. Not all the sages who lived in these areas during this time period are called Tosafists, however. The term "Tosafist" applies to those who learned the Gemara in a certain way. The way th,e baalei haTosafos learned is, in effect, the focus of this work. 1Z Tools for Tosafos Introrttacn-ion 13 a sage who constantly compated At this poin! we can say that Sirece then, mrost prlntirags of the Taknud have contained differences in the Talmudic text, -W?t-{sa'l'{ and attempted to consolidate Tcsafcs's c*lrlmentar)'.
    [Show full text]
  • The Chromatic Scale
    Getting to Know Your Guitar: The Chromatic Scale Your Guitar is designed as a chromatic instrument – that is, guitar frets represent chromatic “semi- tones” or “half-steps” up and down the guitar fretboard. This enables you to play scales and chords in any key, and handle pretty much any music that comes from the musical traditions of the Western world. In this sense, the chromatic scale is more foundational than it is useful as a soloing tool. Put another way, almost all of the music you will ever play will be made interesting not by the use of the chromatic scale, but by the absence of many of the notes of the chromatic scale! All keys, chords, scales, melodies and harmonies, could be seen simply the chromatic scale minus some notes. For all the examples that follow, play up and down (both ascending and descending) the fretboard. Here is what you need to know in order to understand The Chromatic Scale: 1) The musical alphabet contains 7 letters: A, B, C, D, E, F, G. The notes that are represented by those 7 letters we will call the “Natural” notes 2) There are other notes in-between the 7 natural notes that we’ll call “Accidental” notes. They are formed by taking one of the natural notes and either raising its pitch up, or lowering its pitch down. When we raise a note up, we call it “Sharp” and use the symbol “#” after the note name. So, if you see D#, say “D sharp”. When we lower the note, we call it “Flat” and use the symbol “b” after the note.
    [Show full text]
  • Chromatic Fingering Chart for Euphonium T.C
    Chromatic Fingering Chart for Euphonium T.C. Note: Only the most commonly used fingerings are listed here, in order of preference. The overtone chart available on this website provides comprehensive information about available alternate fingerings. The differing fingerings for certain lower-register notes on compensating versus non-compensating instruments are clearly indicated. All sounding pitches are a major ninth lower than written. G-Sharp or A-Flat A-Sharp or B-Flat G (Concert F) A (Concert G) B (Concert A) C (Concert B-Flat) (Concert F-Sharp or G-Flat) (Concert G-Sharp or A-Flat) & w #w bw w #w bw w w Ÿ ◊ 1 (false tone) 2 (false tone) 2-4 (false tone) 4 (false tone) 2-3 (false tone) 1-2 (false tone) 1-2-3 (false tone) 1-3 (false tone) C-Sharp or D-Flat D-Sharp or E-Flat F-Sharp or G-Flat (Concert B or C-Flat) D (Concert C) (Concert C-Sharp or D-Flat) E (Concert D) F (Concert E-Flat) (Concert E or F-Flat) & #w bw w #w bw w w #w bw “C‘ompensating: Compensating: Compensating: Compensating: Compensating: 2-4 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 1-2-3 Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: 1-2-3-4 (false tone) 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 G-Sharp or A-Flat A-Sharp or B-Flat G (Concert F) A (Concert G) B (Concert A) C (Concert B-Flat) (Concert F-Sharp or G-Flat) (Concert G-Sharp or A-Flat) & w #w bw w #w bw w w “4‘ 2-3 1-2 1 2 0 1-3 3 C-Sharp or D-Flat D-Sharp or E-Flat F-Sharp or G-Flat (Concert B or C-Flat) D (Concert C) (Concert C-Sharp or D-Flat) E (Concert D) F (Concert E-Flat) (Concert E or F-Flat) & bw #w bw w #w bw w w #w2-4 Compensating: Compensating: Compensating: Compensating: Compensating: 1-2-3 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: 1-2-3-4 (false tone) 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 G-Sharp or A-Flat A-Sharp or B-Flat G (Concert F) A (Concert G) B (Concert A) C (Concert B-Flat) (Concert F-Sharp or G-Flat) (Concert G-Sharp or A-Flat) & bw w w w4 #w2-3 bw w1-2 #w1 2 0 1-3 3 1-4 2 Chromatic Fingering Chart for Euphonium T.C.
    [Show full text]
  • In Search of the Perfect Musical Scale
    In Search of the Perfect Musical Scale J. N. Hooker Carnegie Mellon University, Pittsburgh, USA [email protected] May 2017 Abstract We analyze results of a search for alternative musical scales that share the main advantages of classical scales: pitch frequencies that bear simple ratios to each other, and multiple keys based on an un- derlying chromatic scale with tempered tuning. The search is based on combinatorics and a constraint programming model that assigns frequency ratios to intervals. We find that certain 11-note scales on a 19-note chromatic stand out as superior to all others. These scales enjoy harmonic and structural possibilities that go significantly beyond what is available in classical scales and therefore provide a possible medium for innovative musical composition. 1 Introduction The classical major and minor scales of Western music have two attractive characteristics: pitch frequencies that bear simple ratios to each other, and multiple keys based on an underlying chromatic scale with tempered tuning. Simple ratios allow for rich and intelligible harmonies, while multiple keys greatly expand possibilities for complex musical structure. While these tra- ditional scales have provided the basis for a fabulous outpouring of musical creativity over several centuries, one might ask whether they provide the natural or inevitable framework for music. Perhaps there are alternative scales with the same favorable characteristics|simple ratios and multiple keys|that could unleash even greater creativity. This paper summarizes the results of a recent study [8] that undertook a systematic search for musically appealing alternative scales. The search 1 restricts itself to diatonic scales, whose adjacent notes are separated by a whole tone or semitone.
    [Show full text]
  • A History of Mandolin Construction
    1 - Mandolin History Chapter 1 - A History of Mandolin Construction here is a considerable amount written about the history of the mandolin, but littleT that looks at the way the instrument e marvellous has been built, rather than how it has been 16 string ullinger played, across the 300 years or so of its mandolin from 1925 existence. photo courtesy of ose interested in the classical mandolin ony ingham, ondon have tended to concentrate on the European bowlback mandolin with scant regard to the past century of American carved instruments. Similarly many American writers don’t pay great attention to anything that happened before Orville Gibson, so this introductory chapter is an attempt to give equal weight to developments on both sides of the Atlantic and to see the story of the mandolin as one of continuing evolution with the odd revolutionary change along the way. e history of the mandolin is not of a straightforward, lineal development, but one which intertwines with the stories of guitars, lutes and other stringed instruments over the past 1000 years. e formal, musicological definition of a (usually called the Neapolitan mandolin); mandolin is that of a chordophone of the instruments with a flat soundboard and short-necked lute family with four double back (sometimes known as a Portuguese courses of metal strings tuned g’-d’-a”-e”. style); and those with a carved soundboard ese are fixed to the end of the body using and back as developed by the Gibson a floating bridge and with a string length of company a century ago.
    [Show full text]
  • Natural Minor Scale Is Given
    Minor Scales Minor scales/keys are used by composers when they wish to express a different mood than those characterized my major scales in music. Minor scales and keys conjure feelings of sorrow or tension. Minor scales also have their own unique set of intervals found between the 8 pitches in the scale. The major scale which used all white notes on the piano is the C major scale (example #1). Example #1 q Q Q l=============& _q q q q l q =l[ The minor scale which uses all white notes on the piano the scale with no sharps or flats is A minor. The C major scale and the A minor scale are related (they are cousins) because they share the same key signature, no sharps or flats. Example #2 shows that relationship very clearly. All of notes in the A minor scale are found in the C major scale with the difference between the two just the starting note or tonic. The C major scale starts on C which is its tonic and the A minor scale starts on A which is its tonic. Example #2 Î Î q Q Q Major l===============& _q q lq q q l =l[ l l q q q Î Î Minor l===============& _q _q _q q l q l =l[ The unique relationship of major and minor makes the work of studying minor simpler. As we know from the information above each major scale/key has a relative (cousin) minor that uses the same notes and key signatures however each starts on a different note (tonic).
    [Show full text]
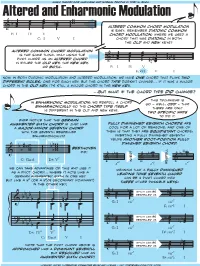
  • Altered and Enharmonic Modulation
    Altered andmusic Enharmonictheory for musicians and normal people Modulation by toby w. rush œ œ w b œ œ œ nœ w Altered common chord modulation & œ œ is easy: remember diatonic common F: I IV V chord modulation, where we used a C: I V I chord that was diatonic in both the old and new keys? altered common chord modulation is the same thing, only using the œ œ pivot chord as an altered chord & b œ œ œ #nw in either the old key, the new key, œ # #œ w or both. F: I IV V n œ E: bVI V I Now, in both diatonic modulation and altered modulation, we have one chord that plays two different roles, one for each key. But the chord type doesn’t change... if it was a major chord in the old key, it’s still a major chord in the new key. ...but...but whatwhat ifif thethe chordchord typetype did change? this technique is in enharmonic modulation, we respell a chord so — well, odd — that so the enharmonically chord type itself there are only is different in the old and new keys. two specific ways to do it. ever notice that the german augmented sixth chord is just like fully diminished seventh chords are a major-minor seventh chord cool for a lot of reasons, and one of with the seventh respelled them is that they are equidistant chords: enharmonically? inverting a fully diminshed seventh yields another root-position fully dimished seventh chord. # w bw beethoven b ww b w did! & b w bw bw bww b ∫w 7 b w C: Ger.6 D : V b w b w w b & w7 invert & 6 & 7 a° a°5 respell c° we can take advantage of this and use it meaning that a fully diminished as a pivot chord..
    [Show full text]