Time Series Analysis of Hemorrhagic Fever with Renal Syndrome: a Case Study in Jiaonan County, China
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
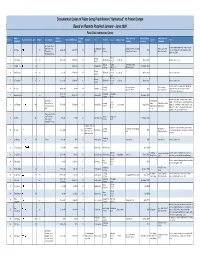
Documented Cases of Falun Gong Practitioners "Sentenced" to Prison Camps Based on Reports Received January - June 2009 Falun Dafa Information Center
Documented Cases of Falun Gong Practitioners "Sentenced" to Prison Camps Based on Reports Received January - June 2009 Falun Dafa Information Center Name Date of Sentence Place currently Scheduled date Initial place of Case # Name (Chinese) Age Gender Occupation Date of Sentencing Charges City Province Court Judge's name Lawyer Notes (Pinyin)2 Detention length detained of release detention Employee of No.8 Arrested with his wife at his mother-in-law's Mine of the Coal Pingdingshan Henan Zhengzhou Prison in Xinmi Pingdingshan City 1 Liu Gang 刘刚 m 18-May-08 early 2009 18 2027 home; transferred to current prison around Corporation of City Province City, Henan Province Detention Center March 18, 2009 Pingdingshan City Nong'an Nong'an 2 Wei Cheng 魏成 37 m 27-Sep-07 27-Mar-09 18 Jilin Province Guo Qingxi March, 2027 Arrested from home; County County Court Zhejiang Fuyang Zhejiang Province 3 Jin Meihua 金美华 47 f 19-Nov-08 15 Fuyang City November, 2023 Province City Court Women's Prison Nong'an Nong'an 4 Han Xixiang 韩希祥 42 m Sep-07 27-Mar-09 14 Jilin Province County Guo Qingxi March, 2023 Arrested from home; County Court Nong'an Nong'an 5 Li Fengming 李凤明 45 m 27-Sep-07 27-Mar-09 14 Jilin Province County Guo Qingxi March, 2023 Arrested from home; County Court Arrested from home; detained until late April Liaoning Liaoning Province Fushun Nangou 6 Qi Huishu 齐会书 f 24-May-08 Apr-09 14 Fushun City 2023 2009, and then sentenced in secret and Province Women's Prison Detention Center transferred to current prison. -

Tone Sandhi in Jiaonan Dialect: an Optimality Theoretical Account
TAL 2012 ̶ Third International ISCA Archive Symposium on Tonal Aspects of http://www.isca-speech.org/archive Languages Nanjing, China, May 26-29, 2012 Tone Sandhi in Jiaonan Dialect: an Optimality Theoretical Account Zhao Cunhua 1, Zhai Honghua 2 1 College of Foreign Languages, Shandong University of Science and Technology, China 2 College of Foreign Languages, Shandong University of Science and Technology, China [email protected], [email protected] Abstract 2. Experimental Description Based on phonetic experiment, this paper aims at providing The raw phonetic data is gained through the acoustic records phonetic description on the tones and disyllabic tone sandhi in conducted in July 2009 and November 2010 respectively. Jiaonan dialect, and then illustrating the phonological Only one elder male’s and female’s sound were chosen from structures within the framework of Auto-segmental Phonology the six informants’ invited in 2009. The test words were from to conduct an OT analysis on the tone sandhi patterns of Fangyan Diaocha Zibiao and The Study of Shandong Dialect, Jiaonan dialect. including 160 monosyllabic words in citation forms and 130 Index Terms: Jiaonan dialect, phonetics, tone, tone sandhi, pairs in disyllabic sequences. Finally, 111 monosyllabic words OT in citation forms and 117 in disyllabic sequences are involved and taken for the next recording. The equipment used then 1. Introduction was SAMSUNG BR-1640 digital recorder. In 2011, 6 college Jiaonan, a county-level city of Qingdao, locates in the students from Jiaonan City were invited for audio recording. southeast of Shandong Peninsula. Jiaonan dialect (JND for Data recording was made by using a portable computer short hereafter) belongs to Jiao Liao Mandarin, a sub-dialect (Lenovo) and a microphone (Sennheiser PC 166) with the of the northern Mandarin family. -

Vertical Distribution and Settling Process of Pb in Jiaozhou Bay
2nd International Workshop on Materials Engineering and Computer Sciences (IWMECS 2015) Vertical distribution and settling process of Pb in Jiaozhou bay Dongfang Yang1,2,3,a, Fengyou Wang1,2, Xiuqin Yang1,2, Yunjie Wu1,2,b and Sixi 1,2 Zhu 1Research Center for Karst Wetland Ecology, Guizhou Minzu University, Guizhou Guiyang, Guizhou Guiyang, China; 2College of Chemistry and Environmental Science, Guizhou Minzu University, Shanghai, 550025, China; 3North China Sea Environmental Monitoring Center, SOA, Qingdao 266033, China. [email protected]; bCorresponding author:[email protected]. Keywords: Pb; Vertical; Horizontal; Seasonal; Distribution; Settling process; Jiaozhou Bay Abstract. Based on the investigation data on Pb in Jiaozhou Bay in May, September and October in 1983, were analyzed the horizontal and seasonal distribution of Pb. The results in this paper showed that Pb contents in surface and bottom waters were closed in the bay mouth in different seasons. For seasonal distributions, Pb contents in surface waters were in order of Summer > Autumn > Spring, while for bottom waters were in order of Autumn > Summer > Spring. In the bay mouth waters, in the temporal scale, the seasonal change order of the Pb content from the high value to the low in the surface waters was summer, autumn and spring, it in the bottom was autumn, summer and spring. The horizontal distributions of Pb in surface and bottom waters were consistent in waters inside the bay in May, while in waters outside the bay in September and October were inverse. The vertical distribution and seasonal change of Pb in the Jiaozhou Bay waters unveiled the settling process of Pb in waters. -

Own-Brand Food, Homewares, Health and Beauty
Total Number % of Female % of Male Worker Buying Group ZS Number Site name Address Country of Workers Workers Workers Representation Morrisons Food ZS1000075 Single Source Stafford Park 6, Telford, TF3 3AT United Kingdom 120 58% 42% Yes Morrisons Food ZS1000097 Huegli UK Ltd Oxleasow Road, Redditch, B98 0RE United Kingdom 99 51% 49% Yes Morrisons Food ZS1000985 Oakham Ales - Maxwell Road Maxwell Road, Woodston, Peterborough, PE2 7JB United Kingdom 40 23% 78% No Morrisons Food ZS1000990 Fromageries Papillon Impasse de la Route de Tiergues, Lauras, Roquefort Sur Soulzon, 12250 France 83 48% 52% Yes Morrisons Food ZS1001380 Mademoiselle Desserts - Valade Lieu Dit Valade, Condat Sur Trincou, 24530 France 500 46% 54% Yes Morrisons Non-Food ZS1001455 Kim Duc Vinh Loc 2 Industrial Zone, Long Hiep Commune, Ben Luc District, Long An Province, 850000 Vietnam 800 60% 40% Yes Morrisons Food ZS1001947 Alimentos Sumar S.A. - El Tejar Carretera Interamericana, El Tejar, 1 Guatemala 230 65% 35% No Morrisons Food ZS1002139 Konspol Bis Poznańska Street, Slupca, 62-400 Poland 939 59% 41% Yes Morrisons Food ZS1002164 Place UK Ltd Church Farm, Tunstead, Norwich, NR12 8RQ United Kingdom 577 38% 62% Yes Morrisons Food ZS1002170 TH21 - Minburi Suwinthawong Rd, Sansab, Minburi, Bangkok, 10510 Thailand 1360 61% 39% No Morrisons Food ZS1002195 Baronie UK Darwin Road, Willowbrook Industrial Estate, Corby, NN17 5XZ United Kingdom 136 54% 46% Yes Morrisons Food ZS1002269 Valeo Confectionary - Liverpool Beech Street, Liverpool, L7 0HA United Kingdom 184 41% 59% Yes -

The Influences of Precipitation on Cr in Jiaozhou Bay
2019 International Conference on Civil Engineering, Materials and Environment (ICCEME 2019) The influences of precipitation on Cr in Jiaozhou Bay Dongfang Yang1, 2, 3, a, Zhenqing Miao4, b,c, Haixia Li1,2, Jun Ding1,2, Qi Wang1 1Center for Accounting and Auditing Informatics, Xijing University, Xian 710123, China; 2Accountancy Shool, Xijing University, Xian 710123, China; 3North China Sea Environmental Monitoring Center, SOA, Qingdao 266033, China 4College of Fisheries, Zhejiang Ocean University, Zhoushan, 316022, China. Keywords: Cr; Precipitation; Seasonal variation; Point source; Non-point source; Jiaozhou Bay. Abstract: Understanding the seasonal variations of Cr pollution and pollution source is essential to pollution control and environmental remediation. Jiaozhou Bay is a semi-closed bay located in Shandong Province, China. This paper analyzed the seasonal variations of Cr and precipitation in Jiaozhou Bay in 1979-1983. Results showed that Cr contents in Jiaozhou Bay were showing high seasonal variations and were in order of spring > summer, yet the precipitation in Jiaozhou Bay was in order of summer > spring. Cr contents in Jiaozhou Bay were not only determined by precipitation or stream flow, since Cr inputs to Jiaozhou Bay were generated from both point and non-point sources, and the corresponding source control countermeasures were necessary. 1. Introduction Cr had been widely used in various industries, and many bays have been polluted by Cr [1-4]. Jiaozhou Bay is a semi-closed bay located in Shandong Province, eastern China, and has been polluted by various pollutants including Cr [5-8]. Hence, Understanding the seasonal variations of Cr pollution and pollution source is essential to pollution control and environmental remediation. -
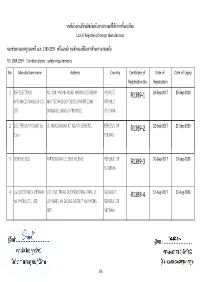
No. Manufacture Name Address Country Certificate of Registration
รายชื่อโรงงานที่ทําผลิตภัณฑ์ในต่างประเทศที่ได้รับการขึ้นทะเบียน List of Registered Foreign Manufacturer ขอบข่ายตามมาตรฐานเลขที่ มอก. 1389-2559 เครื่องอบผ้า คุณลักษณะที่ต้องการด้านความปลอดภัย TIS 1389-2559 : Tumbler dryers : safety requirements No. Manufacture name Address Country Certificate of Date of Date of Expiry Registration No. Registration 1 BSH ELECTRICAL NO. 208, YAOXIN ROAD, NANJING ECONOMY PEOPLE'S R1389-1 26-Sep-2017 25-Sep-2020 APPLIANCES (JIANGSU) CO., AND TECHNOLOGY DEVELOPMENT ZONE REPUBLIC LTD (XINGANG), JIANGSU PROVINCE, OF CHINA 2 ELECTROLUX POLAND Sp. UL WARSZAWSKA 87, 42-470 SIEWIERZ, REPUBLIC OF R1389-2 22-Sep-2017 21-Sep-2020 Z.o.o POLAND 3 GORENJE, D.D. PARTIZANSKA 12, 3503 VELENJE, REPUBLIC OF R1389-3 20-Sep-2017 19-Sep-2020 SLOVENIA 4 LG ELECTRONICS VIETNAM LOT CN2, TRANG DUE INDUSTRIAL PARK, LE SOCIALIST R1389-4 31-Aug-2017 30-Aug-2020 HAI PHONG CO., LTD. LOI WARD, AN DUONG DISTRICT HAI PHONG REPUBLIC OF CITY VIETNAM 1/6 รายชื่อโรงงานที่ทําผลิตภัณฑ์ในต่างประเทศที่ได้รับการขึ้นทะเบียน List of Registered Foreign Manufacturer ขอบข่ายตามมาตรฐานเลขที่ มอก. 1389-2559 เครื่องอบผ้า คุณลักษณะที่ต้องการด้านความปลอดภัย TIS 1389-2559 : Tumbler dryers : safety requirements No. Manufacture name Address Country Certificate of Date of Date of Expiry Registration No. Registration 5 SAMSUNG ELECTRONICS 107, HANAMSANDAN 6 BEON-RO, REPUBLIC OF R1389-6 19-Sep-2017 18-Sep-2020 CO., LTD. GWANGSAN-GU, GWANGJU KOREA 6 SAMSUNG ELECTRONICS LOT I-11, D2 ROAD, SAIGON HI-TECH PARK REPUBLIC OF R1389-7 22-Sep-2017 21-Sep-2020 HCMC CE COMPLEX CO., TANG NHON PHU B WARD DISTRICT 9, HO VIETNAM LTD. CHI MINH CITY, 7 SUZHOU SAMSUNG NO. 501, SUHONG EAST ROAD, SUZHOU PEOPLE'S R1389-8 14-Sep-2017 13-Sep-2020 ELECTRONICS CO., LTD. -

Qingdao Facts
QINGDAO CHINA EXPAT GUIDE Qingdao Facts Geographic Location & Climate Qingdao is located in the middle of Shandong Peninsula (120°22′E, 36°4′N), with the Yellow Sea to the east and south, and the mainland to the west and north. Qingdao covers an area of 10,654sq km. Located in the temperate semi-humid continental climate zone, it is a well-known summer resort. The average summer and winter temperatures are 25 and 1.3 respectively with an annual average temperature of 12.2 . Average annual rainfall is 775.6 mm. ℃ ℃ ℃ Districts, Counties, and Population Qingdao is comprised of 7 districts: Shinan, Shibei, Sifang, Licang, Chengyang, Huangdao, and Laoshan, and 5 county-level cities: Jiaozhou, Jiaonan, Jimo, Pingdu, and L a i x i. The total population of approximately 8.2 million comes under the jurisdiction of Qingdao Local Government. The urban population is 2.3 million which includes 60,000 Koreans working and/or residing in Qingdao. Getting Here and Away Liuting International Airport: Qingdao currently offers 19 international & interregional passenger and freight air routes, with over 300 flights per week. Qingdao's International Airport (TAO) offers direct flights to Tokyo, Osaka, Fukuoka, Seoul, Busan, Taegu, Paris, Singapore, Bangkok, Hong Kong, and Macao with a new route to Frankfurt currently underway. Qingdao's airport also provides over 800 domestic flights per week, directly linking Qingdao with 47 cities including Beijing, Shanghai, Guangzhou. Flight Times to Adjacent Cities: Seoul: 1 hour Busan: 1 hour 30 min. Fukuoka: 1 hour 30 min. Tokyo: 2 hours 40 min. Osaka: 2 hours Beijing: 1 hour Shanghai: 1 hour Guangzhou: 2.5 Railway, Highway Networks, Bus & Ferry Terminals The Qingdao Railway Station provides frequent connections to regions throughout China with direct routes to Beijing, Shanghai, Jinan, Weihai, and Yantai (just to name a few). -

Download Article (PDF)
2nd International Conference on Machinery, Materials Engineering, Chemical Engineering and Biotechnology (MMECEB 2015) Vertical variation and migration of Pb in Jiaozhou Bay waters Dongfang Yang1,2,4,a, Sixi Zhu1,2, Danfeng Yang3, Fengyou Wang1,2,b,c and 1,2 Yunjie Wu 1Research Center for Karst Wetland Ecology, Guizhou Minzu University, Guizhou Guiyang, Guizhou Guiyang, China; 2College of Chemistry and Environmental Science, Guizhou Minzu University, Shanghai, 550025, China; 3College of Information Science and Engineering, Fudan University, Shanghai, 200433, China; 4North China Sea Environmental Monitoring Center, SOA, Qingdao 266033, China. [email protected]; bCorresponding author: [email protected] Keywords: Pb; Seasonal variation; Vertical variation; Settling process; Jiaozhou Bay Abstract. Based on the investigation data on Pb in waters in 1984, were analyzed the horizontal distribution, seasonal variation and settling process of Pb in water in the bay mouth of Jiaozhou Bay, eastern China. Results showed that the seasonal variations of Pb contents in surface waters and bottom waters were consist, and were in order of summer > autumn. In spatial scale, the migration and sedimentation distances of Pb were determined bay Pb contents in waters, and the spatial sedimentaion processes could be revealed by the horizontal distributions of Pb. In vertical scale, Pb contents in surface and bottom waters were closed in cased of low Pb contents in waters, while in case of high Pb contents in waters the differences of Pb contents in surface and bottom waters were relative high. In generally, the seasonal variations and vertical distributions of Pb in waters were indicating the horizontal water’s effect and vetical water’s effect, and were reveal the horizontal migration and horizontal sedimentation processes of Pb. -

Establishment of the Ecosystem-Based Integrated Monitoring System of Jiaozhou Bay: Discussion on the Mode of Public Participation
Demonstration Zone of Integrated Ecosystem-based Investigation on Wetland of Jiaozhou Bay of Qingdao (UNDP/GEF YSLME Phase II Project) Establishment of the Ecosystem-based Integrated Monitoring System of Jiaozhou bay: Discussion on the mode of Public Participation Zijun Xu, Qi Zhang, Fei Teng, Yanping Qi, Ying Wang North China Sea Environmental Monitoring Center, SOA June 2020 Content PREFACE .................................................................................................. 1 1 INTRODUCTION OF JIAOZHOU BAY ........................................ 2 1.1 RECOURCES IN JIAOZHOU BAY ............................................................ 3 1.2 MARINE ENVIRONMENT OF JIAOZHOU BAY ....................................... 11 1.3 THE PROBLEMS ON JIAOZHOU BAY ECOSYSTEM ................................ 12 2 ECOSYSTEM BASED INTEGRATED COASTAL MANAGEMENT OF JIAOZHOU BAY .............................................. 17 2.1 ECOSYSTEM BASED INTEGRATED COASTAL MANAGEMENT(ICM) ................................................................................................................ 17 2.2 THE MANAGEMENT STATUS OF JIAOZHOU BAY .................................. 18 2.3 THE CHANLLENGES TO MANANGEMENT JIAOZHOU BAY .................... 22 2.4 THE MECHANISM OF ECOSYSTEM-BASED INTEGRATED MANAGEMENT IN JIAOZHOU BAY .................................................................................... 23 3 ESTABLISHMENT OF ECOSYSTEM-BASED INTEGRATED MONITORING SYSTEM OF JIAOZHOU BAY ................................ 29 3.1 THE REQUIREMENTS -

中国(偶蹄類の加熱処理肉等) 2021/5/25通知 No. NAME
中国(偶蹄類の加熱処理肉等) 2021/5/25通知 No. NAME ADDRESS TEMPORARY HUANG GANG NO.670, SHUN HUANG ROAD, SUN HE 1100/03009 BEIJING HORMEL FOODS CO.,LTD. COUNTY, CHAOYANG DISTRICT, BEIJING, CHINA 1100/03015 BEIJING DAFA CHIA TAI CO.,LTD YANGZHEN DUZHUANG, SHUNYI DISTRICT, BEIJING CITY, CHINA 1100/03039 BEIJING JIAYI FOOD JOINT FACTORY XIAOTANGSHAN TOWN, CHANGPING DISTRICT, BEIJING BEIJING ER SHANG MOQI ZHONGHONG FOODS NO. 233 NANGAO VILLAGE CUIGEZHUANG TOWNSHIP CHAOYANG 1100/15006 CO.,LTD. DISTRICT BEIJING, CHINA 1200/01025 TIANJIN LINGCHUAN FOOD CO.,LTD XINKOU INDUSTRIAL ZONE BY ROAD NO.18, XIQING DISTRICT, TIANJIN TIANJIN 3RD FOOD PRODUCTS PROCESSING 1200/03001 HANJIASHU, BEICHEN DISTRICT, TIANJIN FACTORY 1200/03008 TIANJIN MEAT PRODUCTS PROCESSING COMPLEX NO.8, YUEJIN ROAD, DONGLI DISTRICT, TIANJIN NO.8 XINWANG ROAD, SHUANGQIAOHE TOWN, JINNAN DISTRICT, 1200/03009 TIANJIN DONGTIAN FOODS PROCESSING CO., LTD TIANJIN, CHINA TIANJIN TEDA TIANQUAN QUICK FROZEN 1200/29002 NO.11, JINGU ROAD, TANGGU DISTRICT, TIANJIN FOODSTUFFS CO.,LTD. 1200/29005 TIANJIN GUOSHI FOOD CO., LTD. LANGYUAN VILLAGE, BEICHEN DISTRICT, TIANJIN 1200/29012 TIANJIN SHIYOU FOODSTUFFS CO.,LTD. SICUNDIAN, WUQING COUNTY, TIANJIN 1200/29016 TIANJIN NICKY FOODSTUFFS CO., LTD. 13 STREET, EXPORT PROCESSING ZONE, TIANJIN NO.171, MUSLIM BUSINESS TRADE STREET, XIADIAN TOWN, DACHANG 1300/03105 HEBEI SUPERB FOODS CO., LTD HUI AUTONOMY COUNTY, HEBEI PROVINCE, CHINA KANGBAO BAILU MEAT CO., LTD. THE SECOND 1300/03152 NO.134, GONGYE STREET, KANGBAO COUNTY, HEBEI FACTORY NO.9 HEBIN ROAD, LUANPINGTOWN, LUANPING COUNTY, CHENGDE 1300/03158 LUANPING HUADU JIAYI FOOD JOINT FACTORY CITY, HEBEI PROVINCE SHIJIAZHUANG DEYUAN FOOD CO.,LTD. 1300/03160 NO.77, XINYUANXI ROAD, LUANCHENG DISTRICT, SHIJIAZHUANG, HEBEI LUANCHENG BRANCH 1300/08040 SHIJIAZHUANG HUIKANG FOOD CO.,LTD. -

Download Article (PDF)
2nd International Conference on Machinery, Materials Engineering, Chemical Engineering and Biotechnology (MMECEB 2015) High sedimentation rate region of Pb in Jiaozhou Bay Dongfang Yang1,2,3,a, Sixi Zhu1,2, Yunjie Wu1,2, Xiuqin Yang1,2 and Fengyou 1,2,b,c Wang 1Research Center for Karst Wetland Ecology, Guizhou Minzu University, Guizhou Guiyang, Guizhou Guiyang, China 2College of Chemistry and Environmental Science, Guizhou Minzu University, Guiyang, 550025, China 3North China Sea Environmental Monitoring Center, SOA, Qingdao 266033, China. [email protected]; bcorresponding author: [email protected]. Keywords: Pb; Bottom water; Water quality; Distribution; High sedimentation rate region; Jiaozhou Bay Abstract. Based on investigation dada on lead (Pb) in July and October 1984 in bottom waters in Jiaozhou Bay, we analyzed the content, pollution level and distribution of Pb. Results showed that Pb contents in 1984 in bottom waters were 1.33-17.34 μg L-1 and were meeting Grade II, III and IV in National Sea Water Quality Standard (GB 3097-1997). There were high sedimentation regions in different positions by means of vertical water’s effect. There was high sedimentation region in the outside of the bay mouth in July, while in October there was high sedimentation region in the bay mouth. Pb contents in waters and the vertical water’s effect was the major reason for the distributions of the water quality and sedimentation rates of Pb in Jiaozhou Bay. Introduction Pb has been widely used in industry and agriculture, and a large amount of Pb-containing waste waters were generated and discharged to rivers and marine bays along with the rapid increase of industry and agriculture [1-6]. -

The Consistency of Arsenic's High Value Regions in Surface and Bottom
E3S Web of Conferences 38, 01026 (2018) https://doi.org/10.1051/e3sconf/20183801026 ICEMEE 2018 The consistency of Arsenic’s high value regions in surface and bottom waters in Jiaozhou Bay Dongfang Yang1,2,3, *, Jianxun Chai1,2, Xiaoye Gao1,2, Yunjie Wu1,2, and Sixi Zhu1,2 1Research Center for Karst Wetland Ecology, Guizhou Minzu University, Guizhou Guiyang, Guizhou Guiyang, China 2College of Chemistry and Environmental Science, Guizhou Minzu University, Shanghai, 550025, China 3North China Sea Environmental Monitoring Center, SOA, Qingdao 266033, China Abstract. This paper analyzed the contents and distributions of As in Jiaozhou Bay in 1982. Results showed that As’s contents in bottom waters in coastal waters in the southwest of the bay and the bay mouth in Jiaozhou Bay in July and October 1982 were 0.88-4.48 μg L-1 and 0.84-1.16 μg L-1, respectively. As’s contents were much lower than the guide line of Grade I, and the pollution level of As in bottom waters in Jiaozhou Bay in 1982 was still very slight. There was high value region in coastal waters in the southwest of the bay in July 1982 (4.48 μg L-1), while in October 1982 high value region was in the bay mouth (1.16 μg L-1). The source input of As from overland runoff in the southwest was strong in July, resulted in relative high value region in surface waters in coastal waters in the southwest of the bay, and therefore resulted in high value region in bottom waters in same region by means of rapid sedimentation of As.