PDF and HTML
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
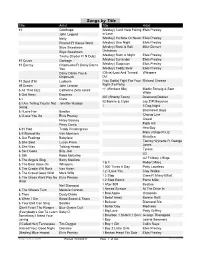
Songs by Title
Songs by Title Title Artist Title Artist #1 Goldfrapp (Medley) Can't Help Falling Elvis Presley John Legend In Love Nelly (Medley) It's Now Or Never Elvis Presley Pharrell Ft Kanye West (Medley) One Night Elvis Presley Skye Sweetnam (Medley) Rock & Roll Mike Denver Skye Sweetnam Christmas Tinchy Stryder Ft N Dubz (Medley) Such A Night Elvis Presley #1 Crush Garbage (Medley) Surrender Elvis Presley #1 Enemy Chipmunks Ft Daisy Dares (Medley) Suspicion Elvis Presley You (Medley) Teddy Bear Elvis Presley Daisy Dares You & (Olivia) Lost And Turned Whispers Chipmunk Out #1 Spot (TH) Ludacris (You Gotta) Fight For Your Richard Cheese #9 Dream John Lennon Right (To Party) & All That Jazz Catherine Zeta Jones +1 (Workout Mix) Martin Solveig & Sam White & Get Away Esquires 007 (Shanty Town) Desmond Dekker & I Ciara 03 Bonnie & Clyde Jay Z Ft Beyonce & I Am Telling You Im Not Jennifer Hudson Going 1 3 Dog Night & I Love Her Beatles Backstreet Boys & I Love You So Elvis Presley Chorus Line Hirley Bassey Creed Perry Como Faith Hill & If I Had Teddy Pendergrass HearSay & It Stoned Me Van Morrison Mary J Blige Ft U2 & Our Feelings Babyface Metallica & She Said Lucas Prata Tammy Wynette Ft George Jones & She Was Talking Heads Tyrese & So It Goes Billy Joel U2 & Still Reba McEntire U2 Ft Mary J Blige & The Angels Sing Barry Manilow 1 & 1 Robert Miles & The Beat Goes On Whispers 1 000 Times A Day Patty Loveless & The Cradle Will Rock Van Halen 1 2 I Love You Clay Walker & The Crowd Goes Wild Mark Wills 1 2 Step Ciara Ft Missy Elliott & The Grass Wont Pay -

Administration of Donald J. Trump, 2019 Remarks At
Administration of Donald J. Trump, 2019 Remarks at the "Made in America" Product Showcase and an Exchange With Reporters July 15, 2019 [As the President approached the podium, "Hail to the Chief" was played.] The President. That sounds nice, doesn't it? [Laughter] Beautiful. Thank you very much. And thank you very much. Terrific talent. Please sit down. Please. I want welcome everyone to the White House. We are very excited to be hosting our third annual "Made in America" Showcase. It's all about "Made in America." We just started this, and this is my third already. And I just went around and saw these incredible companies that make everything from the THAAD missiles to beautiful boats. And I said, "How would that boat do against the THAAD missile?" And it wasn't a good answer. [Laughter] The boat is going to have a little problem, but that's okay. But I just want to say the engineering—inside, as you know, we have incredible things. I'm going in right now to look. I saw some of it yesterday. Incredible things. Made in the U.S.A. We're here today to celebrate and support the most incredible products in the world. And this is just a very representative sampling, because we're making more product here than we ever have. Joining us today are manufacturers from all 50 States. And they are terrific talents, terrific craftsmen, terrific businesspeople. We have hats from Wyoming, sandals from Florida, Tabasco from Louisiana, Airstream trailers—the Airstream is a great trailer; I've seen it for many years, and they're doing better than ever—from Ohio, and custom-built motorcycles from the great State of Indiana. -

(360) 575-7000 AGENDA REGULAR BOARD MEETING Date: Ma
Longview School District No. 122 2715 Lilac Street, Longview, WA 98632 - (360) 575-7000 AGENDA REGULAR BOARD MEETING Date: May 10, 2021 Time: 6:30 p.m. Place: Remote ZOOM Meeting To join the remote ZOOM meeting, please dial 1-253-215-8782 or click on this link https://longview122.zoom.us/j/92632503645 and enter the codes below when prompted: Meeting ID: 926 3250 3645 Passcode: 007018 5-10-1 Call Regular Meeting to Order 5-10-2 Flag Salute 5-10-3 Approval of Regular Meeting Agenda 5-10-4 Approval of Consent Agenda a. April 26, 2021 Regular Meeting Minutes b. Personnel Report c. WIAA Membership Renewal for 2021-22 (Resolution and Form) d. Warrants 5-10-5 Superintendent’s Report • Graduation Update 5-10-6 Requests to address the Board (three (3) minute limit per person please) 5-10-7 ELL Transitional Bilingual Report 5-10-8 2021-22 Budget Development Update 5-10-9 Policy 3205 Sexual Harassment of Students Prohibited (second reading) 5-10-10 Procedure 3205 Sexual Harassment of Student Prohibited (second reading) 5-10-11 Discussion - Academic and Student Well-Being Recovery Plan 5-10-12 Information Items A. Board Subcommittee Reports B. Legislative Updates C. Possible Future Board Agenda Items D. Other – Board Member Comments 5-10-13 Adjournment Board of Directors Don Wiitala, President Jennifer Leach, Vice President CJ Nickerson Barb Westrick Crystal Moldenhauer Longview School District No. 122 Regular Meeting of the Board of Directors Long Agenda May 10, 2021, 6:30 p.m. REMOTE ZOOM MEETING To join the remote ZOOM meeting, please dial 1-253-215-8782 or click on this link https://longview122.zoom.us/j/92632503645 and enter the codes below when prompted: Meeting ID: 926 3250 3645 Passcode: 007018 5-10-1 CALL REGULAR MEETING TO ORDER AND READING OF THE MISSION STATEMENT (1 MIN) The mission of the Longview School District is to ensure that every student learns the knowledge, skills, attitudes, and behaviors to become a responsible citizen in a rapidly changing world. -

Dan Blaze's Karaoke Song List
Dan Blaze's Karaoke Song List - By Artist 112 Peaches And Cream 411 Dumb 411 On My Knees 411 Teardrops 911 A Little Bit More 911 All I Want Is You 911 How Do You Want Me To Love You 911 More Than A Woman 911 Party People (Friday Night) 911 Private Number 911 The Journey 10 cc Donna 10 cc I'm Mandy 10 cc I'm Not In Love 10 cc The Things We Do For Love 10 cc Wall St Shuffle 10 cc Dreadlock Holiday 10000 Maniacs These Are The Days 1910 Fruitgum Co Simon Says 1999 Man United Squad Lift It High 2 Evisa Oh La La La 2 Pac California Love 2 Pac & Elton John Ghetto Gospel 2 Unlimited No Limits 2 Unlimited No Limits 20 Fingers Short Dick Man 21st Century Girls 21st Century Girls 3 Doors Down Kryptonite 3 Oh 3 feat Katy Perry Starstrukk 3 Oh 3 Feat Kesha My First Kiss 3 S L Take It Easy 30 Seconds To Mars The Kill 38 Special Hold On Loosely 3t Anything 3t With Michael Jackson Why 4 Non Blondes What's Up 4 Non Blondes What's Up 5 Seconds Of Summer Don't Stop 5 Seconds Of Summer Good Girls 5 Seconds Of Summer She Looks So Perfect 5 Star Rain Or Shine Updated 08.04.2015 www.blazediscos.com - www.facebook.com/djdanblaze Dan Blaze's Karaoke Song List - By Artist 50 Cent 21 Questions 50 Cent Candy Shop 50 Cent In Da Club 50 Cent Just A Lil Bit 50 Cent Feat Neyo Baby By Me 50 Cent Featt Justin Timberlake & Timbaland Ayo Technology 5ive & Queen We Will Rock You 5th Dimension Aquarius Let The Sunshine 5th Dimension Stoned Soul Picnic 5th Dimension Up Up and Away 5th Dimension Wedding Bell Blues 98 Degrees Because Of You 98 Degrees I Do 98 Degrees The Hardest -

Songs by Title
16,341 (11-2020) (Title-Artist) Songs by Title 16,341 (11-2020) (Title-Artist) Title Artist Title Artist (I Wanna Be) Your Adams, Bryan (Medley) Little Ole Cuddy, Shawn Underwear Wine Drinker Me & (Medley) 70's Estefan, Gloria Welcome Home & 'Moment' (Part 3) Walk Right Back (Medley) Abba 2017 De Toppers, The (Medley) Maggie May Stewart, Rod (Medley) Are You Jackson, Alan & Hot Legs & Da Ya Washed In The Blood Think I'm Sexy & I'll Fly Away (Medley) Pure Love De Toppers, The (Medley) Beatles Darin, Bobby (Medley) Queen (Part De Toppers, The (Live Remix) 2) (Medley) Bohemian Queen (Medley) Rhythm Is Estefan, Gloria & Rhapsody & Killer Gonna Get You & 1- Miami Sound Queen & The March 2-3 Machine Of The Black Queen (Medley) Rick Astley De Toppers, The (Live) (Medley) Secrets Mud (Medley) Burning Survivor That You Keep & Cat Heart & Eye Of The Crept In & Tiger Feet Tiger (Down 3 (Medley) Stand By Wynette, Tammy Semitones) Your Man & D-I-V-O- (Medley) Charley English, Michael R-C-E Pride (Medley) Stars Stars On 45 (Medley) Elton John De Toppers, The Sisters (Andrews (Medley) Full Monty (Duets) Williams, Sisters) Robbie & Tom Jones (Medley) Tainted Pussycat Dolls (Medley) Generation Dalida Love + Where Did 78 (French) Our Love Go (Medley) George De Toppers, The (Medley) Teddy Bear Richard, Cliff Michael, Wham (Live) & Too Much (Medley) Give Me Benson, George (Medley) Trini Lopez De Toppers, The The Night & Never (Live) Give Up On A Good (Medley) We Love De Toppers, The Thing The 90 S (Medley) Gold & Only Spandau Ballet (Medley) Y.M.C.A. -
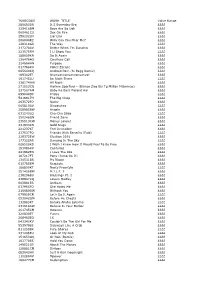
TUNECODE WORK TITLE Value Range 289693DR
TUNECODE WORK_TITLE Value Range 289693DR It S Everyday Bro ££££ 329418BM Boys Are So Ugh ££££ 060461CU Sex On Fire ££££ 258202LN Liar Liar ££££ 2680048Z Willy Can You Hear Me? ££££ 128318GR The Way ££££ 217278AV Better When I'm Dancing ££££ 223575FM I Ll Show You ££££ 188659KN Do It Again ££££ 136476HS Courtesy Call ££££ 224684HN Purpose ££££ 017788KU Police Escape ££££ 065640KQ Android Porn (Si Begg Remix) ££££ 189362ET Nyanyanyanyanyanyanya! ££££ 191745LU Be Right There ££££ 236174HW All Night ££££ 271523CQ Harlem Spartans - (Blanco Zico Bis Tg Millian Mizormac) ££££ 237567AM Baby Ko Bass Pasand Hai ££££ 099044DP Friday ££££ 5416917H The Big Chop ££££ 263572FQ Nasty ££££ 065810AV Dispatches ££££ 258985BW Angels ££££ 031243LQ Cha-Cha Slide ££££ 250248GN Friend Zone ££££ 235513CW Money Longer ££££ 231933KN Gold Slugs ££££ 221237KT Feel Invincible ££££ 237537FQ Friends With Benefits (Fwb) ££££ 228372EW Election 2016 ££££ 177322AR Dancing In The Sky ££££ 006520KS I Wish I Knew How It Would Feel To Be Free ££££ 153086KV Centuries ££££ 241982EN I Love The 90s ££££ 187217FT Pony (Jump On It) ££££ 134531BS My Nigga ££££ 015785EM Regulate ££££ 186800KT Nasty Freestyle ££££ 251426BW M.I.L.F. $ ££££ 238296BU Blessings Pt. 1 ££££ 238847KQ Lovers Medley ££££ 003981ER Anthem ££££ 037965FQ She Hates Me ££££ 216680GW Without You ££££ 079929CR Let's Do It Again ££££ 052042GM Before He Cheats ££££ 132883KT Baraka Allahu Lakuma ££££ 231618AW Believe In Your Barber ££££ 261745CM Ooouuu ££££ 220830ET Funny ££££ 268463EQ 16 ££££ 043343KV Couldn't Be The Girl -
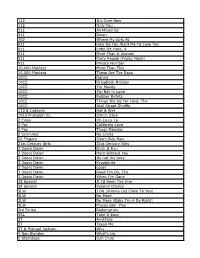
112 It's Over Now 112 Only You 311 All Mixed up 311 Down
112 It's Over Now 112 Only You 311 All Mixed Up 311 Down 702 Where My Girls At 911 How Do You Want Me To Love You 911 Little Bit More, A 911 More Than A Woman 911 Party People (Friday Night) 911 Private Number 10,000 Maniacs More Than This 10,000 Maniacs These Are The Days 10CC Donna 10CC Dreadlock Holiday 10CC I'm Mandy 10CC I'm Not In Love 10CC Rubber Bullets 10CC Things We Do For Love, The 10CC Wall Street Shuffle 112 & Ludacris Hot & Wet 1910 Fruitgum Co. Simon Says 2 Evisa Oh La La La 2 Pac California Love 2 Pac Thugz Mansion 2 Unlimited No Limits 20 Fingers Short Dick Man 21st Century Girls 21st Century Girls 3 Doors Down Duck & Run 3 Doors Down Here Without You 3 Doors Down Its not my time 3 Doors Down Kryptonite 3 Doors Down Loser 3 Doors Down Road I'm On, The 3 Doors Down When I'm Gone 38 Special If I'd Been The One 38 Special Second Chance 3LW I Do (Wanna Get Close To You) 3LW No More 3LW No More (Baby I'm A Do Right) 3LW Playas Gon' Play 3rd Strike Redemption 3SL Take It Easy 3T Anything 3T Tease Me 3T & Michael Jackson Why 4 Non Blondes What's Up 5 Stairsteps Ooh Child 50 Cent Disco Inferno 50 Cent If I Can't 50 Cent In Da Club 50 Cent In Da Club 50 Cent P.I.M.P. (Radio Version) 50 Cent Wanksta 50 Cent & Eminem Patiently Waiting 50 Cent & Nate Dogg 21 Questions 5th Dimension Aquarius_Let the sunshine inB 5th Dimension One less Bell to answer 5th Dimension Stoned Soul Picnic 5th Dimension Up Up & Away 5th Dimension Wedding Blue Bells 5th Dimension, The Last Night I Didn't Get To Sleep At All 69 Boys Tootsie Roll 8 Stops 7 Question -

“The Greatest Gift Is the Realization That Life Does Not Consist Either In
“The greatest gift is the realization that life does not consist either in wallowing in the past or peering anxiously into the future; and it is appalling to contemplate the great number of often painful steps by which ones arrives at a truth so old, so obvious, and so frequently expressed. It is good for one to appreciate that life is now. Whatever it offers, little or much, life is now –this day-this hour.” Charles Macomb Flandrau Ernest Hemingway drank here. Cuban revolutionaries Fidel Castro and Che Guevera drank here. A longhaired young hippie musician named Jimmy Buffett drank and performed here, too. From the 1930’s through today this rustic dive bar has seen more than its share of the famous and the infamous. It’s a little joint called Capt. Tony’s in Key West, Florida. Eighty-seven-year-old Anthony ‘Capt. Tony’ Tarracino has been the owner and proprietor of this boozy establishment since 1959. It seems Tony, as a young mobster, got himself into some serious trouble with ‘the family’ back in New Jersey and needed to lay low for a while. In those days, the mosquito invested ‘keys’ (or islands) on the southernmost end of Florida’s coastline was a fine place for wise guys on the lam to hide out. And this was well before the tee-shirt shops, restaurants, bars, art galleries, charming B&B’s and quaint hotels turned Key West into a serious year-round tourist destination. Sure, there were some ‘artsy’ types like Hemingway and Tennessee Williams living in Key West during the late 50’s when Tony bought the bar, but it was a seaside shanty town where muscular hard-working men in shrimp boats and cutters fished all day for a living. -

When We Were Sisters by Emilie Richards Excerpt CHAPTER ONE
When We Were Sisters by Emilie Richards Excerpt CHAPTER ONE Robin The stories of our lives can be told in so many ways, but no one account, no matter how carefully rendered, is completely true. Words are, at best, only an outline, something I discovered years ago whenever I was asked about my childhood. In the same way. I'm sure I'll tell the story of last night's accident differently every time I'm forced to recount it. I hope that won't be often. Right up until the minute I slid into the backseat of Gretchen Wainwright's Camry, I remember everything that happened yesterday. For better or worse I remember little that happened afterwards. The neurologist on call at the hospital promised that wisps of amnesia are not unusual, that after even a minor brain injury, patients often recount "islands of memory," when past events are viewed through fog. Sometimes the fog lifts, and blessedly sometimes it does not. Here's what I do recall. Meadow Branch, a housing development just outside Leesburg, Virginia, is more than my home. This little patch of earth is my refuge and my center. The friends I've made here are more important to me than I am to them, which is not to say they don't care. They do. But I treasure each of them in a way they'll never understand. To my knowledge I am the only woman in our neighborhood who grew up without a real home or family. And before Meadow Branch I never had a friend who didn't blow away on the winds of fortune. -

Songs by Artist
Songs by Artist Title Title (Hed) Planet Earth 2 Live Crew Bartender We Want Some Pussy Blackout 2 Pistols Other Side She Got It +44 You Know Me When Your Heart Stops Beating 20 Fingers 10 Years Short Dick Man Beautiful 21 Demands Through The Iris Give Me A Minute Wasteland 3 Doors Down 10,000 Maniacs Away From The Sun Because The Night Be Like That Candy Everybody Wants Behind Those Eyes More Than This Better Life, The These Are The Days Citizen Soldier Trouble Me Duck & Run 100 Proof Aged In Soul Every Time You Go Somebody's Been Sleeping Here By Me 10CC Here Without You I'm Not In Love It's Not My Time Things We Do For Love, The Kryptonite 112 Landing In London Come See Me Let Me Be Myself Cupid Let Me Go Dance With Me Live For Today Hot & Wet Loser It's Over Now Road I'm On, The Na Na Na So I Need You Peaches & Cream Train Right Here For You When I'm Gone U Already Know When You're Young 12 Gauge 3 Of Hearts Dunkie Butt Arizona Rain 12 Stones Love Is Enough Far Away 30 Seconds To Mars Way I Fell, The Closer To The Edge We Are One Kill, The 1910 Fruitgum Co. Kings And Queens 1, 2, 3 Red Light This Is War Simon Says Up In The Air (Explicit) 2 Chainz Yesterday Birthday Song (Explicit) 311 I'm Different (Explicit) All Mixed Up Spend It Amber 2 Live Crew Beyond The Grey Sky Doo Wah Diddy Creatures (For A While) Me So Horny Don't Tread On Me Song List Generator® Printed 5/12/2021 Page 1 of 334 Licensed to Chris Avis Songs by Artist Title Title 311 4Him First Straw Sacred Hideaway Hey You Where There Is Faith I'll Be Here Awhile Who You Are Love Song 5 Stairsteps, The You Wouldn't Believe O-O-H Child 38 Special 50 Cent Back Where You Belong 21 Questions Caught Up In You Baby By Me Hold On Loosely Best Friend If I'd Been The One Candy Shop Rockin' Into The Night Disco Inferno Second Chance Hustler's Ambition Teacher, Teacher If I Can't Wild-Eyed Southern Boys In Da Club 3LW Just A Lil' Bit I Do (Wanna Get Close To You) Outlaw No More (Baby I'ma Do Right) Outta Control Playas Gon' Play Outta Control (Remix Version) 3OH!3 P.I.M.P. -

The Weeknd Announces First Ever Tour in Asia
THE WEEKND ANNOUNCES FIRST EVER TOUR IN ASIA ‘The Weeknd is an undoubted global superstar’– NME ‘An orgasmic crowd pleaser’ – GQ LOS ANGELES, CA (August 13, 2018) – Grammy Award®-winning and multi-platinum selling music artist The Weeknd unveiled details behind his first-ever tour in Asia. The Weeknd Live In Asia will kick off on Friday, 30 November in Hong Kong, and visit 6 additional cities across Asia including Bangkok, Singapore, Manila, Taipei, Seoul, and Tokyo. Promoted by Live Nation, the tour will support the genre-spanning artist’s highly-acclaimed projects – Beauty Behind the Madness, Starboy, and My Dear Melancholy – all of which have been littered with chart-topping hits. Starting off his career anonymously, The Weeknd first broke into the music scene with the 2011 mixtape House of Balloons followed by studio album Kiss Land in 2013 and the widely recognized Beauty Behind the Madness that earned him two Grammy Awards in 2015, an RIAA triple-platinum certification for cumulative sales in excess of 3 million, 22 RIAA certifications from tracks alone with “The Hills” [9x-platinum], “Can’t Feel My Face” [7x-platinum], “Often” [3x-platinum], “In The Night” [2x-platinum], and “Acquainted” [platinum]. “Earned It (Fifty Shades of Grey)” even garnered The Weeknd his first ever Academy Award® nomination in the category of “Best Original Song.” The Weeknd’s fourth full-length album “Starboy” is set for release November 25, 2016. The title track featuring Daft Punk broke the record for “Most Release Weekend Streams Ever” upon its release. In less than a week, the single amassed over 17 million streams globally and 6.5 million streams in the United States, becoming #1 Most Added at Top 40, Rhythm, Urban, and Hot AC. -

Music Is GREAT Edition 4, October 2015
A guide Brought to you by for international media Edition 4 – October 2015 Festival No 6 Portmeirion, Wales visitbritain.com/media Contents Quick facts about Music in Britain......................................................................................................... 2 Music is Great – why? ............................................................................................................................... 3 10 must-do music activities in Britain ................................................................................................... 4 Music venues in Britain – a guide .......................................................................................................... 5 Music venues by music genre ............................................................................................................... 13 British music through the decades ...................................................................................................... 16 You saw them here first ......................................................................................................................... 18 Lyrical Britain: let the music be your guide ..................................................................................... 20 Step into British album covers ............................................................................................................. 24 Immersive music experiences .............................................................................................................