DOCSLIB.ORG

Physics-Subatomic-Particles.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Physics-Subatomic-Particles.Pdf ~~N ."$ II itOLit At .A Qo THE PHYSICS OF SUBATOMIC PARTICLES . S t e p h e n W o l f r a mm I 1 t • ~WNAI f' CONTENT S. Chapter One The Early History of Particle Physic s Chapter Two Some Basic Principle s Chapter Three The m clusion Principle, Antimatter, and Yukawas Hypothesi s Chapter Four he Proliferation of Particles Chapter Five eactions Chapter Six Symmetry and Structure Chapter Seven Interaction s Chapter Eight The Detection of Particle s Chapter Nine The Acceleration of Particle s Bibliography Appendix A Properties of Particles and Fields Appendix B Abbreviation s Appendix C Unit s Appendix 0 The Greek Alphabe t Appendix E Particle Accelerators Appendix F Physical constants CHAPTER ONE : THE EARLY HISTORY OF PARTICLE PHYSICS . In the fifth century B .C . a Greek philosopher named Democritus predicted th e existence of atoms (indivisible things), of which, in different patterns and motions , he believed everything to be made . At about this time, with the teaching of Democritu s and Leucippus, an idea of mass conservation and the discontinuity of matter began t o take shape . During its existence, the Pythagorean School of philosophers put forward fo r the first time the theory that light was composed of discrete corpuscles emitted from luminous bodies . In the first century B .C ., the Roman poet Lucretius colourfull y expressed these and other ideas on the nature of the universe, in his great didacti c poem De Rerum Natur0. ' (On the Nature of Things) . But however much these ancien t theories of discontinuity may seem to be ahead of their time, it should be remembere d that at the same time, almost equal support was gained for a continuous theory of th e universe, which was upheld. with much zeal by Heraclitus and the Eleatic philosophers . But neither of the two theories had any experimental proof to back them up, and s o were both of purely philosophical interest . Between the time of these Classical philosophers and the discovery of the firs t experimental basis for either theory, the controversy continued, and in the intervenin g twenty—three centuries many great scientists and philosophers, notably Newton and Descartes, considered the problem . On the whole, the continuous theory of matter an d light, as a wave, was favoured and it was not until the work of Brown in 1827 that the balance began to tip . He noticed some seemingly unprovoked movements of ligh t particles in aqueous solutions, and proposed a discontinuous molecular theory to accoun t for this . Then, after the work of Delsaux, Wiener, and Carbonelle in the period 186 3 to 1895, the Molecular Theory of solids, l iq uids, and gases, became firmly established . This had, among other things, the regular structures of crystals and the similaritie s between these and the proposed structures of molecules of particular substances (notably ' left— and right—handed Tartaric acid, as investigated by Pasteur), to back it up . It was after the discovery of electricity that the history of•Particle Physics a s a true science began . This discovery made Crookes investigate the nature of an electri c charge when passed thraagh a near—vacuum inside a sealed glass tube . In 1878 he made a spark from an induction coil traverse a sealed glass tube in which there was rarifie d inert gas, and observed a number of interesting phenomena . The first of these was th e rotation of the vanes of a radiometer, a tiny mica windmill, when it was place d inside one of these tubes, and this he attributed to molecular pressure . He als o performed the now classic experiment of putting flat aluminium discs of varying shap e between the two electrodes, and then observing the sharp shadows produced on a scree n at the end of the tube (by the positive electrode) . He found that light was evolved when the rays were stopped by the glass walls of the tube, and that this light wa s caused by an actual luminescence of the surface of the glass rather than by th e excitation of gas molecules . If this was happening then the emitted light would bea r some of the spectral characteristics of the gas filling the tube . Crookes also foun d that some substances, for example mica and quartz, did not emit light however close the y were brought to the negative electrode, and that, generally speaking, the mor e fluorescent the substance was, the greater the luminosity produced . Crookes also found that cathode rays discharged electroscopes (see chapter 8), and, which was even mor e important, they were deflected by a magnetic field . Crookes believed that he had found something even smaller than the atoms which had been believed to be the ultimat e stage in the division of matter and to behave like billiard-balls . In 1895 Jean Perrin, amid the controversy between scientists concerning the nature of cathode rays (some scientists, especially German ones, believed them to be due to some hitherto unknown process in the ether, while others believed them to consist of material particles with negative electric charges) repeated Crookes experiment o f deflecting cathode rays by a magnetic field . He proved that they were negativel y charged, and even collected the negative charges, but failed to perform any worthwhil e experiment on single particles . Thus he had practically proved that cathode rays wer e streams of electrified particles in rapid motion, and in 1897, J .J .Thomson, in hi s much celebrated experiment, discovered the constant ratio of the electric charges o f these particles to their masses . Although Hertz had previously tried to deflec t cathode rays by making them pass between two parallel metal plates across which a n electrostatic field had been produced by connection to a battery of electric cells , but had been unsuccessful, Thomson succeeded by using a more complete vacuum . Th e details of the experiment he performed were as follows : cathode rays were produced b y a hot wire at the cathode, and passed through two metal plugs which served as the anodes, and then between two aluminium plates 1 .5 ens . apart, both rectangular with dimension 5 ems . by 2 ems ., and finally hit a fluorescent screen on which they produce d a dot . When there was a high vacuum in the tube, the rays were seen to be repelled b y the negative plate and attracted by the positive one . The angle of deflection wa s shown to be directly proportional to the potential difference between the two plates . Thus the ratio of the electric charge of these particles to their mass was found t o be of the order of ten to the power of seven (ten million), a value much higher tha n any previously observed for other particles . The highest value then observed was tha t for the hydrogen ion, which was ten to the power of four . The charge to mass ratio for an electron is now accepted as being 1 .758796(6) x 10° C kg . But although Thomson s measurement of this fundamental constant was a great step forward, it gave no idea o f the independant values of either the electric charge or the mass of the cathode ra y particle . The cathode ray particle was christened the electron by Thomson . However, in 1924, R.A .Hillikan did manage to measure the charge of the electron o n its own . In his experiment oil droplets which had passed through a commercial atomiser using specially purified air, were allowed to fall in a large chamber, at the bottom of which there was a circular brass plate 22 ems, in diameter, with a pin-hole at it s centre . This plate formed one pole of an air condenser, whose other pole was a bras s plate held 16 mms . beneath the first by three ebonite rods . A three-way switch made it possible to control the charges of the plates, so that they had a potential differenc e of ten thousand volts when the switch was in two of its positions (in one, a given plate was positively charged, in the other it was negatively charged), and a potential difference of zero when it was in its third position . Any oil droplets which passed through the pin-hole were strongly illuminated, so that they could be observed, an d were then allowed to drop until they were very close to the negative plate (the lowe r one), when the switch was closed, and a potential difference was created between th e plates . This forced the oil droplet, which had been electrified by friction in th e atomiser, to rise, but when it was near the upper plate, the switch was opened agai n and the droplet fell under the influence of gravity . This cycle was repeated many times, and the time of fall, and therefore speed, of the droplet during each cycle was carefully measured . Millikan assumed, as had his predecessors, that the velocity of a droplet is proportional purely to the force acting upon it, and has nothing to do with the charg e on the droplet itself . As an electrified droplet passed through the air between th e two plates of the condenser, it sometimes picked up one or two ions, which increase d its electric charge, and thus the velocity with which it was attracted to the plate of opposite charge . It was found that the addition of an ion to the droplet caused a constant decrease in the time taken between the two plates on the upward journey , except in a few cases, when two ions had attached themselves onto the droplet, wher e the time was decreased by precisely twice the usual ampunt .
Load more

Recommended publications
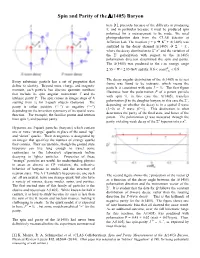
  • Spin and Parity of the Λ(1405) Baryon
    Spin and Parity of the (1405) Baryon here [1], precisely because of the difficulty in producing it, and in particular because it must be produced spin polarized for a measurement to be made. We used photoproduction data from the CLAS detector at Jefferson Lab. The reaction + p K+ + (1405) was analyzed in the decay channel (1405) + + , where the decay distribution to + and the variation of the + polarization with respect to the (1405) polarization direction determined the spin and parity. The (1405) was produced in the c.m. energy range K 2.55 < W < 2.85 GeV and for 0.6 coscm.. 0.9 . The decay angular distribution of the (1405) in its rest Every subatomic particle has a set of properties that frame was found to be isotropic, which means the define its identity. Beyond mass, charge, and magnetic particle is consistent with spin J = ½. The first figure moment, each particle has discrete quantum numbers illustrates how the polarization P of a parent particle that include its spin angular momentum J and its with spin ½, in this case the (1405), transfers intrinsic parity P. The spin comes in integer steps of ԰ + starting from ½ for 3-quark objects (baryons). The polarization Q to the daughter baryon, in this case the , depending on whether the decay is in a spatial S wave parity is either positive (“+”) or negative (“”) (L=0) or P wave (L=1). This distinction is what depending on the inversion symmetry of its spatial wave determines the parity of the final state, and hence of the function. For example, the familiar proton and neutron parent.
    [Show full text]
  • Electron-Nucleon Scattering at LDMX for DUNE
    Snowmass Letter of Intent: Snowmass Topical Groups: NF6, RF6, TF11 Electron-Nucleon Scattering at LDMX for DUNE Torsten Akesson1, Artur Ankowski2, Nikita Blinov3, Lene Kristian Bryngemark4, Pierfrancesco Butti2, Caterina Doglioni1, Craig Dukes5, Valentina Dutta6, Bertrand Echenard7, Thomas Eichlersmith8, Ralf Ehrlich5, Andrew Furmanski∗8, Niramay Gogate9, Mathew Graham2, Craig Group5, Alexander Friedland2, David Hitlin7, Vinay Hegde9, Christian Herwig3, Joseph Incandela6, Wesley Ketchumy3, Gordan Krnjaic3, Amina Li6, Shirley Liz2,3, Dexu Lin7, Jeremiah Mans8, Cristina Mantilla Suarez3, Phillip Masterson6, Martin Meier8, Sophie Middleton7, Omar Moreno2, Geoffrey Mullier1, Tim Nelson2, James Oyang7, Gianluca Petrillo2, Ruth Pottgen1, Stefan Prestel1, Luis Sarmiento1, Philip Schuster2, Hirohisa Tanaka2, Lauren Tompkins4, Natalia Toro2, Nhan Tran§3, and Andrew Whitbeck9 1Lund University 2Stanford Linear Accelerator Laboratory 3Fermi National Accelerator Laboratory 4Stanford University 5University of Virginia 6University of California Santa Barbara 7California Institute of Technology 8University of Minnesota 9Texas Tech University ABSTRACT We point out that the LDMX (Light Dark Matter eXperiment) detector design, conceived to search for sub-GeV dark matter, will also have very advantageous characteristics to pursue electron-nucleus scattering measurements of direct relevance to the neutrino program at DUNE and elsewhere. These characteristics include a 4-GeV electron beam, a precision tracker, electromagnetic and hadronic calorimeters with near 2p azimuthal acceptance from the forward beam axis out to 40◦ angle, and low reconstruction energy threshold. LDMX thus could provide (semi)exclusive cross section measurements, with∼ detailed information about final-state electrons, pions, protons, and neutrons. We compare the predictions of two widely used neutrino generators (GENIE, GiBUU) in the LDMX region of acceptance to illustrate the large modeling discrepancies in electron-nucleus interactions at DUNE-like kinematics.
    [Show full text]
  • The Subatomic Particle Mass Spectrum
    The Subatomic Particle Mass Spectrum Robert L. Oldershaw 12 Emily Lane Amherst, MA 01002 USA [email protected] Key Words: Subatomic Particles; Particle Mass Spectrum; General Relativity; Kerr Metric; Discrete Self-Similarity; Discrete Scale Relativity 1 Abstract: Representative members of the subatomic particle mass spectrum in the 100 MeV to 7,000 MeV range are retrodicted to a first approximation using the Kerr solution of General Relativity. The particle masses appear to form a restricted set of quantized values of a Kerr- based angular momentum-mass relation: M = n1/2 M, where values of n are a set of discrete integers and M is a revised Planck mass. A fractal paradigm manifesting global discrete self- similarity is critical to a proper determination of M, which differs from the conventional Planck mass by a factor of roughly 1019. This exceedingly simple and generic mass equation retrodicts the masses of a representative set of 27 well-known particles with an average relative error of 1.6%. A more rigorous mass formula, which includes the total spin angular momentum rule of Quantum Mechanics, the canonical spin values of the particles, and the dimensionless rotational parameter of the Kerr angular momentum-mass relation, is able to retrodict the masses of the 8 dominant baryons in the 900 MeV to 1700 MeV range at the < 99.7% > level. 2 “There remains one especially unsatisfactory feature [of the Standard Model of particle physics]: the observed masses of the particles, m. There is no theory that adequately explains these numbers. We use the numbers in all our theories, but we do not understand them – what they are, or where they come from.
    [Show full text]
  • FUNDAMENTAL PARTICLES Year 14 Physics Erin Hannigan
    FUNDAMENTAL PARTICLES Year 14 Physics Erin Hannigan 1 Key Word List ■ Natural Philosophy – the science of matter and energy and their interactions. ■ Hadron – any elementary particle that interacts strongly with other particles. ■ Lepton – an elementary particle that participates in weak interactions. ■ Subatomic Particle – a body having finite mass and internal structure but negligible dimensions. ■ Quark – any of a number f subatomic particles carrying a fractional electric charge, postulated as building blocks of the hadrons. Quarks have not been directly observed but theoretical predictions based on their existence have been confirmed experimentally. ■ Atom – the smallest component of an element having the chemical properties of the element. 2 Fundamental Particles ■ Fundamental particles (also called elementary particles) are the smallest building blocks of the universe. The key characteristic of fundamental particles is that they have no internal structure. ■ There are two type of fundamental particles: – Particles that make up all matter, called fermions – Particles that carry force, called bosons ■ The four fundamental forces include: – Gravity – The weak force – Electromagnetism – The strong force 3 The Four Fundamental Forces ■ The four fundamental forces of nature govern everything that happens in the universe. ■ Gravity – The attraction between two objects that have mass or energy ■ The weak force – Responsible for particle decay – Physicists describe this interaction through the exchange of force-carrying particles called
    [Show full text]
  • Introduction to Subatomic- Particle Spectrometers∗
    IIT-CAPP-15/2 Introduction to Subatomic- Particle Spectrometers∗ Daniel M. Kaplan Illinois Institute of Technology Chicago, IL 60616 Charles E. Lane Drexel University Philadelphia, PA 19104 Kenneth S. Nelsony University of Virginia Charlottesville, VA 22901 Abstract An introductory review, suitable for the beginning student of high-energy physics or professionals from other fields who may desire familiarity with subatomic-particle detection techniques. Subatomic-particle fundamentals and the basics of particle in- teractions with matter are summarized, after which we review particle detectors. We conclude with three examples that illustrate the variety of subatomic-particle spectrom- eters and exemplify the combined use of several detection techniques to characterize interaction events more-or-less completely. arXiv:physics/9805026v3 [physics.ins-det] 17 Jul 2015 ∗To appear in the Wiley Encyclopedia of Electrical and Electronics Engineering. yNow at Johns Hopkins University Applied Physics Laboratory, Laurel, MD 20723. 1 Contents 1 Introduction 5 2 Overview of Subatomic Particles 5 2.1 Leptons, Hadrons, Gauge and Higgs Bosons . 5 2.2 Neutrinos . 6 2.3 Quarks . 8 3 Overview of Particle Detection 9 3.1 Position Measurement: Hodoscopes and Telescopes . 9 3.2 Momentum and Energy Measurement . 9 3.2.1 Magnetic Spectrometry . 9 3.2.2 Calorimeters . 10 3.3 Particle Identification . 10 3.3.1 Calorimetric Electron (and Photon) Identification . 10 3.3.2 Muon Identification . 11 3.3.3 Time of Flight and Ionization . 11 3.3.4 Cherenkov Detectors . 11 3.3.5 Transition-Radiation Detectors . 12 3.4 Neutrino Detection . 12 3.4.1 Reactor Neutrinos . 12 3.4.2 Detection of High Energy Neutrinos .
    [Show full text]
  • From Quark and Nucleon Correlations to Discrete Symmetry and Clustering
    From quark and nucleon correlations to discrete symmetry and clustering in nuclei G. Musulmanbekov JINR, Dubna, RU-141980, Russia E-mail: [email protected] Abstract Starting with a quark model of nucleon structure in which the valence quarks are strongly correlated within a nucleon, the light nu- clei are constructed by assuming similar correlations of the quarks of neighboring nucleons. Applying the model to larger collections of nucleons reveals the emergence of the face-centered cubic (FCC) sym- metry at the nuclear level. Nuclei with closed shells possess octahedral symmetry. Binding of nucleons are provided by quark loops formed by three and four nucleon correlations. Quark loops are responsible for formation of exotic (borromean) nuclei, as well. The model unifies independent particle (shell) model, liquid-drop and cluster models. 1 Introduction arXiv:1708.04437v2 [nucl-th] 19 Sep 2017 Historically there are three well known conventional nuclear models based on different assumption about the phase state of the nucleus: the liquid-drop, shell (independent particle), and cluster models. The liquid-drop model re- quires a dense liquid nuclear interior (short mean-free-path, local nucleon interactions and space-occupying nucleons) in order to predict nuclear bind- ing energies, radii, collective oscillations, etc. In contrast, in the shell model each point nucleon moves in mean-field potential created by other nucleons; the model predicts the existence of nucleon orbitals and shell-like orbital- filling. The cluster models require the assumption of strong local-clustering 1 of particularly the 4-nucleon alpha-particle within a liquid or gaseous nuclear interior in order to make predictions about the ground and excited states of cluster configurations.
    [Show full text]
  • The Ghost Particle 1 Ask Students If They Can Think of Some Things They Cannot Directly See but They Know Exist
    Original broadcast: February 21, 2006 BEFORE WATCHING The Ghost Particle 1 Ask students if they can think of some things they cannot directly see but they know exist. Have them provide examples and reasoning for PROGRAM OVERVIEW how they know these things exist. NOVA explores the 70–year struggle so (Some examples and evidence of their existence include: [bacteria and virus- far to understand the most elusive of all es—illnesses], [energy—heat from the elementary particles, the neutrino. sun], [magnetism—effect on a com- pass], and [gravity—objects falling The program: towards Earth].) How do scientists • relates how the neutrino first came to be theorized by physicist observe and measure things that cannot be seen with the naked eye? Wolfgang Pauli in 1930. (They use instruments such as • notes the challenge of studying a particle with no electric charge. microscopes and telescopes, and • describes the first experiment that confirmed the existence of the they look at how unseen things neutrino in 1956. affect other objects.) • recounts how scientists came to believe that neutrinos—which are 2 Review the structure of an atom, produced during radioactive decay—would also be involved in including protons, neutrons, and nuclear fusion, a process suspected as the fuel source for the sun. electrons. Ask students what they know about subatomic particles, • tells how theoretician John Bahcall and chemist Ray Davis began i.e., any of the various units of mat- studying neutrinos to better understand how stars shine—Bahcall ter below the size of an atom. To created the first mathematical model predicting the sun’s solar help students better understand the neutrino production and Davis designed an experiment to measure size of some subatomic particles, solar neutrinos.
    [Show full text]
  • First Results of the Cosmic Ray NUCLEON Experiment
    Prepared for submission to JCAP First results of the cosmic ray NUCLEON experiment E. Atkin,a V. Bulatov,b V. Dorokhov,b N. Gorbunov,c;d S. Filippov,b V. Grebenyuk,c;d D. Karmanov,e I. Kovalev,e I. Kudryashov,e A. Kurganov,e M. Merkin,e A. Panov,e;1 D. Podorozhny,e D. Polkov,b S. Porokhovoy,c V. Shumikhin,a L. Sveshnikova,e A. Tkachenko,c;f L. Tkachev,c;d A. Turundaevskiy,e O. Vasiliev ande A. Voronine aNational Research Nuclear University “MEPhI”, Kashirskoe highway, 31. Moscow, 115409, Russia bSDB Automatika, Mamin-Sibiryak str, 145, Ekaterinburg, 620075, Russia cJoint Institute for Nuclear Research, Dubna, Joliot-Curie, 6, Moscow region, 141980, Russia d arXiv:1702.02352v2 [astro-ph.HE] 2 Jul 2018 “DUBNA” University, Universitetskaya str., 19, Dubna, Moscow region, 141980, Russia eSkobeltsyn Institute of Nuclear Physics, Moscow State University, 1(2), Leninskie gory, GSP-1, Moscow, 119991, Russia f Bogolyubov Institute for Theoretical Physics, 14-b Metrolohichna str., Kiev, 03143, Ukraine 1Corresponding author. E-mail: [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], tfl[email protected], [email protected], [email protected], [email protected], [email protected], [email protected] Abstract.
    [Show full text]
  • 14. Structure of Nuclei Particle and Nuclear Physics
    14. Structure of Nuclei Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 14. Structure of Nuclei 1 In this section... Magic Numbers The Nuclear Shell Model Excited States Dr. Tina Potter 14. Structure of Nuclei 2 Magic Numbers Magic Numbers = 2; 8; 20; 28; 50; 82; 126... Nuclei with a magic number of Z and/or N are particularly stable, e.g. Binding energy per nucleon is large for magic numbers Doubly magic nuclei are especially stable. Dr. Tina Potter 14. Structure of Nuclei 3 Magic Numbers Other notable behaviour includes Greater abundance of isotopes and isotones for magic numbers e.g. Z = 20 has6 stable isotopes (average=2) Z = 50 has 10 stable isotopes (average=4) Odd A nuclei have small quadrupole moments when magic First excited states for magic nuclei higher than neighbours Large energy release in α, β decay when the daughter nucleus is magic Spontaneous neutron emitters have N = magic + 1 Nuclear radius shows only small change with Z, N at magic numbers. etc... etc... Dr. Tina Potter 14. Structure of Nuclei 4 Magic Numbers Analogy with atomic behaviour as electron shells fill. Atomic case - reminder Electrons move independently in central potential V (r) ∼ 1=r (Coulomb field of nucleus). Shells filled progressively according to Pauli exclusion principle. Chemical properties of an atom defined by valence (unpaired) electrons. Energy levels can be obtained (to first order) by solving Schr¨odinger equation for central potential. 1 E = n = principle quantum number n n2 Shell closure gives noble gas atoms. Are magic nuclei analogous to the noble gas atoms? Dr.
    [Show full text]
  • Electron- Vs Neutrino-Nucleus Scattering
    Electron- vs Neutrino-Nucleus Scattering Omar Benhar INFN and Department of Physics Universita` “La Sapienza” I-00185 Roma, Italy NUFACT11 University of Geneva, August 2nd, 2011 Neutrino-nucleus scattering . impact of the flux average . flux-averaged electron scattering x-section: a numerical experiment . contributions of reaction mechanisms other than quasi elastic single nucleon knock out to the MiniBooNE CCQE data sample Summary & Outlook Outline Electron scattering . standard data representation . theoretical description: the impulse approximation Omar Benhar (INFN, Roma) NUFACT11 Geneva 02/08/2011 2 / 24 Summary & Outlook Outline Electron scattering . standard data representation . theoretical description: the impulse approximation Neutrino-nucleus scattering . impact of the flux average . flux-averaged electron scattering x-section: a numerical experiment . contributions of reaction mechanisms other than quasi elastic single nucleon knock out to the MiniBooNE CCQE data sample Omar Benhar (INFN, Roma) NUFACT11 Geneva 02/08/2011 2 / 24 Outline Electron scattering . standard data representation . theoretical description: the impulse approximation Neutrino-nucleus scattering . impact of the flux average . flux-averaged electron scattering x-section: a numerical experiment . contributions of reaction mechanisms other than quasi elastic single nucleon knock out to the MiniBooNE CCQE data sample Summary & Outlook Omar Benhar (INFN, Roma) NUFACT11 Geneva 02/08/2011 2 / 24 The inclusive electron-nucleus x-section The x-section of the process e
    [Show full text]
  • Detection of a Strange Particle
    10 extraordinary papers Within days, Watson and Crick had built a identify the full set of codons was completed in forensics, and research into more-futuristic new model of DNA from metal parts. Wilkins by 1966, with Har Gobind Khorana contributing applications, such as DNA-based computing, immediately accepted that it was correct. It the sequences of bases in several codons from is well advanced. was agreed between the two groups that they his experiments with synthetic polynucleotides Paradoxically, Watson and Crick’s iconic would publish three papers simultaneously in (see go.nature.com/2hebk3k). structure has also made it possible to recog- Nature, with the King’s researchers comment- With Fred Sanger and colleagues’ publica- nize the shortcomings of the central dogma, ing on the fit of Watson and Crick’s structure tion16 of an efficient method for sequencing with the discovery of small RNAs that can reg- to the experimental data, and Franklin and DNA in 1977, the way was open for the com- ulate gene expression, and of environmental Gosling publishing Photograph 51 for the plete reading of the genetic information in factors that induce heritable epigenetic first time7,8. any species. The task was completed for the change. No doubt, the concept of the double The Cambridge pair acknowledged in their human genome by 2003, another milestone helix will continue to underpin discoveries in paper that they knew of “the general nature in the history of DNA. biology for decades to come. of the unpublished experimental results and Watson devoted most of the rest of his ideas” of the King’s workers, but it wasn’t until career to education and scientific administra- Georgina Ferry is a science writer based in The Double Helix, Watson’s explosive account tion as head of the Cold Spring Harbor Labo- Oxford, UK.
    [Show full text]
  • A Measurement of Neutral B Meson Mixing Using Dilepton Events with the BABAR Detector
    A measurement of neutral B meson mixing using dilepton events with the BABAR detector Naveen Jeevaka Wickramasinghe Gunawardane Imperial College, London A thesis submitted for the degree of Doctor of Philosophy of the University of London and the Diploma of Imperial College December, 2000 A measurement of neutral B meson mixing using dilepton events with the BABAR detector Naveen Gunawardane Blackett Laboratory Imperial College of Science, Technology and Medicine Prince Consort Road London SW7 2BW December, 2000 ABSTRACT This thesis reports on a measurement of the neutral B meson mixing parameter, ∆md, at the BABAR experiment and the work carried out on the electromagnetic calorimeter (EMC) data acquisition (DAQ) system and simulation software. The BABAR experiment, built at the Stanford Linear Accelerator Centre, uses the PEP-II asymmetric storage ring to make precise measurements in the B meson system. Due to the high beam crossing rates at PEP-II, the DAQ system employed by BABAR plays a very crucial role in the physics potential of the experiment. The inclusion of machine backgrounds noise is an important consideration within the simulation environment. The BABAR event mixing software written for this purpose have the functionality to mix both simulated and real detector backgrounds. Due to the high energy resolution expected from the EMC, a matched digital filter is used. The performance of the filter algorithms could be improved upon by means of a polynomial fit. Application of the fit resulted in a 4-40% improvement in the energy resolution and a 90% improvement in the timing resolution. A dilepton approach was used in the measurement of ∆md where the flavour of the B was tagged using the charge of the lepton.
    [Show full text]