DOCSLIB.ORG

The Rossby Wave As a Key Mechanism of Indian Ocean Climate Variability

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Rossby Wave As a Key Mechanism of Indian Ocean Climate Variability ARTICLE IN PRESS Deep-Sea Research I 51 (2004) 2123–2136 www.elsevier.com/locate/dsr The Rossby wave as a key mechanism of Indian Ocean climate variability Mark R. Jurya, Bohua Huangb aEnvironmental Science Department, Center for Environmental Studies, University of Zululand, KwaDlangezwa 3886, South Africa bCenter for Ocean Land Atmosphere Studies, Maryland, USA Received 18 November 2003; received in revised form 3 June 2004; accepted 3 June 2004 Available online 7 October 2004 Abstract We analyze the time-longitude structure of composite cases from model-assimilated ocean data in the period 1958–1998, following on from earlier work by Huang and Kinter (J. Geophys. Res. 107(C11) (2002) 3199) that studied east–west thermocline variability in the Indian Ocean. Our analysis focuses on the Rossby wave signal along the thermocline ridge in the tropical SW Indian Ocean (101S, 60–801E), where wind stress curl is important. Anomalous winds in the equatorial east Indian Ocean force successive Rossby waves westward at speeds of 0.1 m sÀ1730%. With a wavelength of 7000 km, the period of oscillation is in the range 1.9–5.2 years. The Indian Ocean Rossby wave is partially resonant with the global influence of the El Nino–Southern Oscillation, except during quasi-biennial rhythm. The presence of the Rossby wave offers potential predictability for east–west atmospheric circulation systems and climate that affect resources in countries surrounding the Indian Ocean. r 2004 Elsevier Ltd. All rights reserved. 1. Introduction Somalia and surface cooling off Madagascar. A zone of maximum convection occurs over the The west Indian Ocean (WIO) is a climatically eastern warm pool (51N–101S, 70–1001E) with important region, recording on average 10 tropical precipitation rates48 mm dayÀ1. Zonal winds in cyclones each year between December and March. the tropical Indian Ocean are weak within the These storms often bring devastating conse- equatorial wave-guide because of the prevailing quences to the Mascarene Islands, Madagascar meridional flow of the monsoon. The equatorial and Mozambique (Naeraa and Jury, 1998). The thermocline lies around 120 m depth and exhibits mean sea surface temperature (SST) in the WIO little east–west slope in contrast with the Pacific varies between 26 and 28 1C, and is cooler than the and Atlantic Oceans (Xie et al., 2002). The mean eastern Indian Ocean, due to upwelling off structure of the thermocline is a ridge–trough pair at 71Sand201S, respectively, with mean tempera- E-mail address: [email protected] (M.R. Jury). tures of 18 and 22 1C for the upper 234 m and 0967-0637/$ - see front matter r 2004 Elsevier Ltd. All rights reserved. doi:10.1016/j.dsr.2004.06.005 ARTICLE IN PRESS 2124 M.R. Jury, B. Huang / Deep-Sea Research I 51 (2004) 2123–2136 thermocline depths of 80 and 180 m, respectively. (Murtugudde et al., 2000; Behera and Yamagata, Due to the lack of a zonal gradient in the 2001; Xie et al., 2002). equatorial zone, it was thought that the Indian In the present study, we further investigate the Ocean may not have the appropriate features to mechanisms of ocean variability using model-assimi- develop its own El Nino–Southern Oscillation lated data, following Huang and Kinter (2002).Of (ENSO)-like interannual variability (Latif and particular interest is the nature of sub-tropical Barnett, 1995). Rossbywavesandtheirimpactontheclimate Yet, east–west gradients in the thermocline can system. Toward this end, we analyze in situ ocean develop at times (Hastenrath et al., 1993; Webster data assimilated by a numerical model (Schneider et al., 1999; Murtugudde et al., 2000; Ueda and et al., 1999). Key issues to be addressed include: the Matsumoto, 2000), with atmospheric circulation time-longitude structure of Rossby waves, the and convection varying in a manner consistent characteristics of phase propagation, preferred loca- with Bjerknes (1969) feedback. At the onset of a tions for wave amplification, and the extent of Pacific El Nino event as atmospheric convection coupling with the atmosphere. We conclude that shifts eastward from the warm pool, anomalous much of ocean variability comprising the east–west easterly winds develop near the equator in the east dipole in the Indian Ocean can be attributed to an Indian Ocean. These generate a gradual warming off-equatorial ocean Rossby wave that propagates to the west (Nigam and Shen, 1993; Klein et al., slowly from the east following a surge of wind at the 1999; Lau and Nath, 2000) that will be further onsetofmostElNinoevents.Thepaperisorganized explored here. into sections on data and methods, results sub- Although surface fluxes explain changes in SST divided into wave character and zonal phase over much of the tropical Indian Ocean, this is less propagation (hovmoller analysis), and discussion. so in the thermocline ridge (5–121S, 55–851E) according to the results of Klein et al. (1999), Lau and Nath (2000). Ocean model results 2. Data and methods (Murtugudde and Busalacchi, 1999; Murtugudde et al., 2000) and analysis of sea surface height Upper ocean heat content fields (mean tempera- measurements (Chambers et al., 1999) suggest that ture in the top 234 m) for the period 1958–1998 dynamic processes contribute to SST variability in have been derived from an ocean data assimilation the tropical Indian Ocean. Huang and Kinter system operated at COLA as outlined in Huang (2000, 2001, 2002) have used upper ocean heat and Kinter (2002), hereafter HK02. The data content from data-assimilated ocean analyses to assimilation uses a variational scheme (Derber and identify the westward propagating Rossby wave as Rosati, 1989) to combine temperature observa- a key feature of the near-continuous interannual tions in an ocean general circulation model oscillation of the upper tropical Indian Ocean (oGCM). The analysis uses all observations since the late 1950s. This result substantiated the available in a moving 10-day assimilation window. finding from the TOPEX/Poseidon altimeter The observations are inserted into the first guess measurements during the 1990s. Observational field of the oGCM and discrepancies are iteratively studies of warm and cool events (Reason et al., minimized. The oGCM is a version of the GFDL 2000; Jury et al., 2002) demonstrate that local heat modular ocean model (Huang and Schneider, and radiative fluxes, and vertical entrainment from 1995; Schneider et al., 1999; Huang et al., 2002). wind stress curl account for a significant portion of It is forced by monthly averaged surface wind SST variance during onset phase. However, the stress from NCEP reanalysis available at an surface heat fluxes do not fully explain the irregular grid with a variable resolution of around variations of SST there from fall to next spring. 21 near the equator. The solar flux is prescribed The lack of closure in the budget for local SST (Oberhuber, 1988), surface heat and long-wave changes in the WIO may be attributed to fluxes are parameterized (Philander et al., 1987; horizontal advection via incoming Rossby waves Rosatiand Miyakoda,1988). ARTICLE IN PRESS M.R. Jury, B. Huang / Deep-Sea Research I 51 (2004) 2123–2136 2125 Ocean temperature observations are assimilated more observations along key lines from Perth to from in situ SST measurements from the COADS the NW, from Madagascar to the NE, from archive (Slutz et al., 1985), temperature profile Mauritius to the north, and from Mombassa to (XBT, MBT, CTD, etc.) measurements (Conk- the east (Masumoto and Meyers, 1998), which are right et al., 1998) and, since 1981, with satellite- important for our present study. However, some blended weekly SST fields (Reynolds and Smith, of these, especially in the South Indian Ocean, 1994). The number of temperature profiles is were established with TOGA in 1985. generally 3000–9000 per year within the square Fig. 1a and b shows the spatial distributions of between 301Eand1201E, 301S and 301N during the temperature profiles per degree-square for the the 41 years (see Fig. 1 a and b). In 1967, 1968, and years 1958–1980 and 1981–1998. It is evident that 1979, it surpassed 15000 profiles. In situ SST measurements on major ship tracks were enhanced measurements exceeded 90,000 per year, reaching in the later period in the South Indian Ocean. Even a maximum of 270,000 per year. However, many after this enhancement, the distribution of the sub- of these observations, especially the sub-surface surface temperature observations was still sparse data, are concentrated along the coasts. There are and may be wider than the typical zonal decorr- elation scale in the equatorial ocean (Smith, 1995). Therefore, the assimilated product is inevitably Distribution of Temperature Profiles strongly affected by the ocean model and the Profile Number, 1958-1980 30N surface forcing fields. The model-derived results 25N are considered in this light and we therefore 20N employ analysis techniques that highlight repeti- 15N tious patterns (e.g., EOF, composite). 10N The anomalies of model-analyzed upper ocean 5N 5000 heat content are highly correlated with the EQ 5S 1000 independently derived sea surface height anoma- lies from the TOPEX/Poseidon satellite altimeter 10S 500 15S measurements (HK02) using monthly data. It 20S 300 suggests that the assimilated temperatures are 25S 250 useful for analyzing the interannual variability in 30S 30E 40E 50E 60E 70E 80E 90E 100E 110E this region. One may attribute this high consis- (a) 200 tency to newly established ship data in recent 150 years. However, our EOF analysis of the heat Profile Number, 1981-1998 100 content anomalies (HCa) in different periods 30N 25N 75 shows very similar patterns. We believe that this data set is superior to an oGCM simulation with 20N 50 15N observed surface forcing only, because of insertion 10N 30 of the oceanographic observations.
Load more

Recommended publications
  • How the Ocean Affects Weather & Climate
    Ocean in Motion 6: How does the Ocean Change Weather and Climate? A. Overview 1. The Ocean in Motion -- Weather and Climate In this program we will tie together ideas from previous lectures on ocean circulation. The students will also learn about the similarities and interactions between the atmosphere and the ocean. 2. Contents of Packet Your packet contains the following activities: I. A Sea of Words B. Program Preparation 1. Focus Points OThe oceans and the atmosphere are closely linked 1. the sun heats the atmosphere as well as the oceans 2. water evaporates from the ocean into the atmosphere a. forms clouds and precipitation b. movement of any fluid (gas or liquid) due to heating creates convective currents OWeather and climate are two different things. 1. Winds a. Uneven heating and cooling of the atmosphere creates wind b. Global ocean surface current patterns are similar to global surface wind patterns c. wind patterns are analogous to ocean currents 2. Four seasons OAtmospheric motion 1. weather and air moves from high to low pressure areas 2. the earth's rotation also influences air and weather patterns 3. Atmospheric winds move surface ocean currents. ©1998 Project Oceanography Spring Series Ocean in Motion 1 C. Showtime 1. Broadcast Topics This broadcast will link into discussions on ocean and atmospheric circulation, wind patterns, and how climate and weather are two different things. a. Brief Review We know the modern reason for studying ocean circulation is because it is a major part of our climate. We talked about how the sun provides heat energy to the world, and how the ocean currents circulate because the water temperatures and densities vary.
    [Show full text]
  • Chapter 7 100 Years of the Ocean General Circulation
    CHAPTER 7 WUNSCH AND FERRARI 7.1 Chapter 7 100 Years of the Ocean General Circulation CARL WUNSCH Massachusetts Institute of Technology, and Harvard University, Cambridge, Massachusetts RAFFAELE FERRARI Massachusetts Institute of Technology, Cambridge, Massachusetts ABSTRACT The central change in understanding of the ocean circulation during the past 100 years has been its emergence as an intensely time-dependent, effectively turbulent and wave-dominated, flow. Early technol- ogies for making the difficult observations were adequate only to depict large-scale, quasi-steady flows. With the electronic revolution of the past 501 years, the emergence of geophysical fluid dynamics, the strongly inhomogeneous time-dependent nature of oceanic circulation physics finally emerged. Mesoscale (balanced), submesoscale oceanic eddies at 100-km horizontal scales and shorter, and internal waves are now known to be central to much of the behavior of the system. Ocean circulation is now recognized to involve both eddies and larger-scale flows with dominant elements and their interactions varying among the classical gyres, the boundary current regions, the Southern Ocean, and the tropics. 1. Introduction physical regimes, understanding of the ocean until relatively recently greatly lagged that of the atmo- In the past 100 years, understanding of the general sphere. As in almost all of fluid dynamics, progress circulation of the ocean has shifted from treating it as an in understanding has required an intimate partnership essentially laminar, steady-state, slow, almost geological, between theoretical description and observational or flow, to that of a perpetually changing fluid, best charac- laboratory tests. The basic feature of the fluid dynamics terized as intensely turbulent with kinetic energy domi- of the ocean, as opposed to that of the atmosphere, has nated by time-varying flows.
    [Show full text]
  • Climate and Atmospheric Circulation of Mars
    Climate and QuickTime™ and a YUV420 codec decompressor are needed to see this picture. Atmospheric Circulation of Mars: Introduction and Context Peter L Read Atmospheric, Oceanic & Planetary Physics, University of Oxford Motivating questions • Overview and phenomenology – Planetary parameters and ‘geography’ of Mars – Zonal mean circulations as a function of season – CO2 condensation cycle • Form and style of Martian atmospheric circulation? • Key processes affecting Martian climate? • The Martian climate and circulation in context…..comparative planetary circulation regimes? Books? • D. G. Andrews - Intro….. • J. T. Houghton - The Physics of Atmospheres (CUP) ALSO • I. N. James - Introduction to Circulating Atmospheres (CUP) • P. L. Read & S. R. Lewis - The Martian Climate Revisited (Springer-Praxis) Ground-based observations Percival Lowell Lowell Observatory (Arizona) [Image source: Wikimedia Commons] Mars from Hubble Space Telescope Mars Pathfinder (1997) Mars Exploration Rovers (2004) Orbiting spacecraft: Mars Reconnaissance Orbiter (NASA) Image credits: NASA/JPL/Caltech Mars Express orbiter (ESA) • Stereo imaging • Infrared sounding/mapping • UV/visible/radio occultation • Subsurface radar • Magnetic field and particle environment MGS/TES Atmospheric mapping From: Smith et al. (2000) J. Geophys. Res., 106, 23929 DATA ASSIMILATION Spacecraft Retrieved atmospheric parameters ( p,T,dust...) - incomplete coverage - noisy data..... Assimilation algorithm Global 3D analysis - sequential estimation - global coverage - 4Dvar .....? - continuous in time - all variables...... General Circulation Model - continuous 3D simulation - complete self-consistent Physics - all variables........ - time-dependent circulation LMD-Oxford/OU-IAA European Mars Climate model • Global numerical model of Martian atmospheric circulation (cf Met Office, NCEP, ECMWF…) • High resolution dynamics – Typically T31 (3.75o x 3.75o) – Most recently up to T170 (512 x 256) – 32 vertical levels stretched to ~120 km alt.
    [Show full text]
  • El Niño and La Niña
    About the Images What are El Niño and La Niña? The images show El Niño, neutral, and La Niña sea surface The naturally occurring El Niño and La Niña phenomenon rep- heights (SSHs) relative to a reference state established in resents a “dance” between the atmosphere and ocean in the 1992. In the equatorial region of the Pacific Ocean, the SSH equatorial Pacific Ocean. Sometimes the atmosphere leads the during El Niño was higher by more than 18 cm over a large ocean and causes ocean conditions, and sometimes the ocean longitudinal region. The warmer water associated with El Niño leads the atmosphere and produces atmospheric motions that— displaces colder water in the upper layer of the ocean causing when strong enough—influence global atmospheric circulation. an increase in SSH because of thermal expansion. During La Sea surface temperature (SST) is the critical variable connecting Niña the temperature of the upper ocean is lower than normal, the atmosphere and ocean. Since SSH measurements yield criti- causing SSH to decrease because of thermal contraction. The cal information about the depth of the subsurface temperatures, neutral condition occurs when the upper-ocean temperature e.g., the thermocline, they provide key information on the onset, is “normal.” Red and white shades indicate high SSHs relative maintenance, and dissipation of El Niño and La Niña events. to the reference state, while blue and purple shades indicate SSHs lower than the reference state. Neutral conditions appear The 2015 El Niño Event green. The El Niño and neutral images are derived using data After five consecutive months with SSTs 0.5 °C above the acquired by the Ocean Surface Topography Mission (OSTM)/Jason-2 long-term mean, the National Oceanic and Atmospheric Admin- satellite.
    [Show full text]
  • Atmospheric General Circulation
    LectureLecture 5:5: AtmosphericAtmospheric GeneralGeneral CirculationCirculation JS JP HadleyHadley CellCell FerrelFerrel CellCell PolarPolar CellCell (driven by eddies) LHL H Basic Structures and Dynamics General Circulation in the Troposphere General Circulation in the Stratosphere Wind-Driven Ocean Circulation ESS55 Prof. Jin-Yi Yu SingleSingle--CellCell Model:Model: ExplainsExplains WhyWhy ThereThere areare TropicalTropical EasterliesEasterlies Without Earth Rotation With Earth Rotation Coriolis Force (Figures from Understanding Weather & Climate and The Earth System) ESS55 Prof. Jin-Yi Yu BreakdownBreakdown ofof thethe SingleSingle CellCell ÎÎ ThreeThree--CellCell ModelModel Absolute angular momentum at Equator = Absolute angular momentum at 60°N The observed zonal velocity at the equatoru is ueq = -5 m/sec. Therefore, the total velocity at the equator is U=rotational velocity (U0 + uEq) The zonal wind velocity at 60°N (u60N) can be determined by the following: (U0 + uEq) * a * Cos(0°) = (U60N + u60N) * a * Cos(60°) (Ω*a*Cos0° - 5) * a * Cos0° = (Ω*a*Cos60° + u60N) * a * Cos(60°) u60N = 687 m/sec !!!! This high wind speed is not observed! ESS55 Prof. Jin-Yi Yu PropertiesProperties ofof thethe ThreeThree CellsCells thermally indirect circulation thermally direct circulation JS JP HadleyHadley CellCell FerrelFerrel CellCell PolarPolar CellCell (driven by eddies) LHL H Equator 30° 60° Pole (warmer) (warm) (cold) (colder) ESS55 Prof. Jin-Yi Yu AtmosphericAtmospheric Circulation:Circulation: ZonalZonal--meanmean ViewsViews Single-Cell Model Three-Cell Model (Figures from Understanding Weather & Climate and The Earth System) ESS55 Prof. Jin-Yi Yu TheThe ThreeThree CellsCells ITCZ Subtropical midlatitude High Weather system (Figures from Understanding Weather & Climate and The Earth System) ESS55 Prof. Jin-Yi Yu ThermallyThermally Direct/IndirectDirect/Indirect CellsCells Thermally Direct Cells (Hadley and Polar Cells) Both cells have their rising branches over warm temperature zones and sinking braches over the cold temperature zone.
    [Show full text]
  • The Earth's Rotation and Atmospheric Circulation, from 1963 to 1973 Kurt
    Geophys. J. R. astr. Soc. (1981) 64,67-89 The Earth’s rotation and atmospheric circulation, from 1963 to 1973 Kurt Lambeck and Peter Hopgood Research School of Earth Sciences, Australian National University, Canberra 2600, Australia Received 1980 June 13; in original form 1980 March 17 ‘If everybody minded their own business, the world would go round a deal faster than it does.’ Alice’s Adventures in Wonderland Lewis Carroll Summary. The zonal angular momentum of the atmospheric circulation has been evaluated month-by-month and compared with astronomical observa- tions of the length-of-day for the 10 years from 1963 May to 1973 April. The reason for undertaking this study is to enable the astronomical observa- tions to be ‘corrected’ for the zonal wind effect and to investigate the residual excitation function for solid-Earth contributions. The principal conclusions reached are the following: (i) The annual change in length-of-day is almost entirely due to the seasonal changes in the zonal circulation with tidal, oceanographic and hydrologic phenomena contributing together at most 10 per cent of the total excitation. (ii) The semi-annual term is pre- dominantly due to the zonal wind and the body tide, with oceanic and hydrologic terms contributing about 10 per cent. (iii) The atmospheric circulation plays a dominant role in length-of-day changes in the period range from 1 to about 4 yr. This is partly associated with the quasi-biennial oscilla- tion and its harmonics. Both the period and amplitude of these fluctuations are very variable. (iv) At longer periods the atmosphere may still contribute to the total excitation but other excitation functions begin to rise above the spectrum of the meteorological excitation.
    [Show full text]
  • Atmospheric Circulation and Weather Systems
    CHAPTER ATMOSPHERIC CIRCULATION AND WEATHER SYSTEMS arlier Chapter 9 described the uneven pressure is measured with the help of a distribution of temperature over the mercury barometer or the aneroid barometer. Esurface of the earth. Air expands when Consult your book, Practical Work in heated and gets compressed when cooled. This Geography — Part I (NCERT, 2006) and learn results in variations in the atmospheric about these instruments. The pressure pressure. The result is that it causes the decreases with height. At any elevation it varies movement of air from high pressure to low from place to place and its variation is the pressure, setting the air in motion. You already primary cause of air motion, i.e. wind which know that air in horizontal motion is wind. moves from high pressure areas to low Atmospheric pressure also determines when pressure areas. the air will rise or sink. The wind redistributes the heat and moisture across the planet, Vertical Variation of Pressure thereby, maintaining a constant temperature In the lower atmosphere the pressure for the planet as a whole. The vertical rising of decreases rapidly with height. The decrease moist air cools it down to form the clouds and amounts to about 1 mb for each 10 m bring precipitation. This chapter has been increase in elevation. It does not always devoted to explain the causes of pressure decrease at the same rate. Table 10.1 gives differences, the forces that control the the average pressure and temperature at atmospheric circulation, the turbulent pattern selected levels of elevation for a standard of wind, the formation of air masses, the atmosphere.
    [Show full text]
  • Baroclinic Instability, Lecture 19
    19. Baroclinic Instability In two-dimensional barotropic flow, there is an exact relationship between mass 2 streamfunction ψ and the conserved quantity, vorticity (η)given by η = ∇ ψ.The evolution of the conserved variable η in turn depends only on the spatial distribution of η andonthe flow, whichisd erivable fromψ and thus, by inverting the elliptic relation, from η itself. This strongly constrains the flow evolution and allows one to think about the flow by following η around and inverting its distribution to get the flow. In three-dimensional flow, the vorticity is a vector and is not in general con­ served. The appropriate conserved variable is the potential vorticity, but this is not in general invertible to find the flow, unless other constraints are provided. One such constraint is geostrophy, and a simple starting point is the set of quasi-geostrophic equations which yield the conserved and invertible quantity qp, the pseudo-potential vorticity. The same dynamical processes that yield stable and unstable Rossby waves in two-dimensional flow are responsible for waves and instability in three-dimensional baroclinic flow, though unlike the barotropic 2-D case, the three-dimensional dy­ namics depends on at least an approximate balance between the mass and flow fields. 97 Figure 19.1 a. The Eady model Perhaps the simplest example of an instability arising from the interaction of Rossby waves in a baroclinic flow is provided by the Eady Model, named after the British mathematician Eric Eady, who published his results in 1949. The equilibrium flow in Eady’s idealization is illustrated in Figure 19.1.
    [Show full text]
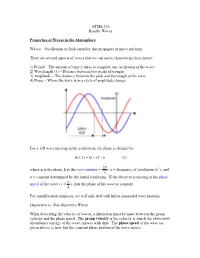
  • ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves
    ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves – Oscillations in field variables that propagate in space and time. There are several aspects of waves that we can use to characterize their nature: 1) Period – The amount of time it takes to complete one oscillation of the wave\ 2) Wavelength (λ) – Distance between two peaks of troughs 3) Amplitude – The distance between the peak and the trough of the wave 4) Phase – Where the wave is in a cycle of amplitude change For a 1-D wave moving in the x-direction, the phase is defined by: φ ),( = −υtkxtx − α (1) 2π where φ is the phase, k is the wave number = , υ = frequency of oscillation (s-1), and λ α = constant determined by the initial conditions. If the observer is moving at the phase υ speed of the wave ( c ≡ ), then the phase of the wave is constant. k For simplification purposes, we will only deal with linear sinusoidal wave motions. Dispersive vs. Non-dispersive Waves When describing the velocity of waves, a distinction must be made between the group velocity and the phase speed. The group velocity is the velocity at which the observable disturbance (energy of the wave) moves with time. The phase speed of the wave (as given above) is how fast the constant phase portion of the wave moves. A dispersive wave is one in which the pattern of the wave changes with time. In dispersive waves, the group velocity is usually different than the phase speed. A non- dispersive wave is one in which the patterns of the wave do not change with time as the wave propagates (“rigid” wave).
    [Show full text]
  • TTL Upwelling Driven by Equatorial Waves
    TTL Upwelling driven by Equatorial Waves L09804 LIUWhat drives the annual cycle in TTL upwelling? ET AL.: START OF WATER VAPOR AND CO TAPE RECORDERS L09804 Liu et al. (2007) Ortland, D. and M. J. Alexander, The residual mean circula8on in the TTL driven by tropical waves, JAS, (in review), 2013. Figure 1. (a) Seasonal variation of 10°N–10°S mean EOS MLS water vapor after dividing by the mean value at each level. (b) Seasonal variation of 10°N–10°S EOS MLS CO after dividing by the mean value at each level. represented in two principal ways. The first is by the area of [8]ConcentrationsofwatervaporandCOnearthe clouds with low infrared brightness temperatures [Gettelman tropical tropopause are available from retrievals of EOS et al.,2002;Massie et al.,2002;Liu et al.,2007].Thesecond MLS measurements [Livesey et al.,2005,2006].Monthly is by the area of radar echoes reaching the tropopause mean water vapor and CO mixing ratios at 146 hPa and [Alcala and Dessler,2002;Liu and Zipser, 2005]. In this 100 hPa in the 10°N–10°Sand10° longitude boxes are study, we examine the areas of clouds that have TRMM calculated from one full year (2005) of version 1.5 MLS Visible and Infrared Scanner (VIRS) 10.8 mmbrightness retrievals. In this work, all MLS data are processed with temperatures colder than 210 K, and the area of 20 dBZ requirements described by Livesey et al. [2005]. Tropopause echoes at 14 km measured by the TRMM Precipitation temperature is averaged from the 2.5° resolution NCEP Radar (PR).
    [Show full text]
  • Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect Along Western Boundaries with Bottom Topography and Dissipation
    JANUARY 2020 W I S E E T A L . 217 Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect along Western Boundaries with Bottom Topography and Dissipation ANTHONY WISE National Oceanography Centre, and Department of Earth, Ocean and Ecological Sciences, University of Liverpool, Liverpool, United Kingdom CHRIS W. HUGHES Department of Earth, Ocean and Ecological Sciences, University of Liverpool, and National Oceanography Centre, Liverpool, United Kingdom JEFF A. POLTON AND JOHN M. HUTHNANCE National Oceanography Centre, Liverpool, United Kingdom (Manuscript received 5 April 2019, in final form 29 October 2019) ABSTRACT Coastal trapped waves (CTWs) carry the ocean’s response to changes in forcing along boundaries and are important mechanisms in the context of coastal sea level and the meridional overturning circulation. Motivated by the western boundary response to high-latitude and open-ocean variability, we use a linear, barotropic model to investigate how the latitude dependence of the Coriolis parameter (b effect), bottom topography, and bottom friction modify the evolution of western boundary CTWs and sea level. For annual and longer period waves, the boundary response is characterized by modified shelf waves and a new class of leaky slope waves that propagate alongshore, typically at an order slower than shelf waves, and radiate short Rossby waves into the interior. Energy is not only transmitted equatorward along the slope, but also eastward into the interior, leading to the dissipation of energy locally and offshore. The b effectandfrictionresultinshelfandslope waves that decay alongshore in the direction of the equator, decreasing the extent to which high-latitude variability affects lower latitudes and increasing the penetration of open-ocean variability onto the shelf—narrower conti- nental shelves and larger friction coefficients increase this penetration.
    [Show full text]
  • The Counter-Propagating Rossby-Wave Perspective on Baroclinic Instability
    Q. J. R. Meteorol. Soc. (2005), 131, pp. 1393–1424 doi: 10.1256/qj.04.22 The counter-propagating Rossby-wave perspective on baroclinic instability. Part III: Primitive-equation disturbances on the sphere 1∗ 2 1 3 CORE By J. METHVEN , E. HEIFETZ , B. J. HOSKINS and C. H. BISHOPMetadata, citation and similar papers at core.ac.uk 1 Provided by Central Archive at the University of Reading University of Reading, UK 2Tel-Aviv University, Israel 3Naval Research Laboratories/UCAR, Monterey, USA (Received 16 February 2004; revised 28 September 2004) SUMMARY Baroclinic instability of perturbations described by the linearized primitive equations, growing on steady zonal jets on the sphere, can be understood in terms of the interaction of pairs of counter-propagating Rossby waves (CRWs). The CRWs can be viewed as the basic components of the dynamical system where the Hamil- tonian is the pseudoenergy and each CRW has a zonal coordinate and pseudomomentum. The theory holds for adiabatic frictionless flow to the extent that truncated forms of pseudomomentum and pseudoenergy are globally conserved. These forms focus attention on Rossby wave activity. Normal mode (NM) dispersion relations for realistic jets are explained in terms of the two CRWs associated with each unstable NM pair. Although derived from the NMs, CRWs have the conceptual advantage that their structure is zonally untilted, and can be anticipated given only the basic state. Moreover, their zonal propagation, phase-locking and mutual interaction can all be understood by ‘PV-thinking’ applied at only two ‘home-bases’— potential vorticity (PV) anomalies at one home-base induce circulation anomalies, both locally and at the other home-base, which in turn can advect the PV gradient and modify PV anomalies there.
    [Show full text]