DOCSLIB.ORG

MTH 303: Real Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
MTH 303: Real Analysis MTH 303: Real Analysis Semester 1, 2013-14 1. Real numbers 1.1. Decimal and ternary expansion of real numbers. (i) [0; 1] and R are uncountable. (ii) Cantor set is an uncounbtable set of measure zero. 1.2. Order properties of real numbers. (i) Least upper bound axiom. (ii) Every subset of R that has a lower bound also has a greatest lower bound. (iii) Archimedean property. (iv) Density of Q. 2. Sequences of real numbers 2.1. Limits of sequences. (i) Sequences and their limits with examples. (ii) A sequence in R has at most one limit. (iii) A sequence converges if and only if its tail converges. (iv) Let (xn) be a sequence of real numbers and let x 2 R. If (an) is a sequence of positive reals with lim(an) = 0 and if we have a constant C > 0 and some m 2 N such that jxn − xj ≤ Can, for n ≥ m, then lim(xn) = x. 2.2. Limit Therorems. (i) Bounded sequences with examples. (ii) A convergent sequence of real numbers is bounded. (iii) Convergence of the sum, difference, product, and quotient of sequences. (iv) The limit of a non-negative sequence is non-negative. (v) Squeeze Theorem: Suppose that X = (xn), Y = (yn), and Z = (zn) are sequences such that xn ≤ yn ≤ zn, 8 n, and lim(xn) = lim(zn). Then Y converges and lim(xn) = lim(yn) = lim(zn). (vi) Let X = (x ) be a sequence of positive reals such that L = lim xn+1 . n xn If L < 1, then X converges and lim(xn) = 0. 1 2 2.3. Monotone Sequences. (i) Monotone sequences with examples. (ii) Monotone Covergence Theorem: A sequence of real numbers is conver- gent if and only if it is bounded. Moreover, (a) If X = (xn) is a bounded increasing sequence, then lim(xn) = supfxn j n 2 Ng. (b) If Y = (yn) is a bounded decreasing sequence, then lim(yn) = inffyn j n 2 Ng. 2.4. Subsequences. (i) Subsequences with examples. 0 (ii) If a sequence X = (xn) converges to x, then any subsequence X = (xnk) of X also converges to x. (iii) Divergence Criteria: If a sequence X = (xn) of real numbershas either of the two properties, then X is divergent. (a) X has 2 convergent subsequences converging to different limits. (b) X is unbounded. (iv) Monotone Subsequence Theorem: If X = (xn) is a sequence of real numbers , them there exists a subsequence of X that is monotone. (v) Bolzano-Weierstrass Theorem: Every bounded sequence of real numbers has a convergent subsequence. (vi) If X = (xn) is a bounded sequence of reals such that every subsequence of X converges to x 2 R, the X converges to x. 2.5. The Cauchy Criterion. (i) Cauchy sequences with examples. (ii) Every convergent sequence is Cauchy. (iii) Every Cauchy sequence is bounded. (iv) Completeness property: Every Cauchy sequence is convergent. (v) Contractive sequences. (vi) Every contractive sequence is Cauchy. 2.6. Properly divergent sequences. (i) Properly divergent sequences with examples. (ii) A monotone sequence of real numbers is properly divergent if and only if it is unbounded (iii) Let (xn) and (yn) be sequences such that xn ≤ yn, for all n. (a) If lim(xn) = +1, then lim(yn) = +1. 3 (b) If lim(yn) = −∞, then lim(xn) = +1. (iv) Let (xn) and (yn) be sequences of positive real numbers such that lim(xn=yn) = L, for some L > 0. Then lim(xn) = +1 if and only if lim(yn) = +1. 2.7. Limit inferior and superior. (i) Subsequence limit (ii) Limit inferior and superior (iii) A bounded sequence (xn) is convergent if and only if lim sup(xn) = lim inf(xn). 3. Sequences of functions 3.1. Pointwise and uniform convergence. (i) Pointwise convergent sequences with examples. (ii) Uniformly convergent sequence with examples. (iii) Criterion for non-uniform convergence. (iv) The uniform norm k kA. (v) A sequence (fn) of bounded functions on A ⊆ R converges uniformly on A to f if and only if kfn − fkA ! 0. (vi) Cauchy criterion for uniform convergence: A sequence of bounded functions on A ⊆ R converges uniformly on A to a bounded function f if and only for each > 0 there exists a number K 2 N such that for all m; n ≥ K, then kfm − fnkA ≤ . (vii) Uniform Limit Theorem: Let (fn) be a sequence of continuous function on a set A ⊆ R such that fn converges to f uniformly on A to a function f. Then f is continuous on A. (viii) Interchange of limit and derivative: Let (fn) be a sequence of functions on a bounded interval J ⊂ R. Suppose that fn converges pointwise at 0 x0 2 J and that (fn) exists on J and converges uniformly to a function 0 g. Then (fn) converges uniformly on J to a function f such that f = g. (ix) Compactness in R. (x) Dini's Theorem: if (fn) is a sequence of continuous functions on [a; b] that converges on [a; b] to a continuous function f. Then the conver- gence of the sequence is uniform. 3.2. The metric space C[a; b]. (i) Brief introduction to metric spaces and norms. (ii) The supremum norm and the metric it induces in C[a; b]. 4 (iii) Convergence with respect to the supremum norm is equivalent to uniform convergence. (iv)C[ a; b] is complete. (v) Boundedness and total boundedness in metric spaces. (vi) A totally bounded subset of a metric space is bounded. (vii) -dense subsets of a metric space. (viii) A subset A of metric space (X; d) is totally bounded if and only if for every > 0, there exists a finite subset of A that is -dense in A. (ix) A subset A of a metric space (X; d) is totally bounded if and only if every sequence in A has a Cauchy subsequence. (x) Equicontinuous families of functions. (xi) Ascoli-Arzela Theorem: Let F be a bounded equicontinuous subset of the metric space C[a; b]. Then F is totally bounded. (xii) Every bounded equicontinuous sequence of functions in C[a; b] has a uniformly convergent subsequence. (xiii) Weierstrass Approximation Theorem: Let f be any function in C[a; b]. Then given > 0, there exists a polynomial P such that kP − fk < . In other words, the set P of polynomials is dense in C[a; b]. 4. Series of functions 4.1. Convergence and uniform convergence of a series of functions. (i) Convergence and uniform convergence with examples. (ii) Uniform Limit Theorem: Let (fn) be a sequence of real-valed function P1 on a metric space X. If n=1 fn converges uniformly to f on X and if each fn is continous at a 2 X, then f is also continuous at X. P1 (iii) Weierstrass M-test: Let n=1 fn be a series of real-valued functions on a set E. If there exists a sequence (Mn) of positive real numbers P1 P1 P1 with k=1 Mk < 1 such that k=1 fk(x) k=1 Mk, for all x 2 E, P1 then k=1 fk converges uniformly on E. P1 k (iv) If the power series k=0 akx coverges for x = x0, then it converges uniformly on [−a; a], where a is any number such that 0 < a < jx0j. P1 (v) Dini's Theorem: Let n=1 fn be a series of continuous nonnegative P1 functions on the a compact metric space X. If n=1 fn converges on X to the continuous function f, then the convergence is uniform on X. 4.2. Taylor's Theorem. (i) Taylor series with examples. 5 (ii) Taylor's Theorem (with intergal form of remainder): Let f be a real valued function on [a; a + h] such that f (n+1)(x) exists for every x 2 [a; a + h] and f (n+1) is continuous in [a; a + h]. Then f 0(a) f 00(a) f(x) = f(a) + (x − a) + (x − a)2 + ::: 1! 2! f (n)(a) + (x − a)n + R (x 2 [a; a + h]); n! n+1 where Z x 1 n (n+1) Rn+1 = (x − t) f (t) dt : n! a (iii) Taylor's Theorem (with Lagrange form of remainder): Let f be a real valued function on [a; a + h] such that f (n+1)(x) exists for every x 2 [a; a+h] and f (n+1) is continuous in [a; a+h]. Then if x 2 [a; a+h], there exists a number c 2 [a; x] such that f 0(a) f 00(a) f (n)(a) f(x) = f(a) + (x − a) + (x − a)2 + ::: + (x − a)n 1! 2! n! f (n+1)(c) + (x − a)n+1: (n + 1)! (iv) Taylor's Theorem (with Cauchy form of remainder): Let f be a real valued function on [a; a + h] such that f (n+1)(x) exists for every x 2 [a; a + h] and f (n+1) is continuous in [a; a + h]. Then if x 2 [a; a + h], there exists a number c 2 [a; x] such that f 0(a) f 00(a) f (n)(a) f(x) = f(a) + (x − a) + (x − a)2 + ::: + (x − a)n 1! 2! n! f (n+1)(c) + (x − c)n(x − a): n! (v) The series expansions for the elementary functions log(1 + h) and ex. 5. Functions of bounded variation 5.1. Properties of monotonic functions. (i) Let f be an increasing function defined on [a; b] and let and let P = fx0; x1; : : : ; xng be a partition of [a; b].
Load more

Recommended publications
  • Vector Measures with Variation in a Banach Function Space
    VECTOR MEASURES WITH VARIATION IN A BANACH FUNCTION SPACE O. BLASCO Departamento de An´alisis Matem´atico, Universidad de Valencia, Doctor Moliner, 50 E-46100 Burjassot (Valencia), Spain E-mail:[email protected] PABLO GREGORI Departament de Matem`atiques, Universitat Jaume I de Castell´o, Campus Riu Sec E-12071 Castell´o de la Plana (Castell´o), Spain E-mail:[email protected] Let E be a Banach function space and X be an arbitrary Banach space. Denote by E(X) the K¨othe-Bochner function space defined as the set of measurable functions f :Ω→ X such that the nonnegative functions fX :Ω→ [0, ∞) are in the lattice E. The notion of E-variation of a measure —which allows to recover the p- variation (for E = Lp), Φ-variation (for E = LΦ) and the general notion introduced by Gresky and Uhl— is introduced. The space of measures of bounded E-variation VE (X) is then studied. It is shown, amongother thingsand with some restriction ∗ ∗ of absolute continuity of the norms, that (E(X)) = VE (X ), that VE (X) can be identified with space of cone absolutely summingoperators from E into X and that E(X)=VE (X) if and only if X has the RNP property. 1. Introduction The concept of variation in the frame of vector measures has been fruitful in several areas of the functional analysis, such as the description of the duality of vector-valued function spaces such as certain K¨othe-Bochner function spaces (Gretsky and Uhl10, Dinculeanu7), the reformulation of operator ideals such as the cone absolutely summing operators (Blasco4), and the Hardy spaces of harmonic function (Blasco2,3).
    [Show full text]
  • Chapter 4 the Lebesgue Spaces
    Chapter 4 The Lebesgue Spaces In this chapter we study Lp-integrable functions as a function space. Knowledge on functional analysis required for our study is briefly reviewed in the first two sections. In Section 1 the notions of normed and inner product spaces and their properties such as completeness, separability, the Heine-Borel property and espe- cially the so-called projection property are discussed. Section 2 is concerned with bounded linear functionals and the dual space of a normed space. The Lp-space is introduced in Section 3, where its completeness and various density assertions by simple or continuous functions are covered. The dual space of the Lp-space is determined in Section 4 where the key notion of uniform convexity is introduced and established for the Lp-spaces. Finally, we study strong and weak conver- gence of Lp-sequences respectively in Sections 5 and 6. Both are important for applications. 4.1 Normed Spaces In this and the next section we review essential elements of functional analysis that are relevant to our study of the Lp-spaces. You may look up any book on functional analysis or my notes on this subject attached in this webpage. Let X be a vector space over R. A norm on X is a map from X ! [0; 1) satisfying the following three \axioms": For 8x; y; z 2 X, (i) kxk ≥ 0 and is equal to 0 if and only if x = 0; (ii) kαxk = jαj kxk, 8α 2 R; and (iii) kx + yk ≤ kxk + kyk. The pair (X; k·k) is called a normed vector space or normed space for short.
    [Show full text]
  • Symmetric Rigidity for Circle Endomorphisms with Bounded Geometry
    SYMMETRIC RIGIDITY FOR CIRCLE ENDOMORPHISMS WITH BOUNDED GEOMETRY JOHN ADAMSKI, YUNCHUN HU, YUNPING JIANG, AND ZHE WANG Abstract. Let f and g be two circle endomorphisms of degree d ≥ 2 such that each has bounded geometry, preserves the Lebesgue measure, and fixes 1. Let h fixing 1 be the topological conjugacy from f to g. That is, h ◦ f = g ◦ h. We prove that h is a symmetric circle homeomorphism if and only if h = Id. Many other rigidity results in circle dynamics follow from this very general symmetric rigidity result. 1. Introduction A remarkable result in geometry is the so-called Mostow rigidity theorem. This result assures that two closed hyperbolic 3-manifolds are isometrically equivalent if they are homeomorphically equivalent [18]. A closed hyperbolic 3-manifold can be viewed as the quotient space of a Kleinian group acting on the open unit ball in the 3-Euclidean space. So a homeomorphic equivalence between two closed hyperbolic 3-manifolds can be lifted to a homeomorphism of the open unit ball preserving group actions. The homeomorphism can be extended to the boundary of the open unit ball as a boundary map. The boundary is the Riemann sphere and the boundary map is a quasi-conformal homeomorphism. A quasi-conformal homeomorphism of the Riemann 2010 Mathematics Subject Classification. Primary: 37E10, 37A05; Secondary: 30C62, 60G42. Key words and phrases. quasisymmetric circle homeomorphism, symmetric cir- arXiv:2101.06870v1 [math.DS] 18 Jan 2021 cle homeomorphism, circle endomorphism with bounded geometry preserving the Lebesgue measure, uniformly quasisymmetric circle endomorphism preserving the Lebesgue measure, martingales.
    [Show full text]
  • Generalizations of the Riemann Integral: an Investigation of the Henstock Integral
    Generalizations of the Riemann Integral: An Investigation of the Henstock Integral Jonathan Wells May 15, 2011 Abstract The Henstock integral, a generalization of the Riemann integral that makes use of the δ-fine tagged partition, is studied. We first consider Lebesgue’s Criterion for Riemann Integrability, which states that a func- tion is Riemann integrable if and only if it is bounded and continuous almost everywhere, before investigating several theoretical shortcomings of the Riemann integral. Despite the inverse relationship between integra- tion and differentiation given by the Fundamental Theorem of Calculus, we find that not every derivative is Riemann integrable. We also find that the strong condition of uniform convergence must be applied to guarantee that the limit of a sequence of Riemann integrable functions remains in- tegrable. However, by slightly altering the way that tagged partitions are formed, we are able to construct a definition for the integral that allows for the integration of a much wider class of functions. We investigate sev- eral properties of this generalized Riemann integral. We also demonstrate that every derivative is Henstock integrable, and that the much looser requirements of the Monotone Convergence Theorem guarantee that the limit of a sequence of Henstock integrable functions is integrable. This paper is written without the use of Lebesgue measure theory. Acknowledgements I would like to thank Professor Patrick Keef and Professor Russell Gordon for their advice and guidance through this project. I would also like to acknowledge Kathryn Barich and Kailey Bolles for their assistance in the editing process. Introduction As the workhorse of modern analysis, the integral is without question one of the most familiar pieces of the calculus sequence.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
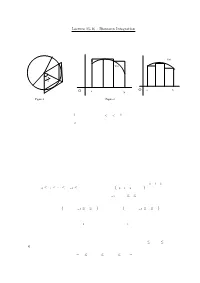
  • Lecture 15-16 : Riemann Integration Integration Is Concerned with the Problem of finding the Area of a Region Under a Curve
    1 Lecture 15-16 : Riemann Integration Integration is concerned with the problem of ¯nding the area of a region under a curve. Let us start with a simple problem : Find the area A of the region enclosed by a circle of radius r. For an arbitrary n, consider the n equal inscribed and superscibed triangles as shown in Figure 1. f(x) f(x) π 2 n O a b O a b Figure 1 Figure 2 Since A is between the total areas of the inscribed and superscribed triangles, we have nr2sin(¼=n)cos(¼=n) · A · nr2tan(¼=n): By sandwich theorem, A = ¼r2: We will use this idea to de¯ne and evaluate the area of the region under a graph of a function. Suppose f is a non-negative function de¯ned on the interval [a; b]: We ¯rst subdivide the interval into a ¯nite number of subintervals. Then we squeeze the area of the region under the graph of f between the areas of the inscribed and superscribed rectangles constructed over the subintervals as shown in Figure 2. If the total areas of the inscribed and superscribed rectangles converge to the same limit as we make the partition of [a; b] ¯ner and ¯ner then the area of the region under the graph of f can be de¯ned as this limit and f is said to be integrable. Let us de¯ne whatever has been explained above formally. The Riemann Integral Let [a; b] be a given interval. A partition P of [a; b] is a ¯nite set of points x0; x1; x2; : : : ; xn such that a = x0 · x1 · ¢ ¢ ¢ · xn¡1 · xn = b.
    [Show full text]
  • Bounded Holomorphic Functions of Several Variables
    Bounded holomorphic functions of several variables Gunnar Berg Introduction A characteristic property of holomorphic functions, in one as well as in several variables, is that they are about as "rigid" as one can demand, without being iden- tically constant. An example of this rigidity is the fact that every holomorphic function element, or germ of a holomorphic function, has associated with it a unique domain, the maximal domain to which the function can be continued. Usually this domain is no longer in euclidean space (a "schlicht" domain), but lies over euclidean space as a many-sheeted Riemann domain. It is now natural to ask whether, given a domain, there is a holomorphic func- tion for which it is the domain of existence, and for domains in the complex plane this is always the case. This is a consequence of the Weierstrass product theorem (cf. [13] p. 15). In higher dimensions, however, the situation is different, and the domains of existence, usually called domains of holomorphy, form a proper sub- class of the class of aU domains, which can be characterised in various ways (holo- morphic convexity, pseudoconvexity etc.). To obtain a complete theory it is also in this case necessary to consider many-sheeted domains, since it may well happen that the maximal domain to which all functions in a given domain can be continued is no longer "schlicht". It is possible to go further than this, and ask for quantitative refinements of various kinds, such as: is every domain of holomorphy the domain of existence of a function which satisfies some given growth condition? Certain results in this direction have been obtained (cf.
    [Show full text]
  • Riesz-Fredhölm Theory
    Riesz-Fredh¨olmTheory T. Muthukumar [email protected] Contents 1 Introduction1 2 Integral Operators1 3 Compact Operators7 4 Fredh¨olmAlternative 14 Appendices 18 A Ascoli-Arzel´aResult 18 B Normed Spaces and Bounded Operators 20 1 Introduction The aim of this lecture note is to show the existence and uniqueness of Fredh¨olmintegral operators of second kind, i.e., show the existence of a solution x of x − T x = y for any given y, in appropriate function spaces. 2 Integral Operators Let E be a compact subset of Rn and C(E) denote the space of complex valued continuous functions on E endowed with the uniform norm kfk1 = supx2E jf(x)j. Recall that C(E) is a Banach space with the uniform norm. 1 Definition 2.1. Any continuous function K : E × E ! C is called a con- tinuous kernel. Since K is continuous on a compact set, K is both bounded, i.e., there is a κ such that jK(x; y)j ≤ κ 8x; y 2 E and uniformly continuous. In particular, for each " > 0 there is a δ > 0 such that jK(x1; y) − K(x2; y)j ≤ " 8y 2 E whenever jx1 − x2j < δ. Example 2.1 (Fredh¨olmintegral operator). For any f 2 C(E), we define Z T (f)(x) = K(x; y)f(y) dy E where x 2 E and K : E × E ! R is a continuous function. For each " > 0, Z jT f(x1) − T f(x2)j ≤ jK(x1; y) − K(x2; y)jjf(y)j dy ≤ "kfk1jEj E whenever jx1 − x2j < δ.
    [Show full text]
  • Chapter 2. Functions of Bounded Variation §1. Monotone Functions
    Chapter 2. Functions of Bounded Variation §1. Monotone Functions Let I be an interval in IR. A function f : I → IR is said to be increasing (strictly increasing) if f(x) ≤ f(y)(f(x) < f(y)) whenever x, y ∈ I and x < y. A function f : I → IR is said to be decreasing (strictly decreasing) if f(x) ≥ f(y)(f(x) > f(y)) whenever x, y ∈ I and x < y. A function f : I → IR is said to be monotone if f is either increasing or decreasing. In this section we will show that a monotone function is differentiable almost every- where. For this purpose, we first establish Vitali covering lemma. Let E be a subset of IR, and let Γ be a collection of closed intervals in IR. We say that Γ covers E in the sense of Vitali if for each δ > 0 and each x ∈ E, there exists an interval I ∈ Γ such that x ∈ I and `(I) < δ. Theorem 1.1. Let E be a subset of IR with λ∗(E) < ∞ and Γ a collection of closed intervals that cover E in the sense of Vitali. Then, for given ε > 0, there exists a finite disjoint collection {I1,...,IN } of intervals in Γ such that ∗ N λ E \ ∪n=1In < ε. Proof. Let G be an open set containing E such that λ(G) < ∞. Since Γ is a Vitali covering of E, we may assume that each I ∈ Γ is contained in G. We choose a sequence (In)n=1,2,... of disjoint intervals from Γ recursively as follows.
    [Show full text]
  • Section 3.5 of Folland’S Text, Which Covers Functions of Bounded Variation on the Real Line and Related Topics
    REAL ANALYSIS LECTURE NOTES: 3.5 FUNCTIONS OF BOUNDED VARIATION CHRISTOPHER HEIL 3.5.1 Definition and Basic Properties of Functions of Bounded Variation We will expand on the first part of Section 3.5 of Folland's text, which covers functions of bounded variation on the real line and related topics. We begin with functions defined on finite closed intervals in R (note that Folland's ap- proach and notation is slightly different, as he begins with functions defined on R and uses TF (x) instead of our V [f; a; b]). Definition 1. Let f : [a; b] ! C be given. Given any finite partition Γ = fa = x0 < · · · < xn = bg of [a; b], set n SΓ = jf(xi) − f(xi−1)j: i=1 X The variation of f over [a; b] is V [f; a; b] = sup SΓ : Γ is a partition of [a; b] : The function f has bounded variation on [a; b] if V [f; a; b] < 1. We set BV[a; b] = f : [a; b] ! C : f has bounded variation on [a; b] : Note that in this definition we are considering f to be defined at all poin ts, and not just to be an equivalence class of functions that are equal a.e. The idea of the variation of f is that is represents the total vertical distance traveled by a particle that moves along the graph of f from (a; f(a)) to (b; f(b)). Exercise 2. (a) Show that if f : [a; b] ! C, then V [f; a; b] ≥ jf(b) − f(a)j.
    [Show full text]
  • Measure Algebras and Functions of Bounded Variation on Idempotent Semigroupso
    TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 163, January 1972 MEASURE ALGEBRAS AND FUNCTIONS OF BOUNDED VARIATION ON IDEMPOTENT SEMIGROUPSO BY STEPHEN E. NEWMAN Abstract. Our main result establishes an isomorphism between all functions on an idempotent semigroup S with identity, under the usual addition and multiplication, and all finitely additive measures on a certain Boolean algebra of subsets of S, under the usual addition and a convolution type multiplication. Notions of a function of bounded variation on 5 and its variation norm are defined in such a way that the above isomorphism, restricted to the functions of bounded variation, is an isometry onto the set of all bounded measures. Our notion of a function of bounded variation is equivalent to the classical notion in case S is the unit interval and the "product" of two numbers in S is their maximum. 1. Introduction. This paper is motivated by the pair of closely related Banach algebras described below. The interval [0, 1] is an idempotent semigroup when endowed with the operation of maximum multiplication (.vj = max (x, y) for all x, y in [0, 1]). We let A denote the Boolean algebra (or set algebra) consisting of all finite unions of left-open, right-closed intervals (including the single point 0) contained in the interval [0, 1]. The space M(A) of all bounded, finitely additive measures on A is a Banach space with the usual total variation norm. The nature of the set algebra A and the idempotent multiplication given the interval [0, 1] make it possible to define a convolution multiplication in M(A) which makes it a Banach algebra.
    [Show full text]
  • On the Convolution of Functions of Λp – Bounded Variation and a Locally
    IOSR Journal of Mathematics (IOSR-JM) e-ISSN: 2278-5728,p-ISSN: 2319-765X, Volume 8, Issue 3 (Sep. - Oct. 2013), PP 70-74 www.iosrjournals.org On the Convolution of Functions of p – Bounded Variation and a Locally Compact Hausdorff Topological Group S. M. Nengem1, D. Samaila1 and M. Solomon1 1 Department of Mathematical Sciences, Adamawa State University, P. M. B. 25, Mubi, Nigeria Abstract: The smoothness-increasing operator “convolution” is well known for inheriting the best properties of each parent function. It is also well known that if f L1 and g is a Bounded Variation (BV) function, then f g inherits the properties from the parent’s spaces. This aspect of BV can be generalized in many ways and many generalizations are obtained. However, in this paper we introduce the notion of p – Bounded variation function. In relation to that we show that the convolution of two functions f g is the inverse Fourier transforms of the two functions. Moreover, we prove that if f, g BV(p)[0, 2], then f g BV(p)[0, 2], and that on any locally compact Abelian group, a version of the convolution theorem holds. Keywords: Convolution, p-Bounded variation, Fourier transform, Abelian group. I. Introduction In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions, giving the area overlap between the two functions as a function of the amount that one of the original functions is translated.
    [Show full text]