Computation of Flow and Bed Morphology at River Confluences
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Amazon River Voyage
AMAZON RIVER VOYAGE Over the 38 years that International Expeditions has been leading Amazon River cruises, our guests have enjoyed unrivaled access to the Peruvian rainforest’s most pristine areas and the company of the river’s most knowledgeable guides. Your exciting daily excursions include birding at dawn, school visits in local villages and even piranha fishing! Join IE and be transported to the Amazon of your imagination to discover a rainforest that pulsates with an unrivaled diversity of wildlife. Authentic Amazon River Experience Aboard this luxury Amazon River cruise, you’ll create a lifetime of memories: the joy in the eyes of a village child when you visit their school; the enveloping darkness of the jungle; or the awe possible. of floating along narrow streams accompanied by pink dolphins. Drawing on insight from our native Amazon travel guides, Explore with Pioneers in Amazon Travel International Expeditions intentionally varies the villages and International Expeditions pioneered travel to the Peruvian tributaries we visit, ensuring you get the most authentic Amazon, and our nature-focused, small-group expedition travel rainforest tour experience remains the standard for Amazon Voyage expedition cruises. IE not only pioneered travel to this region, we still work with many of the naturalist guides that we helped to train. Ensuring a worry-free and educational journey, these expert local naturalist guides — along with an expedition leader — accompany our Amazon Voyage cruises. Each day, these knowledgeable Amazon River travel guides use their decades of learning and guiding experience to serve as lecturers, field guides and friends as you explore the rainforest. -

The Cedar River
Since the 1800’s, Iowa rivers have been designated as CEDARCEDAR either meandered or non- RIVERRIVER meandered. Much of the Cedar River Water Trail is lined with public lands and classified as meandered, meaning that BLACK HAWK COUNTY paddlers may access not only BLACK HAWK the river itself but also the COUNTY river bottom and banks along its course. However, north of Washington Park, the river is classified as non-meandered, meaning that the river bed and surrounding land are owned by the adjacent landowners and paddlers should respect their property rights. BLACK HAWK COUNTY THE CEDAR RIVER - WILDNESS AND CIVILIZATION The Cedar River Water Trail offers a unique paddling experience amongst Iowa’s designated water trails. A journey down the 47 miles of the trail features dramatically contrasting settings, with the wildness of forested bottomlands rich with diverse plant, wildlife, and bird species giving way to historic urban environments. Paddlers are offered an opportunity to explore the downtowns of two major Iowa cities before returning again to the river’s pastoral setting. Traversing the county’s widest stream, its landscape, and lore may feel like time travel at times. From prehistoric times into the present, the Silver maples shade a peaceful backwater of the Cedar River Cedar River valley continues to beckon These trees, typical of bottomland hardwood forest, often grow right up to the water’s to paddlers to explore its natural beauty edge. Quiet back channels are “nurseries” for aquatic wildlife and isolated nesting areas for and cultural treasures. birds and wildlife. Red-spotted purple butterfly Bank swallow nest holes Cedar waxwing gathering nest material CEDAR RIVER WATER TRAIL The Cedar River bisects Black Hawk County diagonally as it continues to erode the landform region called the Iowan Surface. -

Community Report
Community Report Dear Friends, As we refl ect on 2019 so far and look forward to the rest of the Our Mission year, I am thankful for all of those who give their time and talents to make Confl uence Health a place I am proud to be a part of We are dedicated to improving our patients’ every day. Our vision states that Confl uence Health strives “to health by providing safe, high-quality care in become the highest value rural health care system in the nation,” a compassionate and cost-effective manner. About Us and that goal isn’t achieved by accident. Our success is directly impacted by the dedication of our exceptional physicians, nurses, employees, volunteers and leadership teams, who all share a commitment to our patients. Healthy individuals make Our Vision healthy communities, and we understand and embrace the part we play in making that a reality. To become the highest value rural health 4, 000+ employees care system in the nation that improves Additionally, fulfi lling this vision means ensuring the best possible health, quality of life, and is a source of health outcomes at the lowest possible cost, whenever and wherever our patients need care. If we can accomplish that, pride to those who work here. we will uphold our founding principle that a locally controlled, 12 cities directed and integrated health care delivery system best meets the needs of this region. While acknowledging our successes, we understand there is still 12,000 much to do to ensure our community receives the effective and square mile timely care it deserves. -

Holocene Environmental Archaeology of the Yangtze River Valley in China: a Review
land Review Holocene Environmental Archaeology of the Yangtze River Valley in China: A Review Li Wu 1,2,*, Shuguang Lu 1, Cheng Zhu 3, Chunmei Ma 3, Xiaoling Sun 1, Xiaoxue Li 1, Chenchen Li 1 and Qingchun Guo 4 1 Provincial Key Laboratory of Earth Surface Processes and Regional Response in the Yangtze-Huaihe River Basin, School of Geography and Tourism, Anhui Normal University, Wuhu 241002, China; [email protected] (S.L.); [email protected] (X.S.); [email protected] (X.L.); [email protected] (C.L.) 2 State Key Laboratory of Loess and Quaternary Geology, Institute of Earth Environment, Chinese Academy of Sciences, Xi’an 710061, China 3 School of Geograpy and Ocean Science, Nanjing University, Nanjing 210023, China; [email protected] (C.Z.); [email protected] (C.M.) 4 School of Environment and Planning, Liaocheng University, Liaocheng 252000, China; [email protected] * Correspondence: [email protected] Abstract: The Yangtze River Valley is an important economic region and one of the cradles of human civilization. It is also the site of frequent floods, droughts, and other natural disasters. Conducting Holocene environmental archaeology research in this region is of great importance when studying the evolution of the relationship between humans and the environment and the interactive effects humans had on the environment from 10.0 to 3.0 ka BP, for which no written records exist. This Citation: Wu, L.; Lu, S.; Zhu, C.; review provides a comprehensive summary of materials that have been published over the past Ma, C.; Sun, X.; Li, X.; Li, C.; Guo, Q. -

The Effect of Different Confluence Confirmation Strategies on the Obturation of Vertucci Type II Canal: Micro-CT Analysis
Restor Dent Endod. 2021 Feb;46(1):e12 https://doi.org/10.5395/rde.2021.46.e12 pISSN 2234-7658·eISSN 2234-7666 Research Article The effect of different confluence confirmation strategies on the obturation of Vertucci type II canal: micro-CT analysis Seungjae Do , Min-Seock Seo * Department of Conservative Dentistry, Wonkwang University Daejeon Dental Hospital, Daejeon, Korea Received: Apr 8, 2020 Revised: Jun 7, 2020 ABSTRACT Accepted: Jun 17, 2020 Objectives: The present study aims to compare the obturation quality of 2 confluence Do S, Seo MS confirmation techniques in artificial maxillary first premolars showing Vertucci type II root canal configuration. *Correspondence to Min-Seock Seo, DDS, PhD Materials and Methods: Thirty artificial maxillary premolars having Vertucci type II root Associate Professor, Department of canal configuration were made. They were divided into 3 groups according to the confluence Conservative Dentistry, Wonkwang University confirmation technique as follows. Gutta-percha indentation (GPI) group (confluence Daejeon Dental Hospital, 77 Dunsan-ro, Seo- confirmation using a gutta-percha cone and a K file); electronic apex locator (EAL) group gu, Daejeon 35233, Korea. (confluence confirmation using K files and EAL); and no confluence detection (NCD) E-mail: [email protected] group. In the GPI group and the EAL group, shaping and obturation were performed with Copyright © 2021. The Korean Academy of the modified working length (WL). In the NCD group, shaping was performed without WL Conservative Dentistry adjustment and obturation was carried out with an adjusted master cone. Micro-computed This is an Open Access article distributed tomography was used before preparation and after obturation to calculate the percentage under the terms of the Creative Commons of gutta-percha occupied volume (%GPv) and the volume increase in the apical 4 mm. -

Modelling Confluence Dynamics in Large Sand-Bed Braided Rivers
Earth Surf. Dynam. Discuss., https://doi.org/10.5194/esurf-2018-85 Manuscript under review for journal Earth Surf. Dynam. Discussion started: 18 December 2018 c Author(s) 2018. CC BY 4.0 License. 1 Modelling confluence dynamics in large sand-bed braided rivers 2 Haiyan Yang1, Zhenhuan Liu2 3 1College of Water Conservancy and Civil Engineering, South China Agricultural 4 University, Guangzhou 510642, China; [email protected] 5 2 Guangdong Provincial Key Laboratory of Urbanization and Geo-simulation, School 6 of Geography and Planning, Sun Yat-sen University, Guangzhou 510275, China 7 Correspondence: [email protected] 8 Abstract 9 Confluences are key morphological nodes in braided rivers where flow converges, 10 creating complex flow patterns and rapid bed deformation. Field survey and laboratory 11 experimental studies have been carried out to investigate the morphodynamic features 12 in individual confluences, but few have investigated the evolution process of 13 confluences in large braided rivers. In the current study a physics-based numerical 14 model was applied to simulate a large lowland braided river dominated by suspended 15 sediment transport, and analyzed the morphologic changes at confluences and their 16 controlling factors. It was found that the confluences in large braided rivers exhibit 17 some dynamic processes and geometric characteristics that are similar to those observed 18 in individual confluences arising from two tributaries. However, they also show some 19 unique characteristics that are result from the influence of the overall braided pattern 20 and especially of neighboring upstream channels. 21 Key words: braided river, numerical model, confluence, dynamics, geometry, scour 22 hole 1 Earth Surf. -

Fluid Mechanics, Sediment Transport and Mixing About the Confluence of Negro and Solimões Rivers, Manaus, Brazil
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Archivio della ricerca - Università degli studi di Napoli Federico II E-proceedings of the 36th IAHR World Congress 28 June – 3 July, 2015, The Hague, the Netherlands FLUID MECHANICS, SEDIMENT TRANSPORT AND MIXING ABOUT THE CONFLUENCE OF NEGRO AND SOLIMÕES RIVERS, MANAUS, BRAZIL MARK TREVETHAN(1), ANDRE MARTINELLI(2), MARCO OLIVEIRA(2), MARCO IANNIRUBERTO(3) & CARLO GUALTIERI(1) (1) Department of Civil, Construction and Environmental Engineering, University of Napoli Federico II, Napoli, Italy, [email protected]; [email protected] (2) Geological Survey of Brasil (CPRM), Manaus, Brazil, [email protected]; [email protected] (3) Institute of Geosciences, University of Brasilia, Brasilia, Brazil, [email protected] ABSTRACT As part of a project to investigate the hydrodynamic, sediment transport and mixing processes about the large confluences of the Amazon River, a field study was conducted about the confluence of the Negro and Solimões Rivers. This confluence ranks among the largest confluences on Earth the outcomes of this study may also provide some general insights into large confluence dynamics. A detailed series of ADCP, water quality and seismic profile measurements were collected to investigate key hydrodynamic and morphodynamic features about this confluence. Presented here are the key hydrodynamic features observed about this large confluence and how these relate to findings in previous studies conducted in flumes and small confluences. Finally some insights into how the differences in water characteristics and the hydrodynamics of these two rivers may influence the rate of mixing downstream are presented. -

Surface Water Types and Sediment Distribution Patterns at the Confluence of Mega Rivers: the Solimões-Amazon and Negro Rivers Junction
Surface water types and sediment distribution patterns at the confluence of mega rivers: the Solimões-Amazon and Negro rivers junction Edward Park1, Edgardo M. Latrubesse1 1University of Texas at Austin, Department of Geography and the Environment, Austin, TX, USA Correspondence to: Edward Park, Tel +1-512-230-4603 Fax +1-512-471-5049 University of Texas at Austin, SAC 4.178, 2201 Speedway, Austin, TX 78712, USA Email address: [email protected] This article has been accepted for publication and undergone full peer review but has not been through the copyediting, typesetting, pagination and proofreading process which may lead to differences between this version and the Version of Record. Please cite this article as an ‘Accepted Article’, doi: 10.1002/2014WR016757 This article is protected by copyright. All rights reserved. Abstract Large river channel confluences are recognized as critical fluvial features because both intensive and extensive hydrophysical and geoecological processes take place at this interface. However, identifications of suspended sediment routing patterns through channel junctions and the roles of tributaries on downstream sediment transport in large rivers are still poorly explored. In this paper, we propose a remote sensing-based approach to characterize the spatiotemporal patterns of the post-confluence suspended sediment transport by mapping the surface water distribution in the ultimate example of large river confluence on Earth where distinct water types meet: The Solimões-Amazon (white water) and Negro (black water) rivers. The surface water types distribution was modeled for three different years: average hydrological condition (2007) and two years when extreme events occurred (drought-2005 and flood-2009). -

Drainagebasin Characteristics
350 TRANSACTIONS, AMERICAN GEOPHYSICAL UNION DRAINAGE-BASIN CHARACTERISTICS Robert E. Horton Factors descriptive of a drainage-basin as related to its hydrology may be classi fied broadly as s (1) Morphologic—These factors depend only on the topography of the land forms of which the drainage-basin is composed and on the form and extent of the stream-system or drainage-net within It. (2) Soil factors—This group includes factors descriptive of the materials form ing the groundwork of the drainage-basin, including all those physical properties in volved in the moisture-relations of soils. (3) Geologic-structural factors—These factors relate to the depths and charac teristics of the underlying rocks and the nature of the geologic structures in so far as they are related to ground-water conditions or otherwise to the hydrology of the drainage-basin. (4) Vegetational factors—These are factors which depend wholly or in part on the vegetation, natural or cultivated, growing within the drainage-basin. (5) Climatic-hydrologic factors--Climatic factors include: Temperature, humid ity, rainfall, and evaporation, but as humidity, rainfall, and evaporation may also be considered as hydrologic, the two groups of factors have been combined. Hydrologic factors relate specially to conditions dependent on the operation of the hydrologic cycle, particularly with reference to runoff and ground-water. One of the central problems of hydrology is the correlation of the hydrologic characteristics of a drainage-basin with its morphology, soils, and vegetation. The problem is obviously complex. In some cases, as, for example, with reference to geologic structure, it is obviously difficult, if not impossible, to express the characteristics of the drainage-basin in simple, numerical terms. -

Restoration Opportunities at Tributary Confluences: Critical Habitat Assessment of the Big Chico Creek/Mud Creek/Sacramento River Confluence Area
Restoration Opportunities at Tributary Confluences: Critical Habitat Assessment of the Big Chico Creek/Mud Creek/Sacramento River Confluence Area A report to: The Nature Conservancy, Sacramento River Project1 By: Eric M. Ginney2 Bidwell Environmental Institute, California State University, Chico December 2001. 1Please direct correspondence to: TNC, Sac. River Project Attn: D. Peterson 505 Main Street, Chico CA 95928 [email protected] 2Bidwell Environmental Institute CSU, Chico, Chico, CA 95929-0555 [email protected] Cover: An abstract view of the Sacramento River, looking upstream. Big Chico Creek enters from the east, in the lower portion of the image. Photograph and image manipulation by the author. Table of Contents Section I Study Purpose, Methods, and Objectives 1 Purpose 1 Methods and Objectives 2 Section II Tributary Confluences: Restoration 3 Opportunities Waiting to Happen Ecological Importance of Tributary Confluences and 3 Adjacent Floodplain Importance of Sacramento River Confluence Areas in 5 Collaborative Restoration Efforts Conservation by Design 7 Site-Specific Planning 8 Section III Critical Habitat Identification and Analysis 10 of Physical Processes Location and Description of Study Area 10 Landscape Level 10 Historic Conditions of Study Area and Changes 10 Through Time Current Conditions and Identification of Critical Habitat 16 Hydrologic Data 16 Soils 17 Hydro-geomorphic Processes 17 Site-Level Description: Singh Orchard Parcel 18 On-The-Ground Observations: Singh Parcel 19 Critical Habitat for Species of Concern -
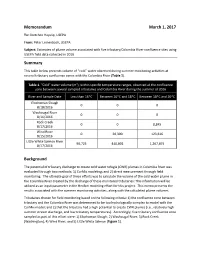
Estimates of Plume Volume Associated with Five Tributary/Columbia River Confluence Sites Using USEPA Field Data Collected in 2016
Memorandum March 1, 2017 To: Gretchen Hayslip, USEPA From: Peter Leinenbach, USEPA Subject: Estimates of plume volume associated with five tributary/Columbia River confluence sites using USEPA field data collected in 2016 Summary This table below presents volume of “cold” water observed during summer monitoring activities at several tributary confluence zones with the Columbia River (Table 1). Table 1. “Cold” water volume (m3), within specific temperature ranges, observed at the confluence zone between several sampled tributaries and Columbia River during the summer of 2016 River and Sample Date Less than 16*C Between 16*C and 18*C Between 18*C and 20*C Elochoman Slough 0 0 0 8/18/2016 Washougal River 0 0 0 8/16/2016 Rock Creek 0 0 8,845 8/17/2016 Wind River 0 20,390 123,616 8/15/2016 Little White Salmon River 90,723 440,801 1,267,874 8/17/2016 Background The potential of tributary discharge to create cold water refugia (CWR) plumes in Columbia River was evaluated through two methods: 1) CorMix modeling; and 2) direct measurement through field monitoring. The ultimate goal of these efforts was to calculate the volume of the cold water plume in the Columbia River created by the discharge of these monitored tributaries: This information will be utilized as an input parameter in the HexSim modeling effort for this project. This memo presents the results associated with the summer monitoring activities, along with the calculated plume volumes. Tributaries chosen for field monitoring based on the following criteria: 1) the confluence zone between tributary and the Colombia River was determined to be too hydrologically complex to model with the CorMix model; and 2) that the tributary had a high potential to create CWR plumes (i.e., relatively high summer stream discharge, and low tributary temperatures). -

Chapter 1. Management of Mississippi and Ohio River Landscapes
Management of Mississippi and Ohio River Landscapes wo powerful rivers, these rivers for1 navigation Tthe Ohio and Missis- and to protect communities, sippi, and their tributaries agriculture, and other high- drain more than 41% of the value land uses. Alongside attempts interior continental United States to control the height and courses of of America (map 1.1). Their shifting these rivers and their tributaries, diversion paths have shaped and reshaped the landscapes ditches and systematic draining of interior swamps through which they flow and the confluence (map 1.2) and wetlands have transformed hydric but fertile soils where their sediment-laden waters comingle on the into highly productive, intensely managed agricultural voyage to the Gulf of Mexico. Changing climates and lands. Paradoxically, these infrastructure investments, extreme weather events over the millennia have carved intended to facilitate navigation and reduce direct risks new channels through river bottomlands, leaving rock- of flooding, have led to unexpected consequences to exposed uplands and fertile valleys behind while altering the larger ecosystem. Recent levee breaching has cre- the location where the Ohio and Mississippi rivers meet. ated unanticipated shocks to the river ecosystem while These great rivers often became state boundaries, and generating new knowledge about hydrology, soils, and their historic realignments have added and subtracted the vegetation of rivers and their bottomlands. The oc- land from many states that border them. For much of casional failure of well-engineered structures reminds their history, the lands adjacent to these rivers were low- us that the river landscape is a complex human-natural lying bottomlands that, unconstrained by human struc- system.