Universal Differential Equations for Scientific Machine Learning
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PROTECTIVE CUSTODY NEEDS ASSESSMENT/\L\Fjuvier REGISTER NUMBER HOUSING UNIT DATE INMATE NAME
STAIE OF MISSOURI DEPARTMENT OF CORRECTIONS NAME OF INSTITUTION ~ PROTECTIVE CUSTODY NEEDS ASSESSMENT/\l\fJUVIER REGISTER NUMBER HOUSING UNIT DATE INMATE NAME - I have been interviewed this date to determine my protective custody needs. The following statement which I have checked and initialed clearly indicates my need or lack of need for protective custody. CHECK -I INITIALS STATEMENT I do not feel that I need protective custody. I am not aware of any enemies among the inmate population, and do not believe I am in any danger. Because of enemies in the general population I am requesting protective custody for the present time. See attached Enemy Listing (MO 931-35"11). The circumstances or persons which cau:Sed me to request protective custody are no longer present in this institution. I therefore request to be released from protective custody back to general population. I assume full responsibility for my safety. I request release from protective custody status upon my transfer to l To my knowledge I have no enemies in the population at the above named institution and I will be able to live in its general population. INMATE SIGNATURE REGISTER NUMBER DATE -. STAFF WITNESS SIGNATU RE TITLE DATE STAFF WITNESS SIGNATURE TITLE DATE I HAVE REVIEWED THE ABOVE REQUEST AND IT IS D APPROVED D DENIED Sl~NATURE OF INSTITUTIONALHEAD DATE MO 931 ·3564 (10·90) DISTRIBUTION: WHITE-CLASSIFICATl(JN FILE : CANARY-INMATE STATE OF MISSOURI FACILITY DEPARTMENT OF CORRECTIONS AREA OFFENDER SAFETY RULES - MACHINE/EQWPMENT OFFENDER NAME (PRINT) DOC NUMBER MACHINE/EQUIPMENT I agree that I will not operate any machinery or equipment until I have been fully trained by a qualified instructor on the machine or equipment's use, cleaning, safety features, care maintenance and authorized to use the machine or equipment. -
![The Echo Structure of Death As a Regenerative Force in Clea, the Fourth Book of Lawrence Durrel's [Sic] Alexandria Quartet](https://docslib.b-cdn.net/cover/2156/the-echo-structure-of-death-as-a-regenerative-force-in-clea-the-fourth-book-of-lawrence-durrels-sic-alexandria-quartet-1062156.webp)
The Echo Structure of Death As a Regenerative Force in Clea, the Fourth Book of Lawrence Durrel's [Sic] Alexandria Quartet
University of the Pacific Scholarly Commons University of the Pacific Theses and Dissertations Graduate School 1972 The echo structure of death as a regenerative force in Clea, the fourth book of Lawrence Durrel's [sic] Alexandria quartet Mareta Suydam Tucker University of the Pacific Follow this and additional works at: https://scholarlycommons.pacific.edu/uop_etds Part of the English Language and Literature Commons Recommended Citation Tucker, Mareta Suydam. (1972). The echo structure of death as a regenerative force in Clea, the fourth book of Lawrence Durrel's [sic] Alexandria quartet. University of the Pacific, Thesis. https://scholarlycommons.pacific.edu/uop_etds/1783 This Thesis is brought to you for free and open access by the Graduate School at Scholarly Commons. It has been accepted for inclusion in University of the Pacific Theses and Dissertations by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. THE ECHO STRUCCJ.'URE OF DEATH l.>..S A HEGENERATIVE FOHCE IN CLEA1 '.['HE FOUlH'H BOOK OF LA11R.8NCB DURRE:C. 1 S AT.J~..?.f.~n.2Ir~..:?~ QT}.l~.l~~E:1~ A 'rhesj.s Presented to the Fa.cul t.y of the Depa:rt.me nt. of Engl.:!_ ;;:;'h Un:i. .,;.-ersit.y of the Pacific In Partial Fulfillment of the Requirements for the Degree 111ast.er of Arts by Maret.a ~:uydam 'rucker Hay, 19 '7 2 'J~I-ill ECHO S~(' RUCTURE OF DEA'rH AS A REGENJ:;RATIVE FO.RCB IN fL~A, 'rilE FOURTH One of ·the principal techniques ur>ed i..;y L<-1\>'n ~nce is echo struc·tureo Echo s·tructures of sim:Llar con<-" truc"i::.ton ( eii:her di:cectly stated or implied) suffuse the t e:..~t v_r:L t.h additional meanings and achieve the matic significance and complct.l':-< ness., Echo st~ruc·ture as a novelif:;t.J . -

Go-Lab Releases of the Lab Owner and Cloud Services (Final) –
Go-Lab Global Online Science Labs for Inquiry Learning at School Collaborative Project in European Union’s Seventh Framework Programme Grant Agreement no. 317601 Deliverable D4.7 Releases of the Lab Owner and Cloud Services (Final) – M33 Editors Wissam Halimi (EPFL) Sten Govaerts (EPFL) Date 30th July, 2015 Dissemination Level Public Status Final c 2015, Go-Lab consortium Go-Lab D4.7 Releases of the Lab Owner and Cloud Services Go-Lab 3176012 of 71 Go-Lab D4.7 Releases of the Lab Owner and Cloud Services The Go-Lab Consortium Beneficiary Beneficiary Name Beneficiary Country Number short name 1 University Twente UT The Nether- lands 2 Ellinogermaniki Agogi Scholi EA Greece Panagea Savva AE 3 École Polytechnique Fédérale de EPFL Switzerland Lausanne 4 EUN Partnership AISBL EUN Belgium 5 IMC AG IMC Germany 6 Reseau Menon E.E.I.G. MENON Belgium 7 Universidad Nacional de Edu- UNED Spain cación a Distancia 8 University of Leicester ULEIC United King- dom 9 University of Cyprus UCY Cyprus 10 Universität Duisburg-Essen UDE Germany 11 Centre for Research and Technol- CERTH Greece ogy Hellas 12 Universidad de la Iglesia de Deusto UDEUSTO Spain 13 Fachhochschule Kärnten - CUAS Austria Gemeinnützige Privatstiftung 14 Tartu Ulikool UTE Estonia 15 European Organization for Nuclear CERN Switzerland Research 16 European Space Agency ESA France 17 University of Glamorgan UoG United King- dom 18 Institute of Accelerating Systems IASA Greece and Applications 19 Núcleo Interactivo de Astronomia NUCLIO Portugal Go-Lab 3176013 of 71 Go-Lab D4.7 Releases of the Lab Owner and Cloud Services Contributors Name Institution Wissam Halimi, Sten Govaerts, Christophe Salzmann, EPFL Denis Gillet Pablo Orduña UDEUSTO Danilo Garbi Zutin CUAS Irene Lequerica UNED Eleftheria Tsourlidaki (Internal Reviewer) EA Lars Bollen (Internal Reviewer) UT Legal Notices The information in this document is subject to change without notice. -

EM Series Panel Computer with Embedded Linux OS Software
EM Series Panel Computer With Embedded Linux OS Software Development Manual Seedsware Corporation http://www.seedsware.co.jp/global/ 17A4A5-00018E-2 Introduction This document describes the development process of Linux applications for the EM Series of product, as well as application specifications. This document describes working with the following models: Model Abbreviated model names EMG7-W207A8-0024-107-01 EMG7-7W EMG7-312A8-00DC-107-01 EMG7-12 EM8-W104A7-0005-207 EM(G)8-4 EMG8-W104A7-0005-207 EM8-205A7-0005-207 EM(G)8-5 EMG8-205A7-0005-207 Copyright and Trademarks ◼ Copyright of this manual is owned by Seedsware Corporation. ◼ Reproduction and/or duplication of this product and/or this manual, in any form, in whole or in part, without permission is strictly prohibited. ◼ This product and descriptions in this document are subject to change without prior notice. Thank you for your understanding. ◼ Although all efforts have been made to ensure the accuracy of this product and its descriptions in this document, should you notice any errors, please feel free to contact us. ◼ Seedsware shall not be held liable for any damages or losses, nor be held responsible for any claims by a third party as a result of using this product. Thank you for your understanding. ◼ Microsoft®, Windows® 7, Windows® 8, and Windows® 10 are registered trademarks of Microsoft Corporation in the United States and other countries. ◼ Oracle VM VirtualBox is a registered trademark of Oracle Corporation. ◼ Other company and product names listed herein are also the trademarks or registered trademarks of their respective owners. -

Linux - Friheden Til at Vælge Distribution
Linux - Friheden til at vælge distribution Version 1.0.20041004 - 2020-12-31 Peter Toft Hanne Munkholm Gitte Wange Jacob Sparre Andersen Kristian Vilmann Henrik Grove Peter Makholm Linux - Friheden til at vælge distributionVersion 1.0.20041004 - 2020-12-31 af Peter Toft, Hanne Munkholm, Gitte Wange, Jacob Sparre Andersen, Kristian Vilmann, Henrik Grove og Peter Makholm Ophavsret © 2003-2005 Forfatterne har ophavsret til bogen, men udgiver den under "Åben dokumentlicens (ÅDL) - version 1.0". Indsigt i valg af distribution. Indholdsfortegnelse Forord...................................................................................................................................................... vii 1. Forord.......................................................................................................................................... vii 2. Linux-bøgerne............................................................................................................................. vii 3. Ophavsret................................................................................................................................... viii 4. Typografi.................................................................................................................................... viii 1. Arch Linux.............................................................................................................................................1 1.1. Målgruppe...................................................................................................................................1 -

X Window System Architecture Overview HOWTO
X Window System Architecture Overview HOWTO Daniel Manrique [email protected] Revision History Revision 1.0.1 2001−05−22 Revised by: dm Some grammatical corrections, pointed out by Bill Staehle Revision 1.0 2001−05−20 Revised by: dm Initial LDP release. This document provides an overview of the X Window System's architecture, give a better understanding of its design, which components integrate with X and fit together to provide a working graphical environment and what choices are there regarding such components as window managers, toolkits and widget libraries, and desktop environments. X Window System Architecture Overview HOWTO Table of Contents 1. Preface..............................................................................................................................................................1 2. Introduction.....................................................................................................................................................2 3. The X Window System Architecture: overview...........................................................................................3 4. Window Managers..........................................................................................................................................4 5. Client Applications..........................................................................................................................................5 6. Widget Libraries or toolkits...........................................................................................................................6 -
![Arxiv:2001.04385V2 [Cs.LG] 1 Jul 2020 Tions (Udes), Which Augments Scientific Models with Machine-Learnable Structures for Scientifically-Based Learning](https://docslib.b-cdn.net/cover/7877/arxiv-2001-04385v2-cs-lg-1-jul-2020-tions-udes-which-augments-scienti-c-models-with-machine-learnable-structures-for-scienti-cally-based-learning-2197877.webp)
Arxiv:2001.04385V2 [Cs.LG] 1 Jul 2020 Tions (Udes), Which Augments Scientific Models with Machine-Learnable Structures for Scientifically-Based Learning
Universal Differential Equations for Scientific Machine Learning Christopher Rackauckas1,a,b, Yingbo Mac, Julius Martensend, Collin Warnera, Kirill Zubove, Rohit Supekara, Dominic Skinnera, Ali Ramadhana, and Alan Edelmana aMassachusetts Institute of Technology bUniversity of Maryland, Baltimore cJulia Computing dUniversity of Bremen eSaint Petersburg University July 2, 2020 Abstract In the context of science, the well-known adage “a picture is worth a thousand words” might well be “a model is worth a thousand datasets.” Scientific models, such as Newtonian physics or biological gene regula- tory networks, are human-driven simplifications of complex phenomena that serve as surrogates for the countless experiments that validated the models. Recently, machine learning has been able to overcome the in- accuracies of approximate modeling by directly learning the entire set of nonlinear interactions from data. However, without any predetermined structure from the scientific basis behind the problem, machine learning approaches are flexible but data-expensive, requiring large databases of homogeneous labeled training data. A central challenge is reconciling data that is at odds with simplified models without requiring “big data”. In this work we develop a new methodology, universal differential equa- arXiv:2001.04385v2 [cs.LG] 1 Jul 2020 tions (UDEs), which augments scientific models with machine-learnable structures for scientifically-based learning. We show how UDEs can be utilized to discover previously unknown governing equations, accurately extrapolate beyond the original data, and accelerate model simulation, all in a time and data-efficient manner. This advance is coupled with open-source software that allows for training UDEs which incorporate physical constraints, delayed interactions, implicitly-defined events, and intrinsic stochasticity in the model. -
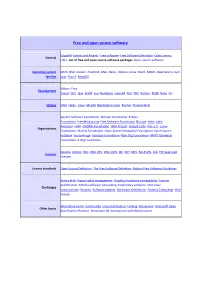
Free and Open Source Software
Free and open source software Copyleft ·Events and Awards ·Free software ·Free Software Definition ·Gratis versus General Libre ·List of free and open source software packages ·Open-source software Operating system AROS ·BSD ·Darwin ·FreeDOS ·GNU ·Haiku ·Inferno ·Linux ·Mach ·MINIX ·OpenSolaris ·Sym families bian ·Plan 9 ·ReactOS Eclipse ·Free Development Pascal ·GCC ·Java ·LLVM ·Lua ·NetBeans ·Open64 ·Perl ·PHP ·Python ·ROSE ·Ruby ·Tcl History GNU ·Haiku ·Linux ·Mozilla (Application Suite ·Firefox ·Thunderbird ) Apache Software Foundation ·Blender Foundation ·Eclipse Foundation ·freedesktop.org ·Free Software Foundation (Europe ·India ·Latin America ) ·FSMI ·GNOME Foundation ·GNU Project ·Google Code ·KDE e.V. ·Linux Organizations Foundation ·Mozilla Foundation ·Open Source Geospatial Foundation ·Open Source Initiative ·SourceForge ·Symbian Foundation ·Xiph.Org Foundation ·XMPP Standards Foundation ·X.Org Foundation Apache ·Artistic ·BSD ·GNU GPL ·GNU LGPL ·ISC ·MIT ·MPL ·Ms-PL/RL ·zlib ·FSF approved Licences licenses License standards Open Source Definition ·The Free Software Definition ·Debian Free Software Guidelines Binary blob ·Digital rights management ·Graphics hardware compatibility ·License proliferation ·Mozilla software rebranding ·Proprietary software ·SCO-Linux Challenges controversies ·Security ·Software patents ·Hardware restrictions ·Trusted Computing ·Viral license Alternative terms ·Community ·Linux distribution ·Forking ·Movement ·Microsoft Open Other topics Specification Promise ·Revolution OS ·Comparison with closed -

SUSE LINUX Enterprise Server
SUSE LINUX Enterprise Server INSTALLATION AND ADMINISTRATION 9. Edition 2004 Copyright © This publication is intellectual property of SUSE LINUX AG. Its contents can be duplicated, either in part or in whole, provided that a copyright label is visibly located on each copy. All information found in this book has been compiled with utmost attention to de- tail. However, this does not guarantee complete accuracy. Neither SUSE LINUX AG, the authors, nor the translators shall be held liable for possible errors or the consequences thereof. Many of the software and hardware descriptions cited in this book are registered trademarks. All trade names are subject to copyright restrictions and may be reg- istered trade marks. SUSE LINUX AG essentially adheres to the manufacturer’s spelling. Names of products and trademarks appearing in this book (with or with- out specific notation) are likewise subject to trademark and trade protection laws and may thus fall under copyright restrictions. Please direct suggestions and comments to [email protected]. Authors: Stefan Behlert, Frank Bodammer, Stefan Dirsch, Olaf Donjak, Roman Drahtmüller, Torsten Duwe, Thorsten Dubiel, Thomas Fehr, Stefan Fent, Werner Fink, Kurt Garloff, Carsten Groß, Joachim Gleißner, Andreas Grünbacher, Franz Hassels, Andreas Jaeger, Klaus Kämpf, Hubert Mantel, Lars Marowsky-Bree, Johannes Meixner, Lars Müller, Matthias Nagorni, Anas Nashif, Siegfried Olschner, Peter Pöml, Thomas Renninger, Heiko Rommel, Marcus Schäfer, Nicolaus Schüler, Klaus Singvogel, Hendrik Vogelsang, Klaus G. Wagner, Rebecca Walter, Christian Zoz Translators: Olaf Niepolt, Daniel Pisano Editors: Jörg Arndt, Antje Faber, Berthold Gunreben, Roland Haidl, Jana Jaeger, Edith Parzefall, Ines Pozo, Thomas Rölz, Thomas Schraitle, Rebecca Walter Layout: Manuela Piotrowski, Thomas Schraitle Setting: DocBook-XML und LATEX This book has been printed on 100 % chlorine-free bleached paper. -

Curso De Introducción Al Sistema Operativo Gnu/Linux
CURSO DE INTRODUCCIÓN AL SISTEMA OPERATIVO GNU/LINUX Guía del alumno Febrero de 2004 ls Autores: José Enrique García Ramos Francisco Pérez Bernal José Rodríguez Quintero Fuentes: “Sistema operativo GNU/Linux básico”, R. Baig Viñas y F. Auli Linàs, UOC (Barcelona, 2003). Scientific Computing with Free GNU/Linux Software HOWTO que puede encontrarse en ftp://ibiblio.org/pub/Linux/docs/HOWTO. http://www.ecn.wfu.edu/ cottrell/wp.html publicado por Allin Cot- trell y traducido por José María Martín Olalla. “Curso práctico de Linux”, Claus Denk, (Sevilla, 1995 y 1999). Puede encontrarse en http:/www.numerix.es “debian-reference”, que puede encontrarse en http://www.debian.org/doc/- manuals/debian-reference. HOWTO’s en inglés. Versión 1.0. Copyright °c 2004 J.E. García Ramos, F. Pérez Bernal, J. Rodríguez Quintero. Este manual es software libre, puede ser redistribuido y/o modificado bajo los términos de la licencia GNU General Public License publicada por la Free Software Foundation. Este texto se distribuye con la esperanza de que sea útil, pero no existe ninguna garantía sobre él. Curso GNU/Linux III Lecciones del curso de “Introducción al Sistema Operativo GNU/Linux” Lección 1 Presentación: Software libre, GNU y GNU/Linux. Lección 2 Instalación de Debian GNU/Linux. Knoppix. Lección 3 Comandos básicos de Unix/Linux. Lección 4 Tareas básicas de configuración: red, modem, impresora, etc. Lección 5 El sistema X-Window: window managers, Gnome, KDE y mucho más. Lección 6 Editores de texto: emacs, vi, nano, abiword y latex. Lección 7 Más allá de Microsoft Office: OpenOffice y Staroffice. Lección 8 Conexión a la red (ssh, telnet, ftp, etc) y navegadores (mozilla, netscape, lynx, opera, konqueror, etc.) Lección 9 Tratamiento de gráficos. -

World Bank Document
Public Disclosure Authorized By Paul Dravis Public Disclosure Authorized Open Source Software Public Disclosure Authorized Perspectives for Development Public Disclosure Authorized Table of Contents Preface 2 Executive Summary 4 Introduction 5 Review Committee Members 6 Acknowledgements Part I: Global Perspectives on Open Source Software Use 7 Global Interest is Growing 7 Australia, Brazil, China/Japan/South Korea Collaboration 7 We wish to thank the following Denmark, European Commission, Germany, India, Malaysia 8 individuals for their assistance Philippines, Pakistan, Thailand, Spain 9 and insights provided during South Africa, Sweden, United Kingdom, United States 10 this project: Part II: Case Studies in Developing Countries 12 Larry Augustin, Nick Arnett, Using OSS in Developing Countries 12 Sao Paulo, Brazil — The Telecenter Project 13 Peter Antonio B. Banzon, Tajikistan — Introducing Localized ICT 14 Rosalie Blake, Belén Caballero Goa (India) Schools Computer Project 16 Muñoz, Jordi Carrasco-Muñoz, Laos — The Jhai Remote Village IT System 17 Carlos Castro, Bart Decrem, Pablo A. Destefanis, Derek Part III: The Current Dynamics of Open Source Software 20 Dresser, Pat Eyler, Lee Benefits Vary Based on Use and Focus 20 Felsenstein, Isidro Fernandez, Local ICT Capacity Development 21 Marco Figueiredo, Miguel de OSS is Not an “All or Nothing” Proposition 27 Icaza, Jorg Janke, Joris Komen, Open Source 101: What is it all about? 23 David Land, Daryl Martyris, From the Low to the High End of Computing 26 Scott McNeil, Jim McQuillan, The -

A Survey of the Use of Crowdsourcing in Software Engineering
A Survey of the Use of Crowdsourcing in Software Engineering Ke Mao⇤, Licia Capra, Mark Harman, Yue Jia Department of Computer Science, University College London, Malet Place, London, WC1E 6BT, UK Abstract The term ‘crowdsourcing’ was initially introduced in 2006 to describe an emerging distributed problem-solving model by online workers. Since then it has been widely studied and practiced to support software engineering. In this paper we provide a compre- hensive survey of the use of crowdsourcing in software engineering, seeking to cover all literature on this topic. We first review the definitions of crowdsourcing and derive our definition of Crowdsourcing Software Engineering together with its taxonomy. Then we summarise industrial crowdsourcing practice in software engineering and corresponding case studies. We further analyse the software engineering domains, tasks and applications for crowdsourcing and the platforms and stakeholders involved in realising Crowdsourced Software Engineering solutions. We conclude by exposing trends, open issues and opportunities for future research on Crowdsourced Software Engineering. Keywords: Crowdsourced software engineering, software crowdsourcing, crowdsourcing, literature survey 1. Introduction crowdsourcing in software engineering, yet many authors claim that there is ‘little work’ on crowdsourcing for/in software en- Crowdsourcing is an emerging distributed problem-solving gineering (Schiller and Ernst, 2012; Schiller, 2014; Zogaj et al., model based on the combination of human and machine compu- 2014). These authors can easily be forgiven for this miscon- 30 tation. The term ‘crowdsourcing’ was jointly1 coined by Howe ception, since the field is growing quickly and touches many 5 and Robinson in 2006 (Howe, 2006b). According to the widely disparate aspects of software engineering, forming a literature accepted definition presented in the article, crowdsourcing is that spreads over many di↵erent software engineering applica- the act of an organisation outsourcing their work to an unde- tion areas.