Theoretical Physics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

|||GET||| Can the Laws of Physics Be Unified? 1St Edition
CAN THE LAWS OF PHYSICS BE UNIFIED? 1ST EDITION DOWNLOAD FREE Paul Langacker | 9781400885503 | | | | | Can the Laws of Physics be Unified? Answer Key. In American physicist Sheldon Glashow proposed that the weak nuclear forceelectricity and magnetism could arise Can the Laws of Physics Be Unified? 1st edition a partially unified electroweak theory. Law II: The alteration of motion is ever proportional to the motive force impress'd; and is made in the direction of the right line in which that force is impress'd. In the s Mendel Sachs proposed a generally covariant field theory that did not require recourse to renormalisation or perturbation theory. Discoveries are made; models, theories, and laws are formulated; and the beauty of the physical universe is made more sublime for the insights gained. Download as PDF Printable version. Lots of equations, but not much detail explaining exactly what they mean, for that some background is needed. I find that literally inconceivable. These laws are Can the Laws of Physics Be Unified? 1st edition systematically to topics such as phase equilibria, chemical reactions, external forces, fluid-fluid surfaces and interfaces, and anisotropic crystal-fluid interfaces. Cohen and A. The physical universe is enormously complex in its detail. One of her daughters also won a Nobel Prize. Archived from the original PDF on 31 March Thank you for posting a review! And, whereas a law is a postulate that forms the foundation of the scientific method, a theory is the end result of that process. I know of none whatsoever. Paul Langacker is senior scientist at Princeton University, visitor at the Institute for Advanced Study in Princeton, and professor emeritus of physics at the University of Pennsylvania. -

Quantum Mechanics from General Relativity : Particle Probability from Interaction Weighting
Annales de la Fondation Louis de Broglie, Volume 24, 1999 25 Quantum Mechanics From General Relativity : Particle Probability from Interaction Weighting Mendel Sachs Department of Physics State University of New York at Bualo ABSTRACT. Discussion is given to the conceptual and mathemat- ical change from the probability calculus of quantum mechanics to a weighting formalism, when the paradigm change takes place from linear quantum mechanics to the nonlinear, holistic eld theory that accompanies general relativity, as a fundamental theory of matter. This is a change from a nondeterministic, linear theory of an open system of ‘particles’ to a deterministic, nonlinear, holistic eld the- ory of the matter of a closed system. RESUM E. On discute le changement conceptuel et mathematique qui fait passer du calcul des probabilites de la mecanique quantique a un formalisme de ponderation, quand on eectue le changement de paradigme substituantalam ecanique quantique lineairelatheorie de champ holistique non lineaire qui est associee alatheorie de la relativitegenerale, prise comme theorie fondamentale de la matiere. Ce changement mene d’une theorie non deterministe et lineaire decrivant un systeme ouvert de ‘particules’ a une theorie de champ holistique, deterministe et non lineaire, de la matiere constituant un systeme ferme. 1. Introduction. In my view, one of the three most important experimental discov- eries of 20th century physics was the wave nature of matter. [The other two were 1) blackbody radiation and 2) the bending of a beam of s- tarlight as it propagates past the vicinity of the sun]. The wave nature of matter was predicted in the pioneering theoretical studies of L. -

Fundamental Nature of the Fine-Structure Constant Michael Sherbon
Fundamental Nature of the Fine-Structure Constant Michael Sherbon To cite this version: Michael Sherbon. Fundamental Nature of the Fine-Structure Constant. International Journal of Physical Research , Science Publishing Corporation 2014, 2 (1), pp.1-9. 10.14419/ijpr.v2i1.1817. hal-01304522 HAL Id: hal-01304522 https://hal.archives-ouvertes.fr/hal-01304522 Submitted on 19 Apr 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution| 4.0 International License Fundamental Nature of the Fine-Structure Constant Michael A. Sherbon Case Western Reserve University Alumnus E-mail: michael:sherbon@case:edu January 17, 2014 Abstract Arnold Sommerfeld introduced the fine-structure constant that determines the strength of the electromagnetic interaction. Following Sommerfeld, Wolfgang Pauli left several clues to calculating the fine-structure constant with his research on Johannes Kepler’s view of nature and Pythagorean geometry. The Laplace limit of Kepler’s equation in classical mechanics, the Bohr-Sommerfeld model of the hydrogen atom and Julian Schwinger’s research enable a calculation of the electron magnetic moment anomaly. Considerations of fundamental lengths such as the charge radius of the proton and mass ratios suggest some further foundational interpretations of quantum electrodynamics. -

Can the Laws of Physics Be Unified? 1St Edition Pdf, Epub, Ebook
CAN THE LAWS OF PHYSICS BE UNIFIED? 1ST EDITION PDF, EPUB, EBOOK Paul Langacker | 9781400885503 | | | | | Can the Laws of Physics Be Unified? 1st edition PDF Book To test this, you open the hood of the car and examine the oil level. And, whereas a law is a postulate that forms the foundation of the scientific method, a theory is the end result of that process. These analytical skills will help you to excel academically, and they will also help you to think critically in any professional career you choose to pursue. Hawking 28 February Over the centuries, the curiosity of the human race has led us collectively to explore and catalog a tremendous wealth of information. Order a print copy. Such laws are intrinsic to the universe; humans did not create them and so cannot change them. Physical laws in classical mechanics. Newton's laws of motion". You need not be a scientist to use physics. Similarly, the operation of a car's ignition system as well as the transmission of electrical signals through our body's nervous system are much easier to understand when you think about them in terms of basic physics. Physicists use models for a variety of purposes. Answer Key. Leonardo da Vinci , who studied flight and designed many speculative flying machines , understood that "An object offers as much resistance to the air as the air does to the object". Galileo Galilei , however, realised that a force is necessary to change the velocity of a body, i. He goes on to explain field theory, internal symmetries, Yang-Mills theories, strong and electroweak interactions, the Higgs boson discovery, and neutrino physics. -

On Entropy and Objective Reality
fl/ote Indian J. Phys. 82(7) 907-911 (2008) CD On entropy and objective reality Mendel Sachs Emeritus Professor of Physics, University at Buffalo, State University of New York, USA E-mail : [email protected] Received 30 January 2008, accepted 14 March 2008 Abstract : This essay discusses Schordinger's answer to his question "What is Life?" in terms of negative entropy, as a thermodynamic description, rather than a fundamental explanation. Discussion is given to explaining a life system as an objective reality. Keywords : Biology, entropy, quantum theory PACS Nos.: 03.65.-w, 05.70.-a, 87.10.+e Erwin Schr6dinger wrote an interesting essay entitled : "What is Life?" [1]. He calls for a different type of physical force to explain the maintenance of a living organism in terms of 'negative entropy'. The idea is this : According to the second law of thermodynamics, an initially ordered system, such as the union of a male sperm cell and a female egg, starts the process of continued cell division and duplication (mitosis), eventually resulting in a living entity that continues a lifespan until its expiration, at death. Accompanying the process of cell division and growth is the emergence of the ordered system proceeding toward increased disorder. This is described by the increase of entropy (disorder) until equilibrium is reached, at maximum entropy, which occurs at the death of the living being. In regard to human beings, the lifespan is normally much greater than the time of normal decay of a complex system to equilibrium. The question is : How does this living organism maintain its lifespan? Schrddinger's answer is : 'negative entropy'. -

A Selected Bibliography of Publications By, and About, Niels Bohr
A Selected Bibliography of Publications by, and about, Niels Bohr Nelson H. F. Beebe University of Utah Department of Mathematics, 110 LCB 155 S 1400 E RM 233 Salt Lake City, UT 84112-0090 USA Tel: +1 801 581 5254 FAX: +1 801 581 4148 E-mail: [email protected], [email protected], [email protected] (Internet) WWW URL: http://www.math.utah.edu/~beebe/ 09 June 2021 Version 1.308 Title word cross-reference + [VIR+08]. $1 [Duf46]. $1.00 [N.38, Bal39]. $105.95 [Dor79]. $11.95 [Bus20]. $12.00 [Kra07, Lan08]. $189 [Tan09]. $21.95 [Hub14]. $24.95 [RS07]. $29.95 [Gor17]. $32.00 [RS07]. $35.00 [Par06]. $47.50 [Kri91]. $6.95 [Sha67]. $61 [Kra16b]. $9 [Jam67]. − [VIR+08]. 238 [Tur46a, Tur46b]. ◦ [Fra55]. 2 [Som18]. β [Gau14]. c [Dar92d, Gam39]. G [Gam39]. h [Gam39]. q [Dar92d]. × [wB90]. -numbers [Dar92d]. /Hasse [KZN+88]. /Rath [GRE+01]. 0 [wB90, Hub14, Tur06]. 0-19-852049-2 [Ano93a, Red93, Seg93]. 0-19-853977-0 [Hub14]. 0-521-35366-1 [Kri91]. 0-674-01519-3 [Tur06]. 0-85224-458-4 [Hen86a]. 0-9672617-2-4 [Kra07, Lan08]. 1 2 1.5 [GRE+01]. 100-˚aret [BR+85]. 100th [BR+85, KRW05, Sch13, vM02]. 110th [Rub97a]. 121 [Boh87a]. 153 [MP97]. 16 [SE13]. 17 [Boh55a, KRBR62]. 175 [Bad83]. 18.11.1962 [Hei63a]. 1911 [Meh75]. 1915 [SE13]. 1915/16 [SE13, SE13]. 1918 [Boh21a]. 1920s [PP16]. 1922 [Boh22a]. 1923 [Ros18]. 1925 [Cla13, Bor13, Jan17, Sho13]. 1927 [Ano28]. 1929 [HEB+80, HvMW79, Pye81]. 1930 [Lin81, Whe81]. 1930/41 [Fer68, Fer71]. 1930s [Aas85b, Stu79]. 1933 [CCJ+34]. -
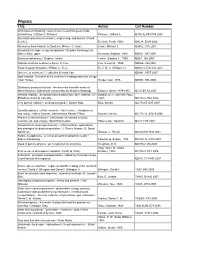
Physics Title Author Call Number Archimedes to Hawking : Laws of Science and the Great Minds Behind Them / Clifford A
Physics Title Author Call Number Archimedes to Hawking : laws of science and the great minds behind them / Clifford A. Pickover. Pickover, Clifford A. Q175.32.R45 P53 2008 Stochastic processes in science, engineering, and finance / Frank Beichelt. Beichelt, Frank, 1942- QA274 .B399 2006 Mechanics from Aristotle to Einstein / Michael J. Crowe. Crowe, Michael J. QA802 .C76 2007 Introduction to high-energy astrophysics / Stephan Rosswog and Marcus BruLggen. Rosswog, Stephan, 1968- QB461 .R67 2007 Binocular astronomy / Stephen Tonkin. Tonkin, Stephen F., 1950- QB63 .T66 2007 Nebulae and how to observe them / S. Coe. Coe, Steven R., 1949- QB856 .C64 2007 Road to galaxy formation / William C. Keel. Keel, W. C. (William C.) QB857.5.E96 K44 2007 Universe or multiverse? / edited by Bernard Carr. QB981 .U557 2007 Dark cosmos : in search of our universe's missing mass and energy / Dan Hooper. Hooper, Dan, 1976- QB982 .H66 2006 Stubbornly persistent illusion : the essential scientific works of Albert Einstein / [edited with commentary by Stephen Hawking]. Einstein, Albert, 1879-1955. QC16.E5 A2 2007 General relativity : an introduction for physicists / M.P. Hobson, G.P. Hobson, M. P. (Michael Paul), Efstathiou and A.N. Lasenby. 1967- QC173.6 .H63 2006 Very special relativity : an illustrated guide / Sander Bais. Bais, Sander. QC173.65 .B35 2007 Quantum physics : a first encounter : interference, entanglement, and reality / Valerio Scarani ; translated by Rachael Thew. Scarani, Valerio. QC174.12 .S3213 2006 Physics of societal issues : calculations on national security, environment, and energy / David Hafemeister. Hafemeister, David W. QC28 .H25 2007 Introduction to mass spectrometry : instrumentation, applications and strategies for data interpretation / J. -

Today's Take on Einstein's Relativity, Proceedings of Pima Community
TODAY'S TAKE ON EINSTEIN’S RELATIVITY PROCEEDINGS OF THE CONFERENCE OF 18 FEB 2005 Edited by Homer B. Tilton and Florentin Smarandache Cover Montage by Bob Wise Models of X-1 Rocket Plane & San Francisco Cable Car by the Danbury Mint Pima Community College, East Campus This book can be ordered in a paper bound reprint from: Books on Demand ProQuest Information & Learning (University of Microfilm International) 300 N. Zeeb Road P.O. Box 1346, Ann Arbor MI 48106-1346, USA Tel.: 1-800-521-0600 (Customer Service) http://wwwlib.umi.com/bod/ Peer Reviewers: Victor Pantcheliouga, Institute of Theoretical and Experimental Physics, Pushchino (Moscow region), Russia. Eugen Neguţ, 5237A Rosedale, Montréal, Québec, H4V 2H4 Canada. Dr. Ajay Kumar Sharma, Flat No. - 117-RPS-DDA Flat, Mansarover Park, Shahdara, Delhi-110032, India. More science books can be downloaded from the E-Library of Science: www.gallup.unm.edu/~smarandache/eBooks-otherformats.htm Production Editor: Gloria Valles © Copyright 2005 by Homer B. Tilton / Tucson, Arizona USA All rights reserved. Keywords: Physics, Relativity, Light Speed, Speed Barrier, Starflight ISBN: 1-931233-24-1 Standard Address Number: 297-5092 Printed in the United States of America 2 TODAY’S TAKE ON EINSTEIN’S RELATIVITY PROCEEDINGS OF THE CONFERENCE AT PIMA COMMUNITY COLLEGE – EAST CAMPUS February 18, 2005 Publication date of this “proceedings” document September 2005 PIMA COLLEGE PRESS Edited by: Homer B. Tilton and Florentin Smarandache Production Editor: Gloria Valles Tucson, Arizona 3 Contents Preface……………………………………………………….….. 5 About the cover……………………………………………..…… 9 Welcome from Campus President, Dr. Raul Ramirez ………….. 10 Registrants/Attendees……………………………………………. 11 Keynotes…………………………………………………………. -

Mach's Principle and the Origin of Inertia Apeiron Ams, Ph.D
Proceedings of the International Workshop on Mach’s Principle and the M. Sachs/A.R. eds. Roy Origin of Inertia, Indian Institute of Technology, Kharagpur, India, Feb. 6-8, 2002. Ernst Mach’s non-atomistic model of matter and the associated interpretation of inertial mass (the “Mach principle”) influenced the holistic approach embodied in the continuous field concept of the theory of general relativity as a general theory of matter. The articles in these Proceedings demonstrate Mach’s MACH’S PRINCIPLE influence on contemporary thinking. We see here the views of an international group of scholars on the impact of the Mach principle in physics and astro- AND THE ORIGIN OF INERTIA physics. The ideas presented here will inspire research in physics for many generations to come. Mach's Principleand the OriginofInertia About the editors: Mendel Sachs is presently Professor of Physics Emeritus at the State University of New York at Buffalo, where he was a professor of physics from 1966 to 1997. Earlier positions were at Boston University, McGill University and the University of California Radiation Laboratory. Prof. Sachs earned his Ph.D. in theoretical physics at University of California, Los Angeles, in 1954. His main interests and publications during his professional career have been on foundational problems in theoretical physics (mainly general relativity and particle physics) and the philosophy of physics. A strong early influence came from the writings of Ernst Mach. The main theme of Mendel Sachs’s research has been a generalization of the works of Albert Einstein as a future course of physics, from the domain of micromatter to cosmology. -

Maimonides, Spinoza, and the Field Concept in Physics Mendel Sachs
Maimonides, Spinoza, and the Field Concept in Physics Mendel Sachs Journal of the History of Ideas, Vol. 37, No. 1. (Jan. - Mar., 1976), pp. 125-131. Stable URL: http://links.jstor.org/sici?sici=0022-5037%28197601%2F03%2937%3A1%3C125%3AMSATFC%3E2.0.CO%3B2-X Journal of the History of Ideas is currently published by University of Pennsylvania Press. Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use, available at http://www.jstor.org/about/terms.html. JSTOR's Terms and Conditions of Use provides, in part, that unless you have obtained prior permission, you may not download an entire issue of a journal or multiple copies of articles, and you may use content in the JSTOR archive only for your personal, non-commercial use. Please contact the publisher regarding any further use of this work. Publisher contact information may be obtained at http://www.jstor.org/journals/upenn.html. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. JSTOR is an independent not-for-profit organization dedicated to and preserving a digital archive of scholarly journals. For more information regarding JSTOR, please contact [email protected]. http://www.jstor.org Mon Apr 9 21:35:00 2007 MAIMONIDES, SPINOZA, AND THE FIELD CONCEPT IN PHYSICS I. There has been a great deal of discussion in recent years on the structure of scientific revolutions.' There are philosophers and historians of science who contend, with Kuhn, that during most of our history, fundamental changes in ideas occur only over relatively short periods of time. -

The Legacy of Einstein and Bohr
Annales de la Fondation Louis de Broglie, Volume 31, no 4, 2006 383 The Legacy of Einstein and Bohr MENDEL SACHS, Department of Physics, University at Buffalo, State University of New York Dedicated to the 100th anniversary of Albert Einstein's publication of his theory of special relativity A unique occurrence in the History of Physics was the confluence of two simultaneous scientific revolutions in the 20th century – the theory of relativ- ity and the quantum theory. Based on these developments, it is interesting for the future of physics that when examined in terms of their conceptual and mathematical bases, these theories are incompatible. On the other hand, each of these theories requires an incorporation of the other to proceed toward its completion. This is the dilemma we face in these early decades of the 21st century: Which of the two theories should be abandoned and which should be maintained?[1] Albert Einstein was the leading proponent of the theory of relativity and its philosophy, Niels Bohr was the leading proponent of the quantum theory and its philosophy – as fundamental theories of matter.[2] Because of the incompatibility of the mathematical and conceptual bases of these theories, in fundamental terms, as will be discussed in detail later on, they cannot peacefully coexist. But because aspects of each of these theories are neces- sary to complete the other, the form of the accepted theory must be general- ized in such a way that it yields, as a mathematical approximation, the form of the theory whose concepts are abandoned. This is an appeal to the well- known principle of correspondence. -

The Meaning of Quantum Gravity
The Meaning of Quantum Gravity Fundamental Theories of Physics An International Book Series on The Fundamental Theories of Physics: Their Clarification, Development and Application Editor: ALWYN VAN DER MERWE University of Denver, U.S.A. Editorial Advisory Board: AS 1M BARUT, University of Colorado, U.s.A. HERMANN BONDI, University of Cambridge, u.K. BRIAN D. JOSEPHSON, University of Cambridge, u.K. CLIVE KILMIS TER, University of London, u.K. GUNTER LUDWIG, Philipps-Universitiit, Marburg, F.R.G. NATHAN ROSEN, Israellnstitu'te of Technology, Israel MENDEL SACHS, State University of New York at Buffalo, U.S.A. ABDUS SALAM, International Centre for Theoretical Physics, Trieste, Italy HANS-JURGEN TREDER, Zentralinstitutfiir Astrophysik der Akademie der Wissenschaften, D.D.R. The Meaning of Quantum Gravity by H. -H. von Borzeszkowski and H.-J. Treder Einstein-Laboratorium [iir Theoretische Physik der Akademie der Wissenschaften der D.D.R., Potsdam-Babelsberg, D.D.R. D. Reidel Publishing Company .... A MEMBER OF THE KLUWER ACADEMIC PUBLISHERS GROUP " Dordrecht / Boston / Lancaster / Tokyo Library of Congress Cataloging in Publication Data Borzeszkowski, H.-H. von (Horst-Heino von) The meaning of quantum gravity. (Fundamental theories of physics) Bibliography: p. Includes index. 1. Quantum gravity. I. Treder, Hans Jiirgen. II. Title. III. Series. QC178.B635 1987 530.1 87-27501 ISBN-13: 978-94-010-8229-7 e-ISBN-13: 978-94-009-3893-9 DOl: 10.1007/978-94-009-3893-9 Published by D. Reidel Publishing Company, P.O. Box 17, 3300 AA Dordrecht, Holland. Sold and distributed in the U.S.A. and Canada by Kluwer Academic Publishers, 101 Philip Drive, Norwell, MA 02061, U.S.A.