DOCSLIB.ORG

Coordinate Systems CS 1 Concepts of Primary Interest: the Line Element

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Coordinate Systems CS 1 Concepts of Primary Interest: the Line Element Coordinate Systems Concepts of primary interest: The line element Coordinate directions Area and volume elements Sample calculations: Coordinate direction derivatives Velocity and acceleration in polar coordinates Application examples: Velocity and acceleration in spherical coordinates **** add solid angle Tools of the Trade Changing a vector Area Elements: dA = dr12 dr *** TO Add ***** Appendix I – The Gradient and Line Integrals Coordinate systems are used to describe positions of particles or points at which quantities are to be defined or measured. They are often used as references for specifying directions. The coordinate system or reference frame is used extensively in describing the physical problem or situation, but it is not a part of the problem. No physical result can depend on the choice of coordinates. The coordinate system is a passive aid to the observer, and it may be chosen or adjusted to suit the purposes of the observer. Problem statements may use a coordinate system as a convenience, but no physical problem comes with axes glued to it. We add them to facilitate the description of the problem. Once the coordinates have been chosen for a problem and the description has been started, further changes are usually not advised as a complicated transformation scheme is often required to translate information stated relative to one set of coordinates into a form suitable for use in another set of coordinates. A system of coordinates for three dimensions assigns an ordered triplet of numbers [(x, y, z) or (q1,q2,q3)] to each point in space. Three such coordinate systems are commonly used by undergraduate physics majors: Cartesian, cylindrical and spherical. A common characteristic of these systems is that they are locally orthonormal coordinate systems. This phrase means that each coordinate system specifies three mutually CS 1 Coordinate Systems perpendicular (orthogonal and unity normalized) directions at every point in space. An infinitesimal displacement along one coordinate direction is independent of small displacements along the other coordinate directions because their directions are mutually perpendicular. For example, in Cartesian coordinates, a displacement in the x direction does not change the y or z coordinate. Each system is to be discussed in a parallel fashion to emphasize their common features and their distinguishing characteristics. Rene Descartes (1596-1650): French scientific philosopher who developed a theory known as the mechanical philosophy. This philosophy was highly influential until superseded by Newton’s methodology. Descartes was the first to make a graph, allowing a geometric interpretation of a mathematical function and giving his name to Cartesian coordinates. Eric W. Weisstein @ scienceworld.wolfram.com/biography/Descartes.html Cartesian Coordinates To understand a coordinate system, you must know its relation to the Cartesian coordinate system, the representation of the position vector, the shapes of the constant coordinate surfaces, the three independent coordinate directions, and the line element represented as d or dr . For this reason, the Cartesian system is studied first. The relations between the coordinates of a Cartesian system and those of a second Cartesian system with the same origin and axes directions are: x' = x, y' = y, and z' = z. (A more interesting set of transformations is used to relate one set of Cartesian coordinates to another Cartesian set with a different origin or orientation. That problem is studied in a second semester course in mechanics.) Constant Coordinate Surfaces: The constant coordinate surfaces are planes parallel to the plane defined by the other two axes. For example, x = a is a plane parallel to the y-z plane that is perpendicular to the x axis at the point (a, 0, 0). The point (a, b, c) is located at the intersection of the planes x = a, y = b, and z =c. You should sketch some constant coordinate planes illustrating the intersections of pairs and triplets of such planes. Coordinate Orbits: We define a coordinate orbit as the locus of points mapped as one coordinate runs through its full range in the positive sense while the other coordinates are held fixed. An x-orbit is an infinite line parallel to the x-axis that passes through the x = 0 plane at (0, y, z). Position Vector: The position vector for a point P is the displacement from the origin to that point. The CS 2 Coordinate Systems ˆˆˆ Cartesian position vector corresponding to the point P = (xP, yP, zP) is rxiyjzkPP P P. Coordinate Directions: One can find the coordinate directions by examining the change in position due to a small positive variation in one coordinate while the other coordinates are kept fixed. Imagine the Cartesian coordinate axes and a point (x, y, z) hanging in otherwise empty space. Increase each coordinate in turn by a small positive increment to visualize each of the independent coordinate directions { xˆˆ,,yzˆ }(also known as:{ ˆˆˆ ijk,, }; { eeeˆˆˆx ,,yz} or { eeeˆˆˆ123,,}). The xˆ direction is the direction a point is displaced if its x coordinate is given a small positive increment while its y and z coordinates are held fixed. x dxiˆˆ yj zkˆˆ xi ˆˆ yj zk rx(,,)(,,) dxyz rxyz xˆ Limit iˆ dx0 rx(,,)(,,) dxyz rxyz dx FORGET the equation! It is the picture that you need. Imagine the axes and point hanging out in space. In your mind, move the point from (x, y, z) to (x + x, y, z). In what direction did the point move? Line Element: The next vital quantity is the line element which is found as the displacement from the point (x, y, z) to the point (x + dx, y + dy, z + dz) at which each of the coordinates has been given an infinitesimal increment. d dr rx(, dxydyz ,)(,,) dz rxyz dxiˆˆ dyj dzkˆ Area and volume elements are built up from the mutually orthogonal components of the line element. For an area element with its normal in the x direction, x is fixed, and dAx = dy dz. The area element is just the product of the two perpendicular components of the line element. All three components of the differential of area are summarized as: ˆˆˆˆ ˆ ˆ dA dAxy i dA j dA z k dy dzi dz dx j dx dy k (There are other notations for dA such as dS, and dr2 .) Note that the direction of an area element is defined to be one of its normal directions. For a closed surface, the convention is to choose the outward directed normal. For the area element dA , the convention is that one takes the cross product of the each pair of the dir4ected components of the line element in right hand rule order. dAdxiˆˆ dy j dy ˆj dz kˆˆ dz k dxi ˆ dy dziˆˆ dz dx j dxdy kˆ Finally, we get the volume element by computing the product of the three orthogonal components of the line element. A volume element can be swept out by taking a small area element and moving it a small distance in the direction of its normal, or it can be computed as the triple vector product of the line elements component CS 3 Coordinate Systems vectors. ˆˆ ˆ ˆ ˆˆ dV dxi dAxy i dy j dA j dz k dA z k dx dy dz dV dxiˆˆ() dy j dz kˆ dV = dx dy dz z ˆ kˆ dz k dyˆ j dA = dy dz x dz kˆ ˆj iˆ ˆ dyˆ j dyˆ j dxi ˆ y dxi dV = dx dy dz x dAz = dx dy Everything is constructed from the components of the line element. Note the coordinate cube (volume element) has a small coordinate corner at (x,y,z) and a large coordinate corner at (x + dx, y + dy, z + dz). The components of the line element {,dxiˆˆ dy j , dz kˆ } are drawn from the small coordinate corner and highlighted. Then, the remaining 9 edges are added. Volumes and areas are easy because the components of the line element are mutually perpendicular. ˆ Exercise: Consider an area element dAy j . Compute the volume that is swept out by the area as it is given each of the following displacements: dxiˆˆ,and dy j dz kˆ . Prepare sketches. Direction Cosines: A general direction is expressed as: eieijejkekˆˆ(ˆˆˆ ) ( ˆ ) ˆ (ˆˆ ˆ ) (cos ) iˆ (cos ) ˆj (cos ) k ˆ where cos, cos and cos are the direction cosines of with respect to the three coordinate directions. That is cos = ieˆ ˆ the cosine of the angle between the direction of eˆ and that of iˆ , the x direction. CS 4 Coordinate Systems Cylindrical Coordinates Orientation relative to the Cartesian standard system: The origins and z axes of the cylindrical system and of the Cartesian reference are coincident. The cylindrical radial coordinate is the perpendicular distance from the point to the z axis. The angle is the angle between the x axis and the projection of the position vector in the x-y plane. Coordinate ranges: 0 r < ∞, 0 < 2π, and -∞ < z < ∞. NOTATION ALERT: The radial coordinate r represents the distance from the axis in the cylindrical system. It is chosen to coincide with the standard notation used for 2D polar coordinates. This notation has a potential pitfall as r rrz22 , and it can be confused with the spherical radial coordinate r = r , the distance from the origin. Stay Alert! Why do we use this ambiguous notation? Unfortunately, there is no uniformly adopted notation that avoids the potential for confusion. Some authors use or perhaps s for the cylindrical radial coordinate, but just as many use r. The symbols and s are also multiply assigned as charge or mass densities or as distance. It is therefore the choice of this author to follow the common practice of using r.
Load more

Recommended publications
  • Chapter 11. Three Dimensional Analytic Geometry and Vectors
    Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1.
    [Show full text]
  • An Introduction to Topology the Classification Theorem for Surfaces by E
    An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5.
    [Show full text]
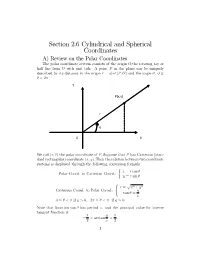
  • Section 2.6 Cylindrical and Spherical Coordinates
    Section 2.6 Cylindrical and Spherical Coordinates A) Review on the Polar Coordinates The polar coordinate system consists of the origin O,the rotating ray or half line from O with unit tick. A point P in the plane can be uniquely described by its distance to the origin r = dist (P, O) and the angle µ, 0 µ < 2¼ : · Y P(x,y) r θ O X We call (r, µ) the polar coordinate of P. Suppose that P has Cartesian (stan- dard rectangular) coordinate (x, y) .Then the relation between two coordinate systems is displayed through the following conversion formula: x = r cos µ Polar Coord. to Cartesian Coord.: y = r sin µ ½ r = x2 + y2 Cartesian Coord. to Polar Coord.: y tan µ = ( p x 0 µ < ¼ if y > 0, 2¼ µ < ¼ if y 0. · · · Note that function tan µ has period ¼, and the principal value for inverse tangent function is ¼ y ¼ < arctan < . ¡ 2 x 2 1 So the angle should be determined by y arctan , if x > 0 xy 8 arctan + ¼, if x < 0 µ = > ¼ x > > , if x = 0, y > 0 < 2 ¼ , if x = 0, y < 0 > ¡ 2 > > Example 6.1. Fin:>d (a) Cartesian Coord. of P whose Polar Coord. is ¼ 2, , and (b) Polar Coord. of Q whose Cartesian Coord. is ( 1, 1) . 3 ¡ ¡ ³ So´l. (a) ¼ x = 2 cos = 1, 3 ¼ y = 2 sin = p3. 3 (b) r = p1 + 1 = p2 1 ¼ ¼ 5¼ tan µ = ¡ = 1 = µ = or µ = + ¼ = . 1 ) 4 4 4 ¡ 5¼ Since ( 1, 1) is in the third quadrant, we choose µ = so ¡ ¡ 4 5¼ p2, is Polar Coord.
    [Show full text]
  • Area, Volume and Surface Area
    The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 11 AREA, VOLUME AND SURFACE AREA A guide for teachers - Years 8–10 June 2011 YEARS 810 Area, Volume and Surface Area (Measurement and Geometry: Module 11) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the international Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 11 AREA, VOLUME AND SURFACE AREA A guide for teachers - Years 8–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 810 {4} A guide for teachers AREA, VOLUME AND SURFACE AREA ASSUMED KNOWLEDGE • Knowledge of the areas of rectangles, triangles, circles and composite figures. • The definitions of a parallelogram and a rhombus. • Familiarity with the basic properties of parallel lines. • Familiarity with the volume of a rectangular prism. • Basic knowledge of congruence and similarity. • Since some formulas will be involved, the students will need some experience with substitution and also with the distributive law.
    [Show full text]
  • Assignment: 14 Subject: - Social Science Class: - VI Teacher: - Mrs
    Assignment: 14 Subject: - Social Science Class: - VI Teacher: - Mrs. Shilpa Grover Name: ______________ Class & Sec: _______________ Roll No. ______ Date: 23.05.2020 GEOGRAPHY QUESTIONS CHAPTER-2 A. Define the following terms: 1. Equator: It is an imaginary line drawn midway between the North and South Poles. It divides the Earth into two equal parts, the North Hemisphere and the South Hemisphere. 2. Earth’s grid: The network of parallels or latitudes and meridians or longitudes that divide the Earth’s surface into a grid-like pattern is called the Earth’s grid or geographic grid. 3. Heat zones: The Earth is divided into three heat zones based on the amount of heat each part receives from the Sun. These three heat zones are the Torrid Zone, the Temperate Zone and the Frigid Zone. 4. Great circle: The Equator is known as the great circle, as it is the largest circle that can be drawn on the globe. This is because the equatorial diameter of the Earth is the largest. 5. Prime Meridian: It is the longitude that passes through Greenwich, a place near London in the UK. It is treated as the reference point. Places to the east and west of the Prime Meridian are measured in degrees. 6. Time zones: A time zone is a narrow belt of the Earth’s surface, which has an east‒west extent of 15 degrees of longitude. The world has been divided into 24 standard time zones. B. Answer the following Questions: 1. What is the true shape of the Earth? The Earth looks spherical in shape, but it is slightly flattened at the North and South Poles and bulges at the equator due to the outward force caused by the rotation of the Earth.
    [Show full text]
  • Line Element in Noncommutative Geometry
    Line element in noncommutative geometry P. Martinetti G¨ottingenUniversit¨at Wroclaw, July 2009 . ? ? - & ? !? The line element p µ ν ds = gµν dx dx is mainly useful to measure distance Z y d(x; y) = inf ds: x If, for some quantum gravity reasons, [x µ; x ν ] 6= 0 is one losing the notion of distance ? (annoying then to speak of noncommutative geo-metry). ? - . ? !? The line element p µ ν ds = gµν dx dx & ? is mainly useful to measure distance Z y d(x; y) = inf ds: x If, for some quantum gravity reasons, [x µ; x ν ] 6= 0 is one losing the notion of distance ? (annoying then to speak of noncommutative geo-metry). ? - !? The line element p µ ν ds = gµν dx dx . & ? ? is mainly useful to measure distance Z y d(x; y) = inf ds: x If, for some quantum gravity reasons, [x µ; x ν ] 6= 0 is one losing the notion of distance ? (annoying then to speak of noncommutative geo-metry). ? - The line element p µ ν ds = gµν dx dx . & ? ? is mainly useful to measure distance Z y !? d(x; y) = inf ds: x If, for some quantum gravity reasons, [x µ; x ν ] 6= 0 is one losing the notion of distance ? (annoying then to speak of noncommutative geo-metry). The line element p µ ν ds = gµν dx dx . & ? ? is mainly useful to measure distance ? -Z y !? d(x; y) = inf ds: x If, for some quantum gravity reasons, [x µ; x ν ] 6= 0 is one losing the notion of distance ? (annoying then to speak of noncommutative geo-metry).
    [Show full text]
  • Analytic Geometry
    STATISTIC ANALYTIC GEOMETRY SESSION 3 STATISTIC SESSION 3 Session 3 Analytic Geometry Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D) Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2D Shapes Activity: Sorting Shapes Triangles Right Angled Triangles Interactive Triangles Quadrilaterals (Rhombus, Parallelogram, etc) Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite Interactive Quadrilaterals Shapes Freeplay Perimeter Area Area of Plane Shapes Area Calculation Tool Area of Polygon by Drawing Activity: Garden Area General Drawing Tool Polygons A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons. Here are some more: Pentagon Pentagra m Hexagon Properties of Regular Polygons Diagonals of Polygons Interactive Polygons The Circle Circle Pi Circle Sector and Segment Circle Area by Sectors Annulus Activity: Dropping a Coin onto a Grid Circle Theorems (Advanced Topic) Symbols There are many special symbols used in Geometry. Here is a short reference for you:
    [Show full text]
  • Surface Topology
    2 Surface topology 2.1 Classification of surfaces In this second introductory chapter, we change direction completely. We dis- cuss the topological classification of surfaces, and outline one approach to a proof. Our treatment here is almost entirely informal; we do not even define precisely what we mean by a ‘surface’. (Definitions will be found in the following chapter.) However, with the aid of some more sophisticated technical language, it not too hard to turn our informal account into a precise proof. The reasons for including this material here are, first, that it gives a counterweight to the previous chapter: the two together illustrate two themes—complex analysis and topology—which run through the study of Riemann surfaces. And, second, that we are able to introduce some more advanced ideas that will be taken up later in the book. The statement of the classification of closed surfaces is probably well known to many readers. We write down two families of surfaces g, h for integers g ≥ 0, h ≥ 1. 2 2 The surface 0 is the 2-sphere S . The surface 1 is the 2-torus T .For g ≥ 2, we define the surface g by taking the ‘connected sum’ of g copies of the torus. In general, if X and Y are (connected) surfaces, the connected sum XY is a surface constructed as follows (Figure 2.1). We choose small discs DX in X and DY in Y and cut them out to get a pair of ‘surfaces-with- boundaries’, coresponding to the circle boundaries of DX and DY.
    [Show full text]
  • Chapter Outline Thinking Ahead 4 EARTH, MOON, AND
    Chapter 4 Earth, Moon, and Sky 103 4 EARTH, MOON, AND SKY Figure 4.1 Southern Summer. As captured with a fish-eye lens aboard the Atlantis Space Shuttle on December 9, 1993, Earth hangs above the Hubble Space Telescope as it is repaired. The reddish continent is Australia, its size and shape distorted by the special lens. Because the seasons in the Southern Hemisphere are opposite those in the Northern Hemisphere, it is summer in Australia on this December day. (credit: modification of work by NASA) Chapter Outline 4.1 Earth and Sky 4.2 The Seasons 4.3 Keeping Time 4.4 The Calendar 4.5 Phases and Motions of the Moon 4.6 Ocean Tides and the Moon 4.7 Eclipses of the Sun and Moon Thinking Ahead If Earth’s orbit is nearly a perfect circle (as we saw in earlier chapters), why is it hotter in summer and colder in winter in many places around the globe? And why are the seasons in Australia or Peru the opposite of those in the United States or Europe? The story is told that Galileo, as he left the Hall of the Inquisition following his retraction of the doctrine that Earth rotates and revolves about the Sun, said under his breath, “But nevertheless it moves.” Historians are not sure whether the story is true, but certainly Galileo knew that Earth was in motion, whatever church authorities said. It is the motions of Earth that produce the seasons and give us our measures of time and date. The Moon’s motions around us provide the concept of the month and the cycle of lunar phases.
    [Show full text]
  • Reference Systems for Surveying and Mapping Lecture Notes
    Delft University of Technology Reference Systems for Surveying and Mapping Lecture notes Hans van der Marel ii The front cover shows the NAP (Amsterdam Ordnance Datum) ”datum point” at the Stopera, Amsterdam (picture M.M.Minderhoud, Wikipedia/Michiel1972). H. van der Marel Lecture notes on Reference Systems for Surveying and Mapping: CTB3310 Surveying and Mapping CTB3425 Monitoring and Stability of Dikes and Embankments CIE4606 Geodesy and Remote Sensing CIE4614 Land Surveying and Civil Infrastructure February 2020 Publisher: Faculty of Civil Engineering and Geosciences Delft University of Technology P.O. Box 5048 Stevinweg 1 2628 CN Delft The Netherlands Copyright ©2014­2020 by H. van der Marel The content in these lecture notes, except for material credited to third parties, is licensed under a Creative Commons Attributions­NonCommercial­SharedAlike 4.0 International License (CC BY­NC­SA). Third party material is shared under its own license and attribution. The text has been type set using the MikTex 2.9 implementation of LATEX. Graphs and diagrams were produced, if not mentioned otherwise, with Matlab and Inkscape. Preface This reader on reference systems for surveying and mapping has been initially compiled for the course Surveying and Mapping (CTB3310) in the 3rd year of the BSc­program for Civil Engineering. The reader is aimed at students at the end of their BSc program or at the start of their MSc program, and is used in several courses at Delft University of Technology. With the advent of the Global Positioning System (GPS) technology in mobile (smart) phones and other navigational devices almost anyone, anywhere on Earth, and at any time, can determine a three–dimensional position accurate to a few meters.
    [Show full text]
  • Educator Guide
    E DUCATOR GUIDE This guide, and its contents, are Copyrighted and are the sole Intellectual Property of Science North. E DUCATOR GUIDE The Arctic has always been a place of mystery, myth and fascination. The Inuit and their predecessors adapted and thrived for thousands of years in what is arguably the harshest environment on earth. Today, the Arctic is the focus of intense research. Instead of seeking to conquer the north, scientist pioneers are searching for answers to some troubling questions about the impacts of human activities around the world on this fragile and largely uninhabited frontier. The giant screen film, Wonders of the Arctic, centers on our ongoing mission to explore and come to terms with the Arctic, and the compelling stories of our many forays into this captivating place will be interwoven to create a unifying message about the state of the Arctic today. Underlying all these tales is the crucial role that ice plays in the northern environment and the changes that are quickly overtaking the people and animals who have adapted to this land of ice and snow. This Education Guide to the Wonders of the Arctic film is a tool for educators to explore the many fascinating aspects of the Arctic. This guide provides background information on Arctic geography, wildlife and the ice, descriptions of participatory activities, as well as references and other resources. The guide may be used to prepare the students for the film, as a follow up to the viewing, or to simply stimulate exploration of themes not covered within the film.
    [Show full text]
  • THE EARTH. MERIDIANS and PARALLELS 2=Meridian (Geography)
    THE EARTH. MERIDIANS AND PARALLELS 1=Circle of latitude 2=Meridian (geography) A circle of latitude , on the Earth , is an imaginary east -west circle connecting all locations (not taking into account elevation) that share a given latitude . A location's position along a circle of latitude is given by its longitude . Circles of latitude are often called parallels because they are parallel to each other. On some map projections, including the Equirectangular projection , they are drawn at equidistant intervals. Circles of latitude become smaller the farther they are from the equator and the closer they are to the poles . A circle of latitude is perpendicular to all meridians at the points of intersection, and is hence a special case of a loxodrome . Contrary to what might be assumed from their straight-line representation on some map projections, a circle of latitude is not, with the sole exception of the Equator, the shortest distance between two points lying on the Earth. In other words, circles of latitude (except for the Equator) are not great circles (see also great-circle distance ). It is for this reason that an airplane traveling between a European and North American city that share the same latitude will fly farther north, over Greenland for example. Arcs of circles of latitude are sometimes used as boundaries between countries or regions where distinctive natural borders are lacking (such as in deserts), or when an artificial border is drawn as a "line on a map", as happened in Korea . Longitude (λ) Lines of longitude appear vertical with varying curvature in this projection; but are actually halves of great ellipses, with identical radii at a given latitude.
    [Show full text]