DOCSLIB.ORG

Math 254A. the Discriminant of Xn + Ax + B

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Math 254A. the Discriminant of Xn + Ax + B Math 254A. The Discriminant of xn + ax + b The discriminant of a polynomial f of degree n is a homogeneous polynomial of degree n(n − 1) in the roots of f . By Lang's Algebra, Ch. IV Thm. 6.1, this discriminant is also a polynomial in the coefficients a , b of f . These coefficients are homogeneous polynomials of degrees n−1 and n in the roots of f , so the discriminant is a weighted homogeneous polynomial φ of degree n(n − 1) in a and b , where a has weight n − 1 and b has weight n . Therefore any monomial aibj occurring in φ must have (n − 1)i + nj = n(n − 1) . There are only two possibilities with i ≥ 0 and j ≥ 0 , namely (i; j) = (0; n − 1) and (i; j) = (n; 0) , so the discriminant is of the form D = αan + βbn−1 : (*) We first restrict to working over C . We start by finding the coefficient β . This can be found by computing the discrim- inant of the polynomial xn − 1 , which has roots 1; ζ; : : : ; ζn−1 , where ζ is a primitive nth root of unity. We have Y i j 2 Dxn−1 = (ζ − ζ ) 0≤i<j<n n−1 Y Y = (−1)n(n−1)=2 (ζi − ζj) i=0 0≤j<n j6=i n−1 n−1 Y Y = (−1)n(n−1)=2 (ζi − ζi+`) i=0 `=1 n−1 ! n−1 !n Y Y = (−1)n(n−1)=2 ζi(n−1) (1 − ζ`) : i=0 `=1 2 The first product in this expression is ζn(n−1) =2 . If n is odd, then (n − 1)2=2 2 Z , and the product is 1 ; if n is even, then this is an odd power of ζn=2 = −1 . Thus, the first product is (−1)n−1 . The second product equals n , because it is the value of the polynomial xn − 1 = xn−1 + ··· + 1 ; x − 1 evaluated at x = 1 . Thus n(n−1)=2 n−1 n Dxn−1 = (−1) (−1) n ; and since this equals (−1)n−1β , we have β = (−1)n(n−1)=2nn : 2 Next we find the coefficient α , this time using the polynomial xn − x . This polynomial has roots 0 , ζ0 , ζ1 , ::: , ζn−2 , where ζ is now a primitive (n − 1)st root of unity. The discriminant of this polynomial is therefore n−2 Y i 2 Y i j 2 Dxn−x = (ζ − 0) · (ζ − ζ ) i=0 0≤i<n−1 0≤j<n−1 i<j = ζ(n−1)(n−2) · (discriminant of xn−1 − 1) = (−1)(n−1)(n−2)=2(−1)n−2(n − 1)n−1 = −(−1)n(n−1)=2(n − 1)n−1 : This equals (−1)nα , so α = (−1)n(n−1)=2(1 − n)n−1 : By (*), we then have D = (−1)n(n−1)=2(1 − n)n−1an + nnbn−1 : (**) The above computation determined the discriminant for polynomials of the above form over C . But the discriminant of a polynomial of the form xn + ax + b over an arbitrary commutative ring A is of the form φ(a; b) for some polynomial φ 2 A[t; u]; moreover, by functoriality, if α: A ! B is a homomorphism of commutative rings, then the polynomials φA(t; u) and φB(t; u) giving discriminants of polynomials of the α given form with coefficients in A and B , respectively, are related by φB = φA . Thus, (**) gives the discriminant for polynomials xn + ax + b in Z[x] and (via the unique map Z ! A ) it also gives the discriminant for arbitrary commutative rings A ..
Load more

Recommended publications
  • Homogeneous Polynomial Solutions to Constant Coefficient Pde’S
    HOMOGENEOUS POLYNOMIAL SOLUTIONS TO CONSTANT COEFFICIENT PDE'S Bruce Reznick University of Illinois 1409 W. Green St. Urbana, IL 61801 [email protected] October 21, 1994 1. Introduction Suppose p is a homogeneous polynomial over a field K. Let p(D) be the differen- @ tial operator defined by replacing each occurence of xj in p by , defined formally @xj 2 in case K is not a subset of C. (The classical example is p(x1; · · · ; xn) = j xj , for which p(D) is the Laplacian r2.) In this paper we solve the equation p(DP)q = 0 for homogeneous polynomials q over K, under the restriction that K be an algebraically closed field of characteristic 0. (This restriction is mild, considering that the \natu- ral" field is C.) Our Main Theorem and its proof are the natural extensions of work by Sylvester, Clifford, Rosanes, Gundelfinger, Cartan, Maass and Helgason. The novelties in the presentation are the generalization of the base field and the removal of some restrictions on p. The proofs require only undergraduate mathematics and Hilbert's Nullstellensatz. A fringe benefit of the proof of the Main Theorem is an Expansion Theorem for homogeneous polynomials over R and C. This theorem is 2 2 2 trivial for linear forms, goes back at least to Gauss for p = x1 + x2 + x3, and has also been studied by Maass and Helgason. Main Theorem (See Theorem 4.1). Let K be an algebraically closed field of mj characteristic 0. Suppose p 2 K[x1; · · · ; xn] is homogeneous and p = j pj for distinct non-constant irreducible factors pj 2 K[x1; · · · ; xn].
    [Show full text]
  • Solving Cubic Polynomials
    Solving Cubic Polynomials 1.1 The general solution to the quadratic equation There are four steps to finding the zeroes of a quadratic polynomial. 1. First divide by the leading term, making the polynomial monic. a 2. Then, given x2 + a x + a , substitute x = y − 1 to obtain an equation without the linear term. 1 0 2 (This is the \depressed" equation.) 3. Solve then for y as a square root. (Remember to use both signs of the square root.) a 4. Once this is done, recover x using the fact that x = y − 1 . 2 For example, let's solve 2x2 + 7x − 15 = 0: First, we divide both sides by 2 to create an equation with leading term equal to one: 7 15 x2 + x − = 0: 2 2 a 7 Then replace x by x = y − 1 = y − to obtain: 2 4 169 y2 = 16 Solve for y: 13 13 y = or − 4 4 Then, solving back for x, we have 3 x = or − 5: 2 This method is equivalent to \completing the square" and is the steps taken in developing the much- memorized quadratic formula. For example, if the original equation is our \high school quadratic" ax2 + bx + c = 0 then the first step creates the equation b c x2 + x + = 0: a a b We then write x = y − and obtain, after simplifying, 2a b2 − 4ac y2 − = 0 4a2 so that p b2 − 4ac y = ± 2a and so p b b2 − 4ac x = − ± : 2a 2a 1 The solutions to this quadratic depend heavily on the value of b2 − 4ac.
    [Show full text]
  • Algebra Polynomial(Lecture-I)
    Algebra Polynomial(Lecture-I) Dr. Amal Kumar Adak Department of Mathematics, G.D.College, Begusarai March 27, 2020 Algebra Dr. Amal Kumar Adak Definition Function: Any mathematical expression involving a quantity (say x) which can take different values, is called a function of that quantity. The quantity (x) is called the variable and the function of it is denoted by f (x) ; F (x) etc. Example:f (x) = x2 + 5x + 6 + x6 + x3 + 4x5. Algebra Dr. Amal Kumar Adak Polynomial Definition Polynomial: A polynomial in x over a real or complex field is an expression of the form n n−1 n−3 p (x) = a0x + a1x + a2x + ::: + an,where a0; a1;a2; :::; an are constants (free from x) may be real or complex and n is a positive integer. Example: (i)5x4 + 4x3 + 6x + 1,is a polynomial where a0 = 5; a1 = 4; a2 = 0; a3 = 6; a4 = 1a0 = 4; a1 = 4; 2 1 3 3 2 1 (ii)x + x + x + 2 is not a polynomial, since 3 ; 3 are not integers. (iii)x4 + x3 cos (x) + x2 + x + 1 is not a polynomial for the presence of the term cos (x) Algebra Dr. Amal Kumar Adak Definition Zero Polynomial: A polynomial in which all the coefficients a0; a1; a2; :::; an are zero is called a zero polynomial. Definition Complete and Incomplete polynomials: A polynomial with non-zero coefficients is called a complete polynomial. Other-wise it is incomplete. Example of a complete polynomial:x5 + 2x4 + 3x3 + 7x2 + 9x + 1. Example of an incomplete polynomial: x5 + 3x3 + 7x2 + 9x + 1.
    [Show full text]
  • Elements of Chapter 9: Nonlinear Systems Examples
    Elements of Chapter 9: Nonlinear Systems To solve x0 = Ax, we use the ansatz that x(t) = eλtv. We found that λ is an eigenvalue of A, and v an associated eigenvector. We can also summarize the geometric behavior of the solutions by looking at a plot- However, there is an easier way to classify the stability of the origin (as an equilibrium), To find the eigenvalues, we compute the characteristic equation: p Tr(A) ± ∆ λ2 − Tr(A)λ + det(A) = 0 λ = 2 which depends on the discriminant ∆: • ∆ > 0: Real λ1; λ2. • ∆ < 0: Complex λ = a + ib • ∆ = 0: One eigenvalue. The type of solution depends on ∆, and in particular, where ∆ = 0: ∆ = 0 ) 0 = (Tr(A))2 − 4det(A) This is a parabola in the (Tr(A); det(A)) coordinate system, inside the parabola is where ∆ < 0 (complex roots), and outside the parabola is where ∆ > 0. We can then locate the position of our particular trace and determinant using the Poincar´eDiagram and it will tell us what the stability will be. Examples Given the system where x0 = Ax for each matrix A below, classify the origin using the Poincar´eDiagram: 1 −4 1. 4 −7 SOLUTION: Compute the trace, determinant and discriminant: Tr(A) = −6 Det(A) = −7 + 16 = 9 ∆ = 36 − 4 · 9 = 0 Therefore, we have a \degenerate sink" at the origin. 1 2 2. −5 −1 SOLUTION: Compute the trace, determinant and discriminant: Tr(A) = 0 Det(A) = −1 + 10 = 9 ∆ = 02 − 4 · 9 = −36 The origin is a center. 1 3. Given the system x0 = Ax where the matrix A depends on α, describe how the equilibrium solution changes depending on α (use the Poincar´e Diagram): 2 −5 (a) α −2 SOLUTION: The trace is 0, so that puts us on the \det(A)" axis.
    [Show full text]
  • Quadratic Form - Wikipedia, the Free Encyclopedia
    Quadratic form - Wikipedia, the free encyclopedia http://en.wikipedia.org/wiki/Quadratic_form Quadratic form From Wikipedia, the free encyclopedia In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example, is a quadratic form in the variables x and y. Quadratic forms occupy a central place in various branches of mathematics, including number theory, linear algebra, group theory (orthogonal group), differential geometry (Riemannian metric), differential topology (intersection forms of four-manifolds), and Lie theory (the Killing form). Contents 1 Introduction 2 History 3 Real quadratic forms 4 Definitions 4.1 Quadratic spaces 4.2 Further definitions 5 Equivalence of forms 6 Geometric meaning 7 Integral quadratic forms 7.1 Historical use 7.2 Universal quadratic forms 8 See also 9 Notes 10 References 11 External links Introduction Quadratic forms are homogeneous quadratic polynomials in n variables. In the cases of one, two, and three variables they are called unary, binary, and ternary and have the following explicit form: where a,…,f are the coefficients.[1] Note that quadratic functions, such as ax2 + bx + c in the one variable case, are not quadratic forms, as they are typically not homogeneous (unless b and c are both 0). The theory of quadratic forms and methods used in their study depend in a large measure on the nature of the 1 of 8 27/03/2013 12:41 Quadratic form - Wikipedia, the free encyclopedia http://en.wikipedia.org/wiki/Quadratic_form coefficients, which may be real or complex numbers, rational numbers, or integers. In linear algebra, analytic geometry, and in the majority of applications of quadratic forms, the coefficients are real or complex numbers.
    [Show full text]
  • Polynomials and Quadratics
    Higher hsn .uk.net Mathematics UNIT 2 OUTCOME 1 Polynomials and Quadratics Contents Polynomials and Quadratics 64 1 Quadratics 64 2 The Discriminant 66 3 Completing the Square 67 4 Sketching Parabolas 70 5 Determining the Equation of a Parabola 72 6 Solving Quadratic Inequalities 74 7 Intersections of Lines and Parabolas 76 8 Polynomials 77 9 Synthetic Division 78 10 Finding Unknown Coefficients 82 11 Finding Intersections of Curves 84 12 Determining the Equation of a Curve 86 13 Approximating Roots 88 HSN22100 This document was produced specially for the HSN.uk.net website, and we require that any copies or derivative works attribute the work to Higher Still Notes. For more details about the copyright on these notes, please see http://creativecommons.org/licenses/by-nc-sa/2.5/scotland/ Higher Mathematics Unit 2 – Polynomials and Quadratics OUTCOME 1 Polynomials and Quadratics 1 Quadratics A quadratic has the form ax2 + bx + c where a, b, and c are any real numbers, provided a ≠ 0 . You should already be familiar with the following. The graph of a quadratic is called a parabola . There are two possible shapes: concave up (if a > 0 ) concave down (if a < 0 ) This has a minimum This has a maximum turning point turning point To find the roots (i.e. solutions) of the quadratic equation ax2 + bx + c = 0, we can use: factorisation; completing the square (see Section 3); −b ± b2 − 4 ac the quadratic formula: x = (this is not given in the exam). 2a EXAMPLES 1. Find the roots of x2 −2 x − 3 = 0 .
    [Show full text]
  • Solving Quadratic Equations in Many Variables
    Snapshots of modern mathematics № 12/2017 from Oberwolfach Solving quadratic equations in many variables Jean-Pierre Tignol 1 Fields are number systems in which every linear equa- tion has a solution, such as the set of all rational numbers Q or the set of all real numbers R. All fields have the same properties in relation with systems of linear equations, but quadratic equations behave dif- ferently from field to field. Is there a field in which every quadratic equation in five variables has a solu- tion, but some quadratic equation in four variables has no solution? The answer is in this snapshot. 1 Fields No problem is more fundamental to algebra than solving polynomial equations. Indeed, the name algebra itself derives from a ninth century treatise [1] where the author explains how to solve quadratic equations like x2 +10x = 39. It was clear from the start that some equations with integral coefficients like x2 = 2 may not have any integral solution. Even allowing positive and negative numbers with infinite decimal expansion as solutions (these numbers are called real numbers), one cannot solve x2 = −1 because the square of every real number is positive or zero. However, it is only a small step from the real numbers to the solution 1 Jean-Pierre Tignol acknowledges support from the Fonds de la Recherche Scientifique (FNRS) under grant n◦ J.0014.15. He is grateful to Karim Johannes Becher, Andrew Dolphin, and David Leep for comments on a preliminary version of this text. 1 of every polynomial equation: one gives the solution of the equation x2 = −1 (or x2 + 1 = 0) the name i and defines complex numbers as expressions of the form a + bi, where a and b are real numbers.
    [Show full text]
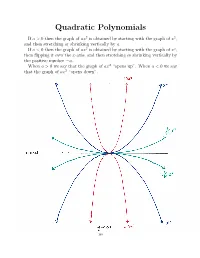
  • Quadratic Polynomials
    Quadratic Polynomials If a>0thenthegraphofax2 is obtained by starting with the graph of x2, and then stretching or shrinking vertically by a. If a<0thenthegraphofax2 is obtained by starting with the graph of x2, then flipping it over the x-axis, and then stretching or shrinking vertically by the positive number a. When a>0wesaythatthegraphof− ax2 “opens up”. When a<0wesay that the graph of ax2 “opens down”. I Cit i-a x-ax~S ~12 *************‘s-aXiS —10.? 148 2 If a, c, d and a = 0, then the graph of a(x + c) 2 + d is obtained by If a, c, d R and a = 0, then the graph of a(x + c)2 + d is obtained by 2 R 6 2 shiftingIf a, c, the d ⇥ graphR and ofaax=⇤ 2 0,horizontally then the graph by c, and of a vertically(x + c) + byd dis. obtained (Remember by shiftingshifting the the⇥ graph graph of of axax⇤ 2 horizontallyhorizontally by by cc,, and and vertically vertically by by dd.. (Remember (Remember thatthatd>d>0meansmovingup,0meansmovingup,d<d<0meansmovingdown,0meansmovingdown,c>c>0meansmoving0meansmoving thatleft,andd>c<0meansmovingup,0meansmovingd<right0meansmovingdown,.) c>0meansmoving leftleft,and,andc<c<0meansmoving0meansmovingrightright.).) 2 If a =0,thegraphofafunctionf(x)=a(x + c) 2+ d is called a parabola. If a =0,thegraphofafunctionf(x)=a(x + c)2 + d is called a parabola. 6 2 TheIf a point=0,thegraphofafunction⇤ ( c, d) 2 is called thefvertex(x)=aof(x the+ c parabola.) + d is called a parabola. The point⇤ ( c, d) R2 is called the vertex of the parabola.
    [Show full text]
  • Degree Bounds for Gröbner Bases in Algebras of Solvable Type
    Degree Bounds for Gröbner Bases in Algebras of Solvable Type Matthias Aschenbrenner University of California, Los Angeles (joint with Anton Leykin) Algebras of Solvable Type • . introduced by Kandri-Rody & Weispfenning (1990); • . form a class of associative algebras over fields which generalize • commutative polynomial rings; • Weyl algebras; • universal enveloping algebras of f. d. Lie algebras; • . are sometimes also called polynomial rings of solvable type or PBW-algebras (Poincaré-Birkhoff-Witt). Weyl Algebras Systems of linear PDE with polynomial coefficients can be represented by left ideals in the Weyl algebra An(C) = Chx1,..., xn, ∂1, . , ∂ni, the C-algebra generated by the xi , ∂j subject to the relations: xj xi = xi xj , ∂j ∂i = ∂i ∂j and ( xi ∂j if i 6= j ∂j xi = xi ∂j + 1 if i = j. The Weyl algebra acts naturally on C[x1,..., xn]: ∂f (∂i , f ) 7→ , (xi , f ) 7→ xi f . ∂xi Universal Enveloping Algebras Let g be a Lie algebra over a field K . The universal enveloping algebra U(g) of g is the K -algebra obtained by imposing the relations g ⊗ h − h ⊗ g = [g, h]g on the tensor algebra of the K -linear space g. Poincaré-Birkhoff-Witt Theorem: the canonical morphism g → U(g) is injective, and g generates the K -algebra U(g). If g corresponds to a Lie group G, then U(g) can be identified with the algebra of left-invariant differential operators on G. Affine Algebras and Monomials N Let R be a K -algebra, and x = (x1,..., xN ) ∈ R . Write α α1 αN N x := x1 ··· xN for a multi-index α = (α1, .
    [Show full text]
  • Hyperbolicity and Stable Polynomials in Combinatorics and Probability
    Hyperbolicity and stable polynomials in combinatorics and probability Robin Pemantle 1,2 ABSTRACT: These lectures survey the theory of hyperbolic and stable polynomials, from their origins in the theory of linear PDE’s to their present uses in combinatorics and probability theory. Keywords: amoeba, cone, dual cone, G˚arding-hyperbolicity, generating function, half-plane prop- erty, homogeneous polynomial, Laguerre–P´olya class, multiplier sequence, multi-affine, multivariate stability, negative dependence, negative association, Newton’s inequalities, Rayleigh property, real roots, semi-continuity, stochastic covering, stochastic domination, total positivity. Subject classification: Primary: 26C10, 62H20; secondary: 30C15, 05A15. 1Supported in part by National Science Foundation grant # DMS 0905937 2University of Pennsylvania, Department of Mathematics, 209 S. 33rd Street, Philadelphia, PA 19104 USA, pe- [email protected] Contents 1 Introduction 1 2 Origins, definitions and properties 4 2.1 Relation to the propagation of wave-like equations . 4 2.2 Homogeneous hyperbolic polynomials . 7 2.3 Cones of hyperbolicity for homogeneous polynomials . 10 3 Semi-continuity and Morse deformations 14 3.1 Localization . 14 3.2 Amoeba boundaries . 15 3.3 Morse deformations . 17 3.4 Asymptotics of Taylor coefficients . 19 4 Stability theory in one variable 23 4.1 Stability over general regions . 23 4.2 Real roots and Newton’s inequalities . 26 4.3 The Laguerre–P´olya class . 31 5 Multivariate stability 34 5.1 Equivalences . 36 5.2 Operations preserving stability . 38 5.3 More closure properties . 41 6 Negative dependence 41 6.1 A brief history of negative dependence . 41 6.2 Search for a theory . 43 i 6.3 The grail is found: application of stability theory to joint laws of binary random variables .
    [Show full text]
  • The Determinant and the Discriminant
    CHAPTER 2 The determinant and the discriminant In this chapter we discuss two indefinite quadratic forms: the determi- nant quadratic form det(a, b, c, d)=ad bc, − and the discriminant disc(a, b, c)=b2 4ac. − We will be interested in the integral representations of a given integer n by either of these, that is the set of solutions of the equations 4 ad bc = n, (a, b, c, d) Z − 2 and 2 3 b ac = n, (a, b, c) Z . − 2 For q either of these forms, we denote by Rq(n) the set of all such represen- tations. Consider the three basic questions of the previous chapter: (1) When is Rq(n) non-empty ? (2) If non-empty, how large Rq(n)is? (3) How is the set Rq(n) distributed as n varies ? In a suitable sense, a good portion of the answers to these question will be similar to the four and three square quadratic forms; but there will be major di↵erences coming from the fact that – det and disc are indefinite quadratic forms (have signature (2, 2) and (2, 1) over the reals), – det and disc admit isotropic vectors: there exist x Q4 (resp. Q3) such that det(x)=0(resp.disc(x) = 0). 2 1. Existence and number of representations by the determinant As the name suggest, determining Rdet(n) is equivalent to determining the integral 2 2 matrices of determinant n: ⇥ (n) ab Rdet(n) M (Z)= g = M2(Z), det(g)=n . ' 2 { cd 2 } ✓ ◆ n 0 Observe that the diagonal matrix a = has determinant n, and any 01 ✓ ◆ other matrix in the orbit SL2(Z).a is integral and has the same determinant.
    [Show full text]
  • Nature of the Discriminant
    Name: ___________________________ Date: ___________ Class Period: _____ Nature of the Discriminant Quadratic − b b 2 − 4ac x = b2 − 4ac Discriminant Formula 2a The discriminant predicts the “nature of the roots of a quadratic equation given that a, b, and c are rational numbers. It tells you the number of real roots/x-intercepts associated with a quadratic function. Value of the Example showing nature of roots of Graph indicating x-intercepts Discriminant b2 – 4ac ax2 + bx + c = 0 for y = ax2 + bx + c POSITIVE Not a perfect x2 – 2x – 7 = 0 2 b – 4ac > 0 square − (−2) (−2)2 − 4(1)(−7) x = 2(1) 2 32 2 4 2 x = = = 1 2 2 2 2 Discriminant: 32 There are two real roots. These roots are irrational. There are two x-intercepts. Perfect square x2 + 6x + 5 = 0 − 6 62 − 4(1)(5) x = 2(1) − 6 16 − 6 4 x = = = −1,−5 2 2 Discriminant: 16 There are two real roots. These roots are rational. There are two x-intercepts. ZERO b2 – 4ac = 0 x2 – 2x + 1 = 0 − (−2) (−2)2 − 4(1)(1) x = 2(1) 2 0 2 x = = = 1 2 2 Discriminant: 0 There is one real root (with a multiplicity of 2). This root is rational. There is one x-intercept. NEGATIVE b2 – 4ac < 0 x2 – 3x + 10 = 0 − (−3) (−3)2 − 4(1)(10) x = 2(1) 3 − 31 3 31 x = = i 2 2 2 Discriminant: -31 There are two complex/imaginary roots. There are no x-intercepts. Quadratic Formula and Discriminant Practice 1.
    [Show full text]