§4 FLOWS with a FREE SURFACE Such Flows Are Conspicuous All Around Us; They Include Water Waves, River Flow Including Flow Over
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fluid Mechanics
FLUID MECHANICS PROF. DR. METİN GÜNER COMPILER ANKARA UNIVERSITY FACULTY OF AGRICULTURE DEPARTMENT OF AGRICULTURAL MACHINERY AND TECHNOLOGIES ENGINEERING 1 1. INTRODUCTION Mechanics is the oldest physical science that deals with both stationary and moving bodies under the influence of forces. Mechanics is divided into three groups: a) Mechanics of rigid bodies, b) Mechanics of deformable bodies, c) Fluid mechanics Fluid mechanics deals with the behavior of fluids at rest (fluid statics) or in motion (fluid dynamics), and the interaction of fluids with solids or other fluids at the boundaries (Fig.1.1.). Fluid mechanics is the branch of physics which involves the study of fluids (liquids, gases, and plasmas) and the forces on them. Fluid mechanics can be divided into two. a)Fluid Statics b)Fluid Dynamics Fluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at rest. It embraces the study of the conditions under which fluids are at rest in stable equilibrium Hydrostatics is fundamental to hydraulics, the engineering of equipment for storing, transporting and using fluids. Hydrostatics offers physical explanations for many phenomena of everyday life, such as why atmospheric pressure changes with altitude, why wood and oil float on water, and why the surface of water is always flat and horizontal whatever the shape of its container. Fluid dynamics is a subdiscipline of fluid mechanics that deals with fluid flow— the natural science of fluids (liquids and gases) in motion. It has several subdisciplines itself, including aerodynamics (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). -

Fluid Viscosity and the Attenuation of Surface Waves: a Derivation Based on Conservation of Energy
INSTITUTE OF PHYSICS PUBLISHING EUROPEAN JOURNAL OF PHYSICS Eur. J. Phys. 25 (2004) 115–122 PII: S0143-0807(04)64480-1 Fluid viscosity and the attenuation of surface waves: a derivation based on conservation of energy FBehroozi Department of Physics, University of Northern Iowa, Cedar Falls, IA 50614, USA Received 9 June 2003 Published 25 November 2003 Online at stacks.iop.org/EJP/25/115 (DOI: 10.1088/0143-0807/25/1/014) Abstract More than a century ago, Stokes (1819–1903)pointed out that the attenuation of surface waves could be exploited to measure viscosity. This paper provides the link between fluid viscosity and the attenuation of surface waves by invoking the conservation of energy. First we calculate the power loss per unit area due to viscous dissipation. Next we calculate the power loss per unit area as manifested in the decay of the wave amplitude. By equating these two quantities, we derive the relationship between the fluid viscosity and the decay coefficient of the surface waves in a transparent way. 1. Introduction Surface tension and gravity govern the propagation of surface waves on fluids while viscosity determines the wave attenuation. In this paper we focus on the relation between viscosity and attenuation of surface waves. More than a century ago, Stokes (1819–1903) pointed out that the attenuation of surface waves could be exploited to measure viscosity [1]. Since then, the determination of viscosity from the damping of surface waves has receivedmuch attention [2–10], particularly because the method presents the possibility of measuring viscosity noninvasively. In his attempt to obtain the functionalrelationship between viscosity and wave attenuation, Stokes observed that the harmonic solutions obtained by solving the Laplace equation for the velocity potential in the absence of viscosity also satisfy the linearized Navier–Stokes equation [11]. -

Lecture 18 Ocean General Circulation Modeling
Lecture 18 Ocean General Circulation Modeling 9.1 The equations of motion: Navier-Stokes The governing equations for a real fluid are the Navier-Stokes equations (con servation of linear momentum and mass mass) along with conservation of salt, conservation of heat (the first law of thermodynamics) and an equation of state. However, these equations support fast acoustic modes and involve nonlinearities in many terms that makes solving them both difficult and ex pensive and particularly ill suited for long time scale calculations. Instead we make a series of approximations to simplify the Navier-Stokes equations to yield the “primitive equations” which are the basis of most general circu lations models. In a rotating frame of reference and in the absence of sources and sinks of mass or salt the Navier-Stokes equations are @ �~v + �~v~v + 2�~ �~v + g�kˆ + p = ~ρ (9.1) t r · ^ r r · @ � + �~v = 0 (9.2) t r · @ �S + �S~v = 0 (9.3) t r · 1 @t �ζ + �ζ~v = ω (9.4) r · cpS r · F � = �(ζ; S; p) (9.5) Where � is the fluid density, ~v is the velocity, p is the pressure, S is the salinity and ζ is the potential temperature which add up to seven dependent variables. 115 12.950 Atmospheric and Oceanic Modeling, Spring '04 116 The constants are �~ the rotation vector of the sphere, g the gravitational acceleration and cp the specific heat capacity at constant pressure. ~ρ is the stress tensor and ω are non-advective heat fluxes (such as heat exchange across the sea-surface).F 9.2 Acoustic modes Notice that there is no prognostic equation for pressure, p, but there are two equations for density, �; one prognostic and one diagnostic. -

Modelling Viscous Free Surface Flow
Chapter 8 Modelling Viscous Free Surface Flow Free surface flows, where a boundary of a fluid body is free to move constrained only by forces across the surface, are possibly the most commonly observed flow phenomenon, with the motion of the free surface readily allowing the observation of flow of the fluid. Flows that are commonly encountered by the layperson include the motion of the surface of a river, the waves on the surface of the ocean, and the more personal flow of that in a cup of tea. From an engineering perspective, flows of interest include the open channel flow of rivers and canals, the erosive forces of waves on the shoreline, and the wakes generated by ships when under way. When modelling these flows, the problems associated with the solution of the Navier–Stokes equations are compounded by the free motion of the surface of the fluid, with the boundaries of the flow domain being a function of the flow structure, and thus an unknown which must be calculated along with the flow field. The movement of the free surface therefore both aids the observation of the flow, and hinders it’s modelling. In this chapter an attempt is made to model the steady flow around a ships hull. The modelling of such a flow is of great interest to Naval Architects, with the ability to predict the resistance of ships allowing the design of more efficient hull forms, whilst the accurate modelling of the ships wake allows the design of hulls that create a smaller disturbance in confined waterways. -

A Simple and Unified Linear Solver for Free-Surface and Pressurized
water Technical Note A Simple and Unified Linear Solver for Free-Surface and Pressurized Mixed Flows in Hydraulic Systems Dechao Hu 1 , Songping Li 1, Shiming Yao 2 and Zhongwu Jin 2,* 1 School of Hydropower and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; [email protected] (D.H.); [email protected] (S.L.) 2 Yangtze River Scientific Research Institute, Wuhan 430010, China; [email protected] * Correspondence: [email protected]; Tel.: +86-027-8282-9873 Received: 19 August 2019; Accepted: 19 September 2019; Published: 23 September 2019 Abstract: A semi–implicit numerical model with a linear solver is proposed for the free-surface and pressurized mixed flows in hydraulic systems. It solves the two flow regimes within a unified formulation, and is much simpler than existing similar models for mixed flows. Using a local linearization and an Eulerian–Lagrangian method, the new model only needs to solve a tridiagonal linear system (arising from velocity-pressure coupling) and is free of iterations. The model is tested using various types of mixed flows, where the simulation results agree with analytical solutions, experiment data and the results reported by former researchers. Sensitivity studies of grid scales and time steps are both performed, where a common grid scale provides grid-independent results and a common time step provides time-step-independent results. Moreover, the model is revealed to achieve stable and accurate simulations at large time steps for which the CFL is greater than 1. In simulations of a challenging case (mixed flows characterized by frequent flow-regime conversions and a closed pipe with wide-top cross-sections), an artificial slot (A-slot) technique is proposed to cope with possible instabilities related to the discontinuous main-diagonal coefficients of the linear system. -

2.016 Hydrodynamics Free Surface Water Waves
2.016 Hydrodynamics Reading #7 2.016 Hydrodynamics Prof. A.H. Techet Fall 2005 Free Surface Water Waves I. Problem setup 1. Free surface water wave problem. In order to determine an exact equation for the problem of free surface gravity waves we will assume potential theory (ideal flow) and ignore the effects of viscosity. Waves in the ocean are not typically uni-directional, but often approach structures from many directions. This complicates the problem of free surface wave analysis, but can be overcome through a series of assumptions. To setup the exact solution to the free surface gravity wave problem we first specify our unknowns: • Velocity Field: V (x, y, z,t ) = ∇φ(x, y, z,t ) • Free surface elevation: η(x, yt, ) • Pressure field: p(xy,,z , t ) version 3.0 updated 8/30/2005 -1- ©2005 A. Techet 2.016 Hydrodynamics Reading #7 Next we need to set up the equations and conditions that govern the problem: • Continuity (Conservation of Mass): ∇=2φ 0 for z <η (Laplace’s Equation) (7.1) • Bernoulli’s Equation (given some φ ): 2 ∂φ 1 pp− a ∂t +∇2 φ + ρ + gz = 0 for z <η (7.2) • No disturbance far away: ∂φ ∂t , ∇→φ 0 and p = pa − ρ gz (7.3) Finally we need to dictate the boundary conditions at the free surface, seafloor and on any body in the water: (1) Pressure is constant across the free surface interface: p = patm on z =η . ⎧∂φ 1 2 ⎫ p =−ρ ⎨ − V − gz⎬ + c ()t= patm . (7.4) ⎩ ∂t 2 ⎭ Choosing a suitable integration constant, ct( ) = patm , the boundary condition on z =η becomes ∂φ 1 ρ{ + V 2 + gη} = 0. -

PRESSURE 68 Kg 136 Kg Pressure: a Normal Force Exerted by a Fluid Per Unit Area
CLASS Second Unit PRESSURE 68 kg 136 kg Pressure: A normal force exerted by a fluid per unit area 2 Afeet=300cm 0.23 kgf/cm2 0.46 kgf/cm2 P=68/300=0.23 kgf/cm2 The normal stress (or “pressure”) on the feet of a chubby person is much greater than on the feet of a slim person. Some basic pressure 2 gages. • Absolute pressure: The actual pressure at a given position. It is measured relative to absolute vacuum (i.e., absolute zero pressure). • Gage pressure: The difference between the absolute pressure and the local atmospheric pressure. Most pressure-measuring devices are calibrated to read zero in the atmosphere, and so they indicate gage pressure. • Vacuum pressures: Pressures below atmospheric pressure. Throughout this text, the pressure P will denote absolute pressure unless specified otherwise. 3 Other Pressure Measurement Devices • Bourdon tube: Consists of a hollow metal tube bent like a hook whose end is closed and connected to a dial indicator needle. • Pressure transducers: Use various techniques to convert the pressure effect to an electrical effect such as a change in voltage, resistance, or capacitance. • Pressure transducers are smaller and faster, and they can be more sensitive, reliable, and precise than their mechanical counterparts. • Strain-gage pressure transducers: Work by having a diaphragm deflect between two chambers open to the pressure inputs. • Piezoelectric transducers: Also called solid- state pressure transducers, work on the principle that an electric potential is generated in a crystalline substance when it is subjected to mechanical pressure. Various types of Bourdon tubes used to measure pressure. -

On the Generation of Vorticity at a Free-Surface
Center for TurbulenceResearch Annual Research Briefs On the generation of vorticity at a freesurface By T Lundgren AND P Koumoutsakos Motivations and ob jectives In free surface ows there are many situations where vorticityenters a owin the form of a shear layer This o ccurs at regions of high surface curvature and sup ercially resembles separation of a b oundary layer at a solid b oundary corner but in the free surface ow there is very little b oundary layer vorticity upstream of the corner and the vorticity whichenters the owisentirely created at the corner Ro o d has asso ciated the ux of vorticityinto the ow with the deceleration ofalayer of uid near the surface These eects are quite clearly seen in spilling breaker ows studied by Duncan Philomin Lin Ro ckwell and Dabiri Gharib In this pap er we prop ose a description of free surface viscous ows in a vortex dynamics formulation In the vortex dynamics approach to uid dynamics the emphasis is on the vorticityvector which is treated as the primary variable the velo city is expressed as a functional of the vorticity through the BiotSavart integral In free surface viscous ows the surface app ears as a source or sink of vorticityand a suitable pro cedure is required to handle this as a vorticity b oundary condition As a conceptually attractivebypro duct of this study we nd that vorticityis conserved if one considers the vortex sheet at the free surface to contain surface vorticity Vorticity which uxes out of the uid and app ears to b e lost is really gained by the vortex sheet -

Pressure and Fluid Statics
cen72367_ch03.qxd 10/29/04 2:21 PM Page 65 CHAPTER PRESSURE AND 3 FLUID STATICS his chapter deals with forces applied by fluids at rest or in rigid-body motion. The fluid property responsible for those forces is pressure, OBJECTIVES Twhich is a normal force exerted by a fluid per unit area. We start this When you finish reading this chapter, you chapter with a detailed discussion of pressure, including absolute and gage should be able to pressures, the pressure at a point, the variation of pressure with depth in a I Determine the variation of gravitational field, the manometer, the barometer, and pressure measure- pressure in a fluid at rest ment devices. This is followed by a discussion of the hydrostatic forces I Calculate the forces exerted by a applied on submerged bodies with plane or curved surfaces. We then con- fluid at rest on plane or curved submerged surfaces sider the buoyant force applied by fluids on submerged or floating bodies, and discuss the stability of such bodies. Finally, we apply Newton’s second I Analyze the rigid-body motion of fluids in containers during linear law of motion to a body of fluid in motion that acts as a rigid body and ana- acceleration or rotation lyze the variation of pressure in fluids that undergo linear acceleration and in rotating containers. This chapter makes extensive use of force balances for bodies in static equilibrium, and it will be helpful if the relevant topics from statics are first reviewed. 65 cen72367_ch03.qxd 10/29/04 2:21 PM Page 66 66 FLUID MECHANICS 3–1 I PRESSURE Pressure is defined as a normal force exerted by a fluid per unit area. -

Boundary Conditions in Fluid Mechanics
Boundary Conditions in Fluid Mechanics R. Shankar Subramanian Department of Chemical and Biomolecular Engineering Clarkson University, Potsdam, New York 13699 The governing equations for the velocity and pressure fields are partial differential equations that are applicable at every point in a fluid that is being modeled as a continuum. When they are integrated in any given situation, we can expect to see arbitrary functions or constants appear in the solution. To evaluate these, we need additional statements about the velocity field and possibly its gradient at the natural boundaries of the flow domain. Such statements are known as boundary conditions. Usually, the specification of the pressure at one point in the system suffices to establish the pressure fields so that we shall only discuss boundary conditions on the velocity field here. For a more detailed discussion of various aspects, the reader is encouraged to consult either Leal (1) or Batchelor (2). Conditions at a rigid boundary It is convenient for the purpose of discussion to identify two types of boundaries. One is that at the interface between a fluid and a rigid surface. At such a surface, we shall require that the tangential component of the velocity of the fluid be the same as the tangential component of the velocity of the surface, and similarly the normal component of the velocity of the fluid be the same as the normal component of the velocity of the surface. The former is known as the “no slip” boundary condition, and has been found to be successful in describing most practical situations. It was a subject of controversy in the eighteenth and nineteenth centuries, and was finally accepted because predictions based on assuming it were found to be consistent with observations of macroscopic quantities such as the flow rate through a circular capillary under a given pressure drop. -
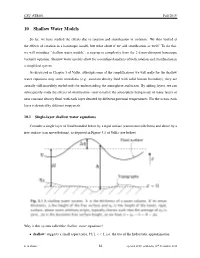
10 Shallow Water Models
CSU ATS601 Fall 2015 10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification as well? To do this, we will introduce “shallow water models”, a step-up in complexity from the 2-d non-divergent barotropic vorticity equation. Shallow water models allow for a combined analysis of both rotation and stratification in a simplified system. As discussed in Chapter 3 of Vallis, although some of the simplifications we will make for the shallow water equations may seem unrealistic (e.g. constant density fluid with solid bottom boundary), they are 5 Shallowactually still incredibly Water useful tools Models for understanding the atmosphere and ocean. By adding layers, we can So far wesubsequently have studied study the the effects eff ofects stratification due to - rotation and visualize (chapter the atmosphere 3) and being stratification made of many layers (chapter of 4) in isolation.near constant Shallow density water fluid,with models each layer allow denoted for a by combined different potential analysis temperatures. of both For eff theects ocean, in eacha highly simplifiedlayer system. is denoted They by different are very isopycnals. powerful in providing fundamental dynamical insight. 5.1 Introduction,10.1 Single-layer shallow Single water Layer equations[Vallis 3.1] Consider a single layer of fluid bounded below by a rigid surface and above by a free surface, Consider a single layer of fluid bounded below by a rigid surface (cannot move/deform) and above by a as depicted below (taken from Vallis, see figure caption for description of variables). -

Chapter 11 Flow with Free Surface
Chapter 11 Flow with Free Surface We have already encountered free surfaces in systems such as the drainage of a liquid along a wall. In this case the free surface was a material surface and the boundary condition was that of continuity of pressure and shear stress. The same boundary conditions would be used for wind-driven waves on water and the shape of the vortex formed when water drains from a bathtub. The dimensionless numbers of importance are the Reynolds number NULRe = ρ / μ , 2 2 ρ gL NRe Froude number NUgFr = / L, and gravity number NG ==. These μUNFr mentioned systems are of a macroscopic scale compared to surface forces and rheology and thus surface tension, surface elasticity, and surface viscosity were not significant. However, when the system dimensions become about 1 cm or less surface forces are no longer negligible and play an important role in the shape of the interface and in transport processes. The capillary number 2 NUCa = μ /σ and Bond number NgLBo = ρ /σ introduced in Chapter 6 become important dimensionless groups that quantify the ratio of viscous/capillary and gravity/capillary forces. As the dimensions decrease to about 1 mm we are in the range of capillary phenomena where surface tension and contact angles become important (e.g., the rise of a wetting liquid in a small capillary). As the dimensions decrease to 1 μm we are in the colloidal regime and not only is capillarity a dominant effect but also particles have spontaneous motion due to Brownian motion and thin films display optical interference as in the color of soap films.