Gravitational Lensing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Divinus Lux Observatory Bulletin: Report #28 100 Dave Arnold
Vol. 9 No. 2 April 1, 2013 Journal of Double Star Observations Page Journal of Double Star Observations VOLUME 9 NUMBER 2 April 1, 2013 Inside this issue: Using VizieR/Aladin to Measure Neglected Double Stars 75 Richard Harshaw BN Orionis (TYC 126-0781-1) Duplicity Discovery from an Asteroidal Occultation by (57) Mnemosyne 88 Tony George, Brad Timerson, John Brooks, Steve Conard, Joan Bixby Dunham, David W. Dunham, Robert Jones, Thomas R. Lipka, Wayne Thomas, Wayne H. Warren Jr., Rick Wasson, Jan Wisniewski Study of a New CPM Pair 2Mass 14515781-1619034 96 Israel Tejera Falcón Divinus Lux Observatory Bulletin: Report #28 100 Dave Arnold HJ 4217 - Now a Known Unknown 107 Graeme L. White and Roderick Letchford Double Star Measures Using the Video Drift Method - III 113 Richard L. Nugent, Ernest W. Iverson A New Common Proper Motion Double Star in Corvus 122 Abdul Ahad High Speed Astrometry of STF 2848 With a Luminera Camera and REDUC Software 124 Russell M. Genet TYC 6223-00442-1 Duplicity Discovery from Occultation by (52) Europa 130 Breno Loureiro Giacchini, Brad Timerson, Tony George, Scott Degenhardt, Dave Herald Visual and Photometric Measurements of a Selected Set of Double Stars 135 Nathan Johnson, Jake Shellenberger, Elise Sparks, Douglas Walker A Pixel Correlation Technique for Smaller Telescopes to Measure Doubles 142 E. O. Wiley Double Stars at the IAU GA 2012 153 Brian D. Mason Report on the Maui International Double Star Conference 158 Russell M. Genet International Association of Double Star Observers (IADSO) 170 Vol. 9 No. 2 April 1, 2013 Journal of Double Star Observations Page 75 Using VizieR/Aladin to Measure Neglected Double Stars Richard Harshaw Cave Creek, Arizona [email protected] Abstract: The VizierR service of the Centres de Donnes Astronomiques de Strasbourg (France) offers amateur astronomers a treasure trove of resources, including access to the most current version of the Washington Double Star Catalog (WDS) and links to tens of thousands of digitized sky survey plates via the Aladin Java applet. -
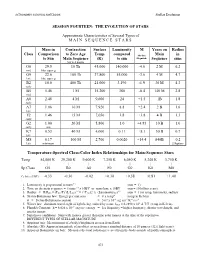
Temperature-Spectral Class-Color Index Relationships for Main
ASTRONOMY SURVIVAL NOTEBOOK Stellar Evolution SESSION FOURTEEN: THE EVOLUTION OF STARS Approximate Characteristics of Several Types of MAIN SEQUENCE STARS Mass in Contraction Surface Luminosity M Years on Radius Class Comparison to Zero Age Temp. compared Absolute Main in to Sun Main Sequence (K) to sun Magnitude Sequence suns Not well known O6 29.5 10 Th 45,000 140,000 -4.0 2 M 6.2 mid blue super g O9 22.6 100 Th 37,800 55,000 -3.6 4 M 4.7 late blue super g B2 10.0 400 Th 21,000 3,190 -1.9 30 M 4.3 early B5 5.46 1 M 15,200 380 -0.4 140 M 2.8 mid A0 2.48 4 M 9,600 24 +1.5 1B 1.8 early A7 1.86 10 M 7,920 8.8 +2.4 2 B 1.6 late F2 1.46 15 M 7,050 3.8 +3.8 4 B 1.3 early G2 1.00 20 M 5,800 1.0 +4.83 10 B 1.0 early sun K7 0.53 40 M 4,000 0.11 +8.1 50 B 0.7 late M8 0.17 100 M 2,700 0.0020 +14.4 840B 0.2 late minimum 2 Jupiters Temperature-Spectral Class-Color Index Relationships for Main-Sequence Stars Temp 54,000 K 29,200 K 9,600 K 7,350 K 6,050 K 5,240 K 3,750 K | | | | | | | Sp Class O5 B0 A0 F0 G0 K0 M0 Co Index (UBV) -0.33 -0.30 -0.02 +0.30 +0.58 +0.81 +1.40 1. -

The Gravitational Lens Effect of Galaxies and Black Holes
.f .(-L THE GRAVITATIONAL LENS EFFECT of GALAXIES and BLACK HOLES by Igor Bray, B.Sc. (Hons.) A thesis submitted in accordance with the requirements of the Degree of Doctor of Philosophy. Department of lr{athematical Physics The University of Adelaide South Australia January 1986 Awo.c(sd rt,zb to rny wife Ann CONTENTS STATEMENT ACKNOWLEDGEMENTS lt ABSTRACT lll PART I Spheroidal Gravitational Lenses I Introduction 1.1 Spherical gravitational lenses I 1.2 Spheroidal gravitational lenses 12 2 Derivationof I("o). ......16 3 Numerical Investigation 3.1 Evaluations oI l(zs) 27 3.2 Numericaltechniques 38 3.3 Numerical results 4L PART II Kerr Black llole As A Gravitational Lens 4 Introduction 4.1 Geodesics in the Kerr space-time 60 4.2 The equations of motion 64 5 Solving the Equations of Motion 5.1 Solution for 0 in the case m - a'= 0 68 5.2 Solution for / in the case m: a = O 76 5.3 Relating À and 7 to the position of the ìmage .. .. .82 5.4 Solution for 0 ... 89 5.5 Solution for / 104 5.6 Solution for ú. .. ..109 5.7 Quality of the approximations 115 6 Numerical investigation . .. ... tt7 References 122 STATEMENT This thesis contains no material which has been accepted for the award of any degree, and to the best of my knowledge and belief, contains no material previously published or written by another person except where due reference is made in the text. The author consents to the thesis being made available for photocopying and loan if applicable if accepted for the award of the degree. -

No Sign of Gravitational Lensing in the Cosmic Microwave Background
Perspectives No sign of gravitational lensing in the ., WFPC2, HST, NASA ., WFPC2, HST, cosmic microwave et al background Ron Samec ravitational lensing is a Ggravitational-optical effect whereby a background object like a distant quasar is magnified, distorted Andrew Fruchter (STScI) Image by and brightened by a foreground galaxy. It is alleged that the cluster of galaxies Abell 2218, distorts and magnifies It is one of the consequences of general light from galaxies behind it. relativity and is so well understood that fectly smooth black body spectrum of sioned by Hoyle and Wickramasinghe it now appears in standard optics text 5,6 books. Objects that are too far to be 2.725 K with very tiny fluctuations in and by Hartnett. They showed that seen are ‘focused’ by an intervening the pattern on the 70 μK level. These a homogeneous cloud mixture of car- concentration of matter and bought ‘bumps’ or patterns in the CMB are bon/silicate dust and iron or carbon into view to the earth based astronomer. supposedly the ‘seeds’ from which whiskers could produce such a back- One of the most interesting photos of the galaxies formed. Why is it so ground radiation. If the CMB is not the effects of gravitational lensing smooth? Alan Guth ‘solved’ this puz- of cosmological origin, all the ad hoc ideas that have been added to support is shown in the HST image of Abell zle by postulating that the universe was the big bang theory (like inflation) 2218 by Andrew Fruchter1 (Space originally a very tiny entity in thermal fall apart. -

A Gas Cloud on Its Way Towards the Super-Massive Black Hole in the Galactic Centre
1 A gas cloud on its way towards the super-massive black hole in the Galactic Centre 1 1,2 1 3 4 4,1 5 S.Gillessen , R.Genzel , T.K.Fritz , E.Quataert , C.Alig , A.Burkert , J.Cuadra , F.Eisenhauer1, O.Pfuhl1, K.Dodds-Eden1, C.F.Gammie6 & T.Ott1 1Max-Planck-Institut für extraterrestrische Physik (MPE), Giessenbachstr.1, D-85748 Garching, Germany ( [email protected], [email protected] ) 2Department of Physics, Le Conte Hall, University of California, 94720 Berkeley, USA 3Department of Astronomy, University of California, 94720 Berkeley, USA 4Universitätssternwarte der Ludwig-Maximilians-Universität, Scheinerstr. 1, D-81679 München, Germany 5Departamento de Astronomía y Astrofísica, Pontificia Universidad Católica de Chile, Vicuña Mackenna 4860, 7820436 Macul, Santiago, Chile 6Center for Theoretical Astrophysics, Astronomy and Physics Departments, University of Illinois at Urbana-Champaign, 1002 West Green St., Urbana, IL 61801, USA Measurements of stellar orbits1-3 provide compelling evidence4,5 that the compact radio source Sagittarius A* at the Galactic Centre is a black hole four million times the mass of the Sun. With the exception of modest X-ray and infrared flares6,7, Sgr A* is surprisingly faint, suggesting that the accretion rate and radiation efficiency near the event horizon are currently very low3,8. Here we report the presence of a dense gas cloud approximately three times the mass of Earth that is falling into the accretion zone of Sgr A*. Our observations tightly constrain the cloud’s orbit to be highly eccentric, with an innermost radius of approach of only ~3,100 times the event horizon that will be reached in 2013. -
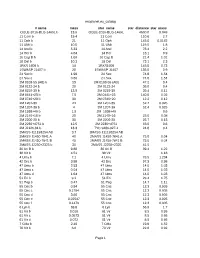
Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55 -

Vita Extraterrestre Sugli Esopianeti Nella Via Lattea
Vita extraterrestre sugli esopianeti nella Via Lattea Maria Cristina De Liso Liceo Cantonale di Locarno 2014-2015 Professori responsabili: Gianni Boffa e Christian Ferrari Indice 1 Premessa ...................................................................................................................................... 4 2 Introduzione ................................................................................................................................ 4 3 Origine dell’astronomia .............................................................................................................. 5 4 Verso il Sistema Solare e oltre ................................................................................................... 7 4.1 Il Sistema Solare .................................................................................................................. 8 4.2 Le leggi di Keplero ............................................................................................................ 10 4.3 Le comete ........................................................................................................................... 13 4.3.1 Origine ............................................................................................................................ 14 4.3.2 Classificazione e traiettoria orbitale ............................................................................ 15 4.3.3 Breve storia delle scoperte ............................................................................................ 16 -

Gravitational Lensing in a Black-Bounce Traversable Wormhole
Gravitational lensing in black-bounce spacetimes J. R. Nascimento,1, ∗ A. Yu. Petrov,1, y P. J. Porf´ırio,1, z and A. R. Soares1, x 1Departamento de F´ısica, Universidade Federal da Para´ıba, Caixa Postal 5008, 58051-970, Jo~aoPessoa, Para´ıba, Brazil In this work, we calculate the deflection angle of light in a spacetime that interpolates between regular black holes and traversable wormholes, depending on the free parameter of the metric. Afterwards, this angular deflection is substituted into the lens equations which allows to obtain physically measurable results, such as the position of the relativistic images and the magnifications. I. INTRODUCTION The angular deflection of light when passing through a gravitational field was one of the first predictions of the General Relativity (GR). Its confirmation played a role of a milestone for GR being one of the most important tests for it [1,2]. Then, gravitational lenses have become an important research tool in astrophysics and cosmology [3,4], allowing studies of the distribution of structures [5,6], dark matter [7] and some other topics [8{15]. Like as in the works cited earlier, the prediction made by Einstein was developed in the weak field approximation, that is, when the light ray passes at very large distance from the source which generates the gravitational lens. Under the phenomenological point of view, the recent discovery of gravitational waves by the LIGO-Virgo collaboration [16{18] opened up a new route of research, that is, to explore new cosmological observations by probing the Universe with gravitational waves, in particular, studying effects of gravitational lensing in the weak field approximation (see e.g. -

Gravitational Lensing and Optical Geometry • Marcus C
Gravitational Lensing and OpticalGravitational Geometry • Marcus C. Werner Gravitational Lensing and Optical Geometry A Centennial Perspective Edited by Marcus C. Werner Printed Edition of the Special Issue Published in Universe www.mdpi.com/journal/universe Gravitational Lensing and Optical Geometry Gravitational Lensing and Optical Geometry: A Centennial Perspective Editor Marcus C. Werner MDPI • Basel • Beijing • Wuhan • Barcelona • Belgrade • Manchester • Tokyo • Cluj • Tianjin Editor Marcus C. Werner Duke Kunshan University China Editorial Office MDPI St. Alban-Anlage 66 4052 Basel, Switzerland This is a reprint of articles from the Special Issue published online in the open access journal Universe (ISSN 2218-1997) (available at: https://www.mdpi.com/journal/universe/special issues/ gravitational lensing optical geometry). For citation purposes, cite each article independently as indicated on the article page online and as indicated below: LastName, A.A.; LastName, B.B.; LastName, C.C. Article Title. Journal Name Year, Article Number, Page Range. ISBN 978-3-03943-286-8 (Hbk) ISBN 978-3-03943-287-5 (PDF) c 2020 by the authors. Articles in this book are Open Access and distributed under the Creative Commons Attribution (CC BY) license, which allows users to download, copy and build upon published articles, as long as the author and publisher are properly credited, which ensures maximum dissemination and a wider impact of our publications. The book as a whole is distributed by MDPI under the terms and conditions of the Creative Commons license CC BY-NC-ND. Contents About the Editor .............................................. vii Preface to ”Gravitational Lensing and Optical Geometry: A Centennial Perspective” ..... ix Amir B. -

Terrestrial Planets in High-Mass Disks Without Gas Giants
A&A 557, A42 (2013) Astronomy DOI: 10.1051/0004-6361/201321304 & c ESO 2013 Astrophysics Terrestrial planets in high-mass disks without gas giants G. C. de Elía, O. M. Guilera, and A. Brunini Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata and Instituto de Astrofísica de La Plata, CCT La Plata-CONICET-UNLP, Paseo del Bosque S/N, 1900 La Plata, Argentina e-mail: [email protected] Received 15 February 2013 / Accepted 24 May 2013 ABSTRACT Context. Observational and theoretical studies suggest that planetary systems consisting only of rocky planets are probably the most common in the Universe. Aims. We study the potential habitability of planets formed in high-mass disks without gas giants around solar-type stars. These systems are interesting because they are likely to harbor super-Earths or Neptune-mass planets on wide orbits, which one should be able to detect with the microlensing technique. Methods. First, a semi-analytical model was used to define the mass of the protoplanetary disks that produce Earth-like planets, super- Earths, or mini-Neptunes, but not gas giants. Using mean values for the parameters that describe a disk and its evolution, we infer that disks with masses lower than 0.15 M are unable to form gas giants. Then, that semi-analytical model was used to describe the evolution of embryos and planetesimals during the gaseous phase for a given disk. Thus, initial conditions were obtained to perform N-body simulations of planetary accretion. We studied disks of 0.1, 0.125, and 0.15 M. -

Mètodes De Detecció I Anàlisi D'exoplanetes
MÈTODES DE DETECCIÓ I ANÀLISI D’EXOPLANETES Rubén Soussé Villa 2n de Batxillerat Tutora: Dolors Romero IES XXV Olimpíada 13/1/2011 Mètodes de detecció i anàlisi d’exoplanetes . Índex - Introducció ............................................................................................. 5 [ Marc Teòric ] 1. L’Univers ............................................................................................... 6 1.1 Les estrelles .................................................................................. 6 1.1.1 Vida de les estrelles .............................................................. 7 1.1.2 Classes espectrals .................................................................9 1.1.3 Magnitud ........................................................................... 9 1.2 Sistemes planetaris: El Sistema Solar .............................................. 10 1.2.1 Formació ......................................................................... 11 1.2.2 Planetes .......................................................................... 13 2. Planetes extrasolars ............................................................................ 19 2.1 Denominació .............................................................................. 19 2.2 Història dels exoplanetes .............................................................. 20 2.3 Mètodes per detectar-los i saber-ne les característiques ..................... 26 2.3.1 Oscil·lació Doppler ........................................................... 27 2.3.2 Trànsits -

En Interaktiv Visualisering Av Data Och Upptäcktsmetoder Karin Reidarman
LIU-ITN-TEK-A-018/045--SE Exoplaneter: En Interaktiv Visualisering av Data och Upptäcktsmetoder Karin Reidarman 2018-11-30 Department of Science and Technology Institutionen för teknik och naturvetenskap Linköping University Linköpings universitet nedewS ,gnipökrroN 47 106-ES 47 ,gnipökrroN nedewS 106 47 gnipökrroN LIU-ITN-TEK-A-018/045--SE Exoplaneter: En Interaktiv Visualisering av Data och Upptäcktsmetoder Examensarbete utfört i Medieteknik vid Tekniska högskolan vid Linköpings universitet Karin Reidarman Handledare Emil Axelsson Examinator Anders Ynnerman Norrköping 2018-11-30 Upphovsrätt Detta dokument hålls tillgängligt på Internet – eller dess framtida ersättare – under en längre tid från publiceringsdatum under förutsättning att inga extra- ordinära omständigheter uppstår. Tillgång till dokumentet innebär tillstånd för var och en att läsa, ladda ner, skriva ut enstaka kopior för enskilt bruk och att använda det oförändrat för ickekommersiell forskning och för undervisning. Överföring av upphovsrätten vid en senare tidpunkt kan inte upphäva detta tillstånd. All annan användning av dokumentet kräver upphovsmannens medgivande. För att garantera äktheten, säkerheten och tillgängligheten finns det lösningar av teknisk och administrativ art. Upphovsmannens ideella rätt innefattar rätt att bli nämnd som upphovsman i den omfattning som god sed kräver vid användning av dokumentet på ovan beskrivna sätt samt skydd mot att dokumentet ändras eller presenteras i sådan form eller i sådant sammanhang som är kränkande för upphovsmannens litterära eller konstnärliga anseende eller egenart. För ytterligare information om Linköping University Electronic Press se förlagets hemsida http://www.ep.liu.se/ Copyright The publishers will keep this document online on the Internet - or its possible replacement - for a considerable time from the date of publication barring exceptional circumstances.