Modern Theory and Practice of Tide Analysis and Tidal Power
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Science Grades 3-4. New York City Board of Education, Brooklyn, N.Y
DOCUMFNT RESUM1 E ED 023 603 SE 005 416 Science Grades 3-4. New York City Board of Education, Brooklyn, N.Y. Bureauof Curriculum Development. Pub Date 66 Note -353p. Street, Brooklyn, Avatlable from-New York City Board of Education, PublicationsSales Office, 110 Livingston New York 11201 ($250). EDRS Price MF -$150 HC Not Available from EDRS. Descriptors-Biology, *Curriculum, Earth Science, 'ElementarySchool Science, *General Science,Grade 3, Grade 4, Instructional Materials, Physical Sciences, ScienceActivities, *Teaching Guides Identifiers -Board of Education, New York, New YorkCity This handbook provides the elementaryschool teacher with specificsuggestions regarding use of materials and organizationof effective learning experiencesin science at th;*3 level. The book containsthree sections:An introductionemphasizes both science knowledge and processwhile the other two sectionsdeal with subject matter topics for grades 3 and 4.Suggestions for eva!uation followeach science topic.A bibliography of both children's books andprofessiona books for scienceteaching in the elementary school is provided.An extensive filmlistis also developed.Topics developed in grade 3 include electricity,the earth and the sun, needsof plants and animals, sound, weather, friction, gravity,motion, and rocks. Topicsdeveloped in grade 4 include using a compass, the moon,plants, sound, weather, movingthings, and water. (BC) IN SCIENCE Grades 3-4 o o , , jy ;f. 4t, ,r ' r " . e ".4.A of; , o * , 11 4 A: 4it ;0: ,?; \\ me*. "ag 44; ,* =ttrz't " ilas beengrantAi P>rmission toreproduce thisc.,tmtrir71,1erl work Informeon Center(ERIC) and ttli -.3) theEducaVonal Resources operating under contractwith the U.S. Officeor thm organization the ERIC systern EtIwation to reproducedocuments included in of microficheonly, but this rightIs not corferred tO SIN means from the ERICDocument "Ie.,. -

Quantitative Composition and Granulometry of Aeolian Bedforms in Endeavour and Gale Craters Inferred from Visible Near-Infrared Spectra
45th Lunar and Planetary Science Conference (2014) 1431.pdf QUANTITATIVE COMPOSITION AND GRANULOMETRY OF AEOLIAN BEDFORMS IN ENDEAVOUR AND GALE CRATERS INFERRED FROM VISIBLE NEAR-INFRARED SPECTRA. Mathieu G.A. Lapotre1, Bethany L. Ehlmann1,2, Raymond E. Arvidson3. 1Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA, USA. 2Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, USA, 3Department of Earth & Planetary Sciences, Washington University in St. Louis, MO, USA. Introduction: Modern Mars is a wind world. Its ing Spectrometer for Mars (CRISM) visible near- surface hosts a variety of aeolian features, such as line- infrared spectra (VISIR). The goal of this study is to ar, barchan and star dunes, ripples, granule ripples, compare inversions made from orbit to ground truth yardangs and ventifacts [1]. Even though active sand provided by instruments aboard Opportunity at En- transport was observed at the surface [2], it is not clear deavour Crater, Terra Meridiani and Curiosity in Gale whether all of the preserved aeolian bedforms are ac- crater. tive. In particular, transverse aeolian ridges have been We use Hapke’s bidirectional reflectance spectros- suggested to be remnant dunes that formed under past copy theory [6] to invert for optical constants of miner- climatic conditions [3]. als from laboratory spectra [e.g., 7, 8]. These are used Sand transport is largely controlled by the size and to compute single scattering albedos of mineral the density of the grains [4]. Moreover, dunes and rip- endmember components of varying grain sizes. We use ples form in unimodally distributed sand particles from an atmospheric radiative transfer approach, DISORT different instabilities, and the wavelengths of these [9], to correct the CRISM spectra for the effects of the different bedforms do not have the same dependence Martian atmosphere. -

Aphelion) 25/02/04 16:20 Page 1
SORTIE (Aphelion) 25/02/04 16:20 Page 1 Aphelion™ IMAGE PROCESSING AND IMAGE ANALYSIS SOFTWARE TO FACE NEW CHALLENGES ORGANIZATIONS ALREADY USING APHELION™ 3M (USA) Halliburton (USA) Procter & Gamble (USA & Europe) Arcelor (Europe) Hewlett-Packard (UK) Queen’s College (UK) Boeing Aerospace (USA) Hitachi (Japan) Rolls Royce (UK) CEA (France) Hoya (Japan) SNECMA Moteurs (France) CNRS (France) Joint Research Center (Europe) Thales (France) CSIRO (Australia) Kawasaki Heavy Industry (Japan) Toshiba (Japan) Corning (France) Kodak Industrie (France) Université de Lausanne (Switzerland) Dako (USA) Lilly (USA) Université de Liège (Belgium) Dornier (Germany) Lockheed Martin (USA) University of Massachusetts (USA) EADS (France) Mitsubishi (Japan) Unilever (UK) Ecole de Technologie Supérieure (Canada) Nikon (Japan) US Navy (USA) FedEx (USA) Nissan (Japan) Volvo Aero Corporation (Sweden) FAO, Defence Research Establishment (Sweden) Pechiney (France) Xerox (USA) Ford (USA) Peugeot-Citroën (France) Framatome (France) Philips (France) Aphelion IMAGE PROCESSING IMAGE PROCESSING AND IMAGE ANALYSIS SOFTWARE TO FACE NEW CHALLENGE AND IMAGE ANALYSIS SOFTWARE TO FACE NEW CHALLENGES PRODUCT DISTRIBUTION Licensing: Single-user license & site license for end-users Run-time licenses for OEMs Downloadable from web Standard package: APHELION™ Developer includes all the standard libraries available as DLLs & ActiveX components, development capabilities, and the graphical user interface BIOLOGY / COSMETICS / GEOLOGY INSPECTION / MATERIALS SCIENCE Optional modules: 3D Image Processing METROLOGY 3D Image Display OBJECT RECOGNITION Recognition Toolkit VisionTutor, a computer vision course including extensive exercises PHARMACOLOGY / QUALITY CONTROL / REMOTE SENSING / ROBOTICS Interface to a wide variety of frame grabber boards SECURITY / TRACKING Twain interface to control scanners and digital cameras Video media interface Interface to control microscope stages ActiveX components: Extensive Image Processing libraries for automated applications. -

Atmospheric Tidal Waves in the Troposphere and Lower Stratosphere Observed by Wuhan MST Radar
2nd URSI AT-RASC, Gran Canaria, 28 May – 1 June 2018 Atmospheric tidal waves in the troposphere and lower stratosphere observed by Wuhan MST radar Haiyin Qing School of Physics and Electronic Engineering, Leshan Normal University, 614000, China Abstract 2. Data and Method In this paper, the observation data of the Wuhan MST radar in the whole 2012 are used making a statistical analysis on This paper mainly deals with the observation data of the low stratospheric and troposphere tidal waves. The Wuhan MST radar in 2012. The months of 12, 1, 2 are results show that: (1) the diurnal tide is the strongest and divided into winter; the months of 3, 4, 5 are divided into most of the time at low levels of Sunday tide is stronger spring; the months of 6, 7, 8 are divided into summer; and than the high tide of Sunday. (2) the amplitude of the tidal the months of 9,10,11 are divided into autumn. Then wave is not modulated by the fluctuation with a smaller choose the most complete data in the strength of 50 days to time scale than their periods, and only these waves with a carry out different tidal wave components in the four longer time scale than their periods can affect the variation seasons. The time resolution of the data is 0.5 h, and the of the amplitude of the tidal waves. slip time length is 4 days. Fitting time series of wind field data in time window by least square method, the fitting Keywords: MST radar; Atmospheric tidal waves; model is as follows: troposphere; stratosphere; planetary waves (1) 2 () =0+( +) 1. -

Study of Earth's Gravity Tide and Ocean Loading
CHINESE JOURNAL OF GEOPHYSICS Vol.49, No.3, 2006, pp: 657∼670 STUDY OF EARTH’S GRAVITY TIDE AND OCEAN LOADING CHARACTERISTICS IN HONGKONG AREA SUN He-Ping1 HSU House1 CHEN Wu2 CHEN Xiao-Dong1 ZHOU Jiang-Cun1 LIU Ming1 GAO Shan2 1 Key Laboratory of Dynamical Geodesy, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China 2 Department of Land Surveying and Geoinformatics, Hong-Kong Polytechnic University, Hung Hom, Knowloon, Hong Kong Abstract The tidal gravity observation achievements obtained in Hongkong area are introduced, the first complete tidal gravity experimental model in this area is obtained. The ocean loading characteristics are studied systematically by using global and local ocean models as well as tidal gauge data, the suitability of global ocean models is also studied. The numerical results show that the ocean models in diurnal band are more stable than those in semidiurnal band, and the correction of the change in tidal height plays a significant role in determining accurately the phase lag of the tidal gravity. The gravity observation residuals and station background noise level are also investigated. The study fills the empty of the tidal gravity observation in Crustal Movement Observation Network of China and can provide the effective reference and service to ground surface and space geodesy. Key words Hongkong area, Tidal gravity, Experimental model, Ocean loading 1 INTRODUCTION The Earth’s gravity is a science studying the temporal and spatial distribution of the gravity field and its physical mechanism. Generally, its achievements can be used in many important domains such as space science, geophysics, geodesy, oceanography, and so on. -

Chapter 5 Water Levels and Flow
253 CHAPTER 5 WATER LEVELS AND FLOW 1. INTRODUCTION The purpose of this chapter is to provide the hydrographer and technical reader the fundamental information required to understand and apply water levels, derived water level products and datums, and water currents to carry out field operations in support of hydrographic surveying and mapping activities. The hydrographer is concerned not only with the elevation of the sea surface, which is affected significantly by tides, but also with the elevation of lake and river surfaces, where tidal phenomena may have little effect. The term ‘tide’ is traditionally accepted and widely used by hydrographers in connection with the instrumentation used to measure the elevation of the water surface, though the term ‘water level’ would be more technically correct. The term ‘current’ similarly is accepted in many areas in connection with tidal currents; however water currents are greatly affected by much more than the tide producing forces. The term ‘flow’ is often used instead of currents. Tidal forces play such a significant role in completing most hydrographic surveys that tide producing forces and fundamental tidal variations are only described in general with appropriate technical references in this chapter. It is important for the hydrographer to understand why tide, water level and water current characteristics vary both over time and spatially so that they are taken fully into account for survey planning and operations which will lead to successful production of accurate surveys and charts. Because procedures and approaches to measuring and applying water levels, tides and currents vary depending upon the country, this chapter covers general principles using documented examples as appropriate for illustration. -

Tidal Wind Oscillations in the Tropical Lower Atmosphere As Observed by Indian MST Radar
Annales Geophysicae (2001) 19: 991–999 c European Geophysical Society 2001 Annales Geophysicae Tidal wind oscillations in the tropical lower atmosphere as observed by Indian MST Radar M. N. Sasi, G. Ramkumar, and V. Deepa Space Physics Laboratory Vikram Sarabhai Space Centre, Trivandrum 695 022, India Received: 7 November 2000 – Revised: 17 May 2001 – Accepted: 18 May 2001 Abstract. Diurnal tidal components in horizontal winds marised the salient features of the classical theory of tides measured by MST radar in the troposphere and lower strato- under various simplifying assumptions, such as motionless sphere over a tropical station Gadanki (13.5◦ N, 79.2◦ E) are atmosphere, zonal symmetry of the heat sources, etc. and presented for the autumn equinox, winter, vernal equinox and this classical theory is successful in explaining the major summer seasons. For this purpose radar data obtained over features of tidal oscillations in the upper atmosphere. How- many diurnal cycles from September 1995 to August 1996 ever, if the water vapour and ozone distribution have zonal are used. The results obtained show that although the sea- asymmetry, solar thermal excitation of these constituents will sonal variation of the diurnal tidal amplitudes in zonal and generate tidal modes with zonal wave numbers not equal to meridional winds is not strong, vertical phase propagation 1. This means that solar thermal excitation will not be able characteristics show significant seasonal variation. An at- to follow the apparent westward motion of the Sun. These tempt is made to simulate the diurnal tidal amplitudes and Sun-asynchronous tidal modes are known as nonmigrating phases in the lower atmosphere over Gadanki using classical modes. -
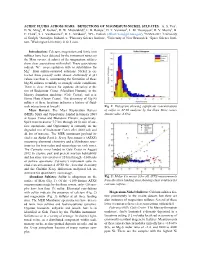
Acidic Fluids Across Mars: Detections of Magnesium-Nickel Sulfates
ACIDIC FLUIDS ACROSS MARS: DETECTIONS OF MAGNESIUM-NICKEL SULFATES. A. S. Yen1, D. W. Ming2, R. Gellert3, D. W. Mittlefehldt2, E. B. Rampe4, D. T. Vaniman5, L. M. Thompson6, R. V. Morris2, B. C. Clark7, S. J. VanBommel3, R. E. Arvidson8, 1JPL- Caltech ([email protected]), 2NASA-JSC, 3University of Guelph, 4Aerodyne Industries, 5Planetary Science Institute, 6University of New Brunswick, 7Space Science Insti- tute, 7Washington University in St. Louis. Introduction: Calcium, magnesium and ferric iron sulfates have been detected by the instrument suites on the Mars rovers. A subset of the magnesium sulfates show clear associations with nickel. These associations indicate Ni2+ co-precipitation with or substitution for Mg2+ from sulfate-saturated solutions. Nickel is ex- tracted from primary rocks almost exclusively at pH values less than 6, constraining the formation of these Mg-Ni sulfates to mildly to strongly acidic conditions. There is clear evidence for aqueous alteration at the rim of Endeavour Crater (Meridiani Planum), in the Murray formation mudstone (Gale Crater), and near Home Plate (Gusev Crater). The discovery of Mg-Ni sulfates at these locations indicates a history of fluid- rock interactions at low pH. Fig 1: Histogram showing significant concentrations Mars Rovers: The Mars Exploration Rovers of sulfur in APXS analyses by the three Mars rovers (MER), Spirit and Opportunity, landed in January 2004 (mean value: 6.6%). at Gusev Crater and Meridiani Planum, respectively. Spirit traversed over 7.7 km through 2210 sols of sur- face operations, and Opportunity is currently on the degraded rim of Endeavour Crater after 4600 sols and 44 km of traverse. -

A Journey of Exploration to the Polar Regions of a Star: Probing the Solar
Experimental Astronomy manuscript No. (will be inserted by the editor) A journey of exploration to the polar regions of a star: probing the solar poles and the heliosphere from high helio-latitude Louise Harra · Vincenzo Andretta · Thierry Appourchaux · Fr´ed´eric Baudin · Luis Bellot-Rubio · Aaron C. Birch · Patrick Boumier · Robert H. Cameron · Matts Carlsson · Thierry Corbard · Jackie Davies · Andrew Fazakerley · Silvano Fineschi · Wolfgang Finsterle · Laurent Gizon · Richard Harrison · Donald M. Hassler · John Leibacher · Paulett Liewer · Malcolm Macdonald · Milan Maksimovic · Neil Murphy · Giampiero Naletto · Giuseppina Nigro · Christopher Owen · Valent´ın Mart´ınez-Pillet · Pierre Rochus · Marco Romoli · Takashi Sekii · Daniele Spadaro · Astrid Veronig · W. Schmutz Received: date / Accepted: date L. Harra PMOD/WRC, Dorfstrasse 33, CH-7260 Davos Dorf and ETH-Z¨urich, Z¨urich, Switzerland E-mail: [email protected]; ORCID: 0000-0001-9457-6200 V. Andretta INAF, Osservatorio Astronomico di Capodimonte, Naples, Italy E-mail: vin- [email protected]; ORCID: 0000-0003-1962-9741 T. Appourchaux Institut d’Astrophysique Spatiale, CNRS, Universit´e Paris–Saclay, France; E-mail: [email protected]; ORCID: 0000-0002-1790-1951 F. Baudin Institut d’Astrophysique Spatiale, CNRS, Universit´e Paris–Saclay, France; E-mail: [email protected]; ORCID: 0000-0001-6213-6382 L. Bellot Rubio Inst. de Astrofisica de Andaluc´ıa, Granada Spain A.C. Birch Max-Planck-Institut f¨ur Sonnensystemforschung, 37077 G¨ottingen, Germany; E-mail: arXiv:2104.10876v1 [astro-ph.SR] 22 Apr 2021 [email protected]; ORCID: 0000-0001-6612-3861 P. Boumier Institut d’Astrophysique Spatiale, CNRS, Universit´e Paris–Saclay, France; E-mail: 2 Louise Harra et al. -

Up, Up, and Away by James J
www.astrosociety.org/uitc No. 34 - Spring 1996 © 1996, Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, CA 94112. Up, Up, and Away by James J. Secosky, Bloomfield Central School and George Musser, Astronomical Society of the Pacific Want to take a tour of space? Then just flip around the channels on cable TV. Weather Channel forecasts, CNN newscasts, ESPN sportscasts: They all depend on satellites in Earth orbit. Or call your friends on Mauritius, Madagascar, or Maui: A satellite will relay your voice. Worried about the ozone hole over Antarctica or mass graves in Bosnia? Orbital outposts are keeping watch. The challenge these days is finding something that doesn't involve satellites in one way or other. And satellites are just one perk of the Space Age. Farther afield, robotic space probes have examined all the planets except Pluto, leading to a revolution in the Earth sciences -- from studies of plate tectonics to models of global warming -- now that scientists can compare our world to its planetary siblings. Over 300 people from 26 countries have gone into space, including the 24 astronauts who went on or near the Moon. Who knows how many will go in the next hundred years? In short, space travel has become a part of our lives. But what goes on behind the scenes? It turns out that satellites and spaceships depend on some of the most basic concepts of physics. So space travel isn't just fun to think about; it is a firm grounding in many of the principles that govern our world and our universe. -

Surface Gravity and Interstellar Settlement (Version 3.0 September 2016)
Surface Gravity and Interstellar Settlement (version 3.0 September 2016) by Gerald D. Nordley 1238 Prescott Avenue Sunnyvale, CA 94089-2334 [email protected] Abstract. Gravity determines the scale of many physical Jupiter's inner satellites melts the ice of Europa and drives phenomena on and above a world's surface. Assuming that tool- volcanoes on Io, and that Mars in the past has had rain and using intelligences come from, and would settle, worlds with solid floods serves notice that worlds that are significantly less surfaces and gravities equal or less than that of their origin, we massive than Earth and have significantly less surface gravity note that such worlds in the Solar System have surface gravities can still have the deep atmospheres and liquid water significantly lower than that of Earth. The distribution of these temperatures needed to sustain life. surface gravities clumps around factors of about 2.5 and favors worlds with about one-sixth Earth gravity, conventionally 2. Surface Gravity Basics considered too small to retain atmospheres. Titan, however, Mass is, roughly, a measure of the amount of substance. shows that low surface gravity does not, in itself, preclude the Weight is the force by which that substance is attracted to presence a substantial atmosphere. Where small worlds have another mass. This force is directly proportional to the product of low exobase temperatures,and protection from stellar winds, both masses and inversely proportional to the square of the substantial atmospheres may be retained. distance between them. A spherically symmetric planet can be Significantly lower surface gravity affects a number of physical treated as if all the mass were at the center, so the relevant phenomena that affect environment and technological evolution-- distance is the radius from the center to the object. -

What to Expect When You're Expecting: a Tsunami
WHAT TO EXPECT WHEN YOU’RE EXPECTING Tsunami Hazards in Washington State Maximilian Dixon – Washington Emergency Management Division Geological Hazards in Washington WA has the 2nd highest earthquake risk in the US We also have… • Tsunamis - local and distant M9 recurrence 300-600 years • 5 active volcanoes M7 recurrence 30-50 years • Landslides Cascadia Subduction Zone • 700 miles long (1,130 km) • Breaks 300 – 600 years (~500 years on average) • Last great rupture in 1700 (320 years ago) • 10-20% chance within next 50 years Juan North • Magnitude 8.0-9.0+ de America • Shaking felt region-wide for 3–6 minutes plate • Shaking intensity is greatest along coast & Fuca where local conditions amplify seismic waves plate • Earthquake followed by a major tsunami hitting WA’s outer coast in 15-20 min • Many large aftershocks will follow main quake Distant vs Local Tsunamis Distant Local • No earthquake felt • Event will typically be felt • > 3 hours until first wave arrives • < 3 hours until first wave arrives • Warning must be distributed • Earthquake is primary warning • Less inundation/slower currents • More inundation/faster currents • Less severe impact to coast • Significant impact to coast Local Tsunamis THE SHAKING IS YOUR WARNING! The first waves arrive within seconds to minutes Devils Mountain Fault South Whidbey Island Fault Cascadia Seattle Fault Subduction Zone Tacoma Fault Know the Natural Tsunami Warning Signs 1. Feel a long or strong ground shaking at the coast 2. See a sudden rise or fall of the ocean 3. Hear a loud roaring sound