Physical Mechanisms of Control of Gliding in Flying Snakes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ONEP V09.Pdf
Compiled by Jarujin Nabhitabhata Tanya Chan-ard Yodchaiy Chuaynkern OEPP BIODIVERSITY SERIES volume nine OFFICE OF ENVIRONMENTAL POLICY AND PLANNING MINISTRY OF SCIENCE TECHNOLOGY AND ENVIRONMENT 60/1 SOI PIBULWATTANA VII, RAMA VI RD., BANGKOK 10400 THAILAND TEL. (662) 2797180, 2714232, 2797186-9 FAX. (662) 2713226 Office of Environmental Policy and Planning 2000 NOT FOR SALE NOT FOR SALE NOT FOR SALE Compiled by Jarujin Nabhitabhata Tanya Chan-ard Yodchaiy Chuaynkern Office of Environmental Policy and Planning 2000 First published : September 2000 by Office of Environmental Policy and Planning (OEPP), Thailand. ISBN : 974–87704–3–5 This publication is financially supported by OEPP and may be reproduced in whole or in part and in any form for educational or non–profit purposes without special permission from OEPP, providing that acknowledgment of the source is made. No use of this publication may be made for resale or for any other commercial purposes. Citation : Nabhitabhata J., Chan ard T., Chuaynkern Y. 2000. Checklist of Amphibians and Reptiles in Thailand. Office of Environmental Policy and Planning, Bangkok, Thailand. Authors : Jarujin Nabhitabhata Tanya Chan–ard Yodchaiy Chuaynkern National Science Museum Available from : Biological Resources Section Natural Resources and Environmental Management Division Office of Environmental Policy and Planning Ministry of Science Technology and Environment 60/1 Rama VI Rd. Bangkok 10400 THAILAND Tel. (662) 271–3251, 279–7180, 271–4232–8 279–7186–9 ext 226, 227 Facsimile (662) 279–8088, 271–3251 Designed & Printed :Integrated Promotion Technology Co., Ltd. Tel. (662) 585–2076, 586–0837, 913–7761–2 Facsimile (662) 913–7763 2 1. -

WHO Guidance on Management of Snakebites
GUIDELINES FOR THE MANAGEMENT OF SNAKEBITES 2nd Edition GUIDELINES FOR THE MANAGEMENT OF SNAKEBITES 2nd Edition 1. 2. 3. 4. ISBN 978-92-9022- © World Health Organization 2016 2nd Edition All rights reserved. Requests for publications, or for permission to reproduce or translate WHO publications, whether for sale or for noncommercial distribution, can be obtained from Publishing and Sales, World Health Organization, Regional Office for South-East Asia, Indraprastha Estate, Mahatma Gandhi Marg, New Delhi-110 002, India (fax: +91-11-23370197; e-mail: publications@ searo.who.int). The designations employed and the presentation of the material in this publication do not imply the expression of any opinion whatsoever on the part of the World Health Organization concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. Dotted lines on maps represent approximate border lines for which there may not yet be full agreement. The mention of specific companies or of certain manufacturers’ products does not imply that they are endorsed or recommended by the World Health Organization in preference to others of a similar nature that are not mentioned. Errors and omissions excepted, the names of proprietary products are distinguished by initial capital letters. All reasonable precautions have been taken by the World Health Organization to verify the information contained in this publication. However, the published material is being distributed without warranty of any kind, either expressed or implied. The responsibility for the interpretation and use of the material lies with the reader. In no event shall the World Health Organization be liable for damages arising from its use. -

Snakes of South-East Asia Including Myanmar, Thailand, Malaysia, Singapore, Sumatra, Borneo, Java and Bali
A Naturalist’s Guide to the SNAKES OF SOUTH-EAST ASIA including Myanmar, Thailand, Malaysia, Singapore, Sumatra, Borneo, Java and Bali Indraneil Das First published in the United Kingdom in 2012 by Beaufoy Books n n 11 Blenheim Court, 316 Woodstock Road, Oxford OX2 7NS, England Contents www.johnbeaufoy.com 10 9 8 7 6 5 4 3 2 1 Introduction 4 Copyright © 2012 John Beaufoy Publishing Limited Copyright in text © Indraneil Das Snake Topography 4 Copyright in photographs © [to come] Dealing with Snake Bites 6 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of the publishers. About this Book 7 ISBN [to come] Glossary 8 Edited, designed and typeset by D & N Publishing, Baydon, Wiltshire, UK Printed and bound [to come] Species Accounts and Photographs 11 Checklist of South-East Asian Snakes 141 Dedication Nothing would have happened without the support of the folks at home: my wife, Genevieve V.A. Gee, and son, Rahul Das. To them, I dedicate this book. Further Reading 154 Acknowledgements 155 Index 157 Edited and designed by D & N Publishing, Baydon, Wiltshire, UK Printed and bound in Malaysia by Times Offset (M) Sdn. Bhd. n Introduction n n Snake Topography n INTRODUCTION Snakes form one of the major components of vertebrate fauna of South-East Asia. They feature prominently in folklore, mythology and other belief systems of the indigenous people of the region, and are of ecological and conservation value, some species supporting significant (albeit often illegal) economic activities (primarily, the snake-skin trade, but also sale of meat and other body parts that purportedly have medicinal properties). -

Download Download
HAMADRYAD Vol. 27. No. 2. August, 2003 Date of issue: 31 August, 2003 ISSN 0972-205X CONTENTS T. -M. LEONG,L.L.GRISMER &MUMPUNI. Preliminary checklists of the herpetofauna of the Anambas and Natuna Islands (South China Sea) ..................................................165–174 T.-M. LEONG & C-F. LIM. The tadpole of Rana miopus Boulenger, 1918 from Peninsular Malaysia ...............175–178 N. D. RATHNAYAKE,N.D.HERATH,K.K.HEWAMATHES &S.JAYALATH. The thermal behaviour, diurnal activity pattern and body temperature of Varanus salvator in central Sri Lanka .........................179–184 B. TRIPATHY,B.PANDAV &R.C.PANIGRAHY. Hatching success and orientation in Lepidochelys olivacea (Eschscholtz, 1829) at Rushikulya Rookery, Orissa, India ......................................185–192 L. QUYET &T.ZIEGLER. First record of the Chinese crocodile lizard from outside of China: report on a population of Shinisaurus crocodilurus Ahl, 1930 from north-eastern Vietnam ..................193–199 O. S. G. PAUWELS,V.MAMONEKENE,P.DUMONT,W.R.BRANCH,M.BURGER &S.LAVOUÉ. Diet records for Crocodylus cataphractus (Reptilia: Crocodylidae) at Lake Divangui, Ogooué-Maritime Province, south-western Gabon......................................................200–204 A. M. BAUER. On the status of the name Oligodon taeniolatus (Jerdon, 1853) and its long-ignored senior synonym and secondary homonym, Oligodon taeniolatus (Daudin, 1803) ........................205–213 W. P. MCCORD,O.S.G.PAUWELS,R.BOUR,F.CHÉROT,J.IVERSON,P.C.H.PRITCHARD,K.THIRAKHUPT, W. KITIMASAK &T.BUNDHITWONGRUT. Chitra burmanica sensu Jaruthanin, 2002 (Testudines: Trionychidae): an unavailable name ............................................................214–216 V. GIRI,A.M.BAUER &N.CHATURVEDI. Notes on the distribution, natural history and variation of Hemidactylus giganteus Stoliczka, 1871 ................................................217–221 V. WALLACH. -

SR 55(4) 42-44.Pdf
FEATURE ARTICLE Oriental fl ying gurnard (Dactyloptera orientalis) Carribean fl ying gurnard (Dactyloptera volitans) Fliers Without Prafulla Kumar Mohanty Four-winged fl ying fi sh Feathers & Damayanti Nayak (Cypselurus californicus) LIGHT is an amazing 2. Flying squid: In the Flying squid accomplishment that evolved (Todarodes pacifi cus), commonly Ffi rst in the insects and was called Japanese fl ying squid, the mantle observed subsequently up to the encloses the visceral mass of the squid, mammalian class. However, the word and has two enlarged lateral fi ns. The ‘fl ying’ brings to mind pictures of birds squid has eight arms and two tentacles only. with suction cups along the backs. But there are many other fl yers other In between the arms sits the mouth, than birds in the animal kingdom who inside the mouth a rasping organ called have mastered the art of being airborne. radula is present. Squids have ink sacs, Japanese fl ying squid Different body structures and peculiar which they use as a defence mechanism organs contribute to the aerodynamic against predators. Membranes are stability of these organisms. Let’s take present between the tentacles. They 40 cm in length respectively. When a look at some of them. can fl y more than 30 m in 3 seconds they leave water for the air, sea birds uniquely utilising their jet-propelled such as frigates, albatrosses, and gulls aerial locomotion. 1. Gliding ant: Gliding ants are liable to attack. Its body lifts above (Cephalotes atrautus) are arboreal ants the surface, it spread its fi ns and taxis 3. -

A Rapid Survey of Online Trade in Live Birds and Reptiles in The
S H O R T R E P O R T 0ൾඍඁඈൽඌ A rapid online survey was undertaken EHWZHHQDQG)HEUXDU\ GD\V DSSUR[LPDWHO\KRXUVVXUYH\GD\ RQ pre-selected Facebook groups specializing in the trade of live pets. Ten groups each for reptiles and birds were selected based on trading activities in the previous six months. The survey was carried out during ZHHN GD\V 0RQGD\ WR )ULGD\ E\ JRLQJ through each advertisement posted in A rapid survey of online trade in the groups. Information, including that live birds and reptiles in the Philippines relating to species, quantity, and asking HYDROSAURUS PUSTULATUS WWF / URS WOY WOY WWF / URS PUSTULATUS HYDROSAURUS SULFH ZDV QRWHG 6SHFLHV ZHUH LGHQWL¿HG Report by Cristine P. Canlas, Emerson Y. Sy, to the lowest taxonomic level whenever and Serene Chng possible. Taxonomy follows Gill and 'RQVNHU IRU ELUGV DQG 8HW] et al. IRUUHSWLOHV7KHDXWKRUVFDOFXODWHG ,ඇඍඋඈൽඎർඍංඈඇ WKH WRWDO SRWHQWLDO YDOXH R൵HUHG IRU ELUGV and reptiles based on prices indicated he Philippines is the second largest archipelago in the world by traders. Advertisements that did not comprising 7641 islands and is both a mega-biodiverse specify prices were assigned the lowest country for harbouring wildlife species found nowhere known price for each taxon. Valuations in else in the world, and one of eight biodiversity hotspots this report were based on a conversion rate having a disproportionate number of species threatened with RI86' 3+3 $QRQ ,WLV ,//8675$7,213+,/,33,1(6$,/),1/,=$5' TH[WLQFWLRQIXUWKHULWKDVVRPHRIWKHKLJKHVWUDWHVRIHQGHPLFLW\LQWKH not always possible during online surveys world (Myers et al 7KHLOOHJDOZLOGOLIHWUDGHLVRQHRIWKHPDLQ WRYHULI\WKDWDOOR൵HUVDUHJHQXLQH UHDVRQVEHKLQGVLJQL¿FDQWGHFOLQHVRIVRPHZLOGOLIHSRSXODWLRQVLQ$VLD LQFOXGLQJWKH3KLOLSSLQHV $QRQ6RGKLet al1LMPDQDQG 5ൾඌඎඅඍඌ 6KHSKHUG'LHVPRVet al5DRet al 7KHWildlife Act of 2001 (Republic Act No. -

Research Journal of Pharmaceutical, Biological and Chemical
ISSN: 0975-8585 Research Journal of Pharmaceutical, Biological and Chemical Sciences Diversity of Squamates (Scaled Reptiles) in Selected Urban Areas of Cagayan de Oro City, Misamis Oriental. John C Naelga*, Daniel Robert P Tayag, Hazel L Yañez, and Astrid L Sinco. Xavier University – Ateneo De Cagayan, Kinaadman Resource Center. ABSTRACT This study was conducted to provide baseline information on the local urban diversity of squamates in the selected areas of Barangay Kauswagan, Barangay Balulang, and Barangay FS Catanico in Cagayan de Oro City. These urban sites are close to the river and are likely to be inhabited by reptiles. Each site had at least ten (10) points and was sampled no less than five (5) times in the months of September to November 2016 using homemade traps and the Cruising-Transect walk method. One representative per species was preserved. A total of two hundred sixty-seven (267) individuals, grouped into four (4) families and ten (10) species were found in the sampling areas. Six (6) snake species were identified, namely: Boiga cynodon, Naja samarensis, Chrysopelea paradisi, Gonyosoma oxycephalum, Coelegnathus erythrurus eryhtrurus, and Dendrelaphis pictus; while four (4) species were lizards namely: Gekko gecko, Hemidactylus platyurus, Lamprolepis smaragdina philippinica, and Eutropis multifasciata.In Barangay Kauswagan, Hemidactylus platyurus was the most abundant (RA= 52.94%). In Barangay Balulang, the most abundant species was Hemidactylus platyurus (RA= 43.82%). In Barangay FS Catanico, the most abundant was Hemidactylus platyurus (RA= 40.16%). The area with the highest species diversity was Barangay FS Catanico (H= 1.36), followed by Barangay Balulang (H= 1.28), and Barangay Kauswagan (H= 1.08). -
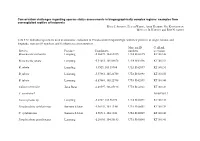
Conservation Challenges Regarding Species Status Assessments in Biogeographically Complex Regions: Examples from Overexploited Reptiles of Indonesia KYLE J
Conservation challenges regarding species status assessments in biogeographically complex regions: examples from overexploited reptiles of Indonesia KYLE J. SHANEY, ELIJAH WOSTL, AMIR HAMIDY, NIA KURNIAWAN MICHAEL B. HARVEY and ERIC N. SMITH TABLE S1 Individual specimens used in taxonomic evaluation of Pseudocalotes tympanistriga, with their province of origin, latitude and longitude, museum ID numbers, and GenBank accession numbers. Museum ID GenBank Species Province Coordinates numbers accession Bronchocela cristatella Lampung -5.36079, 104.63215 UTA R 62895 KT180148 Bronchocela jubata Lampung -5.54653, 105.04678 UTA R 62896 KT180152 B. jubata Lampung -5.5525, 105.18384 UTA R 62897 KT180151 B. jubata Lampung -5.57861, 105.22708 UTA R 62898 KT180150 B. jubata Lampung -5.57861, 105.22708 UTA R 62899 KT180146 Calotes versicolor Jawa Barat -6.49597, 106.85198 UTA R 62861 KT180149 C. versicolor* NC009683.1 Gonocephalus sp. Lampung -5.2787, 104.56198 UTA R 60571 KT180144 Pseudocalotes cybelidermus Sumatra Selatan -4.90149, 104.13401 UTA R 60551 KT180139 P. cybelidermus Sumatra Selatan -4.90711, 104.1348 UTA R 60549 KT180140 Pseudocalotes guttalineatus Lampung -5.28105, 104.56183 UTA R 60540 KT180141 P. guttalineatus Sumatra Selatan -4.90681, 104.13457 UTA R 60501 KT180142 Pseudocalotes rhammanotus Lampung -4.9394, 103.85292 MZB 10804 KT180147 Pseudocalotes species 4 Sumatra Barat -2.04294, 101.31129 MZB 13295 KT211019 Pseudocalotes tympanistriga Jawa Barat -6.74181, 107.0061 UTA R 60544 KT180143 P. tympanistriga Jawa Barat -6.74181, 107.0061 UTA R 60547 KT180145 Pogona vitticeps* AB166795.1 *Entry to GenBank by previous authors TABLE S2 Reptile species currently believed to occur Java and Sumatra, Indonesia, with IUCN Red List status, and certainty of occurrence. -

P. 1 AC27 Inf. 7 (English Only / Únicamente En Inglés / Seulement
AC27 Inf. 7 (English only / únicamente en inglés / seulement en anglais) CONVENTION ON INTERNATIONAL TRADE IN ENDANGERED SPECIES OF WILD FAUNA AND FLORA ____________ Twenty-seventh meeting of the Animals Committee Veracruz (Mexico), 28 April – 3 May 2014 Species trade and conservation IUCN RED LIST ASSESSMENTS OF ASIAN SNAKE SPECIES [DECISION 16.104] 1. The attached information document has been submitted by IUCN (International Union for Conservation of * Nature) . It related to agenda item 19. * The geographical designations employed in this document do not imply the expression of any opinion whatsoever on the part of the CITES Secretariat or the United Nations Environment Programme concerning the legal status of any country, territory, or area, or concerning the delimitation of its frontiers or boundaries. The responsibility for the contents of the document rests exclusively with its author. AC27 Inf. 7 – p. 1 Global Species Programme Tel. +44 (0) 1223 277 966 219c Huntingdon Road Fax +44 (0) 1223 277 845 Cambridge CB3 ODL www.iucn.org United Kingdom IUCN Red List assessments of Asian snake species [Decision 16.104] 1. Introduction 2 2. Summary of published IUCN Red List assessments 3 a. Threats 3 b. Use and Trade 5 c. Overlap between international trade and intentional use being a threat 7 3. Further details on species for which international trade is a potential concern 8 a. Species accounts of threatened and Near Threatened species 8 i. Euprepiophis perlacea – Sichuan Rat Snake 9 ii. Orthriophis moellendorfi – Moellendorff's Trinket Snake 9 iii. Bungarus slowinskii – Red River Krait 10 iv. Laticauda semifasciata – Chinese Sea Snake 10 v. -

Chrysopelea Ornata)
Material properties of skin in a flying snake (Chrysopelea ornata) Sarah Bonham Dellinger Thesis submitted to the faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Master of Science In Engineering Mechanics John J. Socha, Chair Raffaella De Vita Pavlos P. Vlachos April 27, 2011 Blacksburg, VA Keywords: flying snakes, skin, material properties, digital image correlation © Sarah Bonham Dellinger 2011 Material properties of skin in a flying snake (Chrysopelea ornata) Sarah Bonham Dellinger ABSTRACT The genus Chrysopelea encompasses the “flying” snakes. This taxon has the ability to glide via lateral aerial undulation and dorsoventral body flattening, a skill unique to this group, but in addition to other functions common to all colubrids. The skin must be extensible enough to allow this body shape alteration and undulation, and strong enough to withstand the forces seen during landing. For this reason, characterizing the mechanical properties of the skin may give insight to the functional capabilities of the skin during these gliding and landing behaviors. Dynamic and viscoelastic uniaxial tensile tests were combined with a modified particle image velocimetry technique to provide strength, extensibility, strain energy, and stiffness information about the skin with respect to orientation, region, and species, along with viscoelastic parameters. Results compared with two other species in this study and a broader range of species in prior studies indicate that while the skin of these unique snakes may not be specifically specialized to deal with larger forces, extensibility, or energy storage and release, the skin does have increased strength and energy storage associated with higher strain rates. -

Reptiles of Phetchaburi Province, Western Thailand: a List of Species, with Natural History Notes, and a Discussion on the Biogeography at the Isthmus of Kra
The Natural History Journal of Chulalongkorn University 3(1): 23-53, April 2003 ©2003 by Chulalongkorn University Reptiles of Phetchaburi Province, Western Thailand: a list of species, with natural history notes, and a discussion on the biogeography at the Isthmus of Kra OLIVIER S.G. PAUWELS 1*, PATRICK DAVID 2, CHUCHEEP CHIMSUNCHART 3 AND KUMTHORN THIRAKHUPT 4 1 Department of Recent Vertebrates, Institut Royal des Sciences naturelles de Belgique, 29 rue Vautier, 1000 Brussels, BELGIUM 2 UMS 602 Taxinomie-collection – Reptiles & Amphibiens, Muséum National d’Histoire Naturelle, 25 rue Cuvier, 75005 Paris, FRANCE 3 65 Moo 1, Tumbon Tumlu, Amphoe Ban Lat, Phetchaburi 76150, THAILAND 4 Department of Biology, Faculty of Science, Chulalongkorn University, Bangkok 10330, THAILAND ABSTRACT.–A study of herpetological biodiversity was conducted in Phetcha- buri Province, in the upper part of peninsular Thailand. On the basis of a review of available literature, original field observations and examination of museum collections, a preliminary list of 81 species (12 chelonians, 2 crocodiles, 23 lizards, and 44 snakes) is established, of which 52 (64 %) are reported from the province for the first time. The possible presence of additional species is discussed. Some biological data on the new specimens are provided including some range extensions and new size records. The herpetofauna of Phetchaburi shows strong Sundaic affinities, with about 88 % of the recorded species being also found south of the Isthmus of Kra. A biogeographic affinity analysis suggests that the Isthmus of Kra plays the role of a biogeographic filter, due both to the repeated changes in climate during the Quaternary and to the current increase of the dry season duration along the peninsula from south to north. -

Tangled Skeins: a First Report of Non-Captive Mating Behavior in the Southeast Asian Paradise Flying Snake (Reptilia: Squamata: Colubridae: Chrysopelea Paradisi)
OPEN ACCESS All articles published in the Journal of Threatened Taxa are registered under Creative Commons Attribution 4.0 Interna- tional License unless otherwise mentioned. JoTT allows unrestricted use of articles in any medium, reproduction and distribution by providing adequate credit to the authors and the source of publication. Journal of Threatened Taxa The international journal of conservation and taxonomy www.threatenedtaxa.org ISSN 0974-7907 (Online) | ISSN 0974-7893 (Print) Short Communication Tangled skeins: a first report of non-captive mating behavior in the Southeast Asian Paradise Flying Snake (Reptilia: Squamata: Colubridae: Chrysopelea paradisi) Hinrich Kaiser, Johnny Lim, Heike Worth & Mark O’Shea 26 February 2016 | Vol. 8 | No. 2 | Pp. 8488–8494 10.11609/jott.2440.8.2.8488-8494 For Focus, Scope, Aims, Policies and Guidelines visit http://threatenedtaxa.org/About_JoTT.asp For Article Submission Guidelines visit http://threatenedtaxa.org/Submission_Guidelines.asp For Policies against Scientific Misconduct visit http://threatenedtaxa.org/JoTT_Policy_against_Scientific_Misconduct.asp For reprints contact <[email protected]> Publisher/Host Partner Threatened Taxa Journal of Threatened Taxa | www.threatenedtaxa.org | 26 February 2016 | 8(2): 8488–8494 Tangled skeins: a first report of non-captive mating behavior in the Southeast Asian Paradise Flying Snake ISSN 0974-7907 (Online) (Reptilia: Squamata: Colubridae: Chrysopelea paradisi) Short Communication Short ISSN 0974-7893 (Print) Hinrich Kaiser 1, Johnny Lim 2, Heike