Primer on Flat Rolling Primer on Flat Rolling Second Edition
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Influence of Tool Shape and Process Parameters on The
materials Article The Influence of Tool Shape and Process Parameters on the Mechanical Properties of AW-3004 Aluminium Alloy Friction Stir Welded Joints Anna Janeczek , Jacek Tomków * and Dariusz Fydrych Institute of Machines and Materials Technology, Faculty of Mechanical Engineering and Ship Technology, Gda´nskUniversity of Technology, Gabriela Narutowicza Street 11/12, 80-233 Gda´nsk,Poland; [email protected] (A.J.); [email protected] (D.F.) * Correspondence: [email protected]; Tel.: +48-58-347-10-32 Abstract: The purpose of the following study was to compare the effect of the shape of a tool on the joint and to obtain the values of Friction Stir Welding (FSW) parameters that provide the best possible joint quality. The material used was an aluminium alloy, EN AW-3004 (AlMn1Mg1). To the authors’ best knowledge, no investigations of this alloy during FSW have been presented earlier. Five butt joints were made with a self-developed, cylindrical, and tapered threaded tool with a rotational speed of 475 rpm. In order to compare the welding parameters, two more joints with a rotational speed of 475 rpm and seven joints with a welding speed of 300 mm/min with the use of a cylindrical threaded pin were performed. This involved a visual inspection as well as a tensile strength test of the welded joints. It was observed that the value of the material outflow for the joints made with the cylindrical threaded pin was higher than it was for the joints made with the tapered threaded pin. However, welding defects in the form of voids appeared in the joints made with the tapered threaded tool. -

(12) United States Patent (10) Patent No.: US 7,507,480 B2 Sugama (45) Date of Patent: Mar
USOO7507480B2 (12) United States Patent (10) Patent No.: US 7,507,480 B2 Sugama (45) Date of Patent: Mar. 24, 2009 (54) CORROSION-RESISTANT METAL SURFACES 6,239,205 B1 5/2001 Hasegawa et al. 6,254,980 B1 7/2001 Tadokoro et al. (75) Inventor: Toshifumi Sugama, Wading River, NY 6,297.302 B1 10/2001 Heeks et al. (US) 6,312,812 B1 1 1/2001 Hauser et al. 6,469,119 B2 10/2002 Basil et al. (73) Assignee: Brookhaven Science Associates, LLC, 6,551482 B2 4/2003 Yamamoto et al. Upton, NY (US) 6,554,989 B2 4/2003 Muramoto et al. 6,608, 129 B1 8, 2003 Koloski et al. (*) Notice: Subject to any disclaimer, the term of this 6,686,406 B2 2/2004 Tomomatsu et al. patent is extended or adjusted under 35 6,716,895 B1 4/2004 Terry U.S.C. 154(b) by 597 days. 6,749,945 B2 6/2004 Knobbe et al. 6,770,690 B2 8/2004 Fujiki et al. (21) Appl. No.: 11/141,674 2001/0006731 A1 7/2001 Basil et al. 2002/O121442 A1 9, 2002 Muramoto et al. (22) Filed: May 31, 2005 2002/0136911 A1 9/2002 Yamamoto et al. 2003/00928.12 A1 5/2003 Nakada et al. (65) Prior Publication Data 2004/0022950 A1 2/2004 Jung et al. 2004/0116551 A1 6/2004 Terry US 2006/026976O A1 Nov.30, 2006 (51) Int. Cl. FOREIGN PATENT DOCUMENTS CSK 3/22 (2006.01) AU 3.2947/84 3, 1985 (52) U.S. -

COST 507 Thermophysical Properties of Light Metal Alloys
COST 507 Thermophysical Properties of Light Metal Alloys Gra zy na J a ro ma-We i Ia nd Rud iger Bra ndt Gunther Neuer DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available original document. COST 507 Thermophysical Properties of Light Metal Alloys Final Report Grazyna Jaroma-Wei la nd Rudiger Brandt Gunther Neuer Under Contract of BMFT 03K075 ISSN 01 73-6698 ASTE February 1994 IKE 5 - 238 Un iversita t Stu ttgart ABSTRACT The thermophysical properties of AI-,Mg- and Ti-based light m studied by reviewing the literature published so far, evaluatin and by empirical investigations. The properties to be covered in are: thermal conductivity, thermal diffusivity, specific heat capacity, thermal expansion and electrical resistivity. The data have been stored in the factual data base THERSYST together with the results of experimental measurements supplied from participants of the COST 507 - action (Group D). Altogether 1325 data-sets referring to 146 alloys have been stored. They have been uniformly represented and critically analyzed by means of the THERSYST program moduli. These numerical data cover a number of systems with variing and thermal treatment. Partly large discrepancies especi conductivity have been found for similar alloyflry often the in corresponding publications are not complete enough to identify whether such discrepancies can be explained by other material related characteristics, such as thermal pretreatment etc. or whether experimental reasons are responsible. Therefore additional measurements are necessary in order to enable reliable statements upon variation of thermophysical properties (especially thermal conductivity) with chemical composition and microstructure. -

CUMULATIVE INDEX September 1952 Through December 2017
Materials Park, Ohio 44073-0002 :: 440.338.5151 :: Fax 440.338.8542 :: www.asminternational.org :: [email protected] Published by ASM International® :: Data shown are typical, not to be used for specification or final design. CUMULATIVE INDEX September 1952 through December 2017 Alphabetical listing by tradename or other designation and code number Alloy Steel Aluminum Beryllium Bismuth Carbon Steel Cast Iron Ceramic Chromium Cobalt Copper Gold Iron Lead Magnesium Molybdenum Nickel Neodymium Plastic Silver Stainless Steel Tin Titanium Tool Steel Tungsten Zinc Contents Alphabetical Index by Material Name Pages 3 through 35 Alphabetical Index within Material Group Pages 39 through 70 Copyright © 2017, ASM International®. All rights reserved. Published by ASM International® Materials Park, Ohio 44073-0002 [email protected] 440-338-5151, Fax 440-338-8542 www.asminternational.org Copyright © 2018 ASM International® All rights reserved No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the written permission of the copyright owner. Great care is taken in the compilation and production of this publication, but it should be made clear that NO WARRANTIES, EXPRESS OR IMPLIED, INCLUDING, WITHOUT LIMITATION, WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE, ARE GIVEN IN CONNECTION WITH THIS PUBLICATION. Although this information is believed to be accurate by ASM, ASM cannot guarantee that favorable results will be obtained from the use of this publication alone. This publication is intended for use by persons having technical skill, at their sole discretion and risk. Since the conditions of product or material use are outside of ASM’s control, ASM assumes no liability or obligation in connection with any use of this information. -

CORROSION-OF-ALUMINIUM.Pdf
CORROSION OF ALUMINIUM Elsevier Internet Homepage- http://www.elsevier.com Consult the Elsevier homepage for full catalogue information on all books, journals and electronic products and services including further information about the publications listed below. Elsevier titles of related interest Books KASSNER Fundamentals of Creep in Metals and Alloys 2004. ISBN: 0080436374 HUMPHREYS AND HATHERLEY Recrystallization and Related Annealing Phenomena, 2nd Edition 2004. ISBN: 008-044164-5 GALE Smithells Metals Reference Book, 8th Edition 2003. ISBN 0-7506-7509-8 Elsevier author discount Elsevier authors (of books and journal papers) are entitled to a 30% discount off the above books and most others. See ordering instructions below. Journals Sample copies of all Elsevier journals can be viewed online for FREE at www.sciencedirect.com, by visiting the journal homepage. Journals of Alloys & Compounds Corrosion Science International Journal of Fatigue Electrochimica Acta To contact the Publisher: Elsevier welcomes enquiries concerning publishing proposals: books, journal special issues, conference proceedings, etc. All formats and media can be considered. Should you have a publishing proposal you wish to discuss, please contact, without obligation, the publisher responsible for Elsevier’s material science programme: David Sleeman Publishing Editor Elsevier Ltd The Boulevard, Langford Lane Phone: +44 1865 843265 Kidlington, Oxford Fax: +44 1865 843920 OX5 1GB, UK E.mail: [email protected] General enquiries, including placing orders, should be directed to Elsevier’s Regional Sales Offices-please access the Elsevier homepage for full contact details www.elsevier.com CORROSION OF ALUMINIUM Christian Vargel Consulting Engineer, Member of the Commission of Experts within the International Chamber of Commerce, Paris, France http://www.corrosion-aluminium.com Foreword by Michel Jacques President, Alcan Engineered Products Translated by Dr. -
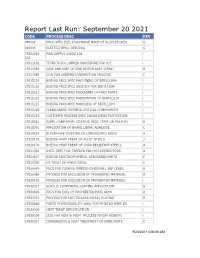
Process Specifications
Report Last Run: September 20 2021 CODE PROCESS DESC REV 940004 PROC SPEC-ELEC DISCHARGE MACH OF ALUM,ST,CRES G 940005 ELECTRCHEMCL DEBURRG G CPS04082- PWR SUPPLY 24VDC 10A - 10A CPS11192 TITAN IV LCU JUMPER PROCEDURE INV U13 - CPS11983 ASSY AND INSP OF GMD ROTOR ASSY 17E647 B CPS11989 COIL FAB ASSEMBLY/INSPECTION PROCESS C CPS15219 BOEING PRCS SPEC MACHINING OF BERYLLIUM - CPS15220 BOEING PRCS SPEC ANODIZE FOR BERYLLIUM - CPS15221 BOEING PRCS SPEC PACKAGING OF PREC PARTS - CPS15222 BOEING PRCS SPEC PASSIVATION OF BERYLLIUM - CPS15225 BOEING PRCS SPEC HANDLING OF BERYLLIUM - CPS15249 CLEANLINESS CRITERIA CRITICAL COMPONENTS - CPS15253 CUSTOMER PROCESS SPEC CLEANLINESS PROTECTION - CPS18682 SUPPL CONFORMAL COATING PROC (TYPE UR POLYUR) B CPS18701 APPLICATION OF BRAKE LINING ADHESIVE C CPS19824 BLACKHAWK RIVETING OF LINKAGE/BRG ASSYS A CPS20175 BOEING HEAT TREAT OF ALLOY STEELS J CPS20176 BOEING HEAT TREAT OF CORR RESISTANT STEELS A CPS22356 INSTL SPEC FOR TAPERED PIN HYD RESTRICTORS A CPS24677 BOEING ELECTROCHEMICAL DEBURRING PARTS C CPS25390 HT TREAT OF 4340M STEEL C CPS26474 PRCS FOR CLEAN & IMPREGN PHEN BALL SEP CERES A CPS26480 PROCESS FOR EXCLUSION OF PROHIBITED MATERIAL A CPS30150 PROCESS FOR EXCLUSION OF PROHIBITED MATERIAL - CPS30313 ACRYLIC CONFORMAL COATING APPLICATION B CPS30606 PRCS FOR EXCL OF PROHIBITED MATL AEHV A CPS37037 PROCESS FOR ELECTROLESS NICKEL PLATING B CPS38888 PARTS PRODUCEABILITY ANAL FOR PRINTED WIRE BD - CPS39204 HEAT TREAT SPECIFICATION - CPS39209 COIL FAB ASSY & INSPT PROCESS (ENCAP BOBBIN) - CPS40357 CARBURIZING