Some Constraints Assuring Serializability in Multidatabases
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Concurrency Control Basics
Outline l Introduction/problems, l definitions Introduction/ (transaction, history, conflict, equivalence, Problems serializability, ...), Definitions l locking. Chapter 2: Locking Concurrency Control Basics Klemens Böhm Distributed Data Management: Concurrency Control Basics – 1 Klemens Böhm Distributed Data Management: Concurrency Control Basics – 2 Atomicity, Isolation Synchronisation, Distributed (1) l Transactional guarantees – l Essential feature of databases: in particular, atomicity and isolation. Many users can access the same data concurrently – be it read, be it write. Introduction/ l Atomicity Introduction/ Problems Problems u Example, „bank scenario“: l Consistency must be guaranteed – Definitions Definitions task of synchronization component. Locking Number Person Balance Locking Klemens 5000 l Multi-user mode shall be hidden from users as far as possible: concurrent processing Gunter 200 of requests shall be transparent, u Money transfer – two elementary operations. ‚illusion‘ of being the only user. – debit(Klemens, 500), – credit(Gunter, 500). l Isolation – can be explained with this example, too. l Transactions. Klemens Böhm Distributed Data Management: Concurrency Control Basics – 3 Klemens Böhm Distributed Data Management: Concurrency Control Basics – 4 Synchronisation, Distributed (2) Synchronization in General l Serial execution of application programs Uncontrolled non-serial execution u achieves that illusion leads to other problems, notably inconsistency: l Introduction/ without any synchronization effort, Introduction/ -

Cache Serializability: Reducing Inconsistency in Edge Transactions
Cache Serializability: Reducing Inconsistency in Edge Transactions Ittay Eyal Ken Birman Robbert van Renesse Cornell University tributed databases. Until recently, technical chal- Abstract—Read-only caches are widely used in cloud lenges have forced such large-system operators infrastructures to reduce access latency and load on to forgo transactional consistency, providing per- backend databases. Operators view coherent caches as object consistency instead, often with some form of impractical at genuinely large scale and many client- facing caches are updated in an asynchronous manner eventual consistency. In contrast, backend systems with best-effort pipelines. Existing solutions that support often support transactions with guarantees such as cache consistency are inapplicable to this scenario since snapshot isolation and even full transactional atom- they require a round trip to the database on every cache icity [9], [4], [11], [10]. transaction. Our work begins with the observation that it can Existing incoherent cache technologies are oblivious to be difficult for client-tier applications to leverage transactional data access, even if the backend database supports transactions. We propose T-Cache, a novel the transactions that the databases provide: trans- caching policy for read-only transactions in which incon- actional reads satisfied primarily from edge caches sistency is tolerable (won’t cause safety violations) but cannot guarantee coherency. Yet, by running from undesirable (has a cost). T-Cache improves cache consis- cache, client-tier transactions shield the backend tency despite asynchronous and unreliable communication database from excessive load, and because caches between the cache and the database. We define cache- are typically placed close to the clients, response serializability, a variant of serializability that is suitable latency can be improved. -

A Theory of Global Concurrency Control in Multidatabase Systems
VLDB Journal,2, 331-360 (1993), Michael Carey and Patrick Valduriez, Editors 331 t~)VLDB A Theory of Global Concurrency Control in Multidatabase Systems Aidong Zhang and Ahmed K. Elmagarmid Received December 1, 1992; revised version received February 1, 1992; accepted March 15, 1993. Abstract. This article presents a theoretical basis for global concurrency control to maintain global serializability in multidatabase systems. Three correctness criteria are formulated that utilize the intrinsic characteristics of global transactions to de- termine the serialization order of global subtransactions at each local site. In par- ticular, two new types of serializability, chain-conflicting serializability and shar- ing serializability, are proposed and hybrid serializability, which combines these two basic criteria, is discussed. These criteria offer the advantage of imposing no restrictions on local sites other than local serializability while retaining global se- rializability. The graph testing techniques of the three criteria are provided as guidance for global transaction scheduling. In addition, an optimal property of global transactions for determinating the serialization order of global subtransac- tions at local sites is formulated. This property defines the upper limit on global serializability in multidatabase systems. Key Words. Chain-conflicting serializability, sharing serializability, hybrid serial- izability, optimality. 1. Introduction Centralized databases were predominant during the 1970s, a period which saw the development of diverse database systems based on relational, hierarchical, and network models. The advent of applications involving increased cooperation between systems necessitated the development of methods for integrating these pre-existing database systems. The design of such global database systems must allow unified access to these diverse database systems without subjecting them to conversion or major modifications. -

Chapter 14: Concurrency Control
ChapterChapter 1515 :: ConcurrencyConcurrency ControlControl What is concurrency? • Multiple 'pieces of code' accessing the same data at the same time • Key issue in multi-processor systems (i.e. most computers today) • Key issue for parallel databases • Main question: how do we ensure data stay consistent without sacrificing (too much) performance? Lock-BasedLock-Based ProtocolsProtocols • A lock is a mechanism to control concurrent access to a data item • Data items can be locked in two modes: 1. exclusive (X) mode. Data item can be both read as well as written. X-lock is requested using lock-X instruction. 2. shared (S) mode. Data item can only be read. S-lock is requested using lock-S instruction. • Lock requests are made to concurrency-control manager. Transaction can proceed only after request is granted. Lock-BasedLock-Based ProtocolsProtocols (Cont.)(Cont.) • Lock-compatibility matrix • A transaction may be granted a lock on an item if the requested lock is compatible with locks already held on the item by other transactions. • Any number of transactions can hold shared locks on an item, – but if any transaction holds an exclusive on the item no other transaction may hold any lock on the item. • If a lock cannot be granted, the requesting transaction is made to wait till all incompatible locks held by other transactions have been released. The lock is then granted. Lock-BasedLock-Based ProtocolsProtocols (Cont.)(Cont.) • Example of a transaction performing locking: T2: lock-S(A); read (A); unlock(A); lock-S(B); read (B); unlock(B); display(A+B) • Locking as above is not sufficient to guarantee serializability — if A and B get updated in-between the read of A and B, the displayed sum would be wrong. -

Analysis and Comparison of Concurrency Control Techniques
ISSN (Online) 2278-1021 ISSN (Print) 2319-5940 International Journal of Advanced Research in Computer and Communication Engineering Vol. 4, Issue 3, March 2015 Analysis and Comparison of Concurrency Control Techniques Sonal Kanungo1, Morena Rustom. D2 Smt.Z.S.Patel College Of Computer, Application,Jakat Naka, Surat1 2 Department Of Computer Science, Veer Narmad South Gujarat University, Surat. Abstract: In a shared database system when several transactions are executed simultaneously, the consistency of database should be maintained. The techniques to ensure this consistency are concurrency control techniques. All concurrency-control schemes are based on the serializability property. The serializability properties requires that the data is accessed in a mutually exclusive manner; that means, while one transaction is accessing a data item no other transaction can modify that data item. In this paper we had discussed various concurrency techniques, their advantages and disadvantages and making comparison of optimistic, pessimistic and multiversion techniques. We have simulated the current environment and have analysis the performance of each of these methods. Keywords: Concurrency, Locking, Serializability 1. INTRODUCTION When a transaction takes place the database state is transaction has to wait until all incompatible locks held by changed. In any individual transaction, which is running other transactions are released. The lock is then granted. in isolation, is assumed to be correct. While in shared [1] database several transactions are executes concurrently in 1.1.2 The Two-Phase Locking Protocol the database, the isolation property may no longer be Transaction can always commit by not violating the preserved. To ensure that the system must control the serializability property. -

Where We Are Snapshot Isolation Snapshot Isolation
Where We Are • ACID properties of transactions CSE 444: Database Internals • Concept of serializability • How to provide serializability with locking • Lowers level of isolation with locking • How to provide serializability with optimistic cc Lectures 16 – Timestamps/Multiversion or Validation Transactions: Snapshot Isolation • Today: lower level of isolation with multiversion cc – Snapshot isolation Magda Balazinska - CSE 444, Spring 2012 1 Magda Balazinska - CSE 444, Spring 2012 2 Snapshot Isolation Snapshot Isolation • Not described in the book, but good overview in Wikipedia • A type of multiversion concurrency control algorithm • Provides yet another level of isolation • Very efficient, and very popular – Oracle, PostgreSQL, SQL Server 2005 • Prevents many classical anomalies BUT… • Not serializable (!), yet ORACLE and PostgreSQL use it even for SERIALIZABLE transactions! – But “serializable snapshot isolation” now in PostgreSQL Magda Balazinska - CSE 444, Fall 2010 3 Magda Balazinska - CSE 444, Fall 2010 4 Snapshot Isolation Rules Snapshot Isolation (Details) • Multiversion concurrency control: • Each transactions receives a timestamp TS(T) – Versions of X: Xt1, Xt2, Xt3, . • Transaction T sees snapshot at time TS(T) of the database • When T reads X, return XTS(T). • When T commits, updated pages are written to disk • When T writes X: if other transaction updated X, abort – Not faithful to “first committer” rule, because the other transaction U might have committed after T. But once we abort • Write/write conflicts resolved by “first -

An Evaluation of Distributed Concurrency Control
An Evaluation of Distributed Concurrency Control Rachael Harding Dana Van Aken MIT CSAIL Carnegie Mellon University [email protected] [email protected] Andrew Pavlo Michael Stonebraker Carnegie Mellon University MIT CSAIL [email protected] [email protected] ABSTRACT there is little understanding of the trade-offs in a modern cloud Increasing transaction volumes have led to a resurgence of interest computing environment offering high scalability and elasticity. Few in distributed transaction processing. In particular, partitioning data of the recent publications that propose new distributed protocols across several servers can improve throughput by allowing servers compare more than one other approach. For example, none of the to process transactions in parallel. But executing transactions across papers published since 2012 in Table 1 compare against timestamp- servers limits the scalability and performance of these systems. based or multi-version protocols, and seven of them do not compare In this paper, we quantify the effects of distribution on concur- to any other serializable protocol. As a result, it is difficult to rency control protocols in a distributed environment. We evaluate six compare proposed protocols, especially as hardware and workload classic and modern protocols in an in-memory distributed database configurations vary across publications. evaluation framework called Deneva, providing an apples-to-apples Our aim is to quantify and compare existing distributed concur- comparison between each. Our results expose severe limitations of rency control protocols for in-memory DBMSs. We develop an distributed transaction processing engines. Moreover, in our anal- empirical understanding of the behavior of distributed transactions ysis, we identify several protocol-specific scalability bottlenecks. -

A Drop-In Middleware for Serializable DB Clustering Across Geo-Distributed Sites
A Drop-in Middleware for Serializable DB Clustering across Geo-distributed Sites Enrique Saurez1, Bharath Balasubramanian2, Richard Schlichting3 Brendan Tschaen2 Shankaranarayanan Puzhavakath Narayanan,2 Zhe Huang2, Umakishore Ramachandran1 Georgia Institute of Technology1 AT&T Labs - Research2 United States Naval Academy3 [email protected], [email protected], [email protected], [email protected], fsnarayanan, [email protected], [email protected] ABSTRACT formance needs of clients.1 However, many of these services Many geo-distributed services at web-scale companies still use databases (DBs) like MariaDB [54] and PostgreSQL [50] rely on databases (DBs) primarily optimized for single-site that are primarily optimized for single site deployments even performance. At AT&T this is exemplified by services in the when they have clustering solutions. For eample, in Mari- network control plane that rely on third-party software that aDB Galera [28] synchronous clustering [29] all replicas are uses DBs like MariaDB and PostgreSQL, which do not pro- updated on each commit, which is prohibitively expensive vide strict serializability across sites without a significant across sites with WAN latencies on the order of hundreds performance impact. Moreover, it is often impractical for of milliseconds. Similarly, in PostgreSQL master-slave [49] these services to re-purpose their code to use newer DBs op- clustering, requests from all sites are sent to a single master timized for geo-distribution. In this paper, a novel drop-in replica, compromising on performance and availability. solution for DB clustering across sites called Metric is pre- Although new geo-distributed DBs have been developed sented that can be used by services without changing a single that improve the performance of cross-site transactionality line of code. -

Relative Serializability: an Approach for Relaxing the Atomicityoftransactions
Relative Serializability: An Approach for Relaxing the AtomicityofTransactions D. Agrawal J. L. Bruno A. El Abbadi V. Krishnaswamy Department of Computer Science University of California Santa Barbara, CA 93106 Abstract In the presence of semantic information, serializabil i ty is to o strong a correctness criterion and un- necessarily restricts concurrency.We use the semantic information of a transaction to provide di erent atomicity views of the transaction to other transactions. The prop osed approachimproves concurrency and allows interleaving s among transactions which are non-serializabl e, but which nonetheless preserve the consistency of the database and are acceptable to the users. We develop a graph-based to ol whose acyclicity is b oth a necessary and sucient condition for the correctness of an execution. Our theory encompasses earlier prop osals that incorp orate semantic information of transactions. Furthermore it is the rst approach that provides an ecient graph based to ol for recognizing correct schedules without im- p osing any restrictions on the application domain. Our approach is widely applicabl e to manyadvanced database application s such as systems with long-lived transactions and collab orativeenvironments. 1 Intro duction The traditional approach for transaction managementinmulti-user database systems is to maintain entire transactions as single atomic units with resp ect to each other. Such atomicity of transactions is enforced in most commercial database systems by ensuring that the interleaved execution of concurrent transactions re- mains serializable [EGLT76, RSL78,Pap79, BSW79]. Databases are increasingly used in applications, where transactions may b e long lived, or where transactions corresp ond to executions of various users co op erating with each other, e.g., in design databases, CAD/CAM databases, etc. -

Serializability and Heterogeneous Trust from Two Phase Commit to Blockchains
SERIALIZABILITY AND HETEROGENEOUS TRUST FROM TWO PHASE COMMIT TO BLOCKCHAINS A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy by Isaac Cameron Sheff August 2019 © 2019 Isaac Cameron Sheff ALL RIGHTS RESERVED SERIALIZABILITY AND HETEROGENEOUS TRUST FROM TWO PHASE COMMIT TO BLOCKCHAINS Isaac Cameron Sheff, Ph.D. Cornell University 2019 As distributed systems become more federated and cross-domain, we are forced to rethink some of our core abstractions. We need heterogeneous systems with rig- orous consistency and self-authentication guarantees, despite a complex landscape of security and failure tolerance assumptions. I have designed, built, and evalu- ated heterogeneous distributed algorithms with broad applications from medical privacy to blockchains. This dissertation examines three novel building blocks for this vision. First, I show that serializable transactions cannot always be securely scheduled when data has different levels of confidentiality. I have identified a useful subset of transactions that can always be securely scheduled, and built a system to check and execute them. Second, I present Charlotte, a heterogeneous system that supports compos- able Authenticated Distributed Data Structures (like Git, PKIs, or Bitcoin). I show that Charlotte produces significant performance improvements compared to a single, universally trusted blockchain. Finally, I develop a rigorous generalization of the consensus problem, and present the first distributed consensus which tolerates heterogeneous failures, het- erogeneous participants, and heterogeneous observers. With this consensus, cross- domain systems can maintain ADDSs, or schedule transactions, without the ex- pensive overhead that comes from tolerating the sum of everyone's fears. -
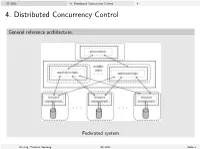
4. Distributed Concurrency Control 4
SS 2013 4. Distributed Concurrency Control 4. 4. Distributed Concurrency Control General reference architecture. Federated system Dr.-Ing. Thomas Hornung SS 2013 Seite 1 SS 2013 4. Distributed Concurrency Control 4.1. Preliminaries 4.1: Preliminaries Sites and subtransactions I Let be given a fixed number of sites across which the data is distributed. The server at site i, 1 ≤ i ≤ n is responsible for a (finite) set Di of data items. The n corresponding global database is given as D = [i=1Di . I Data items are not replicated; thus Di \ Dj = ;, i 6= j. I Let T = fT1;:::; Tmg be a set of transactions, where Ti = (OPi ; <i ), 1 ≤ i ≤ m. I Transaction Ti is called global, if its actions are running at more than one server; otherwise it is called local. I The part of a transaction Ti being executed at a certain site j is called subtransaction and is denoted by Tij . Dr.-Ing. Thomas Hornung SS 2013 Seite 2 SS 2013 4. Distributed Concurrency Control 4.1. Preliminaries Local and global schedules We are interested in deciding whether or not the execution of a set of transactions is serializable, or not. I At the local sites we can observe an evolving sequence of the respective transactions' actions. I We would like to decide whether or not all these locally observable sequences imply a (globally) serializable schedule. I However, on the global level we cannot observe an evolving sequence, as there does not exist a notion of global physical time. Dr.-Ing. Thomas Hornung SS 2013 Seite 3 SS 2013 4. -

Serializable Snapshot Isolation for Replicated Databases in High-Update Scenarios
Serializable Snapshot Isolation for Replicated Databases in High-Update Scenarios Hyungsoo Jungy Hyuck Han∗ Alan Feketey Uwe Rohm¨ y University of Sydney Seoul National University University of Sydney University of Sydney yffi[email protected] ∗[email protected] ABSTRACT pects of this work. Among these is the value of Snapshot Many proposals for managing replicated data use sites run- Isolation (SI) rather than serializability. SI is widely avail- ning the Snapshot Isolation (SI) concurrency control mech- able in DBMS engines like Oracle DB, PostgreSQL, and Mi- anism, and provide 1-copy SI or something similar, as the crosoft SQL Server. By using SI in each replica, and deliver- global isolation level. This allows good scalability, since only ing 1-copy SI as the global behavior, most recent proposals ww-conflicts need to be managed globally. However, 1-copy have obtained improved scalability, since local SI can be SI can lead to data corruption and violation of integrity con- combined into (some variant of) global 1-copy SI by han- straints [5]. 1-copy serializability is the global correctness dling ww-conflicts, but ignoring rw-conflicts. This has been condition that prevents data corruption. We propose a new the dominant replication approach, in the literature [10, 11, algorithm Replicated Serializable Snapshot Isolation (RSSI) 12, 13, 23, 27]. that uses SI at each site, and combines this with a certifi- While there are good reasons for replication to make use cation algorithm to guarantee 1-copy serializable global ex- of SI as a local isolation level (in particular, it is the best ecution.