DOCSLIB.ORG

Notes on the Second Derivative Test

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Notes on the Second Derivative Test Notes on the Second Derivative Test If f(x1; : : : ; xn) is a real-valued function of several real variables, whose second partial derivatives at a point at the point p = (a1; : : : ; an) exist, then the Hessian matrix of f at p is the matrix of second partials 2 3 2 3 @11f(p) @12f(p) ··· @1nf(p) fx1x1 (p) fx1x2 (p) ··· fx1xn (p) 6 @21f(p) @22f(p) @2nf(p) 7 6fx x (p) fx x (p) fx x (p)7 6 7 6 2 1 2 2 2 n 7 H = 6 . .. 7 = 6 . .. 7 : 4 . 5 4 . 5 fxnx1 (p) fxnx2 (p) ··· fxnxn (p) fxnx1 (p) fxnx2 (p) ··· fxnxn (p) If the second partials are continuous in a ball around p, then mixed partials are equal, so H is a symmetric real matrix. 24 2 03 Example 1. If f(x; y; z) = x2y + y2z and p = (1; 2; 3), then H = 42 6 45 : (Check!) 0 4 0 Linear Algebra Terminology/Facts. (1) An n × n real matrix has n special associated values, complex numbers called eigenvalues. (Definition omitted.) An n×n real symmetric matrix has real eigenvalues. The eigenvalues of a diagonal matrix are its diagonal entries. (2) A real symmetric matrix is positive definite if its eigenvalues are positive. It is positive semidefinite if its eigenvalues are positive or zero. It is negative definite if its eigenvalues are negative. It is negative semidefinite if its eigenvalues are negative or zero. It is indefinite if it has at least one positive eigenvalue and at least one negative eigenvalue. Second Derivative Test. Assume p is a critical point of f, and the Hessian matrix of f at p has continuous second partials in a ball around p. • If H is positive definite, then f has a local min at p. • If H is negative definite, then f has a local max at p. • If H is indefinite, then f has a saddle at p. • If H is semidefinite, then the test fails. There are some quick tests for when a matrix H satisfies these conditions. The principal minors 2 3 fx1x1 fx1x2 fx1x3 fx1x1 fx1x2 for the Hessian H are H1 = fx1x1 ;H2 = ;H3 = 4fx2x1 fx2x2 fx2x3 5 ; ETC. fx2x1 fx2x2 fx3x1 fx3x2 fx3x3 • H is positive definite if the determinants of all principal minors, det(H1); det(H2);::: are positive. [This is a theorem, not a definition.] • H is negative definite if the determinants of the principal minors have alternating signs, −; +; −; +; ··· (starting with −). [A theorem.] • IF H = H2 is a 2 × 2 matrix, then H is indefinite if det(H) < 0. [A theorem.] • IF H is a 2 × 2 matrix, and det(H) = 0, then H is semidefinite, and the 2nd Derivative Test fails. 1 2 Exercise. Find and classify the critical points of f(x; y; z) = x2 + 2xy + 2xz + 2y2 + 4yz + 3z2. Solution. rf(x; y; z) = h2x + 2y + 2z; 2x + 4y + 4z; 2x + 4y + 6zi. This exists for every point (x; y; z), so the critical points of f are the points p for which rf(p) = 0. If you set rf = 0, and solve some equations, you find that p = (0; 0; 0) is the only point where rf(p) = 0, so it is the only critical point. 22 2 23 The Hessian matrix at p = 0 is H = 42 4 45 : The principal minors are 2 4 6 22 2 23 2 2 H = 2 ;H = ;H = 2 4 4 : 1 2 2 4 3 4 5 2 4 6 Their determinants are det(H1) = 2; det(H2) = 4; det(H3) = 8. These are all positive, so H is positive definite. This implies that f has a local minimum at (0; 0; 0). Test your understanding. Let f(x; y) = cos(x) + y sin(x) − y2. (1) Show that p = (0; 0) and q = (π; 0) are critical points of f. −1 1 1 −1 (2) Find the Hessians at p and q. You should get H(p) = ;H(q) = : 1 −2 −1 −2 (3) Classify the critical points p and q. (Circle the correct answer or write \Test fails.") (a) p is a local max/local min/saddle point. (b) q is a local max/local min/saddle point..
Load more

Recommended publications
  • The Mean Value Theorem Math 120 Calculus I Fall 2015
    The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0.
    [Show full text]
  • AP Calculus AB Topic List 1. Limits Algebraically 2. Limits Graphically 3
    AP Calculus AB Topic List 1. Limits algebraically 2. Limits graphically 3. Limits at infinity 4. Asymptotes 5. Continuity 6. Intermediate value theorem 7. Differentiability 8. Limit definition of a derivative 9. Average rate of change (approximate slope) 10. Tangent lines 11. Derivatives rules and special functions 12. Chain Rule 13. Application of chain rule 14. Derivatives of generic functions using chain rule 15. Implicit differentiation 16. Related rates 17. Derivatives of inverses 18. Logarithmic differentiation 19. Determine function behavior (increasing, decreasing, concavity) given a function 20. Determine function behavior (increasing, decreasing, concavity) given a derivative graph 21. Interpret first and second derivative values in a table 22. Determining if tangent line approximations are over or under estimates 23. Finding critical points and determining if they are relative maximum, relative minimum, or neither 24. Second derivative test for relative maximum or minimum 25. Finding inflection points 26. Finding and justifying critical points from a derivative graph 27. Absolute maximum and minimum 28. Application of maximum and minimum 29. Motion derivatives 30. Vertical motion 31. Mean value theorem 32. Approximating area with rectangles and trapezoids given a function 33. Approximating area with rectangles and trapezoids given a table of values 34. Determining if area approximations are over or under estimates 35. Finding definite integrals graphically 36. Finding definite integrals using given integral values 37. Indefinite integrals with power rule or special derivatives 38. Integration with u-substitution 39. Evaluating definite integrals 40. Definite integrals with u-substitution 41. Solving initial value problems (separable differential equations) 42. Creating a slope field 43.
    [Show full text]
  • SUPPLEMENTARY MATERIAL: I. Fitting of the Hessian Matrix
    Supplementary Material (ESI) for PCCP This journal is © the Owner Societies 2010 1 SUPPLEMENTARY MATERIAL: I. Fitting of the Hessian matrix In the fitting of the Hessian matrix elements as functions of the reaction coordinate, one can take advantage of symmetry. The non-diagonal elements may be written in the form of numerical derivatives as E(Δα, Δβ ) − E(Δα,−Δβ ) − E(−Δα, Δβ ) + E(−Δα,−Δβ ) H (α, β ) = . (S1) 4δ 2 Here, α and β label any of the 15 atomic coordinates in {Cx, Cy, …, H4z}, E(Δα,Δβ) denotes the DFT energy of CH4 interacting with Ni(111) with a small displacement along α and β, and δ the small displacement used in the second order differencing. For example, the H(Cx,Cy) (or H(Cy,Cx)) is 0, since E(ΔCx ,ΔC y ) = E(ΔC x ,−ΔC y ) and E(−ΔCx ,ΔC y ) = E(−ΔCx ,−ΔC y ) . From Eq.S1, one can deduce the symmetry properties of H of methane interacting with Ni(111) in a geometry belonging to the Cs symmetry (Fig. 1 in the paper): (1) there are always 18 zero elements in the lower triangle of the Hessian matrix (see Fig. S1), (2) the main block matrices A, B and F (see Fig. S1) can be split up in six 3×3 sub-blocks, namely A1, A2 , B1, B2, F1 and F2, in which the absolute values of all the corresponding elements in the sub-blocks corresponding to each other are numerically identical to each other except for the sign of their off-diagonal elements, (3) the triangular matrices E1 and E2 are also numerically the same except for the sign of their off-diagonal terms, (4) the 1 Supplementary Material (ESI) for PCCP This journal is © the Owner Societies 2010 2 block D is a unique block and its off-diagonal terms differ only from each other in their sign.
    [Show full text]
  • EUCLIDEAN DISTANCE MATRIX COMPLETION PROBLEMS June 6
    EUCLIDEAN DISTANCE MATRIX COMPLETION PROBLEMS HAW-REN FANG∗ AND DIANNE P. O’LEARY† June 6, 2010 Abstract. A Euclidean distance matrix is one in which the (i, j) entry specifies the squared distance between particle i and particle j. Given a partially-specified symmetric matrix A with zero diagonal, the Euclidean distance matrix completion problem (EDMCP) is to determine the unspecified entries to make A a Euclidean distance matrix. We survey three different approaches to solving the EDMCP. We advocate expressing the EDMCP as a nonconvex optimization problem using the particle positions as variables and solving using a modified Newton or quasi-Newton method. To avoid local minima, we develop a randomized initial- ization technique that involves a nonlinear version of the classical multidimensional scaling, and a dimensionality relaxation scheme with optional weighting. Our experiments show that the method easily solves the artificial problems introduced by Mor´e and Wu. It also solves the 12 much more difficult protein fragment problems introduced by Hen- drickson, and the 6 larger protein problems introduced by Grooms, Lewis, and Trosset. Key words. distance geometry, Euclidean distance matrices, global optimization, dimensional- ity relaxation, modified Cholesky factorizations, molecular conformation AMS subject classifications. 49M15, 65K05, 90C26, 92E10 1. Introduction. Given the distances between each pair of n particles in Rr, n r, it is easy to determine the relative positions of the particles. In many applications,≥ though, we are given only some of the distances and we would like to determine the missing distances and thus the particle positions. We focus in this paper on algorithms to solve this distance completion problem.
    [Show full text]
  • Multivariable and Vector Calculus
    Multivariable and Vector Calculus Lecture Notes for MATH 0200 (Spring 2015) Frederick Tsz-Ho Fong Department of Mathematics Brown University Contents 1 Three-Dimensional Space ....................................5 1.1 Rectangular Coordinates in R3 5 1.2 Dot Product7 1.3 Cross Product9 1.4 Lines and Planes 11 1.5 Parametric Curves 13 2 Partial Differentiations ....................................... 19 2.1 Functions of Several Variables 19 2.2 Partial Derivatives 22 2.3 Chain Rule 26 2.4 Directional Derivatives 30 2.5 Tangent Planes 34 2.6 Local Extrema 36 2.7 Lagrange’s Multiplier 41 2.8 Optimizations 46 3 Multiple Integrations ........................................ 49 3.1 Double Integrals in Rectangular Coordinates 49 3.2 Fubini’s Theorem for General Regions 53 3.3 Double Integrals in Polar Coordinates 57 3.4 Triple Integrals in Rectangular Coordinates 62 3.5 Triple Integrals in Cylindrical Coordinates 67 3.6 Triple Integrals in Spherical Coordinates 70 4 Vector Calculus ............................................ 75 4.1 Vector Fields on R2 and R3 75 4.2 Line Integrals of Vector Fields 83 4.3 Conservative Vector Fields 88 4.4 Green’s Theorem 98 4.5 Parametric Surfaces 105 4.6 Stokes’ Theorem 120 4.7 Divergence Theorem 127 5 Topics in Physics and Engineering .......................... 133 5.1 Coulomb’s Law 133 5.2 Introduction to Maxwell’s Equations 137 5.3 Heat Diffusion 141 5.4 Dirac Delta Functions 144 1 — Three-Dimensional Space 1.1 Rectangular Coordinates in R3 Throughout the course, we will use an ordered triple (x, y, z) to represent a point in the three dimensional space.
    [Show full text]
  • Removing External Degrees of Freedom from Transition State
    Removing External Degrees of Freedom from Transition State Search Methods using Quaternions Marko Melander1,2*, Kari Laasonen1,2, Hannes Jónsson3,4 1) COMP Centre of Excellence, Aalto University, FI-00076 Aalto, Finland 2) Department of Chemistry, Aalto University, FI-00076 Aalto, Finland 3) Department of Applied Physics, Aalto University, FI-00076 Aalto, Finland 4) Faculty of Physical Sciences, University of Iceland, 107 Reykjavík, Iceland 1 ABSTRACT In finite systems, such as nanoparticles and gas-phase molecules, calculations of minimum energy paths (MEP) connecting initial and final states of transitions as well as searches for saddle points are complicated by the presence of external degrees of freedom, such as overall translation and rotation. A method based on quaternion algebra for removing the external degrees of freedom is described here and applied in calculations using two commonly used methods: the nudged elastic band (NEB) method for finding minimum energy paths and DIMER method for finding the minimum mode in minimum mode following searches of first order saddle points. With the quaternion approach, fewer images in the NEB are needed to represent MEPs accurately. In both NEB and DIMER calculations of finite systems, the number of iterations required to reach convergence is significantly reduced. The algorithms have been implemented in the Atomic Simulation Environment (ASE) open source software. Keywords: Nudged Elastic Band, DIMER, quaternion, saddle point, transition. 2 1. INTRODUCTION Chemical reactions, diffusion events and configurational changes of molecules are transitions from some initial arrangement of the atoms to another, from an initial state minimum on the energy surface to a final state minimum.
    [Show full text]
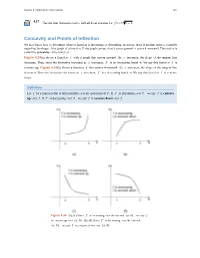
  • Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
    Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing.
    [Show full text]
  • Linear Algebra Review James Chuang
    Linear algebra review James Chuang December 15, 2016 Contents 2.1 vector-vector products ............................................... 1 2.2 matrix-vector products ............................................... 2 2.3 matrix-matrix products ............................................... 4 3.2 the transpose .................................................... 5 3.3 symmetric matrices ................................................. 5 3.4 the trace ....................................................... 6 3.5 norms ........................................................ 6 3.6 linear independence and rank ............................................ 7 3.7 the inverse ...................................................... 7 3.8 orthogonal matrices ................................................. 8 3.9 range and nullspace of a matrix ........................................... 8 3.10 the determinant ................................................... 9 3.11 quadratic forms and positive semidefinite matrices ................................ 10 3.12 eigenvalues and eigenvectors ........................................... 11 3.13 eigenvalues and eigenvectors of symmetric matrices ............................... 12 4.1 the gradient ..................................................... 13 4.2 the Hessian ..................................................... 14 4.3 gradients and hessians of linear and quadratic functions ............................. 15 4.5 gradients of the determinant ............................................ 16 4.6 eigenvalues
    [Show full text]
  • An Introduction to the HESSIAN
    An introduction to the HESSIAN 2nd Edition Photograph of Ludwig Otto Hesse (1811-1874), circa 1860 https://upload.wikimedia.org/wikipedia/commons/6/65/Ludwig_Otto_Hesse.jpg See page for author [Public domain], via Wikimedia Commons I. As the students of the first two years of mathematical analysis well know, the Wronskian, Jacobian and Hessian are the names of three determinants and matrixes, which were invented in the nineteenth century, to make life easy to the mathematicians and to provide nightmares to the students of mathematics. II. I don’t know how the Hessian came to the mind of Ludwig Otto Hesse (1811-1874), a quiet professor father of nine children, who was born in Koenigsberg (I think that Koenigsberg gave birth to a disproportionate 1 number of famous men). It is possible that he was studying the problem of finding maxima, minima and other anomalous points on a bi-dimensional surface. (An alternative hypothesis will be presented in section X. ) While pursuing such study, in one variable, one first looks for the points where the first derivative is zero (if it exists at all), and then examines the second derivative at each of those points, to find out its “quality”, whether it is a maximum, a minimum, or an inflection point. The variety of anomalies on a bi-dimensional surface is larger than for a one dimensional line, and one needs to employ more powerful mathematical instruments. Still, also in two dimensions one starts by looking for points where the two first partial derivatives, with respect to x and with respect to y respectively, exist and are both zero.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Linear Algebra Primer
    Linear Algebra Review Linear Algebra Primer Slides by Juan Carlos Niebles*, Ranjay Krishna* and Maxime Voisin *Stanford Vision and Learning Lab 27 - Sep - 2018 Another, very in-depth linear algebra review from CS229 is available here: http://cs229.stanford.edu/section/cs229-linalg.pdf And a video discussion of linear algebra from EE263 is here (lectures 3 and 4): https://see.stanford.edu/Course/EE263 1 Stanford University Outline Linear Algebra Review • Vectors and matrices – Basic Matrix Operations – Determinants, norms, trace – Special Matrices • Transformation Matrices – Homogeneous coordinates – Translation • Matrix inverse 27 - • Matrix rank Sep - • Eigenvalues and Eigenvectors 2018 • Matrix Calculus 2 Stanford University Outline Vectors and matrices are just Linear Algebra Review • Vectors and matrices collections of ordered numbers – Basic Matrix Operations that represent something: location in space, speed, pixel brightness, – Determinants, norms, trace etc. We’ll define some common – Special Matrices uses and standard operations on • Transformation Matrices them. – Homogeneous coordinates – Translation • Matrix inverse 27 - • Matrix rank Sep - • Eigenvalues and Eigenvectors 2018 • Matrix Calculus 3 Stanford University Vector Linear Algebra Review • A column vector where • A row vector where 27 - Sep - 2018 denotes the transpose operation 4 Stanford University Vector • We’ll default to column vectors in this class Linear Algebra Review 27 - Sep - • You’ll want to keep track of the orientation of your 2018 vectors when programming in python 5 Stanford University Some vectors have a geometric interpretation, others don’t… Linear Algebra Review • Other vectors don’t have a • Some vectors have a geometric interpretation: geometric – Vectors can represent any kind of interpretation: 27 data (pixels, gradients at an - – Points are just vectors image keypoint, etc) Sep - from the origin.
    [Show full text]
  • Matrix Calculus
    Appendix D Matrix Calculus From too much study, and from extreme passion, cometh madnesse. Isaac Newton [205, §5] − D.1 Gradient, Directional derivative, Taylor series D.1.1 Gradients Gradient of a differentiable real function f(x) : RK R with respect to its vector argument is defined uniquely in terms of partial derivatives→ ∂f(x) ∂x1 ∂f(x) , ∂x2 RK f(x) . (2053) ∇ . ∈ . ∂f(x) ∂xK while the second-order gradient of the twice differentiable real function with respect to its vector argument is traditionally called the Hessian; 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂x1 ∂x1∂x2 ··· ∂x1∂xK 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 2 K f(x) , ∂x2∂x1 ∂x2 ··· ∂x2∂xK S (2054) ∇ . ∈ . .. 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂xK ∂x1 ∂xK ∂x2 ∂x ··· K interpreted ∂f(x) ∂f(x) 2 ∂ ∂ 2 ∂ f(x) ∂x1 ∂x2 ∂ f(x) = = = (2055) ∂x1∂x2 ³∂x2 ´ ³∂x1 ´ ∂x2∂x1 Dattorro, Convex Optimization Euclidean Distance Geometry, Mεβoo, 2005, v2020.02.29. 599 600 APPENDIX D. MATRIX CALCULUS The gradient of vector-valued function v(x) : R RN on real domain is a row vector → v(x) , ∂v1(x) ∂v2(x) ∂vN (x) RN (2056) ∇ ∂x ∂x ··· ∂x ∈ h i while the second-order gradient is 2 2 2 2 , ∂ v1(x) ∂ v2(x) ∂ vN (x) RN v(x) 2 2 2 (2057) ∇ ∂x ∂x ··· ∂x ∈ h i Gradient of vector-valued function h(x) : RK RN on vector domain is → ∂h1(x) ∂h2(x) ∂hN (x) ∂x1 ∂x1 ··· ∂x1 ∂h1(x) ∂h2(x) ∂hN (x) h(x) , ∂x2 ∂x2 ··· ∂x2 ∇ .
    [Show full text]