World's Smallest Electric Brain
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Please Be Aware That This Play Is Fully Potected by Copyright
1 PLEASE BE AWARE THAT THIS PLAY IS FULLY POTECTED BY COPYRIGHT All plays, books, music and other materials published by Heartland Plays, Inc. are fully protected under the copyright laws of the United States of America and all countries which the United States has reciprocal relations including, but not limited to all countries covered by the Pan-American Copyright Convention, The Universal Copyright Convention and the Berne Convention. All rights to the plays and materials on our website are strictly reserved including, and without limitation, professional and amateur performance rights; motion pictures; public reading; radio and television broadcasting; audio and video recording and reproduction of any type known or yet to be invented; information storage and retrieval systems of any type known or yet to be invented; and the rights of translation into any and all languages. No individual or organization whether amateur or stock may perform this or any play published by Heartland Plays, Inc. without first obtaining advance permission from Heartland Plays, Inc. and paying the appropriate fees including Royalties and Single-Use Copyright fees. Heartland Plays, Inc. collects royalties on behalf of the Playwrights whose plays it publishes. Unauthorized copying, transcribing or reproduction of this or any play or excerpt, or storage or transmittal in any form and by any means whether known or yet to be invented, is strictly forbidden except as provided by Agreement with Heartland Plays, Inc. Any unauthorized use is a violation of copyright laws and will be prosecuted to the fullest extent of the law. FIVE SIMPLE RULES TO REMEMBER 1. -

February, 1931
FEBRUARY, 1931 PRINTED AT BERLIN, N. H., U. LOUVILLE B. PAINE BROWN BULLETIN • Louville B. Paine, an employee of the PRINTED UPON NIBROC S U P E R C A L E N D E R E D BOND Sulphite Mill, and a prominent and highly respected citizen of Berlin, passed away at his home on Church Street on Febru- Vol. XIII. FEBRUARY, 1931 No. 8 ary 4, following a brief illness of pneu- monia. He was born in Milan 68 years BROWN BULLETIN PUBLISHING ASSOCIATION ago, the son of Gardner D. Paine and "The object of this organization is to publish a paper for the benefit of the employees of the Brown Company and of the Brown Corporation in which may appear items of local and general interest; and Susan Bracket Paine. The family moved which will tend to further the cause of co-operation, progress and friendliness among and between all to Berlin when Mr. Paine was a very sections of these companies."—By-Laws, Article 2. young child. His father was one of the pioneer business men of Berlin. EDITORIAL STAFF Mr. Paine was an associate editor of Editor—J. M. McGivney Photographic Editor—Victor Beaudoin the Brown Bulletin, and his numerous Associate Editors-Louville Paine, C. H. Cartoonist-Alfred Laflamme articles, depicting the lives of interesting Mott. and John Hayward & Editor-Robert Murphy Assistant Editors—John Heck, Paul characters in this section during the past Grenier, Kenneth Harvey 60 years, and outstanding events in the early history of Berlin, were always high- ly entertaining and instructive. -

Cats Adorn Polish Stamps
feline infectious enteritis vaccine for the protection Feline infectious enteritis is a highly infectious and dangerous disease of cats: it kills 9 out of 10 of those that contract it. Treatment is usually unsuccessful. The best protection against this dreadful disease is vaccination with FEV. Choose a time when your cat is fit and healthy then ask your veterinary surgeon about protection with FEV feline infectious enteritis vaccine. BEBRINGWERKE AG. FEV protects your cat ",,"aUIO·LAKN 13. ~~ HOECHST PHARMACEUTICALS LTD., Veterinary Division Portland House, Stag Place, Victoria, London, S.W.1 VOL. 17 No.3 MCau MARCH 1965 lUTHORITATIVE • INSTRUCTIVE· ENTERTAINING Published every ""ootb with tbe beet po••i. ble features and illustration. and circulated Managing Editor: to Cat Lovers of every kind throughout tbe world. Our editorial purpose is : ARTHUR E. COWLISHAW (I) to spread a wider understanding aDd a -4 CARLTON MANSIONS berter appreciation of all cats, their care and CLAPHAM ROAD. LONDON. S.W.9 mana~em.ent; (2) to encourage in every way the bre"din&. handlinfl: and sbowing oC pedigree cats; (3) to work for the 8uppre••ioD ofevery forDJ Australian and New Zealand oC cruelty to cats ; Correspondent: (4) to act as .liok of friend$bip aDd coaUbon interest between cal lover. in different part_ MR. F. W. ~EARCE. II OLD BEROWRA of the world. ROAD,HORNSBY,N.S.W.• AUSTRALIA THE MAGAZINE THAT SPANS THE WORLD OF CAT LOVERS INTERNATIONAL CHAMPION BENTVELD HONEYCOMB. lovely CreaDl female by Cb. Bentveld Bronx Cocktail and Bentveld Meftlory. Bred by the well known DUICh Caneier M.iss PosthuDla, Hofte-ycornb now belons. -
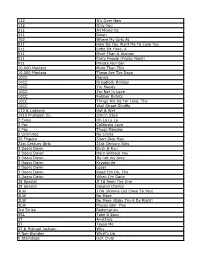
112 It's Over Now 112 Only You 311 All Mixed up 311 Down
112 It's Over Now 112 Only You 311 All Mixed Up 311 Down 702 Where My Girls At 911 How Do You Want Me To Love You 911 Little Bit More, A 911 More Than A Woman 911 Party People (Friday Night) 911 Private Number 10,000 Maniacs More Than This 10,000 Maniacs These Are The Days 10CC Donna 10CC Dreadlock Holiday 10CC I'm Mandy 10CC I'm Not In Love 10CC Rubber Bullets 10CC Things We Do For Love, The 10CC Wall Street Shuffle 112 & Ludacris Hot & Wet 1910 Fruitgum Co. Simon Says 2 Evisa Oh La La La 2 Pac California Love 2 Pac Thugz Mansion 2 Unlimited No Limits 20 Fingers Short Dick Man 21st Century Girls 21st Century Girls 3 Doors Down Duck & Run 3 Doors Down Here Without You 3 Doors Down Its not my time 3 Doors Down Kryptonite 3 Doors Down Loser 3 Doors Down Road I'm On, The 3 Doors Down When I'm Gone 38 Special If I'd Been The One 38 Special Second Chance 3LW I Do (Wanna Get Close To You) 3LW No More 3LW No More (Baby I'm A Do Right) 3LW Playas Gon' Play 3rd Strike Redemption 3SL Take It Easy 3T Anything 3T Tease Me 3T & Michael Jackson Why 4 Non Blondes What's Up 5 Stairsteps Ooh Child 50 Cent Disco Inferno 50 Cent If I Can't 50 Cent In Da Club 50 Cent In Da Club 50 Cent P.I.M.P. (Radio Version) 50 Cent Wanksta 50 Cent & Eminem Patiently Waiting 50 Cent & Nate Dogg 21 Questions 5th Dimension Aquarius_Let the sunshine inB 5th Dimension One less Bell to answer 5th Dimension Stoned Soul Picnic 5th Dimension Up Up & Away 5th Dimension Wedding Blue Bells 5th Dimension, The Last Night I Didn't Get To Sleep At All 69 Boys Tootsie Roll 8 Stops 7 Question -

The Kpatience Handbook
The KPatience Handbook Paul Olav Tvete Maren Pakura Stephan Kulow Reviewer: Mike McBride Developer: Paul Olav Tvete Developer: Stephan Kulow The KPatience Handbook 2 Contents 1 Introduction 5 2 How to Play 6 3 Game Rules, Strategies and Tips7 3.1 General Rules . .7 3.2 Rules for Individual Games . .8 3.2.1 Klondike . .8 3.2.2 Grandfather . .9 3.2.3 Aces Up . .9 3.2.4 Freecell . 10 3.2.5 Mod3 . 10 3.2.6 Gypsy . 11 3.2.7 Forty & Eight . 11 3.2.8 Simple Simon . 11 3.2.9 Yukon . 11 3.2.10 Grandfather’s Clock . 12 3.2.11 Golf . 12 3.2.12 Spider . 12 3.2.13 Baker’s Dozen . 12 3.2.14 Castle . 13 4 Interface Overview 14 4.1 The Game Menu . 14 4.2 The Move Menu . 15 4.3 The Settings and Help Menu . 15 5 Frequently asked questions 17 6 Credits and License 18 7 Index 19 Abstract This documentation describes the game of KPatience version 21.04 The KPatience Handbook Chapter 1 Introduction GAMETYPE: Card NUMBER OF POSSIBLE PLAYERS: One To play patience you need, as the name suggests, patience. For simple games, where the way the game goes depends only upon how the cards fall, your patience might be the only thing you need. There are also patience games where you must plan your strategy and think ahead in order to win. A theme common to all the games is the player must put the cards in a special order — moving, turning and reordering them. -

The Dictionary Legend
THE DICTIONARY The following list is a compilation of words and phrases that have been taken from a variety of sources that are utilized in the research and following of Street Gangs and Security Threat Groups. The information that is contained here is the most accurate and current that is presently available. If you are a recipient of this book, you are asked to review it and comment on its usefulness. If you have something that you feel should be included, please submit it so it may be added to future updates. Please note: the information here is to be used as an aid in the interpretation of Street Gangs and Security Threat Groups communication. Words and meanings change constantly. Compiled by the Woodman State Jail, Security Threat Group Office, and from information obtained from, but not limited to, the following: a) Texas Attorney General conference, October 1999 and 2003 b) Texas Department of Criminal Justice - Security Threat Group Officers c) California Department of Corrections d) Sacramento Intelligence Unit LEGEND: BOLD TYPE: Term or Phrase being used (Parenthesis): Used to show the possible origin of the term Meaning: Possible interpretation of the term PLEASE USE EXTREME CARE AND CAUTION IN THE DISPLAY AND USE OF THIS BOOK. DO NOT LEAVE IT WHERE IT CAN BE LOCATED, ACCESSED OR UTILIZED BY ANY UNAUTHORIZED PERSON. Revised: 25 August 2004 1 TABLE OF CONTENTS A: Pages 3-9 O: Pages 100-104 B: Pages 10-22 P: Pages 104-114 C: Pages 22-40 Q: Pages 114-115 D: Pages 40-46 R: Pages 115-122 E: Pages 46-51 S: Pages 122-136 F: Pages 51-58 T: Pages 136-146 G: Pages 58-64 U: Pages 146-148 H: Pages 64-70 V: Pages 148-150 I: Pages 70-73 W: Pages 150-155 J: Pages 73-76 X: Page 155 K: Pages 76-80 Y: Pages 155-156 L: Pages 80-87 Z: Page 157 M: Pages 87-96 #s: Pages 157-168 N: Pages 96-100 COMMENTS: When this “Dictionary” was first started, it was done primarily as an aid for the Security Threat Group Officers in the Texas Department of Criminal Justice (TDCJ). -

A 16 Bar Cut: the History of American Musical Theatrean Original Script and Monograph Document
University of Central Florida STARS Electronic Theses and Dissertations, 2004-2019 2006 A 16 Bar Cut: The History Of American Musical Theatrean Original Script And Monograph Document Patrick Moran University of Central Florida Part of the Theatre and Performance Studies Commons Find similar works at: https://stars.library.ucf.edu/etd University of Central Florida Libraries http://library.ucf.edu This Masters Thesis (Open Access) is brought to you for free and open access by STARS. It has been accepted for inclusion in Electronic Theses and Dissertations, 2004-2019 by an authorized administrator of STARS. For more information, please contact [email protected]. STARS Citation Moran, Patrick, "A 16 Bar Cut: The History Of American Musical Theatrean Original Script And Monograph Document" (2006). Electronic Theses and Dissertations, 2004-2019. 916. https://stars.library.ucf.edu/etd/916 A 16 BAR CUT: THE HISTORY OF AMERICAN MUSICAL THEATRE An Original Script and Monograph Document by PATRICK JOHN MORAN B.A. Greensboro College, 2003 A thesis submitted in partial fulfillment of the requirements for the degree of Master of Fine Arts in the Department of Theatre in the College of Arts and Humanities at the University of Central Florida Orlando, Florida Summer Term 2006 © 2006 Patrick John Moran ii ABSTRACT A final thesis for my Master of Fine Arts degree should encompass every aspect of the past few years spent in the class room. Therefore, as a perfect capstone to my degree, I have decided to conceive, write, and perform a new musical with my classmate Rockford Sansom entitled The History of Musical Theatre: A 16 Bar Cut. -

Nursery Rhymes
NURSERY RHYMES A Apple Pie. A. Apple Pie. London: Frederick Warne & Co.,[ca 1865] 26.8 x 22.6 cm. pub yellow col pict wraps; folder (Aunt Louisa's London Toy Books) Three Centuries 605. Imperfect: rear wrapper wanting. Colophon of Kronheim & Co at foot of front wrapper Opie N 1 A Apple Pie. The Apple Pie. [London: Darton & Co., 58 Holborn Hill, (not after 1860)] 25 x 17 cm. pub orange col pict wraps with ads on rear; folder (Darton's Indestructible Elementary Children's Books) Three Centuries 603. Inscription dated 8 February 1860; second set of wrappers pasted down as endpapers Opie N 2 A Apple Pie. The Apple-Pie Alphabet. Derby: John and Charles Mozley, 6 Paternoster Row, London [between 1851 and 1874] 13.2 x 8.1 cm. pub yellow pict wraps with list of one-penny chapbooks on rear; folder Three Centuries 601. This title listed as number 26 in the ad on the rear. Colophon of John and Charles Mozley, Derby Opie N 580 A Apple Pie. The Apple-Pie Alphabet. London: John and Charles Mozley, 6 Paternoster Row, [between 1851 and 1874] 13.1 x 8.2 cm. pub yellow pict wraps with poem on rear; folder Three Centuries 601. Colophon of Henry Mozley and Sons, Derby; signature on front wrap. This title number 26 in the publisher's series of penny chapbooks Opie N 581 A Apple Pie. A Apple Pie. An Alphabet from Modelled Designs by Mrs. Wm. Harbutt. Pen and Ink Drawings by Noel C. Harbutt A.R.C.A. -

Grafik-Praktikum Beim Wildwechsel!
U1_Titel_316_sued.indd u1 23.02.2016 07:19:46 Nacht der Bewerber 2016 Ausbildungsmesse mit Eventcharakter 29. April 2016 Kirchhain Beginn 18:30 Uhr Ende 22:30 Uhr Das erwartet euch: 3 über 40 Ausbildungsbetriebe 3 über 100 Ausbildungsberufe 3 Friseur, Make-Up & Fotograf für das perfekte Bewerbungsfoto 3 DJ, Cocktails, Snacks und vieles mehr Jetzt gleich online anmelden: www.nacht-der-bewerber.info MEHR als AUSBILDUNG U2_316_Sued.indd u2 23.02.2016 08:23:15 |Vorspiel|+ „Nimm dir Zeit, um froh zu sein – denn es ist die Gesucht: Musik der Seele“ Redaktions-Praktikant/in irischer Segenswunsch Bewerbungen an: [email protected] Im katholischen Irland selbst wird dieser Tag im Familienkreis eher ruhig gefeiert. Zu der Alles im grüneng großen SauseSause,, aals die der St. Pa- trickstricks DDayay heutehe bekannt ist, Bereich! hhabenaben ihn ddie irischen Emi- ggrantenranten iinn den USA ge- m 17. März mmacht.acht. Zum ersten Mal Wer wagt, gewinnt! ist die gan- fafandnd eine P arade Na, wen haben wir denn hier beim A ze Welt grün. 1843188 in Chica go Wildwechseln erwischt? Der St. Patrick‘s Dayay mmit ca. 800 Teil- >> Schreib uns eine Mail (Btr: wwvip) (irisch: Lá Fhéile Pádra-dra- nehmern statt. an [email protected] mit der ig) wird gefeiert und übüberer Allerdings ist Lösung (z.B.: wwvip Heino)! die ganze Welt verteilteeilt werden der schiere Grö- Vielleicht gewinnt ihr was Schönes! Flüsse grün gefärbt,tt, Menschen ßenunterschied kleiden sich grün, selbstelbst das Bier nnicht verwun- >> Richtig! wird grün gefärbt. AberAAber um was dderlich,erlicc leben in den In 02/16 hatten wir DJ geht es dabei eigentlich?ttlich? UUSASA doch mehmehrr irischstämmige Newman geblitzdingst. -
At Tf\Fl Ser1jice of Depauw the Citizens Trust Company .--DREW- Has the Largest Faculty of Any Theological School in Methodism
THE D E P AU \V M AGAZl l'\E The literary publication of DePauw University, Greencastle. Indiana. [ssuecl in the months of October. Decemher. \hrch, and May. Entered as second-class matter );'ovember 13. 1919, at the post office at Gr eencastle. Indiana. untlcr th t;> Act of ~~ arch 3, I 79. Yearly suiJscription SI.OO: :.in~le copies 35 cents. 1: /)I T 0 R S I· r ,,, llnr CFoRr." ::.~wc~o. E\111,\' M .\RI:->r. I I H.!' 'I Til AI. KEllY \lAkY P••R'f£R 1 ~1.11 \I\! Ill Tll.ll' \; 1{. \\'. PE~C£, .\fa110gi~rg Edllor F•11 IIRI ''· ~T \t'l' Jaml<> llrll. Jnhn Hruhn , l.y man ('Jp~·. \ tr ~11!1,1 l'nttinAharn, L e~t<·r Dolk, \ itwr \ ~n·ularh, Elmer l~u,taf ... ,,n, CedriC' Gran. Eli?ahrth llau~<.. j 11hn Lo •ckwt•od, l\l.rrgan•t \hey. Flmcncc ~1 di;w~he). Margaret r Mc l~;lllglH•), Dclore~ \!cib, I mngenc M u l ltn~. J an('t K efi, William Ongc, Josephine Overton, Bower Pennington, Mary Eli1ahcth Plummer. ll elcn Preston. Loui!'C? Quinn. Elranor Rauh. Alice Reeves. Doris Smith. (~. Herhert Smith. Nilln Stall, Richard \\'ad t>l. Volume VI MAY, 1925 Number 4 CONTENTS Belter Fi!ty Years of Henry .... Esther Greenwood F elt 3 Crossing the Rubicon .............. Annabelle McWethy 15 Listen ................................................... Portia Showalter 17 History Revised ............................ George B. Manhart 18 Poems . .... .. .. ............... .... ....... Lester Dolk 22 On Taking Note ~; . .................... Virginia Cottingham 23 Snow In April .. ........... .. ........ Ruth H. Troulmnn 24 Announcements 24 The Book Nook 25 Our Contributors Miss Esther Felt, winner of the Doubleday-Page--0. -

Health - DNA Test Report: DNA - PRA (Cord1)
Health - DNA Test Report: DNA - PRA (cord1) Hound - Dachshund (Miniature Smooth Haired) Dog Name Reg No DOB Sex Sire Dam Test Date Test Result A DASH OF SILVER AV03504902 19/08/2018 Bitch TRACYZDAX CHOCCHEEKYCHAP QUEEN LATIFA 09/10/2018 Carrier AAH MAISIES DAISY GRACE AP00571501 07/12/2011 Bitch BLACK PASSION OF DONNADOON ROIJUL BRACKENS EARLY DAWN 13/05/2014 Clear ABBAGIRLS CRUNCHY NUT AJ00196101 06/11/2007 Bitch BILBO BOSS FOR WELCUMEN ABBAGIRLS INAD-INAD 19/06/2012 Clear ABBAGIRLS HI BURY FOR WELCUMEN AJ00809705 24/12/2007 Bitch BILBO BOSS FOR WELCUMEN BRONIA LA LUCIDA AT ABBAGIRLS 26/02/2009 Carrier ABBAGIRLS WAY OUT WEST AJ03373902 17/06/2008 Bitch BILBO BOSS FOR WELCUMEN ABBAGIRLS MOE-MOE 23/05/2011 Carrier ABBAGIRLS WEETABIX AJ00196105 06/11/2007 Bitch BILBO BOSS FOR WELCUMEN ABBAGIRLS INAD-INAD 02/12/2009 Clear ABBEY ROYAL MIST AV04880503 23/08/2018 Bitch BEAGISBEANAN KHAL DROGO PRINCESS ROSE (IKC) 03/03/2020 Clear ABBEYDAC INUSFRE AM04565201 02/11/2011 Dog CALERICA SEE THE STARS DOVESTREAM XOTIC DREAM AT 16/01/2012 Carrier ABBEYDAC ABBEYDAC LIFFIE AM04565203 02/11/2011 Bitch CALERICA SEE THE STARS DOVESTREAM XOTIC DREAM AT 16/01/2012 Carrier ABBEYDAC ABBEYDAC MY GINUS AM04565202 02/11/2011 Bitch CALERICA SEE THE STARS DOVESTREAM XOTIC DREAM AT 16/01/2012 Carrier ABBEYDAC ABBEYDAC SHANNON AT DOVESTREAM AM04565204 02/11/2011 Bitch CALERICA SEE THE STARS DOVESTREAM XOTIC DREAM AT 16/01/2012 Clear ABBEYDAC ABBEYVIEW MARTHA AW03864801 10/10/2019 Bitch CACAO SOUFFLE VIA ARBENNIK SUZIE SUGAR 11/05/2020 Clear ABDISALAM AATO AR04000601 -

Dot Re Dame Scholastic • DI5CE• QV/ASI • SEMPER-VICTURV/S- -VIVE- QV/ASI • CRA5 • M0RIT\/RV5 • •F-X'a
Dot re Dame Scholastic • DI5CE• QV/ASI • SEMPER-VICTURV/S- -VIVE- QV/ASI • CRA5 • M0RIT\/RV5 • •F-X'A- VOL. XLI. NOTRE DAME, INDIANA, APEIL 25, 1908. No. 2S: sin, which were then most prevalent. A Weak Man. momentous period in history had been reached. Good contended against evil. To THOMAS A. LAHBY, '11. which side would the tide turn? That rested entirely with those concerned in STOOD loeside a lo^ pyramid, choosing a successor to the late incumbent I And gazed in awe upon the massive mount of Peter's chair. And who can estimate the Of solid rock, whose time-defying crest, Upreared into the clouds, still stands to count sagacity exhibited by all Christendom as The flight of ages numberless. And long she fixed her gaze upon a humble, monk, and I viewed that monument of human skill, hailed as Peter's successor one w^ho had So vast and huge in its entirety, been private counsellor to not less than five Until in wonderment, my soul athrill popes, and had frequently acted as papal With conscious pride upwelling in my heart, legate on the most complicated missions; I thought, "0 man, how like a god thou art!." hailed him as the one designed by the I gazed upon the Himalayan chain. Almighty to wage, among clergy and laity- That huge, stuj)endous bulk uptowering high, alike, that war of reform so manifestly Its hoar)--, element-emjjattled brow imperative ? Hildebrand was the man, the Above the very clouds that deck the sky; I rode three hundred leagues along its base.