DOCSLIB.ORG

A Text-Book of General Astronomy for Colleges and Scientific Schools

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Project Gutenberg's A Textbook of General Astronomy, by Charles A. Young This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.net Title: A Textbook of General Astronomy For Colleges and Scientific Schools Author: Charles A. Young Release Date: August 30, 2011 [EBook #37275] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK A TEXTBOOK OF GENERAL ASTRONOMY *** Produced by Susan Skinner, Nigel Blower, Brenda Lewis and the Online Distributed Proofreading Team at http://www.pgdp.net (This file was produced from images generously made available by the Biblioth`equenationale de France (BnF/Gallica) at http://gallica.bnf.fr, illustrations generously made available by The Internet Archive/Canadian Libraries) Transcriber's Notes A small number of minor typographical errors and inconsistencies have been corrected. See the DPtypo command in the LATEX source for more information. FRONTISPIECE. The Great Telescope of the Lick Observatory, Mt. Hamilton, Cal. Object-Glass made by A. Clark & Sons: Aperture, 36 in.; Focal Length, 56 ft. 2 in. Mounting by Warner & Swasey. ATEXT-BOOK OF GENERAL ASTRONOMY FOR COLLEGES AND SCIENTIFIC SCHOOLS BY CHARLES A. YOUNG, Ph.D., LL.D., Professor of Astronomy in the College of New Jersey (Princeton). Boston, U.S.A., and London: GINN & COMPANY, PUBLISHERS. 1889. Entered at Stationers' Hall. Copyright, 1888, by CHARLES A. YOUNG, All Rights Reserved. Typography by J. S. Cushing & Co., Boston, U.S.A. Presswork by Ginn & Co., Boston, U.S.A. PREFACE. The present work is designed as a text-book of Astronomy suited to the general course in our colleges and schools of science, and is meant to supply that amount of information upon the subject which may fairly be expected of every \liberally educated" person. While it assumes the previous discipline and mental maturity usu- ally corresponding to the latter years of the college course, it does not demand the peculiar mathematical training and aptitude nec- essary as the basis of a special course in the science|only the most elementary knowledge of Algebra, Geometry, and Trigonometry is required for its reading. Its aim is to give a clear, accurate, and justly proportioned presentation of astronomical facts, principles, and methods in such a form that they can be easily apprehended by the average college student with a reasonable amount of effort. The limitations of time are such in our college course that proba- bly it will not be possible in most cases for a class to take thoroughly everything in the book. The fine print is to be regarded rather as collateral reading, important to anything like a complete view of the subject, but not essential to the course. Some of the chapters can even be omitted in cases where it is found necessary to abridge the course as much as possible; e.g., the chapters on Instruments and on Perturbations. While the work is no mere compilation, it makes no claims to special originality: information and help have been drawn from all available sources. The author is under great obligations to the astronomical histories of Grant and Wolf, and especially to Miss Clerke's admirable \History of Astronomy in the Nineteenth Cen- tury." Many data also have been drawn from Houzeau's valuable \Vade Mecum de l'Astronomie." It has been intended to bring the book well down to date, and to indicate to the student the sources of information on subjects which are necessarily here treated inadequately on account of the PREFACE. v limitations of time and space. Special acknowledgments are due to Professor Langley and to his publishers, Messrs. Ticknor & Co., for the use of a number of illustrations from his beautiful book, \The New Astronomy"; and also to D. Appleton & Co. for the use of several cuts from the au- thor's little book on the Sun. Professor Trowbridge of Cambridge kindly provided the original negative from which was made the cut illustrating the comparison of the spectrum of iron with that of the sun. Warner & Swasey of Cleveland and Fauth & Co. of Washing- ton have also furnished the engravings of a number of astronomical instruments. Professors Todd, Emerson, Upton, and McNeill have given most valuable assistance and suggestions in the revision of the proof; as indeed, in hardly a less degree, have several others. The author will consider it a great favor if those who may use the book will kindly communicate to him, either directly or through the publishers, any errata, in order that they may be promptly corrected. Princeton, N. J., August, 1888. Note. In this issue of the book a number of errors which appeared in the first impression have been corrected. April, 1889. TABLE OF CONTENTS. PAGES INTRODUCTION . 1{4 CHAPTER I.|The Doctrine of the Sphere; Definitions and General Considerations . 5{20 CHAPTER II.|Astronomical Instruments: the Telescope; Time-Keepers and Chronograph; the Transit Instrument and Accessories; the Meridian Circle and Reading Mi- croscope; the Altitude and Azimuth Instrument; the Equatorial Instrument and Micrometer; the Sextant . 21{58 CHAPTER III.|Corrections to Astronomical Observa- tions: the Dip of the Horizon; Parallax; Semi-Diameter; Refraction; and Twilight . 59{71 CHAPTER IV.|Problems of Practical Astronomy: the Determination of Latitude, of Time, of Longitude, of a Ship's Place at Sea, of Azimuth, and of the Apparent Right Ascension and Declination of a Heavenly Body; the Time of Sunrise or Sunset . 72{93 CHAPTER V.|The Earth: the Approximate Determination of its Dimensions and Form; Proofs of its Rotation; Accurate Determination of its Dimensions by Geodetic Surveys and Pendulum Observations; Determination of its Mass and Density . 94{120 CHAPTER VI.|The Earth's Orbital Motion: the Motion of the Sun among the Stars; the Equation of Time; Precession; Nutation; Aberration; the Calendar . 121{148 CHAPTER VII.|The Moon: her Orbital Motion; Distance and Dimensions; Mass, Density, and Superficial Gravity; Rotation and Librations; Phases; Light and Heat; Physical Condition; Influence exerted on the Earth; Surface Structure; and Possible Changes . 149{176 TABLE OF CONTENTS. vii PAGES CHAPTER VIII.|The Sun: Distance and Dimensions; Mass and Density; Rotation; Solar Eye-Pieces, and Study of the Sun's Surface; General Views as to Constitution; Sun Spots: their Appearance, Nature, Distribution, and Periodicity; the Spectroscope and the Solar Spectrum; Chemical Composition of the Sun; the Chromosphere and Prominences; the Corona . 177{216 CHAPTER IX.|The Sun's Light and Heat: Comparison of Sunlight with Artificial Lights; the Measurement of the Sun's Heat, and Determination of the Solar Constant; the Pyrheliometer, Actinometer, and Bolometer; the Sun's Temperature; Maintenance of the Sun's Radiation; and Conclusions as to its Age and Future Endurance . 217{232 CHAPTER X.|Eclipses; Form and Dimensions of Shadows; Lunar Eclipses; Solar Eclipses, Total, Annular, and Partial; Ecliptic Limits, and Number of Eclipses in a Year; the Saros; Occultations . 233{251 CHAPTER XI.|Central Forces; Equable Description of Areas; Areal, Linear, and Angular Velocities; Kepler's Laws and Inferences from them; Gravitation demonstrated by the Moon's Motion; Conic Sections as Orbits; the Problem of Two Bodies; the \Velocity from Infinity" and its Relation to the Species of Orbit described by a Body moving under Gravitation; Intensity of Gravitation . 252{273 CHAPTER XII.|The Problem of Three Bodies; Disturb- ing Forces; Lunar Perturbations and the Tides . 274{299 CHAPTER XIII.|The Planets: their Motions, Appar- ent and Real; the Ptolemaic, Tychonic, and Copernican Systems; the Orbits and their Elements; Planetary Perturbations . 300{322 CHAPTER XIV.|The Planets themselves; Methods of determining their Diameters, Masses, Densities, Times of Rotation, etc.; the \Terrestrial Planets,"|Mercury, Venus, and Mars; the Asteroids; Intra-Mercurial Planets and the Zodiacal Light . 323{355 CHAPTER XV.|The Major Planets,|Jupiter, Saturn, Uranus, and Neptune . 356{383 TABLE OF CONTENTS. viii PAGES CHAPTER XVI.|The Determination of the Sun's Hor- izontal Parallax and Distance; Oppositions of Mars and Transits of Venus; Gravitational Methods; Determi- nation by Means of the Velocity of Light . 384{402 CHAPTER XVII.|Comets: their Number, Motions, and Orbits; their Constituent Parts and Appearance; their Spectra, Physical Constitution, and Probable Origin . 403{438 CHAPTER XVIII.|Meteors: Aerolites, their Fall and Physical Characteristics; Shooting Stars and Meteoric Showers; Connection between Meteors and Comets . 439{455 CHAPTER XIX.|The Stars: their Nature and Number; the Constellations; Star-Catalogues; Designation of Stars; their Proper Motions, and the Motion of the Sun in Space; Stellar Parallax . 456{476 CHAPTER XX.|The Light of the Stars; Star Magni- tudes and Photometry; Variable Stars; Stellar Spectra; Scintillation of the Stars . 477{503 CHAPTER XXI.|Aggregations of Stars: Double and Multiple Stars; Clusters; Nebulæ; the Milky Way, and Distribution of Stars in Space; Constitution of the Stellar Universe; Cosmogony and the Nebular Hypothesis . 504{539 APPENDIX.|Tables of Astronomical Data . 540{547 INDEX . 548{567 INTRODUCTION. 1. Astronomy (ἄστροn nomoc´ ) is the science which treats of the heavenly bodies. As such bodies we reckon the sun and moon, the planets (of which the earth is one) and their satellites, comets and meteors, and finally the stars and nebulæ. We have to consider in Astronomy:| (a) The motions of these bodies, both real and apparent, and the laws which govern these motions. (b) Their forms, dimensions, and masses. (c) Their nature and constitution. (d) The effects they produce upon each other by their attrac- tions, radiations, or by any other ascertainable influence. It was an early, and has been a most persistent, belief that the heavenly bodies have a powerful influence upon human affairs, so that from a knowledge of their positions and \aspects" at critical moments (as for instance at the time of a person's birth) one could draw up a \horoscope" which would indicate the probable future.
Recommended publications
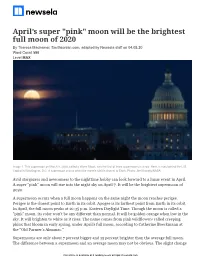
  • April's Super "Pink" Moon Will Be the Brightest Full Moon of 2020

    April's Super "Pink" Moon Will Be the Brightest Full Moon of 2020

    April’s super "pink" moon will be the brightest full moon of 2020 By Theresa Machemer, Smithsonian.com, adapted by Newsela staff on 04.05.20 Word Count 590 Level MAX Image 1. This supermoon on March 9, 2020, called a Worm Moon, was the first of three supermoons in a row. Here, it rises behind the U.S. Capitol in Washington, D.C. A supermoon occurs when the moon's orbit is closest to Earth. Photo: Joel Kowsky/NASA Avid stargazers and newcomers to the nighttime hobby can look forward to a lunar event in April. A super "pink" moon will rise into the night sky on April 7. It will be the brightest supermoon of 2020. A supermoon occurs when a full moon happens on the same night the moon reaches perigee. Perigee is the closest point to Earth in its orbit. Apogee is its farthest point from Earth in its orbit. In April, the full moon peaks at 10:35 p.m. Eastern Daylight Time. Though the moon is called a "pink" moon, its color won't be any different than normal. It will be golden orange when low in the sky. It will brighten to white as it rises. The name comes from pink wildflowers called creeping phlox that bloom in early spring, under April's full moon, according to Catherine Boeckmann at the "Old Farmer's Almanac." Supermoons are only about 7 percent bigger and 15 percent brighter than the average full moon. The difference between a supermoon and an average moon may not be obvious.
  • Book Self-Publishing Best Practices

    Book Self-Publishing Best Practices

    Montana Tech Library Digital Commons @ Montana Tech Graduate Theses & Non-Theses Student Scholarship Fall 2019 Book Self-Publishing Best Practices Erica Jansma Follow this and additional works at: https://digitalcommons.mtech.edu/grad_rsch Part of the Communication Commons Book Self-Publishing Best Practices by Erica Jansma A project submitted in partial fulfillment of the requirements for the degree of M.S. Technical Communication Montana Tech 2019 ii Abstract I have taken a manuscript through the book publishing process to produce a camera-ready print book and e-book. This includes copyediting, designing layout templates, laying out the document in InDesign, and producing an index. My research is focused on the best practices and standards for publishing. Lessons learned from my research and experience include layout best practices, particularly linespacing and alignment guidelines, as well as the limitations and capabilities of InDesign, particularly its endnote functionality. Based on the results of this project, I can recommend self-publishers to understand the software and distribution platforms prior to publishing a book to ensure the required specifications are met to avoid complications later in the process. This document provides details on many of the software, distribution, and design options available for self-publishers to consider. Keywords: self-publishing, publishing, books, ebooks, book design, layout iii Dedication I dedicate this project to both of my grandmothers. I grew up watching you work hard, sacrifice, trust, and love with everything you have; it was beautiful; you are beautiful; and I hope I can model your example with a fraction of your grace and fruitfulness. Thank you for loving me so well.
  • A Study of Ancient Khmer Ephemerides

    A Study of Ancient Khmer Ephemerides

    A study of ancient Khmer ephemerides François Vernotte∗ and Satyanad Kichenassamy** November 5, 2018 Abstract – We study ancient Khmer ephemerides described in 1910 by the French engineer Faraut, in order to determine whether they rely on observations carried out in Cambodia. These ephemerides were found to be of Indian origin and have been adapted for another longitude, most likely in Burma. A method for estimating the date and place where the ephemerides were developed or adapted is described and applied. 1 Introduction Our colleague Prof. Olivier de Bernon, from the École Française d’Extrême Orient in Paris, pointed out to us the need to understand astronomical systems in Cambo- dia, as he surmised that astronomical and mathematical ideas from India may have developed there in unexpected ways.1 A proper discussion of this problem requires an interdisciplinary approach where history, philology and archeology must be sup- plemented, as we shall see, by an understanding of the evolution of Astronomy and Mathematics up to modern times. This line of thought meets other recent lines of research, on the conceptual evolution of Mathematics, and on the definition and measurement of time, the latter being the main motivation of Indian Astronomy. In 1910 [1], the French engineer Félix Gaspard Faraut (1846–1911) described with great care the method of computing ephemerides in Cambodia used by the horas, i.e., the Khmer astronomers/astrologers.2 The names for the astronomical luminaries as well as the astronomical quantities [1] clearly show the Indian origin ∗F. Vernotte is with UTINAM, Observatory THETA of Franche Comté-Bourgogne, University of Franche Comté/UBFC/CNRS, 41 bis avenue de l’observatoire - B.P.
  • New Traveling Exhibition from the Guild of Book Workers with 50 New Book Artists' Work Form Across the Country

    New Traveling Exhibition from the Guild of Book Workers with 50 New Book Artists' Work Form Across the Country

    New Traveling Exhibition from the Guild of Book Workers with 50 New Book Artists’ Work form Across the Country May 24, 2021 Contact Person: Jeanne Goodman Contact Email: [email protected] The Guild of Book Workers traveling exhibition will travel from June 2021 to September 2022. The opening and close dates for “Wild/LIFE” should be confirmed with each venue before travel and to check local public health precautions in place due to COVID-19. EXHIBITION “Wild/LIFE: Guild of Book Workers Triannual Exhibition”, June 2021 to September 2022 DESCRIPTION This exhibition features approximately 50 works by members of the Guild of Book Workers, an book artists organization that promotes interest in and awareness of the tradition of the book and paper arts by maintaining high standards of workmanship, hosting educational opportunities, and sponsoring exhibits. Members were invited to interpret the theme of “wildlife” in any way they wish, be it literal or abstract, humorous or serious. In a biological sense, wildlife describes the myriad of creatures sharing this planet, interacting and adapting, all connected to each other and their environment. "Wild" also describes an untamable essence that survives despite the constraints of society and culture. As craftspeople, knowledge of materials and keen observation of how they behave (and often how they refuse to comply) is an integral part of the practice of book making, and a reminder of how traditional bookbinding materials originate in nature. The exhibition opens at the American Bookbinders Museum in San Francisco, CA in June 2021, and will continue to travel to five additional venues across the country, closing in the fall of 2022.
  • Archaeology Book Collection 2013

    Archaeology Book Collection 2013

    Archaeology Book Collection 2013 The archaeology book collection is held on the upper floor of the Student Research Room (2M.25) and is arranged in alphabetical order. The journals in this collection are at the end of the document identified with the ‘author’ as ‘ZJ’. Use computer keys CTRL + F to search for a title/author. Abulafia, D. (2003). The Mediterranean in history. London, Thames & Hudson. Adkins, L. and R. Adkins (1989). Archaeological illustration. Cambridge, Cambridge University Press. Adkins, L. and R. A. Adkins (1982). A thesaurus of British archaeology. Newton Abbot, David & Charles. Adkins, R., et al. (2008). The handbook of British archaeology. London, Constable. Alcock, L. (1963). Celtic Archaeology and Art, University of Wales Press. Alcock, L. (1971). Arthur's Britain : history and archaeology, AD 367-634. London, Allen Lane. Alcock, L. (1973). Arthur's Britain: History and Archaeology AD 367-634. Harmondsworth, Penguin. Aldred, C. (1972). Akhenaten: Pharaoh of Egypt. London, Abacus; Sphere Books. Alimen, H. and A. H. Brodrick (1957). The prehistory of Africa. London, Hutchinson. Allan, J. P. (1984). Medieval and Post-Medieval Finds from Exeter 1971-1980. Exeter, Exeter City Council and the University of Exeter. Allen, D. F. (1980). The Coins of the Ancient Celts. Edinburgh, Edinburgh University Press. Allibone, T. E. and S. Royal (1970). The impact of the natural sciences on archaeology. A joint symposium of the Royal Society and the British Academy. Organized by a committee under the chairmanship of T. E. Allibone, F.R.S, London: published for the British Academy by Oxford University Press. Alves, F. and E.
  • Glossary Glossary

    Glossary Glossary

    Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts.
  • Syzygies a Conjunction Or an Opposition of the Sun with the Moon Occurs When the Elongation Between the Two Luminaries Is 0° Or

    Syzygies a Conjunction Or an Opposition of the Sun with the Moon Occurs When the Elongation Between the Two Luminaries Is 0° Or

    CHAPTER THIRTEEN SYZYGIES A conjunction or an opposition of the Sun with the Moon occurs when the elongation between the two luminaries is 0° or 180°, respec- tively. Syzygy is an astronomical term that refers both to conjunction and opposition. At mean syzygy, the double elongation, 2η ̄ = 0°, where ̄ ̄ ̄ ̄ η ̄ = λm – λs, and λm and λs are the mean longitudes of the Moon and the Sun. Analogously, at true syzygy, the double elongation, 2η = 0°, where η = λm – λs, and λm and λs are the true longitudes of the Moon and the Sun. The determination of the time from mean to true syzygy, ∆t, an essential step in the calculation of eclipses, was historically one of the major problems considered in computational astronomy (Chabás and Goldstein 1992 and 1997). Figure 20 represents a mean conjunction of the Sun and the Moon (indicated by the direction of S ̄ and M̄ ) and its corresponding true conjunction (indicated by the direction of S´ and M´). In this case, the ̄ ̄ mean conjunction (when λs = λm), which takes place at time t, comes M S̅ M̅ S S’ M’ λ’ = λ’s O m Aries 0° ̅̅ λλm = s Figure 20: Mean and true syzygies 140 chapter thirteen Table 13.1A: Some historical values of the mean synodic month Mean synodic month 29;31,50,7,37,27,8,25d Parisian Alfonsine Tables 29;31,50,7,54,25,3,32d Levi ben Gerson 29;31,50,8,9,20d al-Ḥajjāj’s Arabic trans. of the Almagest, Copernicus 29;31,50,8,9,24d Ibn Yūnus, al-Bitrūjị̄ 29;31,50,8,14,38d Ibn al-Kammād 29;31,50,8,19,50d al-Battānī 29;31,50,8,20d Almagest, Toledan Tables after the true conjunction λ( s´ = λm´), which occurs at time t´, so that ∆t = t´ – t < 0.
  • General Index

    General Index

    General Index Italicized page numbers indicate figures and tables. Color plates are in- cussed; full listings of authors’ works as cited in this volume may be dicated as “pl.” Color plates 1– 40 are in part 1 and plates 41–80 are found in the bibliographical index. in part 2. Authors are listed only when their ideas or works are dis- Aa, Pieter van der (1659–1733), 1338 of military cartography, 971 934 –39; Genoa, 864 –65; Low Coun- Aa River, pl.61, 1523 of nautical charts, 1069, 1424 tries, 1257 Aachen, 1241 printing’s impact on, 607–8 of Dutch hamlets, 1264 Abate, Agostino, 857–58, 864 –65 role of sources in, 66 –67 ecclesiastical subdivisions in, 1090, 1091 Abbeys. See also Cartularies; Monasteries of Russian maps, 1873 of forests, 50 maps: property, 50–51; water system, 43 standards of, 7 German maps in context of, 1224, 1225 plans: juridical uses of, pl.61, 1523–24, studies of, 505–8, 1258 n.53 map consciousness in, 636, 661–62 1525; Wildmore Fen (in psalter), 43– 44 of surveys, 505–8, 708, 1435–36 maps in: cadastral (See Cadastral maps); Abbreviations, 1897, 1899 of town models, 489 central Italy, 909–15; characteristics of, Abreu, Lisuarte de, 1019 Acequia Imperial de Aragón, 507 874 –75, 880 –82; coloring of, 1499, Abruzzi River, 547, 570 Acerra, 951 1588; East-Central Europe, 1806, 1808; Absolutism, 831, 833, 835–36 Ackerman, James S., 427 n.2 England, 50 –51, 1595, 1599, 1603, See also Sovereigns and monarchs Aconcio, Jacopo (d. 1566), 1611 1615, 1629, 1720; France, 1497–1500, Abstraction Acosta, José de (1539–1600), 1235 1501; humanism linked to, 909–10; in- in bird’s-eye views, 688 Acquaviva, Andrea Matteo (d.
  • Review (Abridged) of Bogle, Sophia S.W. Book Restoration Unveiled: an Essential Guide for Bibliophiles. [N.P.]: First Editions Press, 2019

    Review (Abridged) of Bogle, Sophia S.W. Book Restoration Unveiled: an Essential Guide for Bibliophiles. [N.P.]: First Editions Press, 2019

    Syracuse University From the SelectedWorks of Peter D Verheyen June, 2019 Review (Abridged) of Bogle, Sophia S.W. Book Restoration Unveiled: An Essential Guide for Bibliophiles. [n.p.]: First Editions Press, 2019. Peter D Verheyen This work is licensed under a Creative Commons CC_BY-NC-SA International License. Available at: https://works.bepress.com/peter_verheyen/54/ BOOK REVIEW by Peter D. Verheyen Book Restoration Unveiled - An Essential Guide for Bibliophiles <' ~ Sophia S. w Bogle I.... -::-,·::.. :-;:v->~~-.•;,-/..-ic·-<-.· -.. ,<:-/s-'.'7-.-·::-.)-_;.;~-':-"li-/}-~.\..... ~\-,,:~-;t-,\t-\'.?,.....,~~~j--.;t'.--;.;·-j~-}l: .....}-l-f.J ~ u 0 (Ashland, OR: First Editions Press, 2019) :::0 (D o' 5: In Book Restoration Unveiled, Sophia S.W Bogle Book Restoration (D r6 sets out "to provide the tools to spot restorations so ~ that everyone can make more informed decisions s'-I when buying or selling books." The second reason was CJ UnvedJ c% p.J her realization that "instead of a simple list of clear "D 8 0 0 terminology, [there] was a distressing lack of agreement ~ ~ (") (D and even confusion about the most basic of book repair 0 () 8 ~ If ......__ (D terms." She writes, "this book [is] a bridge between the Iv :::0 /,8'~.4' 0 ....... world of collecting, buying, and selling books, and that <..O-< (D ......__ '-I of book repair, restoration, and conservation." In the ~ 0 (D case of the latter, she describes some of the minutiae ::: ~- 8" ~ 0 (") of the book such as structure, and treatments, good ;;,;- p.J ~ :::0 as well as bad. But, "this is not a 'how-to' manual." (D u ~ (D Rather, it is a "guide to help you understand the world S; o' of restoration, to recognize restorations, and to choose §.
  • Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography on the Occasion of the 50Th Anniversary of Apollo 11 Moon Landing

    Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography on the Occasion of the 50Th Anniversary of Apollo 11 Moon Landing

    Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography On the occasion of the 50th anniversary of Apollo 11 moon landing Please note: A specific item in this catalogue may be sold or is on hold if the provided link to our online inventory (by clicking on the blue-highlighted author name) doesn't work! Milestones of Science Books phone +49 (0) 177 – 2 41 0006 www.milestone-books.de [email protected] Member of ILAB and VDA Catalogue 07-2019 Copyright © 2019 Milestones of Science Books. All rights reserved Page 2 of 71 Authors in Chronological Order Author Year No. Author Year No. BIRT, William 1869 7 SCHEINER, Christoph 1614 72 PROCTOR, Richard 1873 66 WILKINS, John 1640 87 NASMYTH, James 1874 58, 59, 60, 61 SCHYRLEUS DE RHEITA, Anton 1645 77 NEISON, Edmund 1876 62, 63 HEVELIUS, Johannes 1647 29 LOHRMANN, Wilhelm 1878 42, 43, 44 RICCIOLI, Giambattista 1651 67 SCHMIDT, Johann 1878 75 GALILEI, Galileo 1653 22 WEINEK, Ladislaus 1885 84 KIRCHER, Athanasius 1660 31 PRINZ, Wilhelm 1894 65 CHERUBIN D'ORLEANS, Capuchin 1671 8 ELGER, Thomas Gwyn 1895 15 EIMMART, Georg Christoph 1696 14 FAUTH, Philipp 1895 17 KEILL, John 1718 30 KRIEGER, Johann 1898 33 BIANCHINI, Francesco 1728 6 LOEWY, Maurice 1899 39, 40 DOPPELMAYR, Johann Gabriel 1730 11 FRANZ, Julius Heinrich 1901 21 MAUPERTUIS, Pierre Louis 1741 50 PICKERING, William 1904 64 WOLFF, Christian von 1747 88 FAUTH, Philipp 1907 18 CLAIRAUT, Alexis-Claude 1765 9 GOODACRE, Walter 1910 23 MAYER, Johann Tobias 1770 51 KRIEGER, Johann 1912 34 SAVOY, Gaspare 1770 71 LE MORVAN, Charles 1914 37 EULER, Leonhard 1772 16 WEGENER, Alfred 1921 83 MAYER, Johann Tobias 1775 52 GOODACRE, Walter 1931 24 SCHRÖTER, Johann Hieronymus 1791 76 FAUTH, Philipp 1932 19 GRUITHUISEN, Franz von Paula 1825 25 WILKINS, Hugh Percy 1937 86 LOHRMANN, Wilhelm Gotthelf 1824 41 USSR ACADEMY 1959 1 BEER, Wilhelm 1834 4 ARTHUR, David 1960 3 BEER, Wilhelm 1837 5 HACKMAN, Robert 1960 27 MÄDLER, Johann Heinrich 1837 49 KUIPER Gerard P.
  • COURT of CLAIMS of THE

    COURT of CLAIMS of THE

    REPORTS OF Cases Argued and Determined IN THE COURT of CLAIMS OF THE STATE OF ILLINOIS VOLUME 39 Containing cases in which opinions were filed and orders of dismissal entered, without opinion for: Fiscal Year 1987 - July 1, 1986-June 30, 1987 SPRINGFIELD, ILLINOIS 1988 (Printed by authority of the State of Illinois) (65655--300-7/88) PREFACE The opinions of the Court of Claims reported herein are published by authority of the provisions of Section 18 of the Court of Claims Act, Ill. Rev. Stat. 1987, ch. 37, par. 439.1 et seq. The Court of Claims has exclusive jurisdiction to hear and determine the following matters: (a) all claims against the State of Illinois founded upon any law of the State, or upon an regulation thereunder by an executive or administrative ofgcer or agency, other than claims arising under the Workers’ Compensation Act or the Workers’ Occupational Diseases Act, or claims for certain expenses in civil litigation, (b) all claims against the State founded upon any contract entered into with the State, (c) all claims against the State for time unjustly served in prisons of this State where the persons imprisoned shall receive a pardon from the Governor stating that such pardon is issued on the grounds of innocence of the crime for which they were imprisoned, (d) all claims against the State in cases sounding in tort, (e) all claims for recoupment made by the State against any Claimant, (f) certain claims to compel replacement of a lost or destroyed State warrant, (g) certain claims based on torts by escaped inmates of State institutions, (h) certain representation and indemnification cases, (i) all claims pursuant to the Law Enforcement Officers, Civil Defense Workers, Civil Air Patrol Members, Paramedics and Firemen Compensation Act, (j) all claims pursuant to the Illinois National Guardsman’s and Naval Militiaman’s Compensation Act, and (k) all claims pursuant to the Crime Victims Compensation Act.
  • The Project Gutenberg Ebook #31428: Matter, Ether, and Motion

    The Project Gutenberg Ebook #31428: Matter, Ether, and Motion

    The Project Gutenberg EBook of Matter, Ether, and Motion, Rev. ed., enl., by Amos Emerson Dolbear This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Matter, Ether, and Motion, Rev. ed., enl. The Factors and Relations of Physical Science Author: Amos Emerson Dolbear Release Date: February 27, 2010 [EBook #31428] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK MATTER, ETHER, AND MOTION *** Produced by Andrew D. Hwang, Peter Vachuska, Chuck Greif and the Online Distributed Proofreading Team at http://www.pgdp.net transcriber’s note Minor typographical corrections and presentational changes have been made without comment. Illustrations may have been moved slightly relative to the surrounding text. Aside from clear misspellings, every effort has been made to preserve variations of spelling and hyphenation from the original. This PDF file is optimized for screen viewing, but may easily be recompiled for printing. Please see the preamble of the LATEX source file for instructions. By Profe&or A. E. Dol´ar MATTER, ETHER AND MOTION The Factors and Relations of Physical Science Enlarged Edition Cloth Illustrated $2.00 THE TELEPHONE With directions for making a Speaking Telephone Illustrated 50 cents THE ART OF PROJECTING A Manual of Experimentation in Physics, Chemistry, and Natural History, with the Porte Lumiere` and Magic Lantern New Edition Revised Illustrated $2.00 Lee and S˙«rd Publis˙rs Bo<on Matter,Ether, and Motion THE FACTORS AND RELATIONS OF PHYSICAL SCIENCE BY A.