Exploring Best Practices in Developmental Mathematics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Teaching-Math-Middle-School-Excerpt
FOR MORE, go to https://products.brookespublishing.com/Teaching-Math-in-Middle-School-P1132.aspx Teaching Math in Middle School Using MTSS to Meet All Students’ Needs Excerpted from Teaching Math in Middle School, By Leanne R. Ketterlin-Geller Ph.D., Sarah R. Powell Ph.D., David J. Chard Ph.D., Lindsey Perry Ph.D. Ketterlin-Geller-FM_Final.indd 1 5/20/19 11:39 PM FOR MORE, go to https://products.brookespublishing.com/Teaching-Math-in-Middle-School-P1132.aspx Teaching Math in Middle School Using MTSS to Meet All Students’ Needs by Leanne R. Ketterlin-Geller, Ph.D. Southern Methodist University Dallas, Texas Sarah R. Powell, Ph.D. The University of Texas at Austin David J. Chard, Ph.D. Boston University Massachusetts and Lindsey Perry, Ph.D. Southern Methodist University Dallas, Texas Baltimore • London • Sydney Excerpted from Teaching Math in Middle School, By Leanne R. Ketterlin-Geller Ph.D., Sarah R. Powell Ph.D., David J. Chard Ph.D., Lindsey Perry Ph.D. Ketterlin-Geller-FM_Final.indd 3 5/20/19 11:39 PM FOR MORE, go to https://products.brookespublishing.com/Teaching-Math-in-Middle-School-P1132.aspx Paul H. Brookes Publishing Co. Post Office Box 10624 Baltimore, Maryland 21285-0624 USA www.brookespublishing.com Copyright © 2019 by Paul H. Brookes Publishing Co., Inc. All rights reserved. “Paul H. Brookes Publishing Co.” is a registered trademark of Paul H. Brookes Publishing Co., Inc. Typeset by Absolute Services Inc., Towson, Maryland. Manufactured in the United States of America by Sheridan Books, Chelsea, Michigan. Unless otherwise stated, examples in this book are composites. -

Exponents and Polynomials
For use by Palm Beach State College only. CHAPTER 5 Exponents and Polynomials 5.1 Exponents 5.2 Adding and Subtracting Polynomials 5.3 Multiplying Polynomials 5.4 Special Products Integrated Review—Exponents and Operations on Polynomials 5.5 Negative Exponents and Scientific Notation 5.6 Dividing Polynomials CHECK YOUR PROGRESS Vocabulary Check Chapter Highlights Chapter Review Getting Ready for the Test Can You Imagine a World Without the Internet? Chapter Test In 1995, less than 1% of the world population was connected to the Internet. By 2015, Cumulative Review that number had increased to 40%. Technology changes so fast that, if this trend continues, by the time you read this, far more than 40% of the world population will be connected to the Internet. The circle graph below shows Internet users by region of Recall from Chapter 1 that an exponent is a the world in 2015. In Section 5.2, Exercises 103 and 104, we explore more about the shorthand notation for repeated factors. This growth of Internet users. chapter explores additional concepts about exponents and exponential expressions. An especially useful type of exponential expression is a polynomial. Polynomials model many real- world phenomena. In this chapter, we focus on polynomials and operations on polynomials. Worldwide Internet Users 3500 Worldwide Internet Users 3000 (by region of the world) (in milions) 2500 Oceania Europe 2000 Asia 1500 Africa 1000 500 Number of Internet Users Americas 0 1995 2000 2005 2010 2015 Year Data from International Telecommunication Union and United Nations Population Division 310 Copyright Pearson. All rights reserved. M05_MART8978_07_AIE_C05.indd 310 11/9/15 5:45 PM For use by Palm Beach State College only. -

Elementary Algebra
ELEMENTARY ALGEBRA Overview The Elementary Algebra section of ACCUPLACER contains 12 multiple choice Algebra questions that are similar to material seen in a Pre-Algebra or Algebra I pre-college course. A calculator is provided by the computer on questions where its use would be beneficial. On other questions, solving the problem using scratch paper may be necessary. Expect to see the following concepts covered on this portion of the test: Operations with integers and rational numbers, computation with integers and negative rationals, absolute values, and ordering. Operations with algebraic expressions that must be solved using simple formulas and expressions, adding and subtracting monomials and polynomials, multiplying and dividing monomials and polynomials, positive rational roots and exponents, simplifying algebraic fractions, and factoring. Operations that require solving equations, inequalities, and word problems, solving linear equations and inequalities, using factoring to solve quadratic equations, solving word problems and written phrases using algebraic concepts, and geometric reasoning and graphing. Testing Tips Use resources provided such as scratch paper or the calculator to solve the problem. DO NOT attempt to only solve problems in your head. Start the solving process by writing down the formula or mathematic rule associated with solving the particular problem. Put your answer back into the original problem to confirm that your answer is correct. Make an educated guess if you are unsure of the answer. Algebra Tips Test -

Algebra 1 Skills Needed to Be Successful in Algebra 2
Algebra 1 Skills Needed to be Successful in Algebra 2 A. Simplifying Polynomial Expressions Objectives: The student will be able to: • Apply the appropriate arithmetic operations and algebraic properties needed to simplify an algebraic expression. • Simplify polynomial expressions using addition and subtraction. • Multiply a monomial and polynomial. B. Solving Equations Objectives: The student will be able to: • Solve multi-step equations. • Solve a literal equation for a specific variable, and use formulas to solve problems. C. Rules of Exponents Objectives: The student will be able to: • Simplify expressions using the laws of exponents. • Evaluate powers that have zero or negative exponents. D. Binomial Multiplication Objectives: The student will be able to: • Multiply two binomials. E. Factoring Objectives: The student will be able to: • Identify the greatest common factor of the terms of a polynomial expression. • Express a polynomial as a product of a monomial and a polynomial. • Find all factors of the quadratic expression ax2 + bx + c by factoring and graphing. F. Radicals Objectives: The student will be able to: • Simplify radical expressions. G. Graphing Lines Objectives: The student will be able to: • Identify and calculate the slope of a line. • Graph linear equations using a variety of methods. • Determine the equation of a line. H. Regression and Use of the Graphing Calculator Objectives: The student will be able to: • Draw a scatter plot, find the line of best fit, and use it to make predictions. • Graph and interpret real-world situations using linear models. 4 A. Simplifying Polynomial Expressions I. Combining Like Terms - You can add or subtract terms that are considered "like", or terms that have the same variable(s) with the same exponent(s). -

Order of Operations, Plus Tidbits on Handling Equations Notes by Eric Hoyle –
Order of Operations, plus tidbits on handling equations Notes by Eric Hoyle – www.hoyletutoring.com Parentheses Exponents Multiplication Division Addition Subtraction Most math students are familiar with this order of operations and some way to remember it. This is good enough for basic math, but not for algebra. These notes should explain the nuances of order of operations that are important for mainstream algebra. 1. Symbols for multiplication a) The “ x ” symbol. This should be avoided after basic math, because it looks like the variable “x”. b) The “ · ” symbol. The dot should be written high enough that it does not look like a decimal point. c) Juxtaposition (putting beside). This is the usual way to write multiplication when variables are involved. Examples: 2x = 2 · x ; 4abc = 4 · a · b · c 2. Symbols for division a) The “ ÷ ” symbol. This is rarely used after basic math. b) The “ / ” symbol. The slash means the same as the ÷ symbol, and is commonly used on calculators and computers. c) The fraction bar. This is usually the preferred way to write division, because the fraction bar is a grouping symbol that is easier to read than parentheses. More on this below. 3. Addition and subtraction have the same priority. Subtraction is adding a negative number, so it is equal to addition for purposes of order of operations. One way to give the same level of priority to addition and subtraction is to work both operations as they occur from left to right. For example: Incorrect Method (add then subtract) Correct Method (both, left to right) 2 + 3 – 4 + 8 – 5 2 + 3 – 4 + 8 – 5 5 – 4 + 8 – 5 5 – 4 + 8 – 5 5 – 12 – 5 1 + 8 – 5 -7 – 5 9 – 5 -12 4 Doing all the addition first causes the 4 and 8 to group together, and subtracts them both. -

Copyrighted Material
26_169841 bindex.qxd 2/29/08 2:58 PM Page 365 Index addition law, for limits, 345 Symbols and Numerics additive identity, 14 > (greater than), 21 additive inverse property, 14 ≥ (greater than or equal to), 21 advanced identities, described, 195 < (less than) symbol, 21 Algebra, Fundamental Theorem of, 82–83, 95 ≤ (less than or equal to), 21 algebra, labeling and expressing ellipses, θ (theta) 269–270 graphing calculator, entering as a variable algebra I and II, compared to pre-calculus, 10 in, 251–252 Algebra I and II Workbook For Dummies as the input of a trig function, 147 (Sterling), 240, 356 length of radius, 243 Algebra II For Dummies (Sterling), 240 as plotting point, 244 algebraic expressions, simplifying, 178 theta prime, as the name given to the algebraic method, to find limit, 342–345 reference angle, 141 amplitude in trig functions, 125 changing, 160–163, 168–169 2 x 2 matrix, inverse of, 310 defined, 160 2(π) radian, 150 period, compared to, 165 3 x 3 system of equations, and Cramer’s positive values of, 161 rule, 314 sine functions, 161–163 30-60 triangle, 132–133, 135 transformations, combining, 167–170 45er triangle, 131–132, 138 analytical method for finding a limit, 360, convenience of, 120 341–342 AND statement, 25 angle(s) • A • arc as, 145 central, 145–146 AAS (Angle Angle Side) triangle, solving, common, 128–129 218, 220–221 correct placement, 134–136 absolute value, 13, 22–24, 36, 48 cosine of, 122–123 absolute-value functions, 36 in degrees, 197 acceleration, moving objects with, 338 doubling the trig value of, 205–207 -

Interlibrar Loan
The WSU Libraries' goal is to provide excellent customer service. Let us know how we are doing by responding to this short survey: https://libraries.wsu.edu/access_services_survey International Journal of Mathematical Education in Science and Technology ISSN: 0020-739X (Print) 1464-5211 (Online) Journal homepage: https://www.tandfonline.com/loi/tmes20 Consequences of FOIL for undergraduates Lori Koban & Simone Sisneros-Thiry To cite this article: Lori Koban & Simone Sisneros-Thiry (2015) Consequences of FOIL for undergraduates, International Journal of Mathematical Education in Science and Technology, 46:2, 205-222, DOI: 10.1080/0020739X.2014.950706 To link to this article: https://doi.org/10.1080/0020739X.2014.950706 Published online: 22 Sep 2014. Submit your article to this journal Article views: 128 View related articles View Crossmark data Citing articles: 2 View citing articles Full Terms & Conditions of access and use can be found at https://www.tandfonline.com/action/journalInformation?journalCode=tmes20 International Journal of Mathematical Education in Science and Technology, 2015 Vol. 46, No. 2, 205–222, http://dx.doi.org/10.1080/0020739X.2014.950706 Consequences of FOIL for undergraduates Lori Koban∗ and Simone Sisneros-Thiry Department of Mathematics and Computer Science, University of Maine at Farmington, Farmington, ME, USA (Received 6 May 2014) FOIL is a well-known mnemonic that is used to find the product of two binomials. We conduct a large sample (n = 252) observational study of first-year college students and show that while the FOIL procedure leads to the accurate expansion of the product of two binomials for most students who apply it, only half of these students exhibit conceptual understanding of the procedure. -

Algebra 1 Skills Needed to Be Successful in Algebra 2
amt Algebra 1 Skills Needed to be Successful in Algebra 2 A. Simplifying Polynomial Expressions Objectives: The student will be able to: Apply the appropriate arithmetic operations and algebraic properties needed to simplify an algebraic expression. Simplify polynomial expressions using addition and subtraction. Multiply a monomial and polynomial. B. Solving Equations Objectives: The student will be able to: Solve multi-step equations. Solve a literal equation for a specific variable, and use formulas to solve problems. C. Rules of Exponents Objectives: The student will be able to: Simplify expressions using the laws of exponents. Evaluate powers that have zero or negative exponents. D. Binomial Multiplication Objectives: The student will be able to: Multiply two binomials. E. Factoring Objectives: The student will be able to: Identify the greatest common factor of the terms of a polynomial expression. Express a polynomial as a product of a monomial and a polynomial. Find all factors of the quadratic expression ax + bx + c by factoring and graphing. F. Radicals Objectives: The student will be able to: Simplify radical expressions. G. Graphing Lines Objectives: The student will be able to: Identify and calculate the slope of a line. Graph linear equations using a variety of methods. Determine the equation of a line. H. Regression and Use of the Graphing Calculator Objectives: The student will be able to: Draw a scatter plot, find the line of best fit, and use it to make predictions. Graph and interpret real-world situations using linear models. A. Simplifying Polynomial Expressions I. Combining Like Terms You can add or subtract terms that are considered "like", or terms that have the same variable(s) with the same exponent(s). -

Succeeding at Math!
Succeeding at Math! By: Lesley Baker How You Learn Three ways of learning are by conditioning, thinking and a combination of conditioning and thinking. Conditioning – learning things with a maximum of physical and emotional reaction and a minimum of thinking. ◦ Example: Repeating the word “pi” to yourself and practicing where the symbol is found on the calculator are two forms of conditioned learning. You are are learning, using your voice and your eye-hand coordination (physical activities), and you are doing very little thinking. (Nolting, 2002) How You Learn Thinking – Defined as learning with a maximum of thought and a minimum of emotional and physical reaction. ◦ Example: Learning about “pi” by thinking is different than learning about it by conditioning. To learn “pi” by thinking, you would have to do the calculations necessary to result in the numeric value which the word “pi” represents. You are learning, use your mind (thought activities), and you are using very little emotional or physical energy to learn “pi” in this way. (Nolting, 2002) How You Learn The most successful way to combine thinking and conditioning is to learn by thinking first and conditioning second. Learning by thinking means that you learn by ◦ Observing ◦ Processing, and ◦ Understanding the information. (Nolting, 2002) Using Your Best Learning Sense/Style to Improve Memory Using your learning sense or learning style and decreasing distraction while studying are very efficient ways to learn. Using your best learning sense can improve how well you learn and enhance the transfer of knowledge into long-term memory/reasoning. ◦ Your learning senses are vision, hearing, touching, etc. -
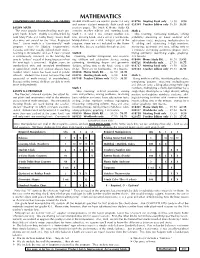
MATHEMATICS COMPREHENSIVE PROGRAMS - ALL GRADES Student Workbooks Are Used in Grades 1-3 Only 018726 Meeting Book Only 13.50 8 50
MATHEMATICS COMPREHENSIVE PROGRAMS - ALL GRADES Student Workbooks are used in grades 1-3 only 018726 Meeting Book only 13.50 8 .50 and contain student materials, flash cards and 021349 Teacher Edition only 59.50 36 .95 SAXON MATH practice pages. The Math K Home Study Kit The most popular homeschooling math pro- contains teacher edition and meeting book. Math 2 gram hands down! Highly recommended by Math 1, 2, and 3 kits contain teacher edi- Skip counting; comparing numbers; solving both Mary Pride and Cathy Duffy, Saxon Math tion, meeting book, and a set of 2 workbooks. problems; mastering all basic addition and also wins our award for the “Most Requested Manipulatives are a vital, integral part of the subtraction facts; mastering multiplication to Text.” Saxon math is a “user-friendly” math program; these are not included in the Home 5; adding and subtracting 2-digit numbers; program - even for Algebra, Trigonometry, Study Kits, but are available through us also. measuring; perimeter and area; telling time to Calculus and other usually difficult math topics. 5 minutes; identifying geometric shapes; iden- Learning is incremental and each new concept Math K tifying symmetry; identifying angles; graphing. is continuously reviewed, so the learning has Counting, number recognition, and sequenc- 132 lessons. time to “sink in” instead of being forgotten when ing; addition and subtraction stories; sorting; 018400 Home Study Kit . 96.50 59 .95 the next topic is presented. Higher scores on patterning, identifying shapes and geometric 001526 Workbooks only . 27.50 16 .75 standardized tests and increased enrollments designs; telling time to the hour; using a cal- 018727 Meeting Book only 13.50 8 .50 in upper-level math and science classes have endar. -

Math Handbook of Formulas, Processes and Tricks Algebra And
Math Handbook of Formulas, Processes and Tricks (www.mathguy.us) Algebra and PreCalculus Prepared by: Earl L. Whitney, FSA, MAAA Version 2.8 April 19, 2016 Copyright 2008‐16, Earl Whitney, Reno NV. All Rights Reserved Algebra Handbook Table of Contents Page Description Chapter 1: Basics 9Order of Operations (PEMDAS, Parenthetical Device) 10 Graphing with Coordinates (Coordinates, Plotting Points) 11 Linear Patterns (Recognition, Converting to an Equation) 12 Identifying Number Patterns 13 Completing Number Patterns 14 Basic Number Sets (Sets of Numbers, Basic Number Set Tree) Chapter 2: Operations 15 Operating with Real Numbers (Absolute Value, Add, Subtract, Multiply, Divide) 16 Properties of Algebra (Addition & Multiplication, Zero, Equality) Chapter 3: Solving Equations 18 Solving Multi‐Step Equations 19 Tips and Tricks in Solving Multi‐Step Equations Chapter 4: Probability & Statistics 20 Probability and Odds 21 Probability with Dice 22 Combinations 23 Statistical Measures Chapter 5: Functions 24 Introduction to Functions (Definitions, Line Tests) 25 Special Integer Functions 26 Operations with Functions 27 Composition of Functions 28 Inverses of Functions 29 Transformation – Translation 30 Transformation – Vertical Stretch and Compression 31 Transformation – Horizontal Stretch and Compression 32 Transformation – Reflection 33 Transformation – Summary 34 Building a Graph with Transformations Version 2.8 Page 2 of 178 April 19, 2016 Algebra Handbook Table of Contents Page Description Chapter 6: Linear Functions 35 Slope of a Line (Mathematical -

Math 100B Textbook
Beginning Algebra MATH 100B Math Study Center BYU-Idaho Preface This math book has been created by the BYU-Idaho Math Study Center for the college student who needs an introduction to Algebra. This book is the product of many years of implementation of an extremely successful Beginning Algebra program and includes perspectives and tips from experienced instructors and tutors. Videos of instruction and solutions can be found at the following url: https://youtu.be/-taqTmqALPg?list=PL_YZ8kB-SJ1v2M-oBKzQWMtKP8UprXu8q The following individuals have assisted in authoring: Rich Llewellyn Daniel Baird Diana Wilson Kelly Wilson Kenna Campbell Robert Christenson Brandon Dunn Hannah Sherman We hope that it will be helpful to you as you take Algebra this semester. The BYU-Idaho Math Study Center Math 100B Table of Contents Chapter 1 – Arithmetic and Variables Section 1.1 – LCM and Factoring…..……………………………………………………………6 Finding factors, Prime Factorization, Least Common Multiples Section 1.2 – Fractions…………………………………………………………………………..14 Addition, Subtraction, Multiplication, Division Section 1.3 – Decimals, Percents………………………………………………………..……….21 Decimals; Conversion between decimals, fractions, and percents; finding percents of totals Section 1.4 – Rounding, Estimation, Exponents, Roots, and Order of Operations…...…………28 Natural number exponents and roots of integers Section 1.5 – Variables and Geometry ……………………………………………………….…39 Introductions to variables and their use in formulas Section 1.6 – Negative and Signed Numbers...…………………………………………………..51 Section