DOCSLIB.ORG

Hausdorff Dimension of Quasi-Circles

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hausdorff Dimension of Quasi-Circles PUBLICATIONS MATHÉMATIQUES DE L’I.H.É.S. RUFUS BOWEN Hausdorff dimension of quasi-circles Publications mathématiques de l’I.H.É.S., tome 50 (1979), p. 11-25 <http://www.numdam.org/item?id=PMIHES_1979__50__11_0> © Publications mathématiques de l’I.H.É.S., 1979, tous droits réservés. L’accès aux archives de la revue « Publications mathématiques de l’I.H.É.S. » (http:// www.ihes.fr/IHES/Publications/Publications.html) implique l’accord avec les conditions géné- rales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou im- pression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ HAUSDORFF DIMENSION OF QUASI-CIRCLES by RUFUS BOWEN (1) Let G be the group of all linear fractional transformations taking the unit disk U onto itself. One calls a discrete subgroup F C G a surface group if U/F is a compact surface without braitch points. This paper concerns the relation between two such groups I\ and I\ yielding the same topological surface. This is a classical and well- developed problem [6]; what is novel here is the application of the Gibbs measures of statistical mechanics and dynamical systems. The groups r\ and Fg as above are isomorphic since each is isomorphic to the fundamental group of the surface. Furthermore, for any isomorphism a : Fi—^Fg there is an interesting homeomorphism h•.Sl—^Sl of the circle S1^^^:]^^!} so that: A(40=a(^)A(0 for ^eFi, ^eS1.' This homeomorphism A, which is unique, is called the boundary correspondence (Fenchel and Nielsen, see [n], [14], or [22]). Let G* be the group of linear fractional trans- formations taking S1 onto itself. (G has index 2 in G*). We will give a new proof of the following result of Mostow [13]: Theorem 2. — The boundary homeomorphism h is a linear fractional transformation if it is absolutely continuous. Now recall the quasi-Fuchsian group A==A(Fi, Fg, a) [6] associated to the pair of Fuchsian groups F^, Fg, and a given abstract isomorphism a: Fi—^Fg. This is a discrete group A of linear fractional transformations of the extended complex plane (C == S2) which simultaneously uniformizes the surfaces U/F^ in the following sense: (i) There is a Jordan curve y m S2 (called a quasi-circle) with ^M^T ^or a^ elements ^ in A, and each orbit of A is dense in y* (*) Partially supported by NSF MCS74-19388^01. 259 12 RUFUS BOWEN (ii) There are analytic diffeomorphisms ^: U->D^ where D^, Dg are connected components of S^y so that a,(^)=^-lo^Fo^ belongs to F, for all ^eA and a,: A-^F, is an isomorphism, and (iii) agoa^1 is the given isomorphism a : r^-^rg. The curve y is generally not smooth nor even rectifiable [5, p. 263]. Y is a round circle (Theorem i) Y is a genuine quasi-circle (Theorem 2) FIG. i Theorem 2. — Suppose I\ and I\ are not conjugate as Fuchsian groups^ namely via (BeG*. Then the Hausdorff dimension a of y is greater than i. Furthermore O<^(Y)<OO, where v^ is a-dimensional Hausdorff measure^ and ^ | y is ergodic under A. The paper starts with a variant of the Nielsen development. This associates symbol sequences (generalized c< decimal expansion 33) to points in SMn a way determined by r^. The reader familiar with dynamical systems will recognize this as a cc Markov partition for 1^ 55. Via this construction functions and measures are transferred from the circle (where they have geometric meaning) to the Cantor set of symbol sequences (where they can be analyzed). The paper ends with results on Schottky groups, where the symbolic sequences are quite transparent. The author thanks Dennis Sullivan for introducing him to Kleinian groups and Hedlund for his paper [9] which motivated the present one. i. Nielsen Development. Let FOG* be a surface group. A piecewise smooth map f:Sl->Sl is called Markov for F if one can partition S1 into segments Ii, ..., 1^ so that: (i) f\^k=fk\^ some /^er, and (ii) for each k, f(l^) is the union of various Ij's. 260 HAUSDORFF DIMENSION OF QUASI-GIRCLES 13 Condition (ii) can be rephrased as follows. Letting W be the set of endpoints of the I^'s, consider each such point to be really two points, depending on which 1^; it is associated with. Then condition (ii) is equivalent to ./(W) C W. The idea of a Markov map is to replace the action of the group F on S1 by the single map f. For each g^2 let O^ be a surface group of genus g whose fundamental domain R in U is a regular 4^-sided noneuclidean polygon ([9], [12], [18, p. 89]). The Nielsen development is a certain Markov map for O^ ([9], [14, pp. 211-217]). We shall construct variants which are more suitable for our purposes. Each angle ofRis a= — and each vertex of R belongs to 4^ distinct translates <p(R), (pe0^. The net 91 is defined to be the collection of all sides and vertices of all translates <p(R), (pe^. This net has the following crucial property: (*) the entire noneuclidean geodesic passing through any edge in 91 is contained in 91. Let V be the set of vertices in 91 which are adjacent in 91 to vertices of R but are not themselves vertices ofR. The set Vis contained in the set of vertices of the noneucli- dean polygon R which is the union of R plus all the translates <p(R) which touch R. The polygon R is convex since each interior angle equals 2a<7i;. For each vertex^ of 91 let W be the set of 4^ points on S1 which are the points at infinity of the 2g noneuclidean geodesies in 91 passing through p. Letting W== U Wy, property (*) implies that: WgCW for q a vertex of R. Recall now a set of generators for 0^ (fo]? E1^], [18]). Divide the sides of R into g groups of 4 consecutive sides; label thej-th group ^, ^, a^~1, b^1. Gall a^ and a^1 (and b^ and b^1) corresponding sides. For each side s of R there is an element ^se(^g so that: (p^)=:Rn(pg(R)==side corresponding to s. The set {93} generates 0.. Let Jg be the smaller segment of S1 whose endpoints are the points at infinity of the noneuclidean geodesic through s. Lemma L — <p,CLnW)CW. Proof. — The geodesies passing through nonconsecutive sides of R do not intersect. One way of checking this well-known fact is by an area argument. If two such geodesies intersected (perhaps at oo), then, they together with m sides (m^-1) of R would form a polygon containing R and with noneuclidean area less than mn^^g—3)^. This polygon contains at least 2g translates of R, each having area (4^—4.)n. So 2s{4•g—4)^4«?—'33 which is impossible since g^-2. We claim that J^nWC U W where Tg is the set of vertices in 91 adjacent to p(=Ts * an endpoint ofs. Now (p^(T^)CVu{ vertices ofR} because 9^) is a side ofR. Hence the above claim would yield: 9,(J,nW)CTs\Js ; ^^U W.CW.p 261 14 RUFUS BO WEN Suppose ^eJ,nW but u^ U, Wp. Let y be a geodesic in SR from some ^eV\T, to u. Let ^, ^ be the vertices of R on the geodesic a through s; let r^, ^ be the vertices of R adjacent to ^, ^ respectively and exterior to the domain bounded by a and Jg. Let (B, be the geodesic containing a side of R, passing through r, but not q^ Then (B, and a do not intersect as they pass through nonconsecutive sides of an image 9(R). Since the endpoints of J, are in W^uW^, and fteT,, one has ueintj,. Therefore the geodesic y must cut the geodesic a; this intersection ^is a vertex of the net. If q lay between q^ and q^, then ^ would be an endpoint of s and ue U W . Suppose 'q lies between q^ and S1 on a. PE s Consider the region Q in the unit disk exterior to the half disks bounded by the geodesies a, (B^ and Pa. Because (B^, [Bg are sides of the convex polygon K, the point qeR above lies in Q. Because Qis convex the geodesic ^ C y from y to ^lies in Q^. ^ must now intersect r^; this intersection is a vertex of the next, hence r^ or q^ Either case gives a contradiction. • Let v be a vertex of R, belonging to the sides s and ^' of R. We will construct a segment J(y)Cint(J,nJ,,). Let j^'eV be the vertices of the net 91 adjacent to v in yi and lying on the geodesies a and a' through j and s\ Choose vertices q, q' of R so that ^, v,p\ q' are consecutive vertices of a translate <p(R), ^eO.- The geodesies (B, p' containing j&y, j^' do not intersect; they intersect S1 at points w{v}, ^(^eint^nj^). LetJ(y) be the interval [w{v), ^'(^)]CS1. The endpoints w{v), w\v) of]{v) are in,W; arguments analogous to the proof of Lemma i show that WnintJ(y)==0. Theorem 0. — A surface group FCG has transitive Markov maps on S1.
Load more

Recommended publications
  • Möbius Transformations
    Möbius transformations Möbius transformations are simply the degree one rational maps of C: az + b σ : z 7! : ! A cz + d C C where ad − bc 6= 0 and a b A = c d Then A 7! σA : GL(2C) ! fMobius transformations g is a homomorphism whose kernel is ∗ fλI : λ 2 C g: The homomorphism is an isomorphism restricted to SL(2; C), the subgroup of matri- ces of determinant 1. We have an action of GL(2; C) on C by A:(B:z) = (AB):z; A; B 2 GL(2; C); z 2 C: The action of SL(2; R) preserves the upper half-plane fz 2 C : Im(z) > 0g and also R [ f1g and the lower half-plane. The action of the subgroup a b SU(1; 1) = : jaj2 − jbj2 = 1 b a preserves the open unit disc, the closed unit disc, and its exterior. All of these actions are transitive that is, for all z and w in the domain there is A in the group with A:z = w. Kleinian groups Definition 1 A Kleinian group is a subgroup Γ of P SL(2; C) which is discrete, that is, there is an open neighbourhood U ⊂ P SL(2; C) of the identity element I such that U \ Γ = fIg: Definition 2 A Fuchsian group is a discrete subgroup of P SL(2; R) Equivalently (as usual with topological groups) there is an open neighbourhood V of I such that γV \ γ0V = ; for all γ, γ0 2 Γ, γ 6= γ0. To get this, choose V with V = V −1 and V:V ⊂ U.
    [Show full text]
  • Handlebody Orbifolds and Schottky Uniformizations of Hyperbolic 2-Orbifolds
    proceedings of the american mathematical society Volume 123, Number 12, December 1995 HANDLEBODY ORBIFOLDS AND SCHOTTKY UNIFORMIZATIONS OF HYPERBOLIC 2-ORBIFOLDS MARCO RENI AND BRUNO ZIMMERMANN (Communicated by Ronald J. Stern) Abstract. The retrosection theorem says that any hyperbolic or Riemann sur- face can be uniformized by a Schottky group. We generalize this theorem to the case of hyperbolic 2-orbifolds by giving necessary and sufficient conditions for a hyperbolic 2-orbifold, in terms of its signature, to admit a uniformization by a Kleinian group which is a finite extension of a Schottky group. Equiva- lent^, the conditions characterize those hyperbolic 2-orbifolds which occur as the boundary of a handlebody orbifold, that is, the quotient of a handlebody by a finite group action. 1. Introduction Let F be a Fuchsian group, that is a discrete group of Möbius transforma- tions—or equivalently, hyperbolic isometries—acting on the upper half space or the interior of the unit disk H2 (Poincaré model of the hyperbolic plane). We shall always assume that F has compact quotient tf = H2/F which is a hyperbolic 2-orbifold with signature (g;nx,...,nr); here g denotes the genus of the quotient which is a closed orientable surface, and nx, ... , nr are the orders of the branch points (the singular set of the orbifold) of the branched covering H2 -» H2/F. Then also F has signature (g;nx,... , nr), and (2 - 2g - £-=1(l - 1/«/)) < 0 (see [12] resp. [15] for information about orbifolds resp. Fuchsian groups). In case r — 0, or equivalently, if the Fuch- sian group F is without torsion, the quotient H2/F is a hyperbolic or Riemann surface without branch points.
    [Show full text]
  • Hyperbolic Geometry, Fuchsian Groups, and Tiling Spaces
    HYPERBOLIC GEOMETRY, FUCHSIAN GROUPS, AND TILING SPACES C. OLIVARES Abstract. Expository paper on hyperbolic geometry and Fuchsian groups. Exposition is based on utilizing the group action of hyperbolic isometries to discover facts about the space across models. Fuchsian groups are character- ized, and applied to construct tilings of hyperbolic space. Contents 1. Introduction1 2. The Origin of Hyperbolic Geometry2 3. The Poincar´eDisk Model of 2D Hyperbolic Space3 3.1. Length in the Poincar´eDisk4 3.2. Groups of Isometries in Hyperbolic Space5 3.3. Hyperbolic Geodesics6 4. The Half-Plane Model of Hyperbolic Space 10 5. The Classification of Hyperbolic Isometries 14 5.1. The Three Classes of Isometries 15 5.2. Hyperbolic Elements 17 5.3. Parabolic Elements 18 5.4. Elliptic Elements 18 6. Fuchsian Groups 19 6.1. Defining Fuchsian Groups 20 6.2. Fuchsian Group Action 20 Acknowledgements 26 References 26 1. Introduction One of the goals of geometry is to characterize what a space \looks like." This task is difficult because a space is just a non-empty set endowed with an axiomatic structure|a list of rules for its points to follow. But, a priori, there is nothing that a list of axioms tells us about the curvature of a space, or what a circle, triangle, or other classical shapes would look like in a space. Moreover, the ways geometry manifests itself vary wildly according to changes in the axioms. As an example, consider the following: There are two spaces, with two different rules. In one space, planets are round, and in the other, planets are flat.
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
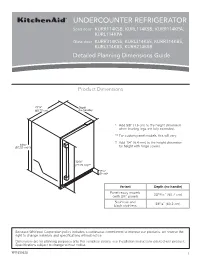
  • Dimension Guide
    UNDERCOUNTER REFRIGERATOR Solid door KURR114KSB, KURL114KSB, KURR114KPA, KURL114KPA Glass door KURR314KSS, KURL314KSS, KURR314KBS, KURL314KBS, KURR214KSB Detailed Planning Dimensions Guide Product Dimensions 237/8” Depth (60.72 cm) (no handle) * Add 5/8” (1.6 cm) to the height dimension when leveling legs are fully extended. ** For custom panel models, this will vary. † Add 1/4” (6.4 mm) to the height dimension 343/8” (87.32 cm)*† for height with hinge covers. 305/8” (77.75 cm)** 39/16” (9 cm)* Variant Depth (no handle) Panel ready models 2313/16” (60.7 cm) (with 3/4” panel) Stainless and 235/8” (60.2 cm) black stainless Because Whirlpool Corporation policy includes a continuous commitment to improve our products, we reserve the right to change materials and specifications without notice. Dimensions are for planning purposes only. For complete details, see Installation Instructions packed with product. Specifications subject to change without notice. W11530525 1 Panel ready models Stainless and black Dimension Description (with 3/4” panel) stainless models A Width of door 233/4” (60.3 cm) 233/4” (60.3 cm) B Width of the grille 2313/16” (60.5 cm) 2313/16” (60.5 cm) C Height to top of handle ** 311/8” (78.85 cm) Width from side of refrigerator to 1 D handle – door open 90° ** 2 /3” (5.95 cm) E Depth without door 2111/16” (55.1 cm) 2111/16” (55.1 cm) F Depth with door 2313/16” (60.7 cm) 235/8” (60.2 cm) 7 G Depth with handle ** 26 /16” (67.15 cm) H Depth with door open 90° 4715/16” (121.8 cm) 4715/16” (121.8 cm) **For custom panel models, this will vary.
    [Show full text]
  • Spectral Dimensions and Dimension Spectra of Quantum Spacetimes
    PHYSICAL REVIEW D 102, 086003 (2020) Spectral dimensions and dimension spectra of quantum spacetimes † Michał Eckstein 1,2,* and Tomasz Trześniewski 3,2, 1Institute of Theoretical Physics and Astrophysics, National Quantum Information Centre, Faculty of Mathematics, Physics and Informatics, University of Gdańsk, ulica Wita Stwosza 57, 80-308 Gdańsk, Poland 2Copernicus Center for Interdisciplinary Studies, ulica Szczepańska 1/5, 31-011 Kraków, Poland 3Institute of Theoretical Physics, Jagiellonian University, ulica S. Łojasiewicza 11, 30-348 Kraków, Poland (Received 11 June 2020; accepted 3 September 2020; published 5 October 2020) Different approaches to quantum gravity generally predict that the dimension of spacetime at the fundamental level is not 4. The principal tool to measure how the dimension changes between the IR and UV scales of the theory is the spectral dimension. On the other hand, the noncommutative-geometric perspective suggests that quantum spacetimes ought to be characterized by a discrete complex set—the dimension spectrum. We show that these two notions complement each other and the dimension spectrum is very useful in unraveling the UV behavior of the spectral dimension. We perform an extended analysis highlighting the trouble spots and illustrate the general results with two concrete examples: the quantum sphere and the κ-Minkowski spacetime, for a few different Laplacians. In particular, we find that the spectral dimensions of the former exhibit log-periodic oscillations, the amplitude of which decays rapidly as the deformation parameter tends to the classical value. In contrast, no such oscillations occur for either of the three considered Laplacians on the κ-Minkowski spacetime. DOI: 10.1103/PhysRevD.102.086003 I.
    [Show full text]
  • Zero-Dimensional Symmetry
    Snapshots of modern mathematics № 3/2015 from Oberwolfach Zero-dimensional symmetry George Willis This snapshot is about zero-dimensional symmetry. Thanks to recent discoveries we now understand such symmetry better than previously imagined possible. While still far from complete, a picture of zero-dimen- sional symmetry is beginning to emerge. 1 An introduction to symmetry: spinning globes and infinite wallpapers Let’s begin with an example. Think of a sphere, for example a globe’s surface. Every point on it is specified by two parameters, longitude and latitude. This makes the sphere a two-dimensional surface. You can rotate the globe along an axis through the center; the object you obtain after the rotation still looks like the original globe (although now maybe New York is where the Mount Everest used to be), meaning that the sphere has rotational symmetry. Each rotation is prescribed by the latitude and longitude where the axis cuts the southern hemisphere, and by an angle through which it rotates the sphere. 1 These three parameters specify all rotations of the sphere, which thus has three-dimensional rotational symmetry. In general, a symmetry may be viewed as being a transformation (such as a rotation) that leaves an object looking unchanged. When one transformation is followed by a second, the result is a third transformation that is called the product of the other two. The collection of symmetries and their product 1 Note that we include the rotation through the angle 0, that is, the case where the globe actually does not rotate at all. 1 operation forms an algebraic structure called a group 2 .
    [Show full text]
  • Hyperbolic Geometry of Riemann Surfaces
    3 Hyperbolic geometry of Riemann surfaces By Theorem 1.8.8, all hyperbolic Riemann surfaces inherit the geometry of the hyperbolic plane. How this geometry interacts with the topology of a Riemann surface is a complicated business, and beginning with Section 3.2, the material will become more demanding. Since this book is largely devoted to the study of Riemann surfaces, a careful study of this interaction is of central interest and underlies most of the remainder of the book. 3.1 Fuchsian groups We saw in Proposition 1.8.14 that torsion-free Fuchsian groups and hyper- bolic Riemann surfaces are essentially the same subject. Most such groups and most such surfaces are complicated objects: usually, a Fuchsian group is at least as complicated as a free group on two generators. However, in a few exceptional cases Fuchsian groups are not complicated, whether they have torsion or not. Such groups are called elementary;we classify them in parts 1–3 of Proposition 3.1.2. Part 4 concerns the com- plicated case – the one that really interests us. Notationin 3.1.1 If A is a subset of a group G, we denote by hAi the subgroup generated by A. Propositionin 3.1.2 (Fuchsian groups) Let be a Fuchsian group. 1. If is nite, it is a cyclic group generated by a rotation about a point by 2/n radians, for some positive integer n. 2. If is innite but consists entirely of elliptic and parabolic ele- ments, then it is innite cyclic, is generated by a single parabolic element, and contains no elliptic elements.
    [Show full text]
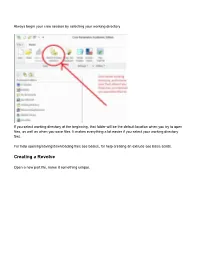
  • Creating a Revolve
    Always begin your creo session by selecting your working directory If you select working directory at the beginning, that folder will be the default location when you try to open files, as well as when you save files. It makes everything a lot easier if you select your working directory first. For help opening/saving/downloading files see basics, for help creating an extrude see basic solids. Creating a Revolve Open a new part file, name it something unique. Choose a plane to sketch on Go to sketch view (if you don’t know where that is see Basic Solids) Move your cursor so the centerline snaps to the horizontal line as shown above You may now begin your sketch I have just sketched a random shape Sketch Tips: ● Your shape MUST be closed ● If you didn’t put a centerline in, you will get radial instead of diameter dimensions (in general this is bad) ● Remember this is being revolved so you are only sketching the profile on one side of the center line. If you need to put in diameter dimensions: Click normal, click the line or point you want the dimension for, click the centerline, and click the same line/point that you clicked the first time AGAIN, and then middle mouse button where you want the dimension to be placed. After your sketch is done, click the checkmark to get out of sketch, then click the checkmark again to complete the revolve The part in the sketch will look like this: .
    [Show full text]
  • Riemann Surfaces As Orbit Spaces of Fuchsian Groups
    Can. J. Math., Vol. XXIV, No. 4, 1972, pp. 612-616 RIEMANN SURFACES AS ORBIT SPACES OF FUCHSIAN GROUPS M. J. MOORE 1. Introduction. A Fuchsian group is a discrete subgroup of the hyperbolic group, L.F. (2, R), of linear fractional transformations w = i—7 (a> b> c> d real, ad — be = 1), cz + a each such transformation mapping the complex upper half plane D into itself. If T is a Fuchsian group, the orbit space D/T has an analytic structure such that the projection map p: D —» D/T, given by p(z) = Yz, is holomorphic and D/Y is then a Riemann surface. If N is a normal subgroup of a Fuchsian group T, then iV is a Fuchsian group and 5 = D/N is a Riemann surface. The factor group, G = T/N, acts as a group of automorphisms (biholomorphic self-transformations) of 5 for, if y e Y and z e D, then yN e G, Nz e S, and (yN) (Nz) = Nyz. This is easily seen to be independent of the choice of y in its iV-coset and the choice of z in its iV-orbit. Conversely, if 5 is a compact Riemann surface, of genus at least two, then S can be identified with D/K, where K is a Fuchsian group acting without fixed points in D. D is the universal covering space of 5 and K is isomorphic to the fundamental group of S. We shall call a Fuchsian group which acts without fixed points in D, a Fuchsian surface group.
    [Show full text]
  • ON the COHOMOLOGY of FUCHSIAN GROUPS by S
    ON THE COHOMOLOGY OF FUCHSIAN GROUPS by S. J. PATTERSON (Received 12 September, 1974; revised 15 May, 1975) 1. Introduction. The object of this paper is to redevelop the classical theory of multi- pliers of Fuchsian groups [16] and to attempt a classification. The language which appears most appropriate is that of group extensions and the cohomology of groups. This viewpoint is not entirely novel [12] but the entire theory has never been based on it before. A Fuchsian group G is a discrete subgroup of PSL(2 ; R). We shall further assume that G is finitely generated and that PSL(2 ; R)/G has finite volume. We shall begin by investi- gating the extensions of PSL(2 ; R). These induce extensions of G. On the other hand G can be given explicitly by generators and relations. So, in principle at any rate, its extensions can be classified from the point of view of group theory. There is then the basic problem of relating these two approaches. In the case that G has no elliptic elements, this identification can be carried out explicitly by using Chern characters to identify algebraically and geometrically defined objects. A partial extension to groups with elliptic elements can be made using the transfer homomor- phism of group cohomology. As a first application, we consider the question as to when G can be lifted to SL(2 ; R). We prove again a theorem of Petersson ([17]) and Bers ([1]) (itself the answer to a question of Siegel ([22])). Bers' proof was an application of the theory of moduli of Riemann surfaces; ours, being intrinsic, can be considered rather more satisfying.
    [Show full text]
  • Why Observable Space Is Three Dimensional
    Adv. Studies Theor. Phys., Vol. 8, 2014, no. 17, 689 – 700 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/astp.2014.4675 Why Observable Space Is Solely Three Dimensional Mario Rabinowitz Armor Research, 715 Lakemead Way Redwood City, CA 94062-3922, USA Copyright © 2014 Mario Rabinowitz. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract Quantum (and classical) binding energy considerations in n-dimensional space indicate that atoms (and planets) can only exist in three-dimensional space. This is why observable space is solely 3-dimensional. Both a novel Virial theorem analysis, and detailed classical and quantum energy calculations for 3-space circular and elliptical orbits indicate that they have no orbital binding energy in greater than 3-space. The same energy equation also excludes the possibility of atom-like bodies in strictly 1 and 2-dimensions. A prediction is made that in the search for deviations from r2 of the gravitational force at sub-millimeter distances such a deviation must occur at < ~ 1010m (or < ~1012 m considering muoniom), since atoms would disintegrate if the curled up dimensions of string theory were larger than this. Callender asserts that the often-repeated claim in previous work that stable orbits are possible in only three dimensions is not even remotely established. The binding energy analysis herein avoids the pitfalls that Callender points out, as it circumvents stability issues. An uncanny quantum surprise is present in very high dimensions.
    [Show full text]