COMPRESSED NONNEGATIVE MATRIX FACTORIZATION IS FAST and ACCURATE Mariano Tepper, Guillermo Sapiro
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CAPTAIN MARVEL # History: the History of the Drug Supplier and Cult Leader Known As the Black Talon Is Currently Unrevealed
BLACK TALON Villain Real Name: Unrevealed. Occupation: Cult leader, drug supplier. Identity: Secret. Legal Status: Citizen of the United States (Puerto Rico) with no criminal record. Other Aliases: The Living Loa, "Chicken-head". Place of Birth: Presumably somewhere in Puerto Rico. Marital Status: Single. Known Relatives: None. Group Affiliation: Head of his own voodoo cult. Base of Operations: A sugar/cocaine plantation in Puerto Rico. First Post-Reboot Appearance: CAPTAIN MARVEL # History: The history of the drug supplier and cult leader known as the Black Talon is currently unrevealed. At some point in the past, he learned the art of voodoo and put that talent to work in raising zombies to work a farm – in reality a Colonial-era plantation he either inherited or acquired – where he grew marijuana and coca plants alongside sugar cane (the plantation's legitimate crop). At the same time, he began a cult of voodoo worshippers who revered him as a "living loa" (the "loa" being the spirits or gods – the line between them is often blurred – invoked by voodoo practitioners.). In time, he became one of the largest suppliers of marijuana and cocaine in the Caribbean, with contacts in Miami, Havana, San Juan, and New Orleans. Black Talon's operations first came into conflict with the current generation of superheroes when a rocket launched by NASA carrying a payload of a powerful nerve gas to be disposed of by being sent into the sun was sabotaged and landed off the coast from his plantation. This brought him into conflict with Captain Marvel, who was under orders from his superior, Colonel Yon-Rogg, to release the nerve gas on a human settlement (see Captain Marvel; Yon-Rogg). -

Fantastic Four Volume 3: Back in Blue Free
FREE FANTASTIC FOUR VOLUME 3: BACK IN BLUE PDF Leonard Kirk,James Robinson | 120 pages | 05 May 2015 | Marvel Comics | 9780785192206 | English | New York, United States Fantastic Four Vol. 3: Back in Blue (Trade Paperback) | Comic Issues | Comic Books | Marvel Uh-oh, it looks like your Internet Explorer is out of date. For a better shopping experience, please upgrade now. Javascript is not enabled in your browser. Enabling JavaScript in your browser will allow you to Fantastic Four Volume 3: Back in Blue all the features of our site. Learn how to enable JavaScript on your browser. Home 1 Books 2. Add to Wishlist. Sign in to Purchase Instantly. Explore Now. Buy As Gift. Overview Collects Fantastic Four The Fantastic Four must deal with the Council of Dooms, who treat that event as their nativity - and who have trevaled there to witness it! To make matters worse, Mr. Fantastic's sickness spreads to the Fantastic Four Volume 3: Back in Blue - and someone may be behind the illness that's befallen the First Family! The team must mastermind a planetary heist for technology that could save their lives, but spacetime has had enough of their traveling back and forth across it - and they soon find themselves trapped in a universe where the only five things left alive are themselves Product Details About the Author. About the Author. He lives in Portland, OR. Related Searches. The time-displaced young X-Men continue to adjust to a present day that's simultaneously more awe-inspiring The time-displaced young X-Men continue to adjust to a present day that's simultaneously more awe-inspiring and more disturbing than any future the young heroes had ever imagined for themselves. -

Customer Order Form
#376 | JAN20 PREVIEWS world.com Name: ORDERS DUE JAN 18 THE COMIC SHOP’S CATALOG PREVIEWSPREVIEWS CUSTOMER ORDER FORM CUSTOMER 601 7 Jan20 Cover ROF and COF.indd 1 12/5/2019 4:59:33 PM Jan20 Ad DST Catwoman.indd 1 12/5/2019 3:43:15 PM PREMIER COMICS DECORUM #1 IMAGE COMICS 50 MIRKA ANDOLFO’S MERCY #1 IMAGE COMICS 54 X-RAY ROBOT #1 DARK HORSE COMICS 94 STARSHIP DOWN #1 DARK HORSE COMICS 96 ROBIN 80TH ANNIVERSARY 100-PAGE SPECTACULAR #1 DC COMICS DCP-1 STRANGE ADVENTURES #1 DC COMICS DCP-3 TRANSFORMERS VS. TERMINATOR #1 IDW PUBLISHING 130 SONIC THE HEDGEHOG ANNUAL 2020 IDW PUBLISHING 137 SPIDER-WOMAN #1 MARVEL COMICS MP-8 KILLING RED SONJA #1 DYNAMITE ENTERTAINMENT 168 KING OF NOWHERE #1 BOOM! STUDIOS 204 Jan20 Gem Page ROF COF.indd 1 12/5/2019 10:58:38 AM COMIC BOOKS & GRAPHIC NOVELS Vampire State Building HC l ABLAZE The Man Who Effed Up Time #1 l AFTERSHOCK COMICS Second Coming Volume 1 TP l AHOY COMICS The Spirit 80th Anniversary Celebration TP l CLOVER PRESS Marvel: We Are Super Heroes HC l DK PUBLISHING CO FEATURED ITEMS COMIC BOOKS & GRAPHIC NOVELS 1 Amazing Spider-Man: My Mighty Marvel First Book Board Book l ABRAMS APPLESEED Captain America: My Mighty Marvel First Book Board Book l ABRAMS APPLESEED Artemis and the Assassin #1 l AFTERSHOCK COMICS Billionaire Island #1 l AHOY COMICS Hatchet: Unstoppable Horror #1 l AMERICAN MYTHOLOGY PRODUCTIONS 1 Cayrel’s Ring HC l A WAVE BLUE WORLD INC Resistance #1 l ARTISTS WRITERS & ARTISANS INC Doctor Who: At Childhood’s End HC l BBC BOOKS Tarot: Witch of the Black Rose #121 l BROADSWORD COMICS Butcher Knight TP l CLOVER PRESS, LLC Dragon Hoops HC l :01 FIRST SECOND The Fire Never Goes Out: A Memoir In Pictures HC l HARPER TEEN Hexagon #1 l IMPACT THEORY, LLC Star Trek: Kirk-Fu Manual HC l INSIGHT EDITIONS Dryad #1 l ONI PRESS The Mythics Vol. -

Marvel-Phile
by Steven E. Schend and Dale A. Donovan Lesser Lights II: Long-lost heroes This past summer has seen the reemer- 3-D MAN gence of some Marvel characters who Gestalt being havent been seen in action since the early 1980s. Of course, Im speaking of Adam POWERS: Warlock and Thanos, the major players in Alter ego: Hal Chandler owns a pair of the cosmic epic Infinity Gauntlet mini- special glasses that have identical red and series. Its great to see these old characters green images of a human figure on each back in their four-color glory, and Im sure lens. When Hal dons the glasses and focus- there are some great plans with these es on merging the two figures, he triggers characters forthcoming. a dimensional transfer that places him in a Nostalgia, the lowly terror of nigh- trancelike state. His mind and the two forgotten days, is alive still in The images from his glasses of his elder broth- MARVEL®-Phile in this, the second half of er, Chuck, merge into a gestalt being our quest to bring you characters from known as 3-D Man. the dusty pages of Marvel Comics past. As 3-D Man can remain active for only the aforementioned miniseries is showing three hours at a time, after which he must readers new and old, just because a char- split into his composite images and return acter hasnt been seen in a while certainly Hals mind to his body. While active, 3-D doesnt mean he lacks potential. This is the Mans brain is a composite of the minds of case with our two intrepid heroes for this both Hal and Chuck Chandler, with Chuck month, 3-D Man and the Blue Shield. -

Heroclix Bestand 16-10-2012
Heroclix Liste Infinity Challenge Infinity Gauntlet Figure Name Gelb Blau Rot Figure Name Gelb Blau Rot Silber und Bronze Adam Warlock 1 SHIELD Agent 1 2 3 Mr. Hyde 109 110 111 Vision 139 In-Betweener 2 SHIELD Medic 4 5 6 Klaw 112 113 114 Quasar 140 Champion 3 Hydra Operative 7 8 9 Controller 115 116 117 Thanos 141 Gardener 4 Hydra Medic 10 11 12 Hercules 118 119 120 Nightmare 142 Runner 5 Thug 13 14 15 Rogue 121 122 123 Wasp 143 Collector 6 Henchman 16 17 18 Dr. Strange 124 125 126 Elektra 144 Grandmaster 7 Skrull Agent 19 20 21 Magneto 127 128 129 Professor Xavier 145 Infinity Gauntlet 101 Skrull Warrior 22 23 24 Kang 130 131 132 Juggernaut 146 Soul Gem S101 Blade 25 26 27 Ultron 133 134 135 Cyclops 147 Power Gem S102 Wolfsbane 28 29 30 Firelord 136 137 138 Captain America 148 Time Gem S103 Elektra 31 32 33 Wolverine 149 Space Gem S104 Wasp 34 35 36 Spider-Man 150 Reality Gem S105 Constrictor 37 38 39 Marvel 2099 Gabriel Jones 151 Mind Gem S106 Boomerang 40 41 42 Tia Senyaka 152 Kingpin 43 44 45 Hulk 1 Operative 153 Vulture 46 47 48 Ravage 2 Medic 154 Jean Grey 49 50 51 Punisher 3 Knuckles 155 Hammer of Thor Hobgoblin 52 53 54 Ghost Rider 4 Joey the Snake 156 Fast Forces Sabretooth 55 56 57 Meanstreak 5 Nenora 157 Hulk 58 59 60 Junkpile 6 Raksor 158 Fandral 1 Puppet Master 61 62 63 Doom 7 Blade 159 Hogun 2 Annihilus 64 65 66 Rahne Sinclair 160 Volstagg 3 Captain America 67 68 69 Frank Schlichting 161 Asgardian Brawler 4 Spider-Man 70 71 72 Danger Room Fred Myers 162 Thor 5 Wolverine 73 74 75 Wilson Fisk 163 Loki 6 Professor Xavier 76 -

A Player's Guide Part 1
A Player’s Guide Effective: 7/1/2012 Any game elements indicated with the † symbol may only be used with the Golden Age format. Any game elements indicated with the ‡ symbol may only be used with the Star Trek: Tactics game. Items labeled with a are available exclusively through Print-and-Play. Any page references refer to the HeroClix 2011 2012 Core Rulebook. Part 1 – Clarifications Section 1: Rulebook 3 Section 2: Powers 7 Section 3: Abilities 9 Section 4: Characters and Special Powers 11 Section 5: Special Characters 27 Section 6: Team Abilities 29 Section 7: Additional Team Abilities 31 Section 8: Battlefield Conditions 33 Section 9: Feats 35 Section 10: Objects 41 Section 11: Maps 43 Section 12: Resources 47 Part 2 – Current Wordings Section 13: Powers 49 Section 14: Abilities 53 Section 15: Characters and Special Powers 57 Section 16: Team Abilities 141 Section 17: Additional Team Abilities 145 Section 18: Battlefield Conditions 151 Section 19: Feats 155 Section 20: Objects 167 Section 21: Maps 171 Section 22: Resources 175 How To Use This Document This document is divided into two parts. The first part details every clarification that has been made in HeroClix for all game elements. These 48 pages are the minimal requirements for being up to date on all HeroClix rulings. Part two is a reference guide for players and judges who often need to know the latest text of any given game element. Any modification listed in part two is also listed in part one; however, in part two the modifications will be shown as fully completed elements of game text. -

X-Men, Dragon Age, and Religion: Representations of Religion and the Religious in Comic Books, Video Games, and Their Related Media Lyndsey E
Georgia Southern University Digital Commons@Georgia Southern University Honors Program Theses 2015 X-Men, Dragon Age, and Religion: Representations of Religion and the Religious in Comic Books, Video Games, and Their Related Media Lyndsey E. Shelton Georgia Southern University Follow this and additional works at: https://digitalcommons.georgiasouthern.edu/honors-theses Part of the American Popular Culture Commons, International and Area Studies Commons, and the Religion Commons Recommended Citation Shelton, Lyndsey E., "X-Men, Dragon Age, and Religion: Representations of Religion and the Religious in Comic Books, Video Games, and Their Related Media" (2015). University Honors Program Theses. 146. https://digitalcommons.georgiasouthern.edu/honors-theses/146 This thesis (open access) is brought to you for free and open access by Digital Commons@Georgia Southern. It has been accepted for inclusion in University Honors Program Theses by an authorized administrator of Digital Commons@Georgia Southern. For more information, please contact [email protected]. X-Men, Dragon Age, and Religion: Representations of Religion and the Religious in Comic Books, Video Games, and Their Related Media An Honors Thesis submitted in partial fulfillment of the requirements for Honors in International Studies. By Lyndsey Erin Shelton Under the mentorship of Dr. Darin H. Van Tassell ABSTRACT It is a widely accepted notion that a child can only be called stupid for so long before they believe it, can only be treated in a particular way for so long before that is the only way that they know. Why is that notion never applied to how we treat, address, and present religion and the religious to children and young adults? In recent years, questions have been continuously brought up about how we portray violence, sexuality, gender, race, and many other issues in popular media directed towards young people, particularly video games. -

Marvel Comics Jan20 0795 Strange Academy #1 $4.99
MARVEL COMICS JAN20 0795 STRANGE ACADEMY #1 $4.99 JAN20 0796 STRANGE ACADEMY #1 CHARACTER SPOTLIGHT VAR $4.99 JAN20 0797 STRANGE ACADEMY #1 RAMOS DESIGN VAR $4.99 JAN20 0798 STRANGE ACADEMY #1 JS CAMPBELL VAR $4.99 JAN20 0800 STRANGE ACADEMY #1 YOUNG VAR $4.99 JAN20 0802 SPIDER-WOMAN #1 YOON CLASSIC CVR $4.99 JAN20 0803 SPIDER-WOMAN #1 YOON NEW COSTUME CVR $4.99 JAN20 0804 SPIDER-WOMAN #1 ARTGERM VAR $4.99 JAN20 0807 SPIDER-WOMAN #1 RON LIM VAR $4.99 JAN20 0810 SPIDER-WOMAN #1 JS CAMPBELL VAR $4.99 JAN20 0811 SPIDER-WOMAN #1 NAUCK VILLAINS VAR $4.99 JAN20 0814 SPIDER-WOMAN #1 BLANK VAR $4.99 JAN20 0815 SPIDER-WOMAN #1 MR GARCIN VAR $4.99 JAN20 0816 SPIDER-MAN NOIR #1 (OF 5) $3.99 JAN20 0817 SPIDER-MAN NOIR #1 (OF 5) RON LIM VAR $3.99 JAN20 0820 HELLIONS #1 DX $4.99 JAN20 0821 HELLIONS #1 PORTACIO VAR DX $4.99 JAN20 0826 CABLE #1 DX $4.99 JAN20 0830 CABLE #1 YOUNG VAR DX $4.99 JAN20 0831 CABLE #1 BLACK BLANK VAR DX $4.99 JAN20 0832 WOLVERINE #2 DX $3.99 JAN20 0834 WOLVERINE #2 PAREL SPIDER-WOMAN VAR DX $3.99 JAN20 0836 INCREDIBLE HULK #182 FACSIMILE EDITION $3.99 JAN20 0837 THOR #229 FACSIMILE EDITION $3.99 JAN20 0838 X-MEN GIANT SIZE MAGNETO #1 DX $4.99 JAN20 0839 X-MEN GIANT SIZE MAGNETO #1 RIBIC VAR DX $4.99 JAN20 0840 X-MEN FANTASTIC FOUR #3 (OF 4) $3.99 JAN20 0842 X-MEN FANTASTIC FOUR #3 (OF 4) HETRICK FLOWER VAR $3.99 JAN20 0843 X-MEN #8 DX $3.99 JAN20 0845 X-MEN #9 DX $3.99 JAN20 0846 EXCALIBUR #8 DX $3.99 JAN20 0847 EXCALIBUR #9 DX $3.99 JAN20 0849 NEW MUTANTS #9 DX $3.99 JAN20 0851 X-FORCE #9 DX $3.99 JAN20 0853 MARAUDERS #9 DX -

Vs System 2PCG Rules
Ages 14+ “If you want to fly to the stars, then you pilot the ship! Count me out! You know we haven’t done enough research into the effect of cosmic rays!” – Ben Grimm, to Reed Richards, Fantastic Four #1 The Story So Far… For the past few years, players have fought epic battles across the Earth and beyond – recruiting superheroes and supervillains as well as horrifying aliens, deadly hunters, government agents, supernatural monsters, and vampires! Now the first family of super teams is joining the fight! Will you join the Fantastic Four in their battle to protect the earth? Or will you join the multitudes of their enemies bent on Earth’s conquest? What is the Vs. System® 2PCG®? The Vs. System® 2PCG® is a card game where 2-4 players each build a deck of Characters, Plot Twists, Locations, and Equipment to try to defeat their opponents. Each Vs. System® 2PCG® product comes with a full playset of cards. Game Contents • 200 Cards • Assorted Counters • This Rulebook Issues and Giant-Sized Issues The Vs. System® 2PCG® releases a new expansion almost every month. “Issues” are small expansions that include 55 cards. “Giant- Sized Issues” are large expansions, which include 200 cards, and are the perfect way for new players to dive into the game. This Giant-Sized Issue adds one new Good team and one new Evil team to the game: the Fantastic ( ) and the Frightful ( ). And the next two Issues add even more cards for both teams, making it a 3-Issue Arc. 1 If you’re familiar with the Vs. -

MHRP Hero Datafiles
ARMOR PP Affiliations Solo Buddy Team STRESS / TRAUMA Distinctions Dutiful Student Heroic Ambition or Technophile +1 PP Power Sets PSYCHIC EXO-ARMOR Superhuman Durability Superhuman Strength SFX: Ancestral Boost. Step up or double a Psychic Exo-Armor die for that Scene, or spend 1 PP to do both. Take your second-highest rolling die of each subsequent P action or reaction as emotional or physical stress. SFX: Memory Surge. Use your current emotional stress die as your effect die, then step 4 up your emotional stress by +1. 6 SFX: Invulnerable. Spend 1 PP to ignore physical stress or trauma results unless caused by light-based attacks. 8 Limit: Conscious Activation. While stressed out, asleep, or unconscious, shutdown Psychic Exo-Armor. Recover Psychic Exo-Armor when you recover that stress 10 or wake up. If you take emotional trauma, shutdown Psychic Exo-Armor until you recover that trauma. 12 Limit: Mutant. Earn 1 PP when affected by mutant-specific Milestones and tech. M 4 6 Specialties Combat Expert Science Expert 8 Tech Expert 10 [You may convert Expert d8 to 2d6, or Master d10 to 2d8 or 3d6] 12 E 4 Milestones FOR MY ANCESTORS 6 1 XP when you first use your Ancestral Boost SFX. 3 XP when you make your Japanese heritage the subject of an argument or 8 confrontation. 10 XP when you either embrace your heritage completely or deny it. 10 ONE OF THE TEAM 12 1 XP when you give support to another hero. 3 XP when you’re given an official place on a team. -
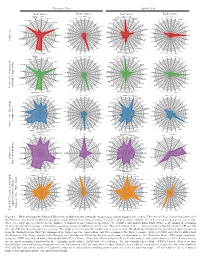
Fantastic Four Spider-Man Left Factor Right Factor Left Factor Right Factor
Fantastic Four Spider-Man Left factor Right factor Left factor Right factor RICHARDS SHE-HULK M/TIO@ MEPHV. SPIDER-MAN STACY SENSM SM:FA FRANKLIN B MICRO SPIDER-MAN CLONE GWEN SM:PL SILVER SURFER M/TIO THOMPSON S-M PP ROBERTSON EUGENE FLA SPECSM MS. MARVEL II RANDY M/SHSW URICH PWJ ST BEN UTSM SUB-MARINER ROBERTSON M/FAN JOE PPTSS@ MR. FANTASTIC WATSON SVTU ANNA UTSM:SE PARKER THING IW MAY PPTSS WATSON-PARKER TB MARY WOSM MEDUSA OSBORN IM2 LIZ ALLAN PPSM2 BLACK BOLT A BLACK CAT ASM OSBORN MASTERS HR:R HARRY MSM ALICIA REIS CUSHING A@ KATE ASM2 Active set CRYSTAL H2 LEEDS M/TU@ NED ASM ASM:FO LYJA LAZERFIST DAREDEVIL GAL LEEDS M/TU2 BETTY BRANT DR. DOOM DAZZ DR. OCTOPUS ASM@ KARNAK FFV.X KINGPIN M/TU DF GRANT ASMU GLORIA GLORY GORGON FF@ JAMESON GSSH INVISIBLE WOMAN FF MARLA MADISJAMESONGREEN GOBLIN ASMV.W HUMAN TORCH FF3 FF2 J. JONAH GSS-M DB RICHARDS SHE-HULK M/TIO@ MEPHV. SPIDER-MAN STACY SENSM SM:FA FRANKLIN B MICRO SPIDER-MAN CLONE GWEN SM:PL SILVER SURFER M/TIO THOMPSON S-M PP ROBERTSON EUGENE FLA SPECSM MS. MARVEL II RANDY M/SHSW URICH PWJ ST BEN UTSM SUB-MARINER ROBERTSON M/FAN JOE PPTSS@ MR. FANTASTIC WATSON SVTU ANNA UTSM:SE PARKER THING IW MAY PPTSS WATSON-PARKER TB MARY WOSM MEDUSA OSBORN IM2 LIZ ALLAN PPSM2 BLACK BOLT A BLACK CAT ASM OSBORN MASTERS HR:R HARRY MSM ALICIA REIS CUSHING A@ KATE ASM2 CRYSTAL H2 LEEDS M/TU@ NED ASM ASM:FO LYJA LAZERFIST DAREDEVIL GAL LEEDS M/TU2 BETTY BRANT random compression DR. -

A Player's Guide Part 1
A Player’s Guide Effective: 5/1/2012 Items labeled with a are available exclusively through Print-and-Play. Any page references refer to the HeroClix 2011 Core Rulebook. Part 1 – Clarifications Section 1: Rulebook 3 Section 2: Powers 7 Section 3: Abilities 9 Section 4: Characters and Special Powers 11 Section 5: Special Characters 25 Section 6: Team Abilities 27 Section 7: Additional Team Abilities 29 Section 8: Objects 39 Section 9: Maps 41 Section 10: Resources 45 Part 2 – Current Wordings Section 11: Powers 47 Section 12: Abilities 51 Section 13: Characters and Special Powers 53 Section 14: Team Abilities 127 Section 15: Additional Team Abilities 131 Section 16: Objects 151 Section 17: Maps 155 Section 18: Resources 159 How To Use This Document This document is divided into two parts. The first part details every clarification that has been made in HeroClix for all game elements. These 51 pages are the minimal requirements for being up to date on all HeroClix rulings. Part two is a reference guide for players and judges who often need to know the latest text of any given game element. Any modification listed in part two is also listed in part one; however, in part two the modifications will be shown as fully completed elements of game text. [This page is intentionally left blank.] Section 1 Rulebook Errata & Clarifications Damage Taken All page numbers refer to the HeroClix 2011 Core Rulebook. The amount of damage a character takes is always considered the specific number of clicks applied before stopping. If a General character is KO’d or has a game effect that causes the clicking to Many figures have been published with rules detailing their stop, the damage taken is determined accordingly.