DOCSLIB.ORG

VI. Introduction to Generalized Linear Models

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
VI. Introduction to Generalized Linear Models Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 VI. Introduction to Generalized Linear Models Readings for Section VI: Agresti, Chapter 3 We turn our attention now to the topic of modeling a categorical outcome as a function of (possibly) several factors. The framework of generalized linear models unifies a family of regression models that includes (but is not limited to) logistic , Poisson, and linear regression. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Why Model? 1. Structure of the model helps us to describe how various factors are associated with the outcome variable. 2. Size and strength of the effects of primary factor(s) of interest can be explained while adjusting for possible confounding ftfactors. 3. The simultaneous effects of several explanatory variables can be considered, as opposed to just one or two at a time. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Linear Regression: Modeling the Mean Recall that linear regression involves modeling the mean of some outcome variable as a function of one or more explanatory variables. That is, we have a sample Y1,…, Yn of independent measures, where the ith subject in our sample has p explanatory variables xi1, xi2,…, xip, and E(Yi) = μi. The linear reggpression model specifies that … Yi = β0 + β1 xi1 + β2 xi2 + + βp xip + εi, 2 where εi ~ N(0, σ ), for i = 1,…,n. Then E(Yi | xi1, xi2,…, xip) = … 2 β0 + β1 xi1 + + βp xip, and Var(Yi) = σ . This model assumes that the mean of the outcome variable changes linearly with respect to the explanatory variables. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 The Three Components of a Generalized Linear Model Whereas w ith linear regressi on, we mod el th e mean of th e out come variable directly, a generalized linear model is constructed to model the effects of the covariates on a function of the mean. There are hence three parts or components that comprise a generalized linear model: 1. The random component, which specifies the distribution of the outibltcome variable. 2. The systematic component, which represents a function of the covariates that will link to the outcome variable. 3. The link function, which determines how the mean of the outcome variable relates to the covariates. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Generalized Linear Models for Binary Data We have a sample Y1,…, Yn of independent binary outcome measurements. The ith subject in our sample has p explanatory variables xi1, xi2,…, xip. Suppose that P(Yi = 1) = πi and P(Yi = 0) = 1 – πi. Hence, E(Yi) = πi. The random component in this case is clearly binomial. For the purpose of this class, we will always assume that the systematic component is simply a linear combination of the covariates, or … β0 + β1 xi1 + + βp xip. The remaining question is: how do we model πi as a function of the covariates (i.e., what is the link function)? Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Link Functions for the Binomial Distribution … Suppose that we assume that E(Yi) = πi = β0 + β1 xi1 + + βp xip. We call this the identity link. Does this model have any practical shortcomings? Since the systematic component can take on any value, we often prefer us ing a link th at will const rai n πi tthitto the interval lbt between 0 and 1. The so-called logistic or logit link g(πi) = log[πi /(1 – πi)] accomplishes this. There are other links (e.g., the probit), but we will focus mainly on the logit. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Example VI.A Consider a generalized linear model for the Alzheimer’s data from ElIVAExample IV.A. The data are ta bu lated agai n h ere: AD No AD Total ≥ 1 ε4 Allele 308 1296 1604 No ε4 262 3096 3358 Total 570 4392 4962 Note that these data can be viewed as a sample of outcome th measures Y1,…,Y4962, where Yi = 1ifh1 if the i idiidlindividual was diagnosed with AD, and Yi = 0 otherwise. Moreover, we have a th single covariate Xi, which is 1 if the i individual has at least one copy of the APOE ε4 allele, and 0 otherwise. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Example VI.A (cont’d) LtLet πi = P(Yi = 1). No te that thi s i mpli es E(Yi) = πi. TifthTo specify the generalized linear model to explain the relationship between Xi and Yi (that is, between genotype and AD risk), (1) we assume the distribution of Yi (i.e., the random component) is binomial, (2) we employ the standard systematic component, and (3) we use the logit link . This yields the model i logit( i ) log 0 1xi . 1i This happens to be the logistic regression model for these data. The strong assumption is that the log odds of response change linearly with respect to the covariate(s) in the model. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Example VI.A (cont’d) First, how do we interpret the coefficients of this model? What is logit(πi | Xi = 1)? What is logit( πi | Xi = 0)? What is the log odds ratio with respect to AD risk, comparing those with at least one ε4 to those with no ε4? The regression coefficient of a binary covariate in a logistic regression model represents the log odds ratio comparing the group identified as ‘1’ to the group identified as ‘0’. More generally, the coefficient of any arbitrary covariate in a logistic regression mode l represen ts th e l og odd s rati o f or subj ect s wh o diff er b y one unit with respect to the covariate. Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Fitting the Generalized Linear Model for the Alzheimer’s Data in SAS We obtain parameter estimates for a generalized linear model using the method of maximum likelihood – these estimates typically cannot be comp uted in closed form. The following SAS program shows how to read the AD data into SAS, and then obtain a fit for the regression coefficients in the model of Example VI.A. options ls=79 nodate; proc genmod descending; model ad=e4 / dis=bin link=logit data; type3; input e4 ad count; weight count; cards; run; 1 1 308 1 0 1296 0 1 262 0 0 3096 ;; proc sort; by descending ad descending e4; run; proc freq order=data; tables e4*ad / chisq relrisk; weight count; run; SAS Output Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 The FREQ Procedure Table of e4 by ad e4 ad Frequency‚ Percent ‚ Row Pct ‚ Col Pct ‚‚‚‚ 1‚ 0‚ Total ƒƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆ 1 ‚ 308 ‚ 1296 ‚ 1604 ‚ 6.21 ‚ 26.12 ‚ 32.33 ‚ 19.20 ‚ 80.80 ‚ ‚ 54.04 ‚ 29.51 ‚ ƒƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆ 0 ‚ 262 ‚ 3096 ‚ 3358 ‚ 5.28 ‚ 62.39 ‚ 67.67 ‚ 7.80 ‚ 92.20 ‚ ‚ 45.96 ‚ 70.49 ‚ ƒƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆ Total 570 4392 4962 11.4998850000 88.51 100.00 Statistics for Table of e4 by ad Statistic DF Value Prob ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Chi-Square 1 138.7375 <.0001 Like lihoo d Rat io Chi-Square 1 129. 9802 <.0001 Continuity Adj. Chi-Square 1 137.6186 <.0001 Mantel-Haenszel Chi-Square 1 138.7095 <.0001 Phi Coefficient 0.1672 Contingency Coefficient 0.1649 Cramer's V 0.1672 SAS Output (cont’d)Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Fisher's Exact Test ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Cell (1,1) Frequency (F) 308 Left-sided Pr <= F 1.0000 Rig ht-side d Pr >= F 3. 366E-30 Table Probability (P) 6.085E-30 Two-sided Pr <= P 4.889E-30 Estimates of the Relative Risk (Row1/Row2) Type of Study Value 95% Confidence Limits ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Case-Control (Odds Ratio) 2.8083 2.3527 3.3522 Cohort (Col1 Risk) 2.4611 2.1106 2.8697 Cohort (Col2 Risk) 0.8764 0.8540 0.8993 SAS Output (cont’d)Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 The GENMOD Procedure Model Information Data Set WORK.DATA1 Distribution Binomial Link Function Logit Dependent Variable ad Scale Weight Variable count Number of Observations Read 4 Number of Observations Used 4 Sum of Weights 4962 Number of Events 2 Number of Trials 4 Response Profile Ordered Total Value ad Frequency 1 1 570 2 0 4392 PROC GENMOD is modeling the probability that ad='1'. Criteria For Assessing Goodness Of Fit Criterion DF Value Value/DF Deviance 2 3408.7579 1704.3790 Scaled Deviance 2 3408.7579 1704.3790 Pearson Chi-Square 2 4962.0000 2481.0000 Scaled Pearson X2 2 4962.0000 2481.0000 Log Likelihood -1704.3790 Algorithm converged. SAS Output (cont’d)Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Analysis Of Parameter Estimates Standard Wald 95% Chi- Parameter DF Estimate Error Confidence Limits Square Pr > ChiSq Intercept 1 -2. 4695 0. 0643 -259562.5956 -2. 3434 1473. 15 <. 0001 e4 1 1.0326 0.0903 0.8556 1.2096 130.69 <.0001 Scale 0 1.0000 0.0000 1.0000 1.0000 Stat 5120 – Categorical Data Analysis Dr. Corcoran, Fall 2010 Example VI.A (cont’d) ˆ ˆ The SAS ou tput i ndi cat es th at 0 2.4695 and 1 1.0326. According to the fit of the regression model, what are the estimated log odds of AD for someone with no APOE ε4 allele? What are the estimated log odds given for someone with at least one high-risk allele? Wha t is the esti mat ed l og odd s rati o of AD ri sk compari ng ε4 carriers to non-carriers? How does this estimate compare with the sample odds ratio computed using the data in the 2 x 2 table? Stat 5120 – Categorical Data Analysis Dr.
Load more

Recommended publications
  • Goodness of Fit: What Do We Really Want to Know? I
    PHYSTAT2003, SLAC, Stanford, California, September 8-11, 2003 Goodness of Fit: What Do We Really Want to Know? I. Narsky California Institute of Technology, Pasadena, CA 91125, USA Definitions of the goodness-of-fit problem are discussed. A new method for estimation of the goodness of fit using distance to nearest neighbor is described. Performance of several goodness-of-fit methods is studied for time-dependent CP asymmetry measurements of sin(2β). 1. INTRODUCTION of the test is then defined as the probability of ac- cepting the null hypothesis given it is true, and the The goodness-of-fit problem has recently attracted power of the test, 1 − αII , is defined as the probabil- attention from the particle physics community. In ity of rejecting the null hypothesis given the alterna- modern particle experiments, one often performs an tive is true. Above, αI and αII denote Type I and unbinned likelihood fit to data. The experimenter Type II errors, respectively. An ideal hypothesis test then needs to estimate how accurately the fit function is uniformly most powerful (UMP) because it gives approximates the observed distribution. A number of the highest power among all possible tests at the fixed methods have been used to solve this problem in the confidence level. In most realistic problems, it is not past [1], and a number of methods have been recently possible to find a UMP test and one has to consider proposed [2, 3] in the physics literature. various tests with acceptable power functions. For binned data, one typically applies a χ2 statistic There is a long-standing controversy about the con- to estimate the fit quality.
    [Show full text]
  • Linear Regression: Goodness of Fit and Model Selection
    Linear Regression: Goodness of Fit and Model Selection 1 Goodness of Fit I Goodness of fit measures for linear regression are attempts to understand how well a model fits a given set of data. I Models almost never describe the process that generated a dataset exactly I Models approximate reality I However, even models that approximate reality can be used to draw useful inferences or to prediction future observations I ’All Models are wrong, but some are useful’ - George Box 2 Goodness of Fit I We have seen how to check the modelling assumptions of linear regression: I checking the linearity assumption I checking for outliers I checking the normality assumption I checking the distribution of the residuals does not depend on the predictors I These are essential qualitative checks of goodness of fit 3 Sample Size I When making visual checks of data for goodness of fit is important to consider sample size I From a multiple regression model with 2 predictors: I On the left is a histogram of the residuals I On the right is residual vs predictor plot for each of the two predictors 4 Sample Size I The histogram doesn’t look normal but there are only 20 datapoint I We should not expect a better visual fit I Inferences from the linear model should be valid 5 Outliers I Often (particularly when a large dataset is large): I the majority of the residuals will satisfy the model checking assumption I a small number of residuals will violate the normality assumption: they will be very big or very small I Outliers are often generated by a process distinct from those which we are primarily interested in.
    [Show full text]
  • Chapter 2 Simple Linear Regression Analysis the Simple
    Chapter 2 Simple Linear Regression Analysis The simple linear regression model We consider the modelling between the dependent and one independent variable. When there is only one independent variable in the linear regression model, the model is generally termed as a simple linear regression model. When there are more than one independent variables in the model, then the linear model is termed as the multiple linear regression model. The linear model Consider a simple linear regression model yX01 where y is termed as the dependent or study variable and X is termed as the independent or explanatory variable. The terms 0 and 1 are the parameters of the model. The parameter 0 is termed as an intercept term, and the parameter 1 is termed as the slope parameter. These parameters are usually called as regression coefficients. The unobservable error component accounts for the failure of data to lie on the straight line and represents the difference between the true and observed realization of y . There can be several reasons for such difference, e.g., the effect of all deleted variables in the model, variables may be qualitative, inherent randomness in the observations etc. We assume that is observed as independent and identically distributed random variable with mean zero and constant variance 2 . Later, we will additionally assume that is normally distributed. The independent variables are viewed as controlled by the experimenter, so it is considered as non-stochastic whereas y is viewed as a random variable with Ey()01 X and Var() y 2 . Sometimes X can also be a random variable.
    [Show full text]
  • A Study of Some Issues of Goodness-Of-Fit Tests for Logistic Regression Wei Ma
    Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2018 A Study of Some Issues of Goodness-of-Fit Tests for Logistic Regression Wei Ma Follow this and additional works at the DigiNole: FSU's Digital Repository. For more information, please contact [email protected] FLORIDA STATE UNIVERSITY COLLEGE OF ARTS AND SCIENCES A STUDY OF SOME ISSUES OF GOODNESS-OF-FIT TESTS FOR LOGISTIC REGRESSION By WEI MA A Dissertation submitted to the Department of Statistics in partial fulfillment of the requirements for the degree of Doctor of Philosophy 2018 Copyright c 2018 Wei Ma. All Rights Reserved. Wei Ma defended this dissertation on July 17, 2018. The members of the supervisory committee were: Dan McGee Professor Co-Directing Dissertation Qing Mai Professor Co-Directing Dissertation Cathy Levenson University Representative Xufeng Niu Committee Member The Graduate School has verified and approved the above-named committee members, and certifies that the dissertation has been approved in accordance with university requirements. ii ACKNOWLEDGMENTS First of all, I would like to express my sincere gratitude to my advisors, Dr. Dan McGee and Dr. Qing Mai, for their encouragement, continuous support of my PhD study, patient guidance. I could not have completed this dissertation without their help and immense knowledge. I have been extremely lucky to have them as my advisors. I would also like to thank the rest of my committee members: Dr. Cathy Levenson and Dr. Xufeng Niu for their support, comments and help for my thesis. I would like to thank all the staffs and graduate students in my department.
    [Show full text]
  • Testing Goodness Of
    Dr. Wolfgang Rolke University of Puerto Rico - Mayaguez CERN Phystat Seminar 1 Problem statement Hypothesis testing Chi-square Methods based on empirical distribution function Other tests Power studies Running several tests Tests for multi-dimensional data 2 ➢ We have a probability model ➢ We have data from an experiment ➢ Does the data agree with the probability model? 3 Good Model? Or maybe needs more? 4 F: cumulative distribution function 퐻0: 퐹 = 퐹0 Usually more useful: 퐻0: 퐹 ∊ ℱ0 ℱ0 a family of distributions, indexed by parameters. 5 Type I error: reject true null hypothesis Type II error: fail to reject false null hypothesis A: HT has to have a true type I error probability no higher than the nominal one (α) B: probability of committing the type II error (β) should be as low as possible (subject to A) Historically A was achieved either by finding an exact test or having a large enough sample. p value = probability to reject true null hypothesis when repeating the experiment and observing value of test statistic or something even less likely. If method works p-value has uniform distribution. 6 Note above: no alternative hypothesis 퐻1 Different problem: 퐻0: 퐹 = 푓푙푎푡 vs 퐻0: 퐹 = 푙푖푛푒푎푟 → model selection Usually better tests: likelihood ratio test, F tests, BIC etc. Easy to confuse: all GOF papers do power studies, those need specific alternative. Our question: is F a good enough model for data? We want to guard against any alternative. 7 Not again … Actually no, GOF equally important to both (everybody has a likelihood) Maybe more so for Bayesians, no non- parametric methods.
    [Show full text]
  • Measures of Fit for Logistic Regression Paul D
    Paper 1485-2014 SAS Global Forum Measures of Fit for Logistic Regression Paul D. Allison, Statistical Horizons LLC and the University of Pennsylvania ABSTRACT One of the most common questions about logistic regression is “How do I know if my model fits the data?” There are many approaches to answering this question, but they generally fall into two categories: measures of predictive power (like R-square) and goodness of fit tests (like the Pearson chi-square). This presentation looks first at R-square measures, arguing that the optional R-squares reported by PROC LOGISTIC might not be optimal. Measures proposed by McFadden and Tjur appear to be more attractive. As for goodness of fit, the popular Hosmer and Lemeshow test is shown to have some serious problems. Several alternatives are considered. INTRODUCTION One of the most frequent questions I get about logistic regression is “How can I tell if my model fits the data?” Often the questioner is expressing a genuine interest in knowing whether a model is a good model or a not-so-good model. But a more common motivation is to convince someone else--a boss, an editor, or a regulator--that the model is OK. There are two very different approaches to answering this question. One is to get a statistic that measures how well you can predict the dependent variable based on the independent variables. I’ll refer to these kinds of statistics as measures of predictive power. Typically, they vary between 0 and 1, with 0 meaning no predictive power whatsoever and 1 meaning perfect predictions.
    [Show full text]
  • Goodness of Fit of a Straight Line to Data
    5. A linear trend. 10.4 The Least Squares Regression Line LEARNING OBJECTIVES 1. To learn how to measure how well a straight line fits a collection of data. 2. To learn how to construct the least squares regression line, the straight line that best fits a collection of data. 3. To learn the meaning of the slope of the least squares regression line. 4. To learn how to use the least squares regression line to estimate the response variable y in terms of the predictor variablex. Goodness of Fit of a Straight Line to Data Once the scatter diagram of the data has been drawn and the model assumptions described in the previous sections at least visually verified (and perhaps the correlation coefficient r computed to quantitatively verify the linear trend), the next step in the analysis is to find the straight line that best fits the data. We will explain how to measure how well a straight line fits a collection of points by examining how well the line y=12x−1 fits the data set Saylor URL: http://www.saylor.org/books Saylor.org 503 To each point in the data set there is associated an “error,” the positive or negative vertical distance from the point to the line: positive if the point is above the line and negative if it is below theline. The error can be computed as the actual y-value of the point minus the y-value yˆ that is “predicted” by inserting the x-value of the data point into the formula for the line: error at data point (x,y)=(true y)−(predicted y)=y−yˆ The computation of the error for each of the five points in the data set is shown in Table 10.1 "The Errors in Fitting Data with a Straight Line".
    [Show full text]
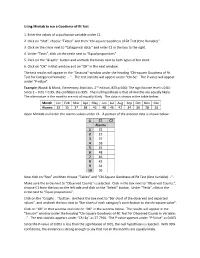
  • Using Minitab to Run a Goodness‐Of‐Fit Test 1. Enter the Values of A
    Using Minitab to run a Goodness‐of‐fit Test 1. Enter the values of a qualitative variable under C1. 2. Click on “Stat”, choose “Tables” and then “Chi‐square Goodness of Fit Test (One Variable)”. 3. Click on the circle next to “Categorical data:” and enter C1 in the box to the right. 4. Under “Tests”, click on the circle next to “Equal proportions”. 5. Click on the “Graphs” button and uncheck the boxes next to both types of bar chart. 6. Click on “OK” in that window and on “OK” in the next window. The test results will appear in the “Sessions” window under the heading “Chi‐square Goodness of Fit Test for Categorical Variable: … ”. The test statistic will appear under “Chi‐Sq”. The P‐value will appear under “P‐value”. Example (Navidi & Monk, Elementary Statistics, 2nd edition, #23 p.566): The significance level is 0.01. Since 1 – 0.01 = 0.99, the confidence is 99%. The null hypothesis is that all months are equally likely. The alternative is the months are not all equally likely. The data is shown in the table below. Month Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Alarms 32 15 37 38 45 48 46 42 34 36 28 26 Open Minitab and enter the alarms values under C1. A portion of the entered data is shown below. ↓ C1 C2 Alarms 1 32 2 15 3 37 4 38 5 45 6 48 7 46 8 42 9 34 10 36 Now click on “Stat” and then choose “Tables” and “Chi‐Square Goodness‐of‐Fit Test (One Variable) …”.
    [Show full text]
  • Goodness-Of-Fit Tests for Parametric Regression Models
    Goodness-of-Fit Tests for Parametric Regression Models Jianqing Fan and Li-Shan Huang Several new tests are proposed for examining the adequacy of a family of parametric models against large nonparametric alternatives. These tests formally check if the bias vector of residuals from parametric ts is negligible by using the adaptive Neyman test and other methods. The testing procedures formalize the traditional model diagnostic tools based on residual plots. We examine the rates of contiguous alternatives that can be detected consistently by the adaptive Neyman test. Applications of the procedures to the partially linear models are thoroughly discussed. Our simulation studies show that the new testing procedures are indeed powerful and omnibus. The power of the proposed tests is comparable to the F -test statistic even in the situations where the F test is known to be suitable and can be far more powerful than the F -test statistic in other situations. An application to testing linear models versus additive models is also discussed. KEY WORDS: Adaptive Neyman test; Contiguous alternatives; Partial linear model; Power; Wavelet thresholding. 1. INTRODUCTION independent observations from a population, Parametric linear models are frequently used to describe Y m4x5 ˜1 ˜ N 401‘ 251 (1.1) the association between a response variable and its predic- D C tors. The adequacy of such parametric ts often arises. Con- ventional methods rely on residual plots against tted values where x is a p-dimensional vector and m4 5 is a smooth regres- sion surface. Let f 4 1 ˆ5 be a given parametri¢ c family. The or a covariate variable to detect if there are any system- ¢ atic departures from zero in the residuals.
    [Show full text]
  • Measures of Fit for Logistic Regression Paul D
    Paper 1485-2014 Measures of Fit for Logistic Regression Paul D. Allison, Statistical Horizons LLC and the University of Pennsylvania ABSTRACT One of the most common questions about logistic regression is “How do I know if my model fits the data?” There are many approaches to answering this question, but they generally fall into two categories: measures of predictive power (like R-square) and goodness of fit tests (like the Pearson chi-square). This presentation looks first at R-square measures, arguing that the optional R-squares reported by PROC LOGISTIC might not be optimal. Measures proposed by McFadden and Tjur appear to be more attractive. As for goodness of fit, the popular Hosmer and Lemeshow test is shown to have some serious problems. Several alternatives are considered. INTRODUCTION One of the most frequent questions I get about logistic regression is “How can I tell if my model fits the data?” Often the questioner is expressing a genuine interest in knowing whether a model is a good model or a not-so-good model. But a more common motivation is to convince someone else--a boss, an editor, or an audience--that the model is OK. There are two very different approaches to answering this question. One is to get a statistic that measures how well you can predict the dependent variable based on the independent variables. I’ll refer to these kinds of statistics as measures of predictive power. Typically, they vary between 0 and 1, with 0 meaning no predictive power whatsoever and 1 meaning perfect predictions. Predictive power statistics available in PROC LOGISTIC include R-square, the area under the ROC curve, and several rank-order correlations.
    [Show full text]
  • Lecture 10: F-Tests, R2, and Other Distractions
    00:35 Friday 16th October, 2015 See updates and corrections at http://www.stat.cmu.edu/~cshalizi/mreg/ Lecture 10: F -Tests, R2, and Other Distractions 36-401, Section B, Fall 2015 1 October 2015 Contents 1 The F Test 1 1.1 F test of β1 = 0 vs. β1 6=0 .....................2 1.2 The Likelihood Ratio Test . .7 2 What the F Test Really Tests 11 2.1 The Essential Thing to Remember . 12 3 R2 16 3.1 Theoretical R2 ............................ 17 3.2 Distraction or Nuisance? . 17 4 The Correlation Coefficient 19 5 More on the Likelihood Ratio Test 20 6 Concluding Comment 21 7 Further Reading 22 1 The F Test The F distribution with a; b degrees of freedom is defined to be the distribution of the ratio 2 χa=a 2 χb =b 2 2 when χa and χb are independent. Since χ2 distributions arise from sums of Gaussians, F -distributed random variables tend to arise when we are dealing with ratios of sums of Gaussians. The outstanding examples of this are ratios of variances. 1 2 1.1 F test of β1 = 0 vs. β1 6= 0 1.1 F test of β1 = 0 vs. β1 6= 0 Let's consider testing the null hypothesis β1 = 0 against the alternative β1 6= 0, in the context of the Gaussian-noise simple linear regression model. That is, we won't question, in our mathematics, whether or not the assumptions of that model hold, we'll presume that they all do, and just ask how we can tell whether β1 = 0.
    [Show full text]
  • Goodness of Fit Tests for High-Dimensional Linear Models
    Goodness of fit tests for high-dimensional linear models Rajen D. Shah∗ Peter B¨uhlmann University of Cambridge ETH Z¨urich April 8, 2017 Abstract In this work we propose a framework for constructing goodness of fit tests in both low and high-dimensional linear models. We advocate applying regression methods to the scaled residuals following either an ordinary least squares or Lasso fit to the data, and using some proxy for prediction error as the final test statistic. We call this family Residual Prediction (RP) tests. We show that simulation can be used to obtain the critical values for such tests in the low-dimensional setting, and demonstrate using both theoretical results and extensive numerical studies that some form of the parametric bootstrap can do the same when the high- dimensional linear model is under consideration. We show that RP tests can be used to test for significance of groups or individual variables as special cases, and here they compare favourably with state of the art methods, but we also argue that they can be designed to test for as diverse model misspecifications as heteroscedasticity and nonlinearity. 1 Introduction High-dimensional data, where the number of variables may greatly exceed the number of obser- vations, has become increasingly more prevalent across a variety of disciplines. While such data pose many challenges to statisticians, we now have a variety of methods for fitting models to high- dimensional data, many of which are based on the Lasso [Tibshirani, 1996]; see B¨uhlmannand van de Geer [2011] for a review of some of the developments.
    [Show full text]