The Optimization of Training Loads in High Class Hurdlers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Weight Pentathlon Shall Be Included in the Team Events
EVAA TECHNICAL MANAGER WMA STADIA COMMITTEE MEMBER Dear athletes-Affiliates At the general assembly in san Sebastian there will be several point that will be raised regarding competition, as I am aware that many of the affiliates may not attend the assembly I would appreciate your feedback on some of the points raised in the following series of possible proposals. Even when you will have members attending it would be good for me to have some of your ideas as to these things, so that though I may be for or against them I have some feedback from my region, please mail me your comments and I will make a list for the meeting in August. Winston Thomas. [email protected] Possible Team medals in the Weight Pentathlon PROPOSAL The Weight Pentathlon shall be included in the team events, Team medal shall be awarded in the Weight Pentathlon. Awards will be for Women and men *M35 upwards in 5 year age groups Teams will consist of there scoring athlete Their total scores will be added to secure the final points. Athlete will be able to score in a lower age class only where they have no team in their own age group and all the implements are of the same specifications. For a trial period of 1 championships teams shall pay a €6.00 entry fee Teams will be free from this period as with other team events. *Note M35 should they be adopted by WMA/IAAF Ruling to be added in THE COMPETITION Field Events 12.(6) When team competitions are included in Weight pentathlon, there shall be three team awards on the basis that each Affiliate is entitled to count one team (best three to score) in five year age groups, and their results shall be computed on the points gained. -

TA0011 Adaptive Resource Cards
Use in conjunction with Eveque resource card No. 1 1A BALANCE TEST adaptations for all ability groups Description There are three suggested adaptations for the balance test and these adaptations can be taught as a progression enabling participants to learn the technique and find their own level of ability. The suggested adaptations are as follows the easiest being stage 1. Line Balance Test Stage 1 Twin Beam Balance Test Stage 2 Free Leg Balance Test Stage 3 Line Balance Test Procedure • Balance on a 50mm line on the floor. • Participants balance on one leg without holding the free leg. • Progression can be made to the holding of the free leg. • Give assistance to the participant where necessary. Equipment • Tape • Stopwatch Stage 1 Twin Beam Balance Test Procedure • Place two Balance Beams side by side and tape firmly together. • Participants balance on one leg without holding the free leg. • Progression can be made to the holding of the free leg. • Give assistance to the participant where necessary. Equipment • 2 x Balance Beams • Stopwatch • Tape Stage 2 Safety • Ensure that the balance beam is not able to slide on the floor. www.eveque.com © Eveque 2002. All material is used with kind permission of the International Funand Team Athletic Association. Use in conjunction with Eveque resource card No. 1 1A BALANCE TEST adaptations for all ability groups Free Leg Balance Procedure • As per the standard Balance Test, however, the participant does not need to hold their free leg. • Give assistance to the participant where necessary. Equipment • Balance Beam • Stopwatch • Balance Beam Mat (optional) Stage 3 Safety • Ensure that the balance beam is not able to slide on the floor. -

A Proposal to Change the Women's Hurdles Events by Sergio Guarda
VIEWPOINT Ptrgi -i^^ by l/V\F 8:2; 23-26. 1993 A proposal to change the 1 Introduction women's hurdles events The Sprint hurdles race, more or less, as we now know it. was 'invented' at Oxford University in 1864. The dislance was 12(1 by Sergio Guarda Etcheverry yards, with an approach and finish of 15 yards and a 10 yards spacing between 10 hurdles, 3 foot 6 inches in height. These measurements formed the basis for the event when it was included in the firsi modern Olympic Games, held at Athens in 1896. There, measurements became the metric equivalents. 1 Ul metres dislance. 10 hurdles 106.7cm in height and 9.14 metres apart, a dislance from starl line lo first hurdle of 13.72 metres and from lasl hurdle to finish of 14.02 meires. The first gold medal for the Olympic event was won by Thomas Curtis (USA) wilh a lime of 17 •V5 sec. From thai dale to the present, the rules of this event have noi been modified despite the progress made in lhe construc tion of the hurdles, in the quality of the track surface, in the quality of the shoes, in the selection of lhe athletes and in the spe cific training methodology and planning. Thc 400 metres Hurdles for men was incorporated in the programme for lhe Sergio Guarda Etcheverry is a professor 1900 Olympic Games, held in Paris. The of phvsical education al the Ufiivcisiiy of winner on this firsl occasion was Waller Santiago. Chile, andanteinberofihe Tewksbury (USA) with a time of 57.6 sec. -

HEEL and TOE ONLINE the Official Organ of the Victorian Race Walking
HEEL AND TOE ONLINE The official organ of the Victorian Race Walking Club 2019/2020 Number 40 Tuesday 30 June 2020 VRWC Preferred Supplier of Shoes, clothes and sporting accessories. Address: RUNNERS WORLD, 598 High Street, East Kew, Victoria (Melways 45 G4) Telephone: 03 9817 3503 Hours: Monday to Friday: 9:30am to 5:30pm Saturday: 9:00am to 3:00pm Website: http://www.runnersworld.com.au Facebook: http://www.facebook.com/pages/Runners-World/235649459888840 VRWC COMPETITION RESTARTS THIS SATURDAY Here is the big news we have all been waiting for. Our VRWC winter roadwalking season will commence on Saturday afternoon at Middle Park. Club Secretary Terry Swan advises the the club committee meet tonight (Tuesday) and has given the green light. There will be 3 Open races as follows VRWC Roadraces, Middle Park, Saturday 6th July 1:45pm 1km Roadwalk Open (no timelimit) 2.00pm 3km Roadwalk Open (no timelimit) 2.30pm 10km Roadwalk Open (timelimit 70 minutes) Each race will be capped at 20 walkers. Places will be allocated in order of entry. No exceptions can be made for late entries. $10 per race entry. Walkers can only walk in ONE race. Multiple race entries are not possible. Race entries close at 6PM Thursday. No entries will be allowed on the day. You can enter in one of two ways • Online entry via the VRWC web portal at http://vrwc.org.au/wp1/race-entries-2/race-entry-sat-04jul20/. We prefer payment by Credit Card or Paypal within the portal when you register. Ignore the fact that the portal says entries close at 10PM on Wednesday. -

Table of Contents
A Column By Len Johnson TABLE OF CONTENTS TOM KELLY................................................................................................5 A RELAY BIG SHOW ..................................................................................8 IS THIS THE COMMONWEALTH GAMES FINEST MOMENT? .................11 HALF A GLASS TO FILL ..........................................................................14 TOMMY A MAN FOR ALL SEASONS ........................................................17 NO LIGHTNING BOLT, JUST A WARM SURPRISE ................................. 20 A BEAUTIFUL SET OF NUMBERS ...........................................................23 CLASSIC DISTANCE CONTESTS FOR GLASGOW ...................................26 RISELEY FINALLY GETS HIS RECORD ...................................................29 TRIALS AND VERDICTS ..........................................................................32 KIRANI JAMES FIRST FOR GRENADA ....................................................35 DEEK STILL WEARS AN INDELIBLE STAMP ..........................................38 MICHAEL, ELOISE DO IT THEIR WAY .................................................... 40 20 SECONDS OF BOLT BEATS 20 MINUTES SUNSHINE ........................43 ROWE EQUAL TO DOUBELL, NOT DOUBELL’S EQUAL ..........................46 MOROCCO BOUND ..................................................................................49 ASBEL KIPROP ........................................................................................52 JENNY SIMPSON .....................................................................................55 -

Athletics Federations
QUALIFICATION SYSTEM – YOUTH OLYMPIC GAMES BUENOS AIRES 2018 INTERNATIONAL ASSOCIATION OF ATHLETICS FEDERATIONS Athletics A. EVENTS (38) Men’s Events (19) Women’s Events (19) Track Track 100m 100m 200m 200m 400m 400m 800m 800m 1500m* 1500m* 3000m* 3000m* 2000m Steeplechase* 2000m Steeplechase* 110m hurdles 100m hurdles 400m hurdles 400m hurdles 5’000m Race Walk 5’000m Race Walk Field Field High Jump High Jump Pole Vault Pole Vault Long Jump Long Jump Triple Jump Triple Jump Shot Put Shot Put Discus Throw Discus Throw Hammer Throw Hammer Throw Javelin Throw Javelin Throw Cross country* Cross country* Distance (4-6km) Distance (4-6km) Note*: All athletes entered in 1500m, 3000m and 2000m Steeple Chase to compete in Cross Country event. Original Version: ENGLISH 24 April 2018 Page 1/7 QUALIFICATION SYSTEM – YOUTH OLYMPIC GAMES BUENOS AIRES 2018 B. ATHLETES QUOTA 1. Total Quota for Athletics: Host Country Qualification Places Total Places Men 338 (includes Universality Places) 2 340 Women 338 (includes Universality Places) 2 340 Total 676 (includes Universality Places) 4 680 2. Maximum Number of Athletes per NOC: Quota per NOC Men 18* Women 18* Total 36* * One (1) athlete per event. Note: All athletes entered in 1500m, 3000m and 2000m Steeple Chase to compete in Cross Country event. 3. Type of Allocation of Quota Places: The quota place is allocated to the athlete(s) by name. C. ATHLETE ELIGIBILITY All athletes must comply with the provisions of the Olympic Charter currently in force, including but not limited to, Rule 41 (Nationality of Competitors). Only those athletes who have complied with the Olympic Charter may participate in the Youth Olympic Games. -

Performance Prediction in Track and Field
Western Michigan University ScholarWorks at WMU Master's Theses Graduate College 4-1992 Performance Prediction in Track and Field Ted James Dabbs Follow this and additional works at: https://scholarworks.wmich.edu/masters_theses Part of the Educational Assessment, Evaluation, and Research Commons, and the Health and Physical Education Commons Recommended Citation Dabbs, Ted James, "Performance Prediction in Track and Field" (1992). Master's Theses. 885. https://scholarworks.wmich.edu/masters_theses/885 This Masters Thesis-Open Access is brought to you for free and open access by the Graduate College at ScholarWorks at WMU. It has been accepted for inclusion in Master's Theses by an authorized administrator of ScholarWorks at WMU. For more information, please contact [email protected]. PERFORMANCE PREDICTION IN TRACK AND FIELD by Ted James Dabbs, Jr. A Thesis Submitted to the Faculty of The Graduate College in partial fulfillment of the requirements for the Degree of Master of Arts Department of Health, Physical Education and Recreation Western Michigan University Kalamazoo, Michigan April 1992 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. PERFORMANCE PREDICTION IN TRACK AND FIELD Ted James Dabbs, Jr., M. A. Western Michigan University, 1992 The study investigated the degree to which predicting performance in track and field relates to individual performances of track athletes. Predictive scores were determined for 26 male and 14 female athletes using prediction equations and test procedures developed by Henson, Turner, and Lacourse (1989a; 1989b). Predictive scores were compared to athletes' individual event point scores published in International Amateur A.thletic Federation (IAAF) men's and women's multi-event scoring tables ("Scoring Table for Men’s," 1962; "Scoring Table for Women's," 1971). -

2020 Tasmanian Combined Events Championships
Domain Athletics Centre - Site License Hy-Tek's MEET MANAGER 5:17 PM 13/01/2021 Page 1 2020 Tasmanian Combined Events Championships - 9/01/2021 Domain Athletic Centre, Hobart Results Women 10000 Metres Open ================================================================ Name Year Team Finals ================================================================ Finals 1 Vanessa Wilson 81 VIC 36:59.22 -- Meriem Daoui 99 NORTHERN SUBS DNF Heptathlon: #4 Women 200 Metres Under 18 Heptathlon ============================================================================ Name Year Team Finals Wind Points ============================================================================ 1 Isabella Davie 05 NEWSTEAD ATHLETICS 27.24 -2.0 692 2 Amy Wiggins 05 UNI OF TAS AC 28.37 -2.0 602 3 Bianca Anderson 05 NEWSTEAD ATHLETICS 29.60 -2.0 510 Heptathlon: #7 Women 800 Metres Under 18 Heptathlon ======================================================================= Name Year Team Finals Points ======================================================================= 1 Isabella Davie 05 NEWSTEAD ATHLETICS 2:31.90 669 2 Bianca Anderson 05 NEWSTEAD ATHLETICS 2:43.25 536 3 Amy Wiggins 05 UNI OF TAS AC 2:59.17 373 Heptathlon: #1 Women 100 Metres Hurdles (10 x .76m) Under 18 Heptathlon ============================================================================ Name Year Team Finals Wind Points ============================================================================ 1 Bianca Anderson 05 NEWSTEAD ATHLETICS 16.99 -0.7 598 2 Isabella Davie 05 NEWSTEAD ATHLETICS 17.21 -

Athletics at the Summer Olympic Games
Athletics at the Summer Olympic Games ATHLETICS AT THE SUMMER OLYMPIC GAMES Cristiana Lucretia POP 1 Abstract Athletics is the sport of the most natural human movements: running, walking, jumping and throwing and it accompanied the Olympic Games on its 120 years journey from their first beginning. Athletics hallmarked Olympics evolution with memorable moments, exceptional records, great personalities and the triumph of talent and fair play. The paper is a survey of relevant references and data related with athletic events in the summer Olympics program. Further I highlighted the important moments in athletics and modern Olympics history since the first edition until to the last held in Brazil. On this attempt I draw attention on the noting implications of political interference in the Olympics. A reverence has been made to those athletes either men and women representing with honor East European countries in major sporting events over the 20th century. Much have changed since 1896, not only in number of events, athletes, competition and prizes, but in philosophy, sport sciences, ethics and professional approach as well. Keywords: modern Olympic history, athletics, records, major sporting events, cold war JEL classification: I13, I23, I31 1. Introduction Baron Pierre de Coubertin launched the idea of reviving the Olympic Games at a time of great cultural effervescence. At the end of the XIX century, the focus was on Paris, the capital of the elite of art reformers from across Europe and other parts of the world. There was a revolution in art made up by an emblematic generation, inspired by the present that does not write, compose, or paint about other times, but makes history. -

The Influence Somatic Traits and Motor Fitness on Hurdle Race Results by Untrained Boys Aged 11-15
JOURNAL OF HUMAN KINETICS VOLUME 4, 2000 THE INFLUENCE SOMATIC TRAITS AND MOTOR FITNESS ON HURDLE RACE RESULTS BY UNTRAINED BOYS AGED 11-15 by JANUSZ ISKRA, WŁADYSŁAW MYNARSKI∗ The goal of this paper was aimed at evaluation of relationships between chosen efficiency variables and somatic constitution indexes with results of a hurdle race by untrained boys at the age of 11-15. Continuous measurements, carried out between 1994-1998, were preceded by pilot researches (1993-1994) aimed at determining the principles of the run (distance between hurdles, height of hurdles) for particular age categories. The research project included 42 boys, pupils of primary school No. 15 in Ruda Śląska. Two variations of hurdle race were adopted, with 3- and 4-stride rhythm between hurdles, along with battery of efficiency tests directed according to specificity of a discipline (20-30 m, 40-60 m, and 120-180 m runs, standing triple-jump, counter- movement jump, overhead medicine ball throw, forward bend and stepping onto a ladder). On the basis of the above mentioned tests, the following factors were calculated: - level of the technique of hurdle race, - co-ordination efficiency, - speed endurance, - flexibility of hip joint. For the analysis also used were variables of somatic constitution (body height and mass, length of lower limbs) to calculate Rohrer factor. Gathered data has been elaborated statistically to define normality of distribution of the variables under research, differences between results in successive years and differences between separated sub-groups (with a t-test, for dependent and independent variables). Interdependencies of results of a hurdle race with chosen motor fitness variables were evaluated by means of Pearson simple correlation coefficient. -

Kent Under 11 Sportshall Athletics Decathlon & County Trials
KCAA Kent under 11 Sportshall Athletics Decathlon & County Trials Sunday 15th January 2017 (School Years 5 & 6 only) Hosted and organised by Ashford Leisure Trust on behalf of the Kent County Sportshall Association. For the fifth year the trials will involve a sportshall athletics decathlon competition involving events for the regional fun in athletics event in February. The top performers from the decathlon competition and the KCAA championships on Sunday 11th December 2016 will be selected and invited to represent Kent at the South East Regional Fun in Athletics event to be held in February. Sportshall Athletics Decathlon Sunday 15th January 2017 10.00 - 1330 £5 entry fee (£13.00 including event t-shirt) At the Stour Centre, Ashford TN23 1ET Events (athletes will do all 10) Balance Test Chest Push Standing Long Jump Vertical Jump Speed Bounce 10 x 10m Shuttle Run Target Throw Soft Javelin Hi-Stepper Standing Triple Jump Following the decathlon events a series of 1 lap sprint and hurdle races will take place. Results from these races will be used to assist the selection of the final Kent Squad. Medals awarded to top three Boys and Girls Certificates for all Participants How to enter... Complete the form on page 2 and send along with entry fee (£5 or £13.00 with event t-shirt) to: Community Development Team, Ashford Leisure Trust, the Stour Centre, Station Approach, Ashford, Kent TN23 1ET Closing date for entries is Friday 6th January 2017 Note to parents - please be aware that this is not a club/team competition so we ask that a parent/responsible adult are present to supervise your child. -
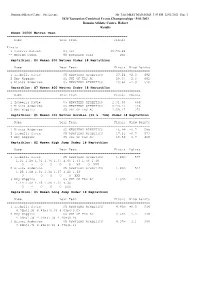
2020 Tasmanian Combined Events
Domain Athletics Centre - Site License Hy-Tek's MEET MANAGER 3:09 PM 12/01/2021 Page 1 2020 Tasmanian Combined Events Championships - 9/01/2021 Domain Athletic Centre, Hobart Results Women 10000 Metres Open ================================================================ Name Year Team Finals ================================================================ Finals 1 Vanessa Wilson 81 VIC 36:59.22 -- Meriem Daoui 99 NORTHERN SUBS DNF Heptathlon: #4 Women 200 Metres Under 18 Heptathlon ============================================================================ Name Year Team Finals Wind Points ============================================================================ 1 Isabella Davie 05 NEWSTEAD ATHLETICS 27.24 -2.0 692 2 Amy Wiggins 05 UNI OF TAS AC 28.37 -2.0 602 3 Bianca Anderson 05 NEWSTEAD ATHLETICS 29.60 -2.0 510 Heptathlon: #7 Women 800 Metres Under 18 Heptathlon ======================================================================= Name Year Team Finals Points ======================================================================= 1 Isabella Davie 05 NEWSTEAD ATHLETICS 2:31.90 669 2 Bianca Anderson 05 NEWSTEAD ATHLETICS 2:43.25 536 3 Amy Wiggins 05 UNI OF TAS AC 2:59.17 373 Heptathlon: #1 Women 100 Metres Hurdles (10 x .76m) Under 18 Heptathlon ============================================================================ Name Year Team Finals Wind Points ============================================================================ 1 Bianca Anderson 05 NEWSTEAD ATHLETICS 16.99 -0.7 598 2 Isabella Davie 05 NEWSTEAD ATHLETICS 17.21