First-Principles Study of Electronic Structure, Optical and Phonon
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Pressure-Amorphized State in Zirconium Tungstate: a Precursor to Decomposition
INSTITUTE OF PHYSICS PUBLISHING JOURNAL OF PHYSICS: CONDENSED MATTER J. Phys.: Condens. Matter 16 (2004) 1025–1031 PII: S0953-8984(04)67471-6 The pressure-amorphized state in zirconium tungstate: a precursor to decomposition Akhilesh K Arora1,3,VSSastry1,PChSahu1 and T A Mary2 1 Materials Science Division, Indira Gandhi Centre for Atomic Research, Kalpakkam 603 102, India 2 Department of Materials Science, California Institute of Technology, Pasadena, CA 91125, USA E-mail: [email protected] Received 12 August 2003, in final form 6 January 2004 Published 6 February 2004 Onlineatstacks.iop.org/JPhysCM/16/1025 (DOI: 10.1088/0953-8984/16/7/002) Abstract In contrast to widely accepted view that pressure-induced amorphization arises due to kinetic hindrance of equilibrium phase transitions, here we provide evidence that the metastable pressure-amorphized state in zirconium tungstate is aprecursor to decomposition of the compound into a mixture of simple oxides. This is from the volume collapse V across amorphization, which is obtained for the first time by measuring linear dimensions of irreversibly amorphized samples during their recovery to the original cubic phase upon isochronal annealing up to 1000 K. The anomalously large V of 25.7 ± 1.2% being the same as that expected for the decomposition indicates that this amorphous state is probably a precursor to kinetically hindered decomposition. A P–T diagram of the compound is also proposed. 1. Introduction At high pressure many materials exhibit structural phase transitions, while some become amorphous [1–7]. Although it is widely believedthat the phenomenon of pressure-induced amorphization (PIA) arises due to kinetic hindrance of equilibrium phase transitions, the structure of the equilibrium high-pressure phase, which the compound should have ideally evolved to, has remained speculative or unknown in most cases. -

Zirconium Tungstate
SAFETY DATA SHEET Issue Date 01-Apr-2020 Revision Date 01-Apr-2020 Version 1 1. IDENTIFICATION OF THE SUBSTANCE/PREPARATION AND OF THE COMPANY/UNDERTAKING Product identifier Product Name Zirconium Tungstate Other means of identification Product Code SAC032 Synonyms Zirconium Tungstate: Zirconium Tungsten Oxide, Tungsten Zirconium Oxide (Product #359) Recommended use of the chemical and restrictions on use Recommended Use Chemical intermediate. Uses advised against Details of the supplier of the safety data sheet Manufacturer Address ATI, 1000 Six PPG Place, Pittsburgh, PA 15222 USA Emergency telephone number Emergency Telephone Chemtrec: 1-800-424-9300 2. HAZARDS IDENTIFICATION Classification This material is considered hazardous by the 2012 OSHA Hazard Communication Standard (29 CFR 1910.1200) Skin corrosion/irritation Category 2 Serious eye damage/eye irritation Category 2 Specific target organ toxicity (single exposure) Category 3 Label elements Emergency Overview Warning Hazard statements Causes skin irritation Causes serious eye irritation May cause respiratory irritation Appearance Powder Physical state Solid Odor Odorless Precautionary Statements - Prevention Avoid breathing dust/fume Page 1 / 7 North America; English SAC032 Zirconium Tungstate Revision Date 01-Apr-2020 _____________________________________________________________________________________________ Wash hands thoroughly after handling Use only in well-ventilated areas Wear protective gloves/protective clothing/eye protection Precautionary Statements - Response IF ON SKIN: Wash with plenty of soap and water IF INHALED: Remove victim to fresh air and keep at rest in a position comfortable for breathing Call a POISON CENTER or doctor/physician if you feel unwell IF IN EYES: Rinse cautiously with water for several minutes. Remove contact lenses, if present and easy to do. -

22 Radiation Synthesis of Biopolymers for Removal Of
Radiation Synthesis of Biopolymers for Removal of Zirconium (IV) from Aqueous Solution Asmaa Sayed1, Yahya H.F. Al-Qudah2, Soad Yahya1, H. Kamal1 and El-Sayed A. Hegazy1 1Polymer Chemistry Department, National Center for Radiation Research and Technology, Atomic Energy authority Ahmed El-Zomor Street, El-Zohor District, Nasr City, P.O. Box 29, Cairo, Egypt 2Chemistry Department, Faculty of Science, Al-Balqa Applied University, P.O. Box 206; Al-Salt 19117 Jordan Abstract: This work explored the potential a cost-effective, simplistic and feasible method for commercial purposes to make sawdust polymeric films for zirconium Zr (IV) ions removal from aqueous medium. In this regard, cellulose acetate (CA) -co- Poly glycidyl methacrylate (PGMA) was prepared via radiation induced graft polymerization. The effect of sawdust content (SD) (wt%) on the properties of CA-co-PGMA biopolymer films was studied. The structural investigations and applicability of the prepared CA-co-PGMA/SD biopolymer films were carried out using XRD, SEM, FTIR, EDX and ICP. The introduction of more ionizable groups into the prepared biopolymer by NaOH-treatment regulated in improving its properties compared to untreated ones and these properties depend mainly on the number and form of the ionizable groups. Removal of zirconium (IV) from its aqueous medium was studied in batch mode experiments. The results of this study indicate that modification of CA-co-PGMA/SD biopolymer films shows great potential for simultaneous removal adsorptive of zirconium ions from its aqueous solution. Also, the prepared biopolymer has high efficiency for separation of Ti (IV) ions from its aqueous mixture with Zr (IV) ions. -

Multifunctional Polymer Composites Containing Inorganic Nanoparticles and Novel Low-Cost Carbonaceous Fillers Hongchao Wu Iowa State University
Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2014 Multifunctional polymer composites containing inorganic nanoparticles and novel low-cost carbonaceous fillers Hongchao Wu Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Mechanics of Materials Commons Recommended Citation Wu, Hongchao, "Multifunctional polymer composites containing inorganic nanoparticles and novel low-cost carbonaceous fillers" (2014). Graduate Theses and Dissertations. 13708. https://lib.dr.iastate.edu/etd/13708 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Multifunctional polymer composites containing inorganic nanoparticles and novel low- cost carbonaceous fillers by Hongchao Wu A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Materials Science and Engineering Program of Study Committee: Michael R. Kessler, Major Professor Xiaoli Tan Nicola Bowler Gap-Yong Kim Samy Madbouly Iowa State University Ames, Iowa 2014 Copyright © Hongchao Wu, 2014. All rights reserved. ii TABLE OF CONTENT LIST OF FIGURES.................................................................................................................. -

Thesis Outline
A Thesis Entitled Autohydration of Nanosized Cubic Zirconium Tungstate by Nathan A. Banek Submitted to the Graduate Faculty as partial fulfillment of the requirements for the Master of Science in Chemistry ___________________________________ Dr. Cora Lind, Committee Chair ___________________________________ Dr. Jared Anderson, Committee Member ___________________________________ Dr. Jon Kirchhoff, Committee Member ___________________________________ Dr. Patricia Komuniecki Dean of College of Graduate Studies The University of Toledo August 2011 An Abstract of Autohydration of Nanosized Cubic Zirconium Tungstate by Nathan A. Banek Submitted in partial fulfillment of the requirements for The Master of Science in Chemistry The University of Toledo August 2011 In recent years, negative thermal expansion (NTE) materials have become of increasing interest. These materials contract upon heating, and have potential for achieving better control of thermal expansion in composite materials. By using an NTE compound as a filler material into these composites, it is possible to offset the positive thermal expansion of other components in the composite. As a result, these NTE materials can find use in a wide range of applications such as optics, polymers, electronics, tooth fillings and any other area where exact positioning of parts over a wide range of temperatures is crucial. One of the most popular NTE materials is cubic ZrW2O8. Thermodynamically stable zirconium tungstate was first synthesized in the 1950’s through traditional solid state methods. It was only recent that the metastable phases could be achieved through low temperature methods, that involves conversion of a precursor material ZrW2O7(OH)2·2H2O to cubic ZrW2O8. Through hydrothermal synthesis, previous work on ZrW2O7(OH)2·2H2O showed exceptional particle and morphology control with use of iii alcohols/HCl, which is desirable for optimal composite integration. -

Structural, Fatigue Behavior, and Mechanical Properties of Zirconium Tungstate-Reinforced Casted A356 Aluminum Alloy
metals Article Structural, Fatigue Behavior, and Mechanical Properties of Zirconium Tungstate-Reinforced Casted A356 Aluminum Alloy Muhammad Raza 1, Hussein Alrobei 2,* , Rizwan Ahmed Malik 1, Azhar Hussain 1, Meshal Alzaid 3 , Mohsin Saleem 4 and Mian Imran 5 1 Department of Metallurgy and Materials Engineering, University of Engineering and Technology, Taxila 47050, Pakistan; razajaff[email protected] (M.R.); [email protected] (R.A.M.); [email protected] (A.H.) 2 Department of Mechanical Engineering, College of Engineering, Prince Sattam bin Abdul aziz University, AlKharj 11942, Saudi Arabia 3 Physics Department, College of Science, Jouf University, Al-Jouf, Sakaka 2014, Saudi Arabia; [email protected] 4 School of Chemical and Materials Engineering, National University of Sciences and Technology (NUST), Islamabad 44000, Pakistan; [email protected] 5 Department of Mechanical Engineering, Institute of Space Technology, Islamabad 44000, Pakistan; [email protected] * Correspondence: [email protected]; Tel.: +966-11-588-8272 Received: 28 September 2020; Accepted: 2 November 2020; Published: 9 November 2020 Abstract: The aim of this study is to investigate the structure–property relationship of the zirconium tungstate-reinforced casted A356 aluminum alloy. The reinforcement ceramic used was zirconium tungstate of the negative thermal coefficient type, which assists in the weldment of crack growth and enhances the fatigue life. The specimens used in this study were casted by stir casting method and prepared according to Compact Tension standard E-399, and microstructural, fatigue behavior, and mechanical properties were investigated systematically. Microstructural analysis showed reduction in porosity by the addition of ZrW2O8 particles. Fatigue results depict the increase in the fatigue life of aluminum reinforced ceramic as compared to the casted base aluminum alloy. -

Material Safety Data Sheet
LTS Research Laboratories, Inc. Safety Data Sheet Zirconium Tungsten Oxide ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– 1. Product and Company Identification ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Trade Name: Zirconium Tungsten Oxide Chemical Formula: Zr(WO4)2 Recommended Use: Scientific research and development Manufacturer/Supplier: LTS Research Laboratories, Inc. Street: 37 Ramland Road City: Orangeburg State: New York Zip Code: 10962 Country: USA Tel #: 855-587-2436 / 855-lts-chem 24-Hour Emergency Contact: 800-424-9300 (US & Canada) +1-703-527-3887 (International) ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– 2. Hazards Identification ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Signal Word: None Hazard Statements: None Precautionary Statements: None HMIS Health Ratings (0-4): Health: 1 Flammability: 0 Physical: 1 ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– 3. Composition ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Chemical Family: Ceramic Additional Names: Zirconium Tungstate Zirconium Tungstate (Zr(WO4)2): Percentage: 0-100 wt% CAS #: 16853-74-0 EC #: 240-876-3 ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– 4. First Aid Procedures ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– -

The Influence of the Modification of Zirconium Tungstate with Eu(III) on the Α → Β Phase Transition Temperature and Optical Band Gap
Bulgarian Chemical Communications, Volume 50, Special Issue F (pp. 143–149) 2018 The influence of the modification of zirconium tungstate with Eu(III) on the α → β phase transition temperature and optical band gap E. D. Encheva, M. K. Nedyalkov, M. P. Tsvetkov, M. M. Milanova* University of Sofia “St. Kl. Ohridski”, Faculty of Chemistry and Pharmacy, Department of Inorganic Chemistry, Laboratory of rare and rare earth elements, 1 J. Bourchier Blvd., 1164 Sofia, Bulgaria Received October 22, 2018; Accepted December 01, 2018 The hydrothermal method was used to obtain pure and Eu(III)-modified ZrW2O8. Tungstates modified with 1, 2, and 5 mol% Eu(III) were synthesized in order to investigate the influence of Eu(III) doping on the properties of zirconium tungstate. The samples obtained were phase homogeneous as shown by XRD. High temperature XRD was used to follow the temperature of the alpha-beta phase transition. It was observed that the higher the content of Eu(III), the higher the temperature of the transition. The unit cell parameters decrease both with the Eu(III) content and the temperature increasing. Тhe values of the thermal expansion coefficients obtained decreased with increasing Eu(III) for both the alpha and beta phases of ZrW2O8. Doping with increasing amounts of Eu(III) increased the energy of the optical band gap as well. Keywords: zirconium tungstate, Eu(III) modification, XRD, phase transition, band gap energy. INTRODUCTION tion. The temperature of the transition is not well defined and in the literature the values for it vary in In the recent years the modification of tung- the range between 157 °C and 175 °C [10]. -

Solid Acid Catalysts Based on Supported Tungsten Oxides
Topics in Catalysis 6 (1998) 87±99 87 Solid acid catalysts based on supported tungsten oxides a b a, David G. Barton ,StuartL.Soled and Enrique Iglesia ∗ a Department of Chemical Engineering, University of California at Berkeley, Berkeley, CA 94720, USA E-mail: [email protected] b Corporate Research Laboratory, Exxon Research and Engineering, Route 22 East, Annandale, NJ 08801, USA Supported WOx clusters are active and stable catalysts for isomerization, dehydration, and cracking reactions. Brùnsted acid sites 6+ 6+ form on WOx clusters when a lower valent element replaces W or when W centers reduce slightly during catalytic reactions. WOx clusters of intermediate size provide the balance between reducibility and accessibility required to maximize the number of surface H+ species in WOx±ZrO2, zirconium tungstate, and oxygen-modi®ed WC catalysts. H2 is involved in the generation and maintenance of Brùnsted acid sites during catalytic reactions on WOx clusters. Keywords: tungsten oxides, solid acids, acid-catalyzed reactions 1. Introduction (WOx±ZrO2) by impregnation with a solution of tungstate anions and subsequent oxidation treatments at high tem- Many research groups continue to explore the catalytic peratures (873±1173 K) show strong acidity. Hino and properties of oxide-based strong solid acids in an attempt to Arata suggested, based on color changes of Hammett in- eliminate environmental concerns caused by the use, regen- dicators (H0 14:52), that acid sites stronger than 100% 6 − eration, and disposal of liquid acids and halide-containing sulfuric acid may exist [4]; however, the use of this tech- solids [1,2]. The challenge of obtaining acid site strength nique to measure acid strength of solids is often unreli- and density comparable to those in sulfuric acid, halides, able [5]. -

Use of Zirconium Tungstate in Acid Catalysis
Indian Journal of Chemistry Vol. 31 A, October 1992, pp. 803-805 Use of zirconium tungstate in acid catalysis: The ion exchange property of a-zirconium Some esterification reactions phosphate, Zr(HP04hHzO has been examined in detail5-7 and in the hydrogen form shown to be an Pramod Patel, Anjali Shivanekar & Uma Chudasama· acidic catalyst8,9. It has been shown by us earlier, Department of Chemistry, Faculty of Science, M S University of the potential use of zirconium molytxlate as a Baroda, Baroda 390 002 Bronsted acid catalystlO• The synthesis and ion ex• change properties of zirconium tungstate has been Received 9 December 1991; revised 10 March 1992; accepted studied earlierll-13• So far no work has been done 1 May 1992 to examine the catalytic properties of these com• pounds. The present work consists of synthesis, Amorphous zirconium tungstate, an inorganic cation characterisation and study of catalytic behaviour exchanger has been prepared. The protons of the hy• (Bronsted acid catalyst) of amorphous zirconium droxyl groups are the active sites. Such a material indi• tungstate (ZW) using esterification as a mOdel cates good potential for application in Bronsted cataly• reaction. sis. Esterification has been studied as a model reaction wherein ethyl acetate has been synthesized. The variation of Experimental several parameters has established the use of zirconium tungstate as a Bronsted acid catalyst. Preparation of the catalyst Zirconium tungstate was prepared by adding sodium· tungstate to an aqueous solution of zirco• Acid salts of tetravalent metals are usually ob• nium oxychloride till complete precipitation. The tained as amorphous materials I, but of late they gel was digested at room temperature for several have been obtained as crystalline compoundsz. -
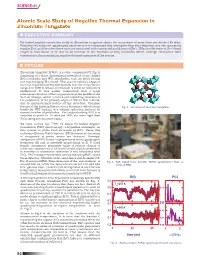
Atomic Scale Study of Negative Thermal Expansion in Zirconium Tungstate N EXECUTIVE SUMMARY
SCIENCE-41 Atomic Scale Study of Negative Thermal Expansion in Zirconium Tungstate n EXECUTIVE SUMMARY Perturbed angular correlation study in Zirconium tungstate shows the occurrence of more than one distinct Zr sites. Based on the values of quadrupole parameters it is interpreted that among the four sites observed, one site represents regular ZrO6 and the other three sites are associated with contracted and distorted ZrO6 . Effective decrease in Zr-O bond length is understood to be due to an increase in the fractions of ZrO6 octahedra which undergo contraction with temperature, thus explaining negative thermal expansion of the system. n OUTLINE Zirconium tungstate ZrW28 O is a cubic compound (Cf. Fig.1) consisting of a three dimensional network of corner linked ZrO6 octahedra and WO4 tetrahedra, with the latter having one non-bridging W-O bond. This system exhibits negative (A) thermal expansion (NTE) isotropically over the temperature range 4 to 1000 K, whose mechanism is yet to be completely understood. It was earlier understood that a large transverse vibration of the oxygen atom in the middle of the W-O-Zr linkage, which requires corresponding rotations of the polyhedra, is the primary origin of NTE in this material due to unconstrained feature of the structure. Common feature of the existing literature is a dominant role of strong Fig. 1 : Structure of zirconium tungstate. bonds for NTE leading to a volume reduction induced by inward rotation of polyhedra. For understanding NTE it is essential to probe at Zr sites (as WO4 are more rigid than ZrO6 ) using any local technique. -

Physical and Thermal Properties of Zirconium Tungstate Nanoparticles with Different Morphologies from Hydrothermal Synthesis Hongchao Wu Iowa State University
Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2012 Physical and Thermal Properties of Zirconium Tungstate Nanoparticles with Different Morphologies from Hydrothermal Synthesis Hongchao Wu Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Engineering Commons Recommended Citation Wu, Hongchao, "Physical and Thermal Properties of Zirconium Tungstate Nanoparticles with Different Morphologies from Hydrothermal Synthesis" (2012). Graduate Theses and Dissertations. 12525. https://lib.dr.iastate.edu/etd/12525 This Thesis is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Physical and thermal properties of zirconium tungstate nanoparticles with different morphologies from hydrothermal synthesis By: Hongchao Wu A thesis submitted to the graduate faculty in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Major: Materials Science and Engineering Program of Study Committee: Michael R. Kessler - Major Professor Mufit Akinc David Grewell Iowa State University Ames, Iowa 2012 Copyright © Hongchao Wu, 2012. All rights reserved. ii Table of Contents Acknowledgements ...............................................................................................................................