DOCSLIB.ORG

Fractional Versions of the Fundamental Theorem of Calculus

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fractional Versions of the Fundamental Theorem of Calculus Applied Mathematics, 2013, 4, 23-33 http://dx.doi.org/10.4236/am.2013.47A006 Published Online July 2013 (http://www.scirp.org/journal/am) Fractional Versions of the Fundamental Theorem of Calculus Eliana Contharteze Grigoletto, Edmundo Capelas de Oliveira Department of Applied Mathematics, University of Campinas, Campinas, Brazil Email: [email protected], [email protected] Received April 27, 2013; revised May 27, 2013; accepted June 7, 2013 Copyright © 2013 Eliana Contharteze Grigoletto, Edmundo Capelas de Oliveira. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT The concept of fractional integral in the Riemann-Liouville, Liouville, Weyl and Riesz sense is presented. Some prop- erties involving the particular Riemann-Liouville integral are mentioned. By means of this concept we present the frac- tional derivatives, specifically, the Riemann-Liouville, Liouville, Caputo, Weyl and Riesz versions are discussed. The so-called fundamental theorem of fractional calculus is presented and discussed in all these different versions. Keywords: Fractional Integral; Fractional Derivative; Riemann-Liouville Derivative; Liouville Derivative; Caputo Derivative; Weyl Derivative and Riesz Derivative 1. Introduction much research on its applications as there is on the cal- culus of integer order. Several applications in all areas of Fractional calculus, a popular name used to denote the knowledgement are collected, presented and discussed in calculus of non integer order, is as old as the calculus of different books as follow [7-12]. integer order as created independently by Newton and The main objective of this paper is to explain what is Leibniz. In contrast with the calculus of integer order, meant by calculus of non integer order and collect any fractional calculus has been granted a specific area of different versions of the fractional derivatives associated mathematics only in 1974, after the first international with a particular fractional integral. Specifically, we re- congress dedicated exclusively to it. Before this congress there were only sporadic independent papers, without a cover the concepts of fractional integral and fractional consolidated line [1,2]. derivative in different versions and present a new version During the 1980s fractional calculus attracted re- of the so-called fundamental theorem of fractional cal- searchers and explicit applications began to appear in culus (FTFC), which is interpreted as a generalization of several fields. We mention the doctoral thesis, published the classical fundamental theorem of calculus. We men- as an article [3], which seems to be the first one in the tion three recent works where FTFC is discussed, Tara- subject and the classical book by Miller and Ross [1], sov’s book [12], a paper by Tarasov [13] and a paper by where one can see a timeline from 1645 to 1974. After Dannon [14] in which a particular case of the parameter the decade of 1990, completely consolidated, there ap- associated with the derivative is presented. The paper is peared some specific journals and several textbooks were written as follows: in section two, we first review the published. These facts lent a great visibility to the subject concept of fractional integral in the Riemann-Liouville and it gained prestige around the world. An interesting sense, which can be interpreted as a generalization of the timeline from 1645 to 2010 is presented in references integral of integer order and in the Liouville sense, which [4-6]. We recall here that an important advantage of us- is a particular case of the Riemann-Liouville one. We ing fractional differential equations in applications is review also the concept of fractional integral in the Weyl their non-local property. The use of fractional calculus is sense and in the Riesz sense. Section two present also the more realistic and this is one reason why fractional cal- concepts of derivative as proposed by Riemann-Liouville, culus has become more popular. Liouville, Caputo, Weyl and Riesz, showing the real im- Nowadays, fractional calculus can be considered a portance and applications. Some properties are also pre- frontier area in mathematics in the sense that there is as sented, among which one associated with the semigroup Copyright © 2013 SciRes. AM 24 E. C. GRIGOLETTO, E. C. DE OLIVEIRA property. Our main result appears in section three, in and if Re 0 or 0 , then which we present and demonstrate the many faces of the IIaaIa an d IIbb I b . FTFC, in all different versions and which are interpreted (Riemann-Liouville integrals) Let1 f xaL,1 b , as a generalization of the fundamental theorem of calcu- with ab . The fractional integrals of Rie- lus. Applications are presented in section four. mann-Liouville of order with Re 0 , on the left and on the right, are defined respectively by 2. Fractional Calculus 1 x f The integral and derivatives of non integer order have I:a f xx 1 d , with a , a several applications and are used to solve problems in x different fields of knowledge, specifically, involving a and fractional differential equation with boundary value con- 1 b f I: f xx d , with b . ditions and/or initial conditions [7,9,11,12]. They can be b 1 x x seen as generalizations of the integral and derivatives of 00 integer order. On the other hand, we mention two papers, If 0 , we have IIab :=I, where I is the iden- by Heymans & Podlubny [15] and Podlubny [16] that tity operator. provide an interesting geometric interpretation, and dis- cuss applications of fractional calculus, with integral and 2.2. Fractional Derivative of Riemann-Liouville derivatives of non integer order. Also, we mention a re- After we introduce the fractional integral in the Rie- cent paper in which the authors discuss a fractional dif- mann-Liouville sense, we define the fractional derivative ferential equation with integral boundary value condi- of Riemann-Liouville, which is the most used by mathe- tions [17]. We remember that, there are several ways to maticians, particularly, into the problems in which the introduce the concepts of fractional integral and frac- initial conditions are not involved. tional derivatives, which are not necessarily coincident (Riemann-Liouville derivative) Let , with with each other [18]. The so-called Grünwald-Letnikov Re 0 and n Re 1 , where denotes derivative, which will be not discussed in this paper, is the integer part of , the fractional derivatives in the convenient and useful to affront problems involving a Riemann-Liouville sense, on the left and on the right, are numerical treatment [19]. defined by In this section, the concept of fractional integral in the n Riemann-Liouville, Liouville, Weyl and Riesz sense is d n D:Iaaf xf n x (1) presented. Some properties involving the particular Rie- dx mann-Liouville integral are mentioned. By means of this and concept we present the fractional derivatives, specifically, n n d n the Riemann-Liouville, Liouville, Caputo, Weyl and Ri- D:1Ibbf xf n x, (2) dx esz versions are discussed. respectively. Note that the derivatives in Equations (1) and (2) exist 2.1. Fractional Integral of Riemann-Liouville for2 f xa ACn ,b . The fractional integral of Riemann-Liouville is an inte- If, in particular, n , then gral that generalizes the concept of integral in the classi- n n cal sense, and which can be obtained as a generalization Da f xfx of the Cauchy-Riemann integral. As we have already said, and before we define the fractional integral Riemann-Liou- D=(1)nnf xf ()n()x. ville. b Definition 1 (Spaces IL and IL The ap ap 2.3. Fractional Integral and Derivative in the spaces ILap and ILap are defined, for Liouville Sense Re 0 and p 1, by An interesting particular case of the fractional integral of p IL:apf xfx : I a gxgx , L, ab Riemann-Liouville and the corresponding fractional de- rivative, is the so-called Liouville fractional integral and and 1 p b 1 p p p IL:apf xfx : I a hxhx , L, ab fx Lab ,if fx d x ,for1 p . a respectively. 2Space of complex functions f x whose derivatives up to order Property 2.1 (Semigroup) If Re 0 or 0 n 1 are absolutely continuous on ab, . Copyright © 2013 SciRes. AM E. C. GRIGOLETTO, E. C. DE OLIVEIRA 25 the Liouville fractional derivative. This case is obtained W inx Iefx cinn by substitution a and b in the expres- n sions associated with the fractional integral in the Rie- n0 and mann-Liouville sense. inx (Liouville integral and derivative) The fractional inte- Wefx cinn , n grals in the Liouville sense on the real axis, on the left n0 and on the right, for x and Re 0 , are defined respectively, with and Re 0 . by In the particular case 0 1, if fxL0,21 , 1 x f W Ifx d (3) then IIf xfx and WDx f xf x , 1 x where I and D are defined in Equations (3) and (5), and respectively. If we define the Fourier series of f x in 1 f the form I fx d , (4) x 1 x 1 2 f x ceinx , with c einx fxx d , nn0 n 2 respectively. n0 The corresponding fractional derivatives in the Liou- then we obtain for 01 , in the same way, the frac- ville sense are given by tional integral in the Weyl sense on the right and the n fractional derivative on the right, defined by d n D:If xf n x (5) dx W IIf xfx and n and n d n D:1Ifx n fx, (6) x WDf xfx . dx respectively.
Load more

Recommended publications
  • Arxiv:1507.07356V2 [Math.AP]
    TEN EQUIVALENT DEFINITIONS OF THE FRACTIONAL LAPLACE OPERATOR MATEUSZ KWAŚNICKI Abstract. This article discusses several definitions of the fractional Laplace operator ( ∆)α/2 (α (0, 2)) in Rd (d 1), also known as the Riesz fractional derivative − ∈ ≥ operator, as an operator on Lebesgue spaces L p (p [1, )), on the space C0 of ∈ ∞ continuous functions vanishing at infinity and on the space Cbu of bounded uniformly continuous functions. Among these definitions are ones involving singular integrals, semigroups of operators, Bochner’s subordination and harmonic extensions. We collect and extend known results in order to prove that all these definitions agree: on each of the function spaces considered, the corresponding operators have common domain and they coincide on that common domain. 1. Introduction We consider the fractional Laplace operator L = ( ∆)α/2 in Rd, with α (0, 2) and d 1, 2, ... Numerous definitions of L can be found− in− literature: as a Fourier∈ multiplier with∈{ symbol} ξ α, as a fractional power in the sense of Bochner or Balakrishnan, as the inverse of the−| Riesz| potential operator, as a singular integral operator, as an operator associated to an appropriate Dirichlet form, as an infinitesimal generator of an appropriate semigroup of contractions, or as the Dirichlet-to-Neumann operator for an appropriate harmonic extension problem. Equivalence of these definitions for sufficiently smooth functions is well-known and easy. The purpose of this article is to prove that, whenever meaningful, all these definitions are equivalent in the Lebesgue space L p for p [1, ), ∈ ∞ in the space C0 of continuous functions vanishing at infinity, and in the space Cbu of bounded uniformly continuous functions.
    [Show full text]
  • Riesz Potentials and Liouville Operators on Fractals
    RIESZ POTENTIALS AND LIOUVILLE OPERATORS ON FRACTALS by M. Zähle Mathematical Institute, University of Jena, D-07740 Jena, Germany E-mail: [email protected] Abstract An analogue to the theory of Riesz potentials and Liouville operators in Rn for arbitrary fractal d-sets is developed. Corresponding function spaces agree with traces of euclidean Besov spaces on fractals. By means of associated quadratic forms we construct strongly continuous semigroups with Liouville operators as infinitesimal generator. The case of Dirichlet forms is discussed separately. As an example of related pseudodifferential equations the fractional heat-type equation is solved. Mathematics Subject Classification. Primary 28A80, Secondary 47B07, 35P20 Keywords. fractal d-set, Riesz potential, pseudodifferential operator, fractal Besov space, Dirichlet form 0 Introduction In [17] the Riesz potential of order s of a fractal d-measure µ in Rn with compact support Γ is defined as Z s −(d−s) Iµf(x) := const |x − y| f(y)µ(dy) , f ∈ L2(µ) , where 0 < s < d < n . (Examples for the measure µ are the Haus- dorff measures Hd on arbitrary self-similar sets Γ of dimension d.) Such potentials have a long tradition for the case, where µ is replaced by the Lebesgue measure. For more general µ only a view properties are known. Some references may be found in [17]. We also refer to the fundamental paper [2]. In connection with harmonic analysis and stochastic processes on fractals these potentials appear in a new light. The aim of the present paper is to continue this study in order to get a deeper insight into the interplay between geometry of and analysis on fractal sets and the corresponding properties of the embedding euclidean space.
    [Show full text]
  • Fourier Multipliers and Dirac Operators
    Fourier Multipliers and Dirac Operators Craig A. Nolder and Guanghong Wang Abstract. We use Fourier multipliers of the Dirac operator and Cauchy transform to obtain composition theorems and integral representations. In particular we calculate the multiplier of the Π-operator. This opera- tor is the hypercomplex version of the Beurling Ahlfors transform in the plane. The hypercomplex Beuling Ahlfors transform is a direct general- ization of the Beurling Ahlfors transform and reduces to this operator in the plane. We give an integral representation for iterations of the hyper- complex Beurling Ahlfors transform and we present here a bound for the Lp-norm. Such Lp-bounds are essential for applications of the Beurling Ahlfors transformation in the plane. The upper bound presented here is m(p∗ −1) where m is the dimension of the Euclidean space on which the functions are defined, 1 < p < 1 and p∗ = max(p; p=(p − 1)): We use recent estimates on second order Riesz transforms to obtain this result. Using the Fourier multiplier of the Π operator we express this operator as a hypercomplex linear combination of second order Riesz transforms. Keywords. Fourier multipliers, Clifford analysis, Dirac operators, Π op- erator, Beurling Ahlfors transform, Lp-estimates. msc : 47F, 47G, 30G 1. Introduction We determine the Fourier multipliers of the hypercomplex Cauchy transform T and the Vekua Π-operator over Rn+1: Various relations between these op- erators, and the Dirac and Laplacian operator, are easily obtained using these 1 n+1 multipliers. Theorem 3.2 is a convolution identity on C0 (R ) involving the iterated Cauchy kernel and Dirac operator.
    [Show full text]
  • Definition of Riemann Integrals
    The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) Let [a; b] be a given interval. By a partition P of [a; b] we mean a finite set of points x0; x1;:::; xn where a = x0 ≤ x1 ≤ · · · ≤ xn−1 ≤ xn = b We write ∆xi = xi − xi−1 for i = 1;::: n. The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) Now suppose f is a bounded real function defined on [a; b]. Corresponding to each partition P of [a; b] we put Mi = sup f (x)(xi−1 ≤ x ≤ xi ) mi = inf f (x)(xi−1 ≤ x ≤ xi ) k X U(P; f ) = Mi ∆xi i=1 k X L(P; f ) = mi ∆xi i=1 The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) We put Z b fdx = inf U(P; f ) a and we call this the upper Riemann integral of f . We also put Z b fdx = sup L(P; f ) a and we call this the lower Riemann integral of f . The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) If the upper and lower Riemann integrals are equal then we say f is Riemann-integrable on [a; b] and we write f 2 R. We denote the common value, which we call the Riemann integral of f on [a; b] as Z b Z b fdx or f (x)dx a a The Definition and Existence of the Integral Left and Right Riemann Integrals If f is bounded then there exists two numbers m and M such that m ≤ f (x) ≤ M if (a ≤ x ≤ b) Hence for every partition P we have m(b − a) ≤ L(P; f ) ≤ U(P; f ) ≤ M(b − a) and so L(P; f ) and U(P; f ) both form bounded sets (as P ranges over partitions).
    [Show full text]
  • Generalizations of the Riemann Integral: an Investigation of the Henstock Integral
    Generalizations of the Riemann Integral: An Investigation of the Henstock Integral Jonathan Wells May 15, 2011 Abstract The Henstock integral, a generalization of the Riemann integral that makes use of the δ-fine tagged partition, is studied. We first consider Lebesgue’s Criterion for Riemann Integrability, which states that a func- tion is Riemann integrable if and only if it is bounded and continuous almost everywhere, before investigating several theoretical shortcomings of the Riemann integral. Despite the inverse relationship between integra- tion and differentiation given by the Fundamental Theorem of Calculus, we find that not every derivative is Riemann integrable. We also find that the strong condition of uniform convergence must be applied to guarantee that the limit of a sequence of Riemann integrable functions remains in- tegrable. However, by slightly altering the way that tagged partitions are formed, we are able to construct a definition for the integral that allows for the integration of a much wider class of functions. We investigate sev- eral properties of this generalized Riemann integral. We also demonstrate that every derivative is Henstock integrable, and that the much looser requirements of the Monotone Convergence Theorem guarantee that the limit of a sequence of Henstock integrable functions is integrable. This paper is written without the use of Lebesgue measure theory. Acknowledgements I would like to thank Professor Patrick Keef and Professor Russell Gordon for their advice and guidance through this project. I would also like to acknowledge Kathryn Barich and Kailey Bolles for their assistance in the editing process. Introduction As the workhorse of modern analysis, the integral is without question one of the most familiar pieces of the calculus sequence.
    [Show full text]
  • Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration Over a Polygonal Element Sulaiman Abo Diab
    Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration over a Polygonal Element Sulaiman Abo Diab To cite this version: Sulaiman Abo Diab. Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration over a Polygonal Element. 2019. hal-02306578v1 HAL Id: hal-02306578 https://hal.archives-ouvertes.fr/hal-02306578v1 Preprint submitted on 6 Oct 2019 (v1), last revised 5 Nov 2019 (v2) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration over a Polygonal Element Sulaiman Abo Diab Faculty of Civil Engineering, Tishreen University, Lattakia, Syria [email protected] Abstracts: In this paper, the Riemann integral and the fundamental of calculus will be used to perform double integrals on polygonal domain surrounded by closed curves. In this context, the double integral with two variables over the domain is transformed into sequences of single integrals with one variable of its primitive. The sequence is arranged anti clockwise starting from the minimum value of the variable of integration. Finally, the integration over the closed curve of the domain is performed using only one variable.
    [Show full text]
  • Lecture Notes: Harmonic Analysis
    Lecture notes: harmonic analysis Russell Brown Department of mathematics University of Kentucky Lexington, KY 40506-0027 August 14, 2009 ii Contents Preface vii 1 The Fourier transform on L1 1 1.1 Definition and symmetry properties . 1 1.2 The Fourier inversion theorem . 9 2 Tempered distributions 11 2.1 Test functions . 11 2.2 Tempered distributions . 15 2.3 Operations on tempered distributions . 17 2.4 The Fourier transform . 20 2.5 More distributions . 22 3 The Fourier transform on L2. 25 3.1 Plancherel's theorem . 25 3.2 Multiplier operators . 27 3.3 Sobolev spaces . 28 4 Interpolation of operators 31 4.1 The Riesz-Thorin theorem . 31 4.2 Interpolation for analytic families of operators . 36 4.3 Real methods . 37 5 The Hardy-Littlewood maximal function 41 5.1 The Lp-inequalities . 41 5.2 Differentiation theorems . 45 iii iv CONTENTS 6 Singular integrals 49 6.1 Calder´on-Zygmund kernels . 49 6.2 Some multiplier operators . 55 7 Littlewood-Paley theory 61 7.1 A square function that characterizes Lp ................... 61 7.2 Variations . 63 8 Fractional integration 65 8.1 The Hardy-Littlewood-Sobolev theorem . 66 8.2 A Sobolev inequality . 72 9 Singular multipliers 77 9.1 Estimates for an operator with a singular symbol . 77 9.2 A trace theorem. 87 10 The Dirichlet problem for elliptic equations. 91 10.1 Domains in Rn ................................ 91 10.2 The weak Dirichlet problem . 99 11 Inverse Problems: Boundary identifiability 103 11.1 The Dirichlet to Neumann map . 103 11.2 Identifiability . 107 12 Inverse problem: Global uniqueness 117 12.1 A Schr¨odingerequation .
    [Show full text]
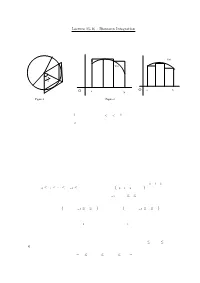
  • Lecture 15-16 : Riemann Integration Integration Is Concerned with the Problem of finding the Area of a Region Under a Curve
    1 Lecture 15-16 : Riemann Integration Integration is concerned with the problem of ¯nding the area of a region under a curve. Let us start with a simple problem : Find the area A of the region enclosed by a circle of radius r. For an arbitrary n, consider the n equal inscribed and superscibed triangles as shown in Figure 1. f(x) f(x) π 2 n O a b O a b Figure 1 Figure 2 Since A is between the total areas of the inscribed and superscribed triangles, we have nr2sin(¼=n)cos(¼=n) · A · nr2tan(¼=n): By sandwich theorem, A = ¼r2: We will use this idea to de¯ne and evaluate the area of the region under a graph of a function. Suppose f is a non-negative function de¯ned on the interval [a; b]: We ¯rst subdivide the interval into a ¯nite number of subintervals. Then we squeeze the area of the region under the graph of f between the areas of the inscribed and superscribed rectangles constructed over the subintervals as shown in Figure 2. If the total areas of the inscribed and superscribed rectangles converge to the same limit as we make the partition of [a; b] ¯ner and ¯ner then the area of the region under the graph of f can be de¯ned as this limit and f is said to be integrable. Let us de¯ne whatever has been explained above formally. The Riemann Integral Let [a; b] be a given interval. A partition P of [a; b] is a ¯nite set of points x0; x1; x2; : : : ; xn such that a = x0 · x1 · ¢ ¢ ¢ · xn¡1 · xn = b.
    [Show full text]
  • Bilateral Tempered Fractional Derivatives
    S S symmetry Article Bilateral Tempered Fractional Derivatives Manuel Duarte Ortigueira 1,* and Gabriel Bengochea 2 1 Centre of Technology and Systems-UNINOVA, NOVA School of Science and Technology of NOVA University of Lisbon, Quinta da Torre, 2829-516 Caparica, Portugal 2 Academia de Matemática, Universidad Autónoma de la Ciudad de México, Ciudad de México 04510, Mexico; [email protected] * Correspondence: [email protected] Abstract: The bilateral tempered fractional derivatives are introduced generalising previous works on the one-sided tempered fractional derivatives and the two-sided fractional derivatives. An analysis of the tempered Riesz potential is done and shows that it cannot be considered as a derivative. Keywords: tempered fractional derivative; one-sided tempered fractional derivative; bilateral tem- pered fractional derivative; tempered riesz potential MSC: Primary 26A33; Secondary 34A08; 35R11 1. Introduction In a recent paper [1], we presented a unified formulation for the one-sided Tempered Fractional Calculus, that includes the classic, tempered, substantial, and shifted fractional operators [2–9]. Citation: Ortigueira, M.D.; Here, we continue in the same road by presenting a study on the two-sided tempered Bengochea, G. Bilateral Tempered operators that generalize and include the one-sided. The most interesting is the tempered Fractional Derivatives. Symmetry Riesz potential that was proposed in analogy with the one-sided tempered derivatives [10]. 2021, 13, 823. https://doi.org/ However, a two-sided tempering was introduced before, in the study of the called variance 10.3390/sym13050823 gamma processes [11,12], in Statistical Physics for modelling turbulence, under the concept Academic Editors: Francisco Martínez of truncated Lévy flight [8,13–17], and for defining the Regular Lévy Processes of Expo- González and Mohammed KA Kaabar nential type [2,10,18].
    [Show full text]
  • Hardy-Type Inequalities for Integral Transforms Associated with Jacobi Operator
    HARDY-TYPE INEQUALITIES FOR INTEGRAL TRANSFORMS ASSOCIATED WITH JACOBI OPERATOR M. DZIRI AND L. T. RACHDI Received 8 April 2004 and in revised form 24 December 2004 We establish Hardy-type inequalities for the Riemann-Liouville and Weyl transforms as- sociated with the Jacobi operator by using Hardy-type inequalities for a class of integral operators. 1. Introduction It is well known that the Jacobi second-order differential operator is defined on ]0,+∞[ by 1 d du 2 ∆α,βu(x) = Aα,β(x) + ρ u(x), (1.1) Aα,β(x) dx dx where 2ρ 2α+1 2β+1 (i) Aα,β(x) = 2 sinh (x)cosh (x), (ii) α,β ∈ R; α ≥ β>−1/2, (iii) ρ = α + β +1. The Riemann-Liouville and Weyl transforms associated with Jacobi operator ∆α,β are, respectively, defined, for every nonnegative measurable function f ,by x Rα,β( f )(x) = kα,β(x, y) f (y)dy, 0 ∞ (1.2) Wα,β( f )(y) = kα,β(x, y) f (x)Aα,β(x)dx, y where kα,β is the nonnegative kernel defined, for x>y>0, by −1 2 2−α+3/2Γ(α +1) cosh(2x) − cosh(2y) α / kα,β(x, y) = √ πΓ(α +1/2)coshα+β(x)sinh2α(x) (1.3) 1 cosh(x) − cosh(y) × F α + β,α − β;α + ; 2 2cosh(x) Copyright © 2005 Hindawi Publishing Corporation International Journal of Mathematics and Mathematical Sciences 2005:3 (2005) 329–348 DOI: 10.1155/IJMMS.2005.329 330 Hardy-type inequalities and F is the Gaussian hypergeometric function.
    [Show full text]
  • K-Weyl Fractional Integral I Introduction and Preliminaries
    Int. Journal of Math. Analysis, Vol. 6, 2012, no. 34, 1685 - 1691 k-Weyl Fractional Integral Luis Guillermo Romero, Ruben Alejandro Cerutti and Gustavo Abel Dorrego Faculty of Exact Sciences National University of Nordeste. Avda. Libertad 5540 (3400) Corrientes, Argentina [email protected] [email protected] Abstract In this paper we present a generalization to the k-calculus of the Weyl Fractional Integral. Show the semigroup property and calculate their Fractional Fourier Transform. Mathematics Subject Classification: 26A33, 42A38 Keywords: k-Fractional Calculus. Weyl fractional integral I Introduction and Preliminaries In [1] Diaz and Pariguan has defined new functions called the k-Gamma function and the Pochhammer k-symbol that are generalization of the clas- sical Gamma function and the classical Pochhammer symbol. Later in 2012, Mubeen and Habibullah [11] has introduced the k-fractional integral of the Riemann-Liouville type. The purpose of this paper is introduce a fractional integral operator of Weyl type and study that may be posible to exprese this integral operator as certain convolution with the singular kernel of Riemann- Liouville. The classical Weyl integral operator of order α is defined (cf. [10]) in the form 1 ∞ W αf(u)= (t − u)α−1f(t)dt (I.1) Γ(α) u u ≥ 0, α>0 and f a function belonging to S(R) the Schwartzian space of functions, and Γ(z) is the Gamma Euler function given by the integral 1686 L. G. Romero, R. A. Cerutti and G. A. Dorrego ∞ Γ(z)= e−ttz−1dt, z ∈ C, Re(z) > 0, cf.
    [Show full text]
  • Intuitive Mathematical Discourse About the Complex Path Integral Erik Hanke
    Intuitive mathematical discourse about the complex path integral Erik Hanke To cite this version: Erik Hanke. Intuitive mathematical discourse about the complex path integral. INDRUM 2020, Université de Carthage, Université de Montpellier, Sep 2020, Cyberspace (virtually from Bizerte), Tunisia. hal-03113845 HAL Id: hal-03113845 https://hal.archives-ouvertes.fr/hal-03113845 Submitted on 18 Jan 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Intuitive mathematical discourse about the complex path integral Erik Hanke1 1University of Bremen, Faculty of Mathematics and Computer Science, Germany, [email protected] Interpretations of the complex path integral are presented as a result from a multi-case study on mathematicians’ intuitive understanding of basic notions in complex analysis. The first case shows difficulties of transferring the image of the integral in real analysis as an oriented area to the complex setting, and the second highlights the complex path integral as a tool in complex analysis with formal analogies to path integrals in multivariable calculus. These interpretations are characterised as a type of intuitive mathematical discourse and the examples are analysed from the point of view of substantiation of narratives within the commognitive framework.
    [Show full text]