Quad Ropes: Immutable, Declarative Arrays with Parallelizable Operations
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Traits: Experience with a Language Feature
7UDLWV([SHULHQFHZLWKD/DQJXDJH)HDWXUH (PHUVRQ50XUSK\+LOO $QGUHZ3%ODFN 7KH(YHUJUHHQ6WDWH&ROOHJH 2*,6FKRRORI6FLHQFH1(QJLQHHULQJ$ (YHUJUHHQ3DUNZD\1: 2UHJRQ+HDOWKDQG6FLHQFH8QLYHUVLW\ 2O\PSLD$:$ 1::DONHU5G PXUHPH#HYHUJUHHQHGX %HDYHUWRQ$25 EODFN#FVHRJLHGX ABSTRACT the desired semantics of that method changes, or if a bug is This paper reports our experiences using traits, collections of found, the programmer must track down and fix every copy. By pure methods designed to promote reuse and understandability reusing a method, behavior can be defined and maintained in in object-oriented programs. Traits had previously been used to one place. refactor the Smalltalk collection hierarchy, but only by the crea- tors of traits themselves. This experience report represents the In object-oriented programming, inheritance is the normal way first independent test of these language features. Murphy-Hill of reusing methods—classes inherit methods from other classes. implemented a substantial multi-class data structure called ropes Single inheritance is the most basic and most widespread type of that makes significant use of traits. We found that traits im- inheritance. It allows methods to be shared among classes in an proved understandability and reduced the number of methods elegant and efficient way, but does not always allow for maxi- that needed to be written by 46%. mum reuse. Consider a small example. In Squeak [7], a dialect of Smalltalk, Categories and Subject Descriptors the class &ROOHFWLRQ is the superclass of all the classes that $UUD\ +HDS D.2.3 [Programming Languages]: Coding Tools and Tech- implement collection data structures, including , , 6HW niques - object-oriented programming and . The property of being empty is common to many ob- jects—it simply requires that the object have a size method, and D.3.3 [Programming Languages]: Language Constructs and that the method returns zero. -

The Cedar Programming Environment: a Midterm Report and Examination
The Cedar Programming Environment: A Midterm Report and Examination Warren Teitelman The Cedar Programming Environment: A Midterm Report and Examination Warren Teitelman t CSL-83-11 June 1984 [P83-00012] © Copyright 1984 Xerox Corporation. All rights reserved. CR Categories and Subject Descriptors: D.2_6 [Software Engineering]: Programming environments. Additional Keywords and Phrases: integrated programming environment, experimental programming, display oriented user interface, strongly typed programming language environment, personal computing. t The author's present address is: Sun Microsystems, Inc., 2550 Garcia Avenue, Mountain View, Ca. 94043. The work described here was performed while employed by Xerox Corporation. XEROX Xerox Corporation Palo Alto Research Center 3333 Coyote Hill Road Palo Alto, California 94304 1 Abstract: This collection of papers comprises a report on Cedar, a state-of-the-art programming system. Cedar combines in a single integrated environment: high-quality graphics, a sophisticated editor and document preparation facility, and a variety of tools for the programmer to use in the construction and debugging of his programs. The Cedar Programming Language is a strongly-typed, compiler-oriented language of the Pascal family. What is especially interesting about the Ce~ar project is that it is one of the few examples where an interactive, experimental programming environment has been built for this kind of language. In the past, such environments have been confined to dynamically typed languages like Lisp and Smalltalk. The first paper, "The Roots of Cedar," describes the conditions in 1978 in the Xerox Palo Alto Research Center's Computer Science Laboratory that led us to embark on the Cedar project and helped to define its objectives and goals. -

Smalltalk Idioms
Smalltalk Idioms Farewell and a wood pile Kent Beck IT’S THE OBJECTS, STUPID If we parsed the string “@years”, the resulting picture S me awhile to see the obvious. Some- would look like Figure 6. When the BinaryFunction un- times even longer than that. Three or four times in the wraps its children, the right function will be in place. last month I’ve been confronted by problems I had a As I said, several times in the last month I’ve faced hard time solving. In each case, the answer became clear baffling problems that became easy when I asked myself when I asked myself the simple question, “How can I the question, “How could I make an object to solve this make an object to solve this problem for me?” You think problem for me?” Sometimes it was a method that just I’d have figured it out by now: got a problem? make an didn’t want to be simplified, so I created an object just for object for it. that method. Sometimes it was a question of adding Here’s an example: I had to write an editor for a tree features to an object for a particular purpose without clut- structure. There were several ways of viewing and editing tering the object (as in the editing example). I recommend the tree. On the left was a hierarchical list. On the top right that the next time you run into a problem that just doesn’t was a text editor on the currently selected node of the tree. -

Effective STL
Effective STL Author: Scott Meyers E-version is made by: Strangecat@epubcn Thanks is given to j1foo@epubcn, who has helped to revise this e-book. Content Containers........................................................................................1 Item 1. Choose your containers with care........................................................... 1 Item 2. Beware the illusion of container-independent code................................ 4 Item 3. Make copying cheap and correct for objects in containers..................... 9 Item 4. Call empty instead of checking size() against zero. ............................. 11 Item 5. Prefer range member functions to their single-element counterparts... 12 Item 6. Be alert for C++'s most vexing parse................................................... 20 Item 7. When using containers of newed pointers, remember to delete the pointers before the container is destroyed. ........................................................... 22 Item 8. Never create containers of auto_ptrs. ................................................... 27 Item 9. Choose carefully among erasing options.............................................. 29 Item 10. Be aware of allocator conventions and restrictions. ......................... 34 Item 11. Understand the legitimate uses of custom allocators........................ 40 Item 12. Have realistic expectations about the thread safety of STL containers. 43 vector and string............................................................................48 Item 13. Prefer vector -

The Ocaml System Release 4.02
The OCaml system release 4.02 Documentation and user's manual Xavier Leroy, Damien Doligez, Alain Frisch, Jacques Garrigue, Didier R´emy and J´er^omeVouillon August 29, 2014 Copyright © 2014 Institut National de Recherche en Informatique et en Automatique 2 Contents I An introduction to OCaml 11 1 The core language 13 1.1 Basics . 13 1.2 Data types . 14 1.3 Functions as values . 15 1.4 Records and variants . 16 1.5 Imperative features . 18 1.6 Exceptions . 20 1.7 Symbolic processing of expressions . 21 1.8 Pretty-printing and parsing . 22 1.9 Standalone OCaml programs . 23 2 The module system 25 2.1 Structures . 25 2.2 Signatures . 26 2.3 Functors . 27 2.4 Functors and type abstraction . 29 2.5 Modules and separate compilation . 31 3 Objects in OCaml 33 3.1 Classes and objects . 33 3.2 Immediate objects . 36 3.3 Reference to self . 37 3.4 Initializers . 38 3.5 Virtual methods . 38 3.6 Private methods . 40 3.7 Class interfaces . 42 3.8 Inheritance . 43 3.9 Multiple inheritance . 44 3.10 Parameterized classes . 44 3.11 Polymorphic methods . 47 3.12 Using coercions . 50 3.13 Functional objects . 54 3.14 Cloning objects . 55 3.15 Recursive classes . 58 1 2 3.16 Binary methods . 58 3.17 Friends . 60 4 Labels and variants 63 4.1 Labels . 63 4.2 Polymorphic variants . 69 5 Advanced examples with classes and modules 73 5.1 Extended example: bank accounts . 73 5.2 Simple modules as classes . -

Thinking in C++ 2Nd Edition Volume 2
Thinking in C++ 2nd edition Volume 2: Standard Libraries & Advanced Topics To be informed of future releases of this document and other information about object- oriented books, documents, seminars and CDs, subscribe to my free newsletter. Just send any email to: [email protected] ________________________________________________________________________ “This book is a tremendous achievement. You owe it to yourself to have a copy on your shelf. The chapter on iostreams is the most comprehensive and understandable treatment of that subject I’ve seen to date.” Al Stevens Contributing Editor, Doctor Dobbs Journal “Eckel’s book is the only one to so clearly explain how to rethink program construction for object orientation. That the book is also an excellent tutorial on the ins and outs of C++ is an added bonus.” Andrew Binstock Editor, Unix Review “Bruce continues to amaze me with his insight into C++, and Thinking in C++ is his best collection of ideas yet. If you want clear answers to difficult questions about C++, buy this outstanding book.” Gary Entsminger Author, The Tao of Objects “Thinking in C++ patiently and methodically explores the issues of when and how to use inlines, references, operator overloading, inheritance and dynamic objects, as well as advanced topics such as the proper use of templates, exceptions and multiple inheritance. The entire effort is woven in a fabric that includes Eckel’s own philosophy of object and program design. A must for every C++ developer’s bookshelf, Thinking in C++ is the one C++ book you must have if you’re doing serious development with C++.” Richard Hale Shaw Contributing Editor, PC Magazine Thinking In C++ 2nd Edition, Volume 2 Bruce Eckel President, MindView Inc. -

Mergeable Replicated Data Types
Mergeable Replicated Data Types GOWTHAM KAKI, Purdue University, USA SWARN PRIYA, Purdue University, USA KC SIVARAMAKRISHNAN, IIT Madras, India 154 SURESH JAGANNATHAN, Purdue University, USA Programming geo-replicated distributed systems is challenging given the complexity of reasoning about different evolving states on different replicas. Existing approaches to this problem impose significant burden on application developers to consider the effect of how operations performed on one replica are witnessed and applied on others. To alleviate these challenges, we present a fundamentally different approach to programming in the presence of replicated state. Our insight is based on the use of invertible relational specifications of an inductively-defined data type as a mechanism to capture salient aspects of the data type relevantto how its different instances can be safely merged in a replicated environment. Importantly, because these specifications only address a data type’s (static) structural properties, their formulation does not require exposing low-level system-level details concerning asynchrony, replication, visibility, etc. As a consequence, our framework enables the correct-by-construction synthesis of rich merge functions over arbitrarily complex (i.e., composable) data types. We show that the use of a rich relational specification language allows us to extract sufficient conditions to automatically derive merge functions that have meaningful non-trivial convergence properties. We incorporate these ideas in a tool called Quark, and demonstrate its utility via a detailed evaluation study on real-world benchmarks. CCS Concepts: • Computing methodologies → Distributed programming languages; • Computer systems organization → Availability; • Software and its engineering → Formal software verification. Additional Key Words and Phrases: Replication, Weak Consistency, CRDTs, Git, Version Control ACM Reference Format: Gowtham Kaki, Swarn Priya, KC Sivaramakrishnan, and Suresh Jagannathan. -

Fast Longest Prefix Matching: Algorithms, Analysis, and Applications
Diss. ETH No. 13266 Fast Longest Prefix Matching: Algorithms, Analysis, and Applications A dissertation submitted to the SWISS FEDERAL INSTITUTE OF TECHNOLOGY ZURICH for the degree of DOCTOR OF TECHNICAL SCIENCES presented by MARCEL WALDVOGEL Dipl. Informatik-Ing. ETH born August 28, 1968 citizen of Switzerland accepted on the recommendation of Prof. Dr. B. Plattner, examiner Prof. Dr. G. Varghese, co-examiner 2000 In memoriam Ulrich Breuer An ingenious mind in a physical world Abstract Many current problems demand efficient best matching algorithms. Network devices alone show several applications. They need to determine a longest matching prefix for packet routing or establishment of virtual circuits. In inte- grated services packet networks, packets need to be classified by trying to find the most specific match from a large number of patterns, each possibly con- taining wildcards at arbitrary positions. Other areas of applications include such diverse areas as geographical information systems (GIS) and persistent databases. We describe a class of best matching algorithms based on slicing perpen- dicular to the patterns and performing a modified binary search over these slices. We also analyze their complexity and performance. We then introduce schemes that allow the algorithm to “learn” the structure of the database and adapt itself to it. Furthermore, we show how to efficiently implement our al- gorithm both using general-purpose hardware and using software running on popular personal computers and workstations. The research presented herein was originally driven by current demands in the Internet. Since the advent of the World Wide Web, the number of users, hosts, domains, and networks connected to the Internet seems to be explod- ing. -

Ondrej B´Ilka Pattern Matching in Compilers
Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Ondˇrej B´ılka Pattern matching in compilers arXiv:1210.3593v1 [cs.PL] 12 Oct 2012 Department of applied mathematics Supervisor of the master thesis: Jan Hubiˇcka Study programme: Diskr´etn´ımodely a algoritmy Specialization: Diskr´etn´ımodely a algoritmy Prague 2012 Acknowledgements I would like to thank to everybody at Charles University who made this possible. I would like to thank Pavel Klav´ıkfor help with the typography. I would like to thank Andrew Goodall for a help with traps of the English gram- mar. I would like to thank my advisor Honza Hubiˇcka for help, time, endurance, valu- able comments and insights how compilers work in real world. I would like to thank to many authors on whose work is this thesis built. I would like to thank my family for their love. I declare that I carried out this master thesis independently, and only with the cited sources, literature and other professional sources. I understand that my work relates to the rights and obligations under the Act No. 121/2000 Coll., the Copyright Act, as amended, in particular the fact that the Charles University in Prague has the right to conclude a license agreement on the use of this work as a school work pursuant to Section 60 paragraph 1 of the Copyright Act. In ........ date ............ signature of the author N´azev pr´ace: Pattern matching in compilers Autor: Ondˇrej B´ılka Katedra: Katedra Aplikovan´eMatematiky Vedouc´ıdiplomov´epr´ace: Jan Hubiˇcka, Katedra Aplikovan´e Matematiky Abstrakt: V t´eto pr´aci vyvineme n´astroje na efektivn´ıa flexibiln´ıpattern match- ing. -
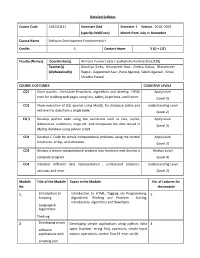
Detailed Syllabus Course Code 15B11CI111 Semester
Detailed Syllabus Course Code 15B11CI111 Semester Odd Semester I. Session 2018 -2019 (specify Odd/Even) Month from July to December Course Name Software Development Fundamentals-I Credits 4 Contact Hours 3 (L) + 1(T) Faculty (Names) Coordinator(s) Archana Purwar ( J62) + Sudhanshu Kulshrestha (J128) Teacher(s) Adwitiya Sinha, Amanpreet Kaur, Chetna Dabas, Dharamveer (Alphabetically) Rajput, Gaganmeet Kaur, Parul Agarwal, Sakshi Agarwal , Sonal, Shradha Porwal COURSE OUTCOMES COGNITIVE LEVELS CO1 Solve puzzles , formulate flowcharts, algorithms and develop HTML Apply Level code for building web pages using lists, tables, hyperlinks, and frames (Level 3) CO2 Show execution of SQL queries using MySQL for database tables and Understanding Level retrieve the data from a single table. (Level 2) CO 3 Develop python code using the constructs such as lists, tuples, Apply Level dictionaries, conditions, loops etc. and manipulate the data stored in (Level 3) MySQL database using python script. CO4 Develop C Code for simple computational problems using the control Apply Level structures, arrays, and structure. (Level 3) CO5 Analyze a simple computational problem into functions and develop a Analyze Level complete program. (Level 4) CO6 Interpret different data representation , understand precision, Understanding Level accuracy and error (Level 2) Module Title of the Module Topics in the Module No. of Lectures for No. the module 1. Introduction to Introduction to HTML, Tagging v/s Programming, 5 Scripting Algorithmic Thinking and Problem Solving, Introductory algorithms and flowcharts Language & Algorithmic Thinking 2. Developing simple Developing simple applications using python; data 4 software types (number, string, list), operators, simple input applications with output, operations, control flow (if -else, while) scripting and visual languages 3. -

The Quadtree and Related Hierarchical Data Structures
The Quadtree and Related Hierarchical Data Structures HANAN SAMET Computer Sdence Department, University of Maryland, College Park, Maryland 20742 A tutorial survey is presented of the quadtree and related hierarchical data structures. They are based on the principle of recursive decomposition. The emphasis is on the representation of data used in applications in image processing, computer graphics, geographic information systems, and robotics. There is a greater emphasis on region data (i.e., two-dimensional shapes) and to a lesser extent on point, curvilinear, and three dimensional data. A number of operations in which such data structures find use are examined in greater detail. Categories and Subject Descriptors: E.1 [Data]: Data Structures-trees; H.3.2 [Information Storage and Retrieval]: Information Storage-file organization; 1.2.1 [Artificial Intelligence]: Applications and Expert Systems-cartography; 1.2.10 [Artificial Intelligence): Vision and Scene Understanding-representations, data structures, and transforms; 1.3.3 [Computer Graphics]: Picture/Image Generation display algorithms; viewing algorithms; 1.3.5 [Computer Graphics]: Computational Geometry and Object Modeling-curve, surface, solid, and object representations; geometric algorithms, languages, and systems; l.4.2 [Image Processing]: Compression (Coding)-approximate methods; exact coding; 1.4. 7 [Image Processing]: Feature Measurement-moments; projections; size and shape; J.6 [Computer-Aided Engineering]: Computer-Aided Design (CAD) General Terms: Algorithms Additional -

Camomile : a Unicode Library for Ocaml
Camomile : A Unicode library for OCaml Yoriyuki Yamagata National Institute of Advanced Science and Technology (AIST) ML Workshop, September 18, 2011 Outline Overview ASCII to Unicode : A challenge of multilingualization A brief tour of Camomile modules ulib Conclusion Outline Overview ASCII to Unicode : A challenge of multilingualization A brief tour of Camomile modules ulib Conclusion I Unicode character type I UTF-8, UTF-16, UTF-32 strings I Conversion to/from approx 200 encodings I Case mapping I Collation (sort and search) Camomile - A Unicode library for OCaml Overview - functionality I Unicode character type I UTF-8, UTF-16, UTF-32 strings I Conversion to/from approx 200 encodings I Case mapping I Collation (sort and search) Overview - functionality Camomile - A Unicode library for OCaml I UTF-8, UTF-16, UTF-32 strings I Conversion to/from approx 200 encodings I Case mapping I Collation (sort and search) Overview - functionality Camomile - A Unicode library for OCaml I Unicode character type I Conversion to/from approx 200 encodings I Case mapping I Collation (sort and search) Overview - functionality Camomile - A Unicode library for OCaml I Unicode character type I UTF-8, UTF-16, UTF-32 strings I Case mapping I Collation (sort and search) Overview - functionality Camomile - A Unicode library for OCaml I Unicode character type I UTF-8, UTF-16, UTF-32 strings I Conversion to/from approx 200 encodings I Collation (sort and search) Overview - functionality Camomile - A Unicode library for OCaml I Unicode character type I UTF-8, UTF-16,